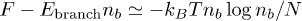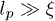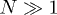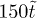Abstract
We study the dynamics of concentrated, long, semi-flexible, unknotted and unlinked ring polymers embedded in a gel by Monte Carlo simulation of a coarse-grained model. This involves the ansatz that the rings compactify into a duplex structure where they can be modelled as linear polymers. The classical polymer glass transition involves a rapid loss of microscopic freedom within the polymer molecule as the temperature is reduced toward Tg. Here we are interested in temperatures well above Tg where the polymers retain high microscopic mobility. We analyse the slowing of stress relaxation originating from inter-ring penetrations (threadings). For long polymers an extended network of quasi-topological penetrations forms. The longest relaxation time appears to depend exponentially on the ring polymer contour length, reminiscent of the usual exponential slowing (e.g., with temperature) in classical glasses. Finally, we discuss how this represents a universality class for glassy dynamics.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 3.0 License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
While a great deal of work continues to be published on the glass transition, e.g., in colloids [1–3] and polymers [4–6], a complete understanding of the transition remains elusive. It is generally associated with the suppression of molecular motion due to jamming and/or cooling where, as a result, the system can take an extremely long time to reach equilibrium. The glass transition has several characteristic properties, including a dramatic (exponential) slowing of dynamics as the temperature is reduced towards a glass transition temperature Tg, combined with the lack of any crystalline order or the thermodynamic signatures of a true phase transition. Beyond these broad features the glass transition appears to lack universality in the sense that its properties depend on the microscopic details of each system. There have been recent attempts to understand this transition in terms of the pinning of a fraction of components [7], which has close analogies with the work we outline below.
In the present work we investigate a simplified theoretical model of the diffusive dynamics of high-molecular-weight ring polymers, above the overlap concentration 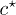 , embedded in a polymer gel. This would correspond to the same experimental system as would be employed for gel electrophoresis of circular plasmid DNA (here without the applied field) [8–11]; DNA electrophoresis is one of the core techniques of molecular biology [12,13]. There is evidence that open circular (ring) DNA can be "trapped" in agarose gel, with exponential slowing-down of its migration. This phenomenon is attributed to the presence of protruding gel fibres, that thread through the ring-shaped DNA [14]. We neglect such ends protruding from the gel in what follows but argue that similar penetrations can occur between two ring polymers when one threads through the other. If these penetrations are numerous, then they may dramatically slow the diffusion of rings. It is this effect that we are most interested in investigating. A few authors have previously conjectured that such interpenetration of rings may occur and that this might significantly slow the dynamics [15,16]. However, no quantitative theory has previously been proposed.
, embedded in a polymer gel. This would correspond to the same experimental system as would be employed for gel electrophoresis of circular plasmid DNA (here without the applied field) [8–11]; DNA electrophoresis is one of the core techniques of molecular biology [12,13]. There is evidence that open circular (ring) DNA can be "trapped" in agarose gel, with exponential slowing-down of its migration. This phenomenon is attributed to the presence of protruding gel fibres, that thread through the ring-shaped DNA [14]. We neglect such ends protruding from the gel in what follows but argue that similar penetrations can occur between two ring polymers when one threads through the other. If these penetrations are numerous, then they may dramatically slow the diffusion of rings. It is this effect that we are most interested in investigating. A few authors have previously conjectured that such interpenetration of rings may occur and that this might significantly slow the dynamics [15,16]. However, no quantitative theory has previously been proposed.
It is also possible to synthesise non-DNA ring polymers with few knots and concatenations [17,18]. Their rheological properties are now thought to be rather sensitive to contamination from linear polymers [19,20] and, to a lesser extent, polydispersity. It is also challenging to measure the rheology associated with the extreme (long-lived) tail of the stress relaxation in these systems, this being the regime of most interest to us here.
There is now a significant body of literature on ring polymers, their static properties [21–24] and conformations in the entangled state [25–27]. Few formal theoretical results exist due to the difficulty in handling the essential non-locality of the topological constraints. A number of simulation studies have been performed on highly concentrated rings (ring melts) [23–26], a somewhat different system to that in which we are interested in here. Here, there are hints that the chains may approach a fully compact globular conformation in the long-chain limit. In this case the scaling of the polymer radius of gyration with the degree of polymerisation  would approach an exponent of exactly
would approach an exponent of exactly 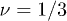 , although this remains unproven. As usual, computational simulations involve inherent limits on the polymer contour length L, and the total number of polymer chains Nc. They are further hindered by the fact that the entanglement length le (the average contour length of chain between effective entanglements) can be
, although this remains unproven. As usual, computational simulations involve inherent limits on the polymer contour length L, and the total number of polymer chains Nc. They are further hindered by the fact that the entanglement length le (the average contour length of chain between effective entanglements) can be 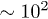 monomeric units, or even more [23,28]. Computer simulations that explicitly include realistic monomeric units are therefore effectively handicapped by two orders of magnitude in polymer size, due to the value of le, and hence at least six orders of magnitude in time, assuming the dynamics are no slower than reptative [29].
monomeric units, or even more [23,28]. Computer simulations that explicitly include realistic monomeric units are therefore effectively handicapped by two orders of magnitude in polymer size, due to the value of le, and hence at least six orders of magnitude in time, assuming the dynamics are no slower than reptative [29].
Our approach involves several simplifying assumptions that mitigate this problem. Firstly we adopt the ansatz that the ring polymer compactifies in such a way as to form a duplex structure in which each segment of the "tube" of entanglements that confines it [29] contains an outgoing and a returning segment of the ring polymer. This is a result of the rings not being able to cross through the gel polymer [16,21,27]. We further assume that this compact, duplex structure is linear, see fig. 1. This state is quite different from the fully compact globule with 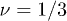 , having an exponent closer to the random walk value
, having an exponent closer to the random walk value 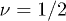 although this value is moot given the way in which we will later treat space. The effective length of the tube is reduced by roughly a factor of two but such a chain is now guaranteed to satisfy its topological constraints and to remain unknotted and unlinked, the form in which it is assumed to have been synthesised.
although this value is moot given the way in which we will later treat space. The effective length of the tube is reduced by roughly a factor of two but such a chain is now guaranteed to satisfy its topological constraints and to remain unknotted and unlinked, the form in which it is assumed to have been synthesised.
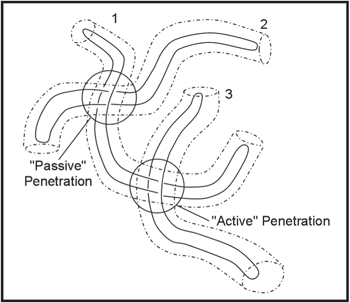
Fig. 1. A schematic diagram showing three unbranched compactified ring polymers (solid curves) and the tubes (dash-dotted curves) provided by their entanglements with a background gel and/or neighbouring rings (not shown). The labels identify the nature of penetrations on polymer 1. Here polymer 2 has actively penetrated polymer 1, creating an associated passive penetration in the corresponding tube segment of polymer 1. Polymer 3 has been penetrated by polymer 1, resulting in a passive penetration to chain 3 and an active penetration to chain 1. The passive penetration on polymer 1 will remain until one end of polymer 2 has diffused through that tube segment. Until that happens, the motion of polymer 1 is restricted by this penetration, which prevents either end diffusing through the associated tube segment. The active penetration on polymer 1 will be lost as soon as either of its ends moves through the tube segment containing this penetration, simultaneously annihilating the corresponding passive penetration on polymer 3.
Download figure:
Standard imageThese linear duplex states represent an explicit set of microscopic configurations that rigorously satisfy all topological constraints. Branching of this duplex structure involves a free-energy penalty if the persistence length of the chain lp is much greater than the mesh size of the background gel ξ (see footnote 1). Here we aim to study the effect of inter-ring penetrations perturbatively, where they remain rare (as a fraction of all tube segments). It is possible that the character of the glass-like slowing-down that we analyse below will change if there is branching of the duplex structure. Nonetheless, the role of topological constraints arising from penetrations has not been explored before and the non-branched case would seem the natural starting point. We speculate that the existence of the glass-like behaviour would not be lost in the presence of branching, provided that the ring polymers have sufficient interpenetrations.
A novel aspect of our approach is the way in which we account for penetration events, see fig. 1. These do not violate the overall topological constraints and can be thought of as a perturbative relaxation of the compact chain ansatz introduced above. The free energy (or statistical weight) associated with these penetration events is difficult to calculate a priori and depends on the monomer density, the persistence length lp and other microscopic-level details of the physics employed, e.g., the inter-monomer interaction potential(s). We do not attempt to compute this from first principles but rather define a parameter p to be the probability that the duplex chain's primitive path, the average trajectory of the duplex chain within the tube of entanglements that confines it [29], penetrates a neighbouring ring on diffusing one entanglement length along the tube, roughly the Boltzmann factor associated with the free energy of penetration. Provided p is non-zero we may have many penetrations in the large N limit. As we will show below, the onset of the glass-like transition occurs when the number of penetrations per ring is only of order unity.
Secondly, we coarse-grain the polymer on the scale of the entanglement length le. Thus, in what follows, N represents the number of entanglement lengths along the duplex ring polymer, rather than the molecular degree of polymerisation itself. We then study the curvilinear diffusion of the primitive chain of the polymer within the tube formed by the confinements provided by the fixed obstacles [29] via a Monte Carlo (MC) algorithm. In this way one unit of simulation time  is the "hop" time taken for each duplex polymer to diffuse a mean squared distance of unity (in units where
is the "hop" time taken for each duplex polymer to diffuse a mean squared distance of unity (in units where  ). Here it might be helpful to think of the curvilinear coordinates for each chain being projected onto a straight line so that each chain can be thought of as moving one unit to the right or left, at random, per time step. The stress relaxation is therefore proportional to the function G(t), corresponding to the fraction of original (stressed) tube segments remaining after time t, as usual [29]. In the absence of any penetrations this algorithm correctly approximates the Doi-Edwards expression for stress relation [29], with a single characteristic stress relaxation time scale
). Here it might be helpful to think of the curvilinear coordinates for each chain being projected onto a straight line so that each chain can be thought of as moving one unit to the right or left, at random, per time step. The stress relaxation is therefore proportional to the function G(t), corresponding to the fraction of original (stressed) tube segments remaining after time t, as usual [29]. In the absence of any penetrations this algorithm correctly approximates the Doi-Edwards expression for stress relation [29], with a single characteristic stress relaxation time scale 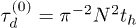 . Here and in what follows, we work in units of time in which
. Here and in what follows, we work in units of time in which  with
with  the curvilinear diffusion constant, ζ a microscopic friction constant and kBT the thermal energy.
the curvilinear diffusion constant, ζ a microscopic friction constant and kBT the thermal energy.
Fig. 2. (Colour on-line) A diagram showing how our Monte Carlo simulation operates. Panels (a)–(c) represent states of the system at different times, starting with the state shown in fig. 1(a). The rings are labelled as in fig. 1, with passive penetrations (red dot) and active penetrations (blue ring) existing in pairs, indicated by connecting lines. Each "hop" time step  every ring attempts to move, at random, one entanglement length along their primitive path, here projected to either left or right in a way that is analogous to the curvilinear diffusion of classical reptation [29]. The ticks on the axes represent these entanglement lengths. Thus, after a few time steps, the rings have moved from the state shown in (a) to (b). Each time a ring moves there is a probability p that it penetrates another at random. This has just happened in (b), where the new active penetration on the leading end of chain 3 is associated with its passive penetration of chain 2. A few time steps later, the systems finds itself in state (c). Chain 2 has just moved to the right, annihilating the trailing active penetration associated with its passive penetration of chain 1. Chain 3 attempts a further move to the right. This move is rejected due to the presence of passive penetration in its trailing segment. The emergence of a glassy state can ultimately be traced to the proliferation of such rejections (penetrations).
every ring attempts to move, at random, one entanglement length along their primitive path, here projected to either left or right in a way that is analogous to the curvilinear diffusion of classical reptation [29]. The ticks on the axes represent these entanglement lengths. Thus, after a few time steps, the rings have moved from the state shown in (a) to (b). Each time a ring moves there is a probability p that it penetrates another at random. This has just happened in (b), where the new active penetration on the leading end of chain 3 is associated with its passive penetration of chain 2. A few time steps later, the systems finds itself in state (c). Chain 2 has just moved to the right, annihilating the trailing active penetration associated with its passive penetration of chain 1. Chain 3 attempts a further move to the right. This move is rejected due to the presence of passive penetration in its trailing segment. The emergence of a glassy state can ultimately be traced to the proliferation of such rejections (penetrations).
Download figure:
Standard imageOur algorithm includes the effects of ring penetration events as follows: We introduce Nc overlapping polymer chains into the system. These all start in the unpenetrated state. Each time step a randomly chosen polymer attempts to move rightward or leftward by one unit of length. This move is allowed, and the location of the polymer is updated via an appropriate translation, provided the chain does not contain a passive penetration in the last (trailing) segment, preventing this move, see fig. 2. If this occurs, the move fails, as shown in fig. 2(c). Thus, we neglect tube length fluctuations throughout2. Each sweep of Nc such moves corresponds to a physical hop time 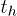 . Every polymer that successfully moves i) experiences a corresponding reverse translation of all active and passive penetrations, these being associated with the corresponding tube segments, rather than the polymer itself (in our code, as in the physical system, these penetrations remain stationary and only the polymer position is updated), see fig. 2(a); ii) if an active penetration was associated with its trailing tube segment, this is annihilated, together with the corresponding passive penetration through a tube segment on another polymer, see fig. 2(c); iii) a new active-passive penetration pair is created with the probability p, see fig. 2(b). In this case the active penetration is associated with the newly created leading tube segment on the moving chain, the corresponding passive penetration is associated with a randomly chosen tube segment on one of the Nc polymers, unless the segment has already been penetrated or it is the chain leading segment itself. This leads to an initial increase in the number of penetration pairs (from zero) and a slowing of stress relaxation due to the constraints on the polymer dynamics associated with passive penetrations, see fig. 3. Active penetrations themselves do not hinder motion. The stress relaxation function G(t) is obtained by monitoring the remaining length of the original (stressed) tube of each chain3.
. Every polymer that successfully moves i) experiences a corresponding reverse translation of all active and passive penetrations, these being associated with the corresponding tube segments, rather than the polymer itself (in our code, as in the physical system, these penetrations remain stationary and only the polymer position is updated), see fig. 2(a); ii) if an active penetration was associated with its trailing tube segment, this is annihilated, together with the corresponding passive penetration through a tube segment on another polymer, see fig. 2(c); iii) a new active-passive penetration pair is created with the probability p, see fig. 2(b). In this case the active penetration is associated with the newly created leading tube segment on the moving chain, the corresponding passive penetration is associated with a randomly chosen tube segment on one of the Nc polymers, unless the segment has already been penetrated or it is the chain leading segment itself. This leads to an initial increase in the number of penetration pairs (from zero) and a slowing of stress relaxation due to the constraints on the polymer dynamics associated with passive penetrations, see fig. 3. Active penetrations themselves do not hinder motion. The stress relaxation function G(t) is obtained by monitoring the remaining length of the original (stressed) tube of each chain3.
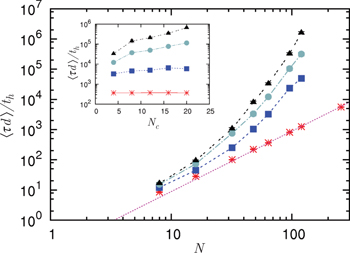
Fig. 3. (Colour on-line). Penetrations significantly slow ring polymer relaxation. The mean stress relaxation (disengagement) time 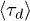 for a system containing
for a system containing 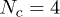 ring polymers depends on their size N and on the penetration parameter p: Shown is data for p = 0 (asterisks), 0.1 (squares), 0.2 (circles) and 0.3 (triangles). The Doi-Edwards' result
ring polymers depends on their size N and on the penetration parameter p: Shown is data for p = 0 (asterisks), 0.1 (squares), 0.2 (circles) and 0.3 (triangles). The Doi-Edwards' result 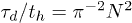 for linear polymers is shown as a (red) dotted straight line, the lines connecting the data points are guides to the eye. Error bars are shown but are often invisibly small. The inset shows that, with N = 64, the mean stress relaxation time
for linear polymers is shown as a (red) dotted straight line, the lines connecting the data points are guides to the eye. Error bars are shown but are often invisibly small. The inset shows that, with N = 64, the mean stress relaxation time 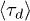 increases with the number of rings Nc available to interpenetrate, except for the red points (p = 0) where there are no penetrations.
increases with the number of rings Nc available to interpenetrate, except for the red points (p = 0) where there are no penetrations.
Download figure:
Standard imageIn our algorithm all rings are available to interpenetrate with all the others, i.e., their coil volumes are assumed to fully overlap. The maximum number Nc for which this is appropriate will therefore be limited by the actual chain number density and coil size in any real system. We find that the system size, here Nc, can strongly control the stress relaxation time, see the inset of fig. 3, noting the log scale. We would explain this as follows: Since the penetration dynamics is always time reversible, there is at least one way to disentangle a system of penetrating rings. Such routes to stress relaxation may be easily accessible if there are few rings. However, if they are numerous (and heavily interpenetrating) they can be obscure and only rarely accessed by chance.
Fig. 4. (Colour on-line). The mean number of penetrations 〈m〉, normalised by the number of tube segments on each polymer N, depends on the penetration probability p, for N = 16 (blue circles) and 32 (green squares). The number of chains 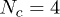 in these simulations. A crude mean-field prediction (solid line) is in qualitative agreement with the simulations, as discussed in the text.
in these simulations. A crude mean-field prediction (solid line) is in qualitative agreement with the simulations, as discussed in the text.
Download figure:
Standard imageThe mean number of penetration per ring 〈m〉 is controlled by p, see fig. 4. A mean-field estimate of this can be constructed as follows. The number of active penetrations (per ring) ma increases by one i) whenever a polymer successfully diffuses, which occurs with probability 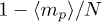 , ii) successfully attempts to create a penetration, which occurs with probability p and iii) attempts to introduce this somewhere not already occupied by a penetration, which occurs with probability
, ii) successfully attempts to create a penetration, which occurs with probability p and iii) attempts to introduce this somewhere not already occupied by a penetration, which occurs with probability 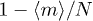 . Similarly an active penetration is lost whenever a chain diffuses through it, which occurs with probability
. Similarly an active penetration is lost whenever a chain diffuses through it, which occurs with probability 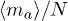 . Hence
. Hence

Finally  which yields an equation for the steady state with a physical root,
which yields an equation for the steady state with a physical root,
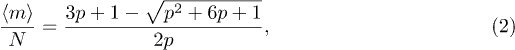
This is compared with the simulation results in fig. 4. A non-uniform spatio-temporal distribution of penetrations is not captured by eq. (1) and this may be the cause of the numerical discrepancy seen in fig. 4.
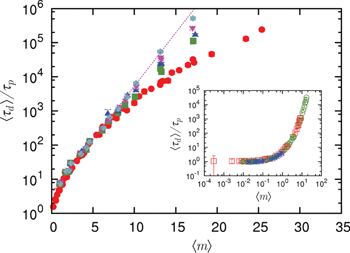
Fig. 5. (Colour on-line). The mean stress relaxation (reptation) time 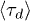 , normalised by the mean time that a chain end encounters a penetration
, normalised by the mean time that a chain end encounters a penetration 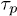 , increases with the mean number of penetrations 〈m〉, itself controlled by p, and with the number of rings Nc available to interpenetrate: shown is data for
, increases with the mean number of penetrations 〈m〉, itself controlled by p, and with the number of rings Nc available to interpenetrate: shown is data for 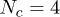 (red circles), 8 (green squares), 12 (dark blue triangles), 16 (purple reversed triangles) and 20 (light blue diamonds). For the largest values of Nc the relaxation is suggestive of an exponential (dotted line) slowing-down with the number of penetrations per ring. The inset shows that the same normalised relaxation time starts to increase sharply above O(1) penetrations per chain; here
(red circles), 8 (green squares), 12 (dark blue triangles), 16 (purple reversed triangles) and 20 (light blue diamonds). For the largest values of Nc the relaxation is suggestive of an exponential (dotted line) slowing-down with the number of penetrations per ring. The inset shows that the same normalised relaxation time starts to increase sharply above O(1) penetrations per chain; here 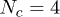 with N = 16 (green open circles) and N = 32 (red open squares) and
with N = 16 (green open circles) and N = 32 (red open squares) and 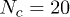 with N = 64 (blue asterisks).
with N = 64 (blue asterisks).
Download figure:
Standard imageWe now examine the variation of relaxation time with the mean number of penetration per ring 〈m〉, rather than the rescaled ring length N, see fig 5. Explicit N-dependence is removed by rescaling the relaxation time by the mean time to diffuse the mean squared distance between penetrations,

where 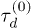 is the Doi-Edwards relaxation time for unpenetrated chains, as before. A dramatic increase in the relaxation time with the number of penetrations is observed, consistent with an exponential rise in the largest systems, see fig. 5. The emergence of exponential slowing down of chain dynamics, and hence stress relaxation, due to the effects of topological constraints is a primary result of the present work. This glass-like behaviour occurs when the average number of penetrations per chain 〈m〉 is at least of order unity. Above this threshold a network of the penetrations starts to form which must be disentangled for stress to fully relax.
is the Doi-Edwards relaxation time for unpenetrated chains, as before. A dramatic increase in the relaxation time with the number of penetrations is observed, consistent with an exponential rise in the largest systems, see fig. 5. The emergence of exponential slowing down of chain dynamics, and hence stress relaxation, due to the effects of topological constraints is a primary result of the present work. This glass-like behaviour occurs when the average number of penetrations per chain 〈m〉 is at least of order unity. Above this threshold a network of the penetrations starts to form which must be disentangled for stress to fully relax.
We believe that our model of quasi-topological entanglements in ring polymers defines a universality class for a glassy dynamics. It is universal in the usual sense that all scaling results are insensitive to i) the precise chemistry of the polymers, provided they are long enough to contain many entanglements, ii) the temperature, provided it is above (the classical) Tg and iii) the concentration, provided it is well above the overlap density in the gel. In such a regime we have shown that our model of compactified ring polymers can be coarse-grained and analysed by including the role of inter-loop penetrations into classical reptative diffusion, which is already well known to be similarly universal [29].
Our model involves a number of simplifying assumptions. It includes space only in the sense that the individual polymers move relative to a tube that is implicitly embedded in space. It is also zero-dimensional, insofar as all chains are assumed to overlap with each other. A more thorough treatment would include spatial effects so that each chain can interpenetrate only with those neighbours with which its coil volume overlaps. It may be that these "clusters" can then form a spatially percolating network of penetrations, leading to true system-size–dependent relaxation times. We have also assumed that the rings reside in a background gel. Finally, our most restrictive assumption is probably that the polymer conformations remain perturbatively close to a fully compactified, linear duplex chain. We believe that this represents a sensible starting point for quantitative analysis and, as discussed above, it seems consistent with the limit 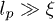 . The assumption that the chains compactify to a linear structure may be harder to justify in the melt (or concentrated solution).
. The assumption that the chains compactify to a linear structure may be harder to justify in the melt (or concentrated solution).
Acknowledgments
We thank George Rowlands and Robin Ball (Warwick) and Andrew Turberfield (Oxford) for assistance and discussion in this millennium and David Weitz (Harvard) and Jan Karlseder (Salk Institute) for those in the last. MST acknowledges the support of a UK EPSRC Leadership Fellowship No. P/E501311/1.
Footnotes
- 1
An extremely crude estimate of the number of branches nb can then be obtained by considering the free energy per chain F and writing
 , with
, with  and where we have assumed that the entropy of the branched structure is polynomial in the number of branches. This gives exponential suppression of branches when
and where we have assumed that the entropy of the branched structure is polynomial in the number of branches. This gives exponential suppression of branches when  according to
according to  . If the rings were to be synthesised from DNA, our analysis does not depend on whether or not the hairpins at the ends of the linear duplex structure are denatured or remain B-DNA. Furthermore, the DNA can still be driven into the gel by an external field that will generate a force (roughly) extensive in the DNA length that can therefore overcome even a very large constant hairpin energy penalty, being associated with the two ends (only).
. If the rings were to be synthesised from DNA, our analysis does not depend on whether or not the hairpins at the ends of the linear duplex structure are denatured or remain B-DNA. Furthermore, the DNA can still be driven into the gel by an external field that will generate a force (roughly) extensive in the DNA length that can therefore overcome even a very large constant hairpin energy penalty, being associated with the two ends (only). - 2
This would seem reasonable given that i) these fluctuations only give rise to changes in tube length that are a small fraction of the total tube length when
 , and ii) the dynamics associated with these fluctuations are fast compared with the slowest (reptative) modes.
, and ii) the dynamics associated with these fluctuations are fast compared with the slowest (reptative) modes. - 3
In each case we initially ran our MC code to perform ten consecutive complete stress relaxation processes which were used to calculate an estimated relaxation time
 . Our simulations then ran for a pre-equilibration period of
. Our simulations then ran for a pre-equilibration period of  , followed by
, followed by  during which the stress relaxation G(t) for all chains was recorded until the stress in all had completely relaxed, whereupon the stress relation process was (repeatedly) re-initiated. The mean stress relaxation time is then
during which the stress relaxation G(t) for all chains was recorded until the stress in all had completely relaxed, whereupon the stress relation process was (repeatedly) re-initiated. The mean stress relaxation time is then  .
.