Abstract
Chemical abundances are presented for 19 elements in a sample of 63 red giants in the Carina dwarf spheroidal galaxy (dSph), based on homogeneous 1D/LTE model atmosphere analyses of our own observations (32 stars) and data available in the literature (a further 31 independent stars). The (Fe) metallicity and [α/Fe] distribution functions have mean values and dispersions of −1.59 and 0.33 dex ([Fe/H] range: −2.68 to −0.64) and 0.07 and 0.13 dex ([α/Fe] range: −0.27 to 0.25), respectively. We confirm the finding of Venn et al. that a small percentage (some 10% in the present investigation) of the sample shows clear evidence for significant enrichment by Type Ia supernova (SN Ia) ejecta. Calcium, with the most accurately determined abundance of the α-elements, shows an asymmetric distribution toward smaller values of [Ca/Fe] at all [Fe/H], most significantly over −2.0 < [Fe/H] < −1.0, suggestive of incomplete mixing of the ejecta of SNe Ia with the ambient medium of each of Carina's generations. Approximate color–magnitude diagram age estimates are presented for the sample, and together with our chemical abundances, compared with the results of our previous synthetic color–magnitude diagram analysis, which reported the details of Carina's four well-defined populations. We searched for the Na–O anticorrelation universally reported in the Galaxy's globular clusters and confirm that this phenomenon does not exist in Carina. We also found that one of the 32 stars in our sample has an extremely enhanced lithium abundance—A(Li)NLTE = +3.36, consistent with membership of the ∼1% group of Li-rich stars in dSph described by Kirby et al.
1. Introduction
This is the second of two papers concerning the temporal and chemical evolution of the stellar populations of the Carina dwarf spheroidal (dSph) galaxy. In Paper I (Norris et al. 2017) we reported an analysis of Carina's color–magnitude diagram (CMD) to constrain the nature of the four populations evident in the very high quality CMD data of Stetson et al. (2011). As noted there, an understanding of the populations turns on a determination of their ages and chemical abundances, and while the age structure is best constrained by an interpretation of the CMD, a more complete understanding of the chemical evolution depends on an accurate knowledge of not only the abundance of iron ([Fe/H]) but also those of the some 20 elements that can be determined only from model stellar atmosphere analysis of high spectral resolution, high signal-to-noise ratio (S/N) spectroscopic data. That is, while the CMD is essential for the task of relatively accurate age determination, it does not strongly constrain the details of the system's chemical evolution, in particular the role of the α-elements. For that, a large sample of homogeneously analyzed high-resolution spectroscopic material is required to adequately constrain the details of Carina's chemical enrichment. To date the major high-resolution investigations are those of Shetrone et al. (2003), Koch et al. (2008), Venn et al. (2012), Lemasle et al. (2012), and Fabrizio et al. (2012, 2015). To further address this problem, we report here observations and analysis of 32 Carina red giants, together with reanalysis of the equivalent widths (EWs) from high-resolution spectra of a similar quality available in the literature for stars that include 31 Carina red giants not in our sample. These results together provide chemical abundances for a sample of 63 independent stars that have been analyzed homogeneously. We use these to seek clearer insight into the chemical enrichment of Carina's populations.
1.1. The Role of Carina in Constraining Dwarf Galaxy Enrichment
Carina is an interesting dSph galaxy, with a very complex star formation history as seen in its CMD (Smecker-Hane et al. 1994, 1996; Mighell 1997; Hurley-Keller et al. 1998; Hernandez et al. 2000; Dolphin 2002; Monelli et al. 2003; Bono et al. 2010; Stetson et al. 2011; de Boer et al. 2014; Monelli et al. 2014; Weisz et al. 2014; Kordopatis et al. 2016; Santana et al. 2016). Standard broadband BVRI photometry reveals several distinct sequences, clearly identifying a punctuated star formation history, with individual star-forming events of different epochs and durations. And yet, this dSph has one of the narrowest red giant branches in the Local Group. The degeneracy in age and metallicity/chemical composition on its red giant branch (RGB) seems to have conspired perfectly in these BVRI colors. It is clear that Carina is dominated by an intermediate-aged population, with minor contributions at both old and younger times. In Paper I we reported our investigation of the Carina CMD of Stetson et al. (2011) using synthetic CMDs based on the isochrones of Dotter et al. (2008), in terms of the three basic population parameters [Fe/H], age, and [α/Fe], for the cases when (i) [α/Fe] is held constant and (ii) [α/Fe] is permitted to vary. We found four epochs of star formation, well described in terms of [Fe/H] = −1.85, −1.5, −1.2, and ∼−1.15 and ages of ∼13, 7, ∼3.5, and ∼1.5 Gyr, respectively (for [α/Fe] = 0.1 (constant [α/Fe]) and [α/Fe] = 0.2, 0.1, 0.0, −0.2 (variable [α/Fe])), with small spreads in [Fe/H] and age of order 0.1 dex and 1–3 Gyr.4 (In Paper I we referred to these four groups chronologically, as the "first," "second," "third," and "fourth" populations, respectively. We shall adopt this nomenclature later in the present work.) These parameters reproduce five basic observed features in Carina's CMD (two distinct subgiant branches of old and intermediate-age populations, two younger, main-sequence components, and the small color dispersion observed on its RGB).
These complexities notwithstanding, dwarf galaxies such as Carina are simpler systems than spiral galaxies, having lower masses and having undergone fewer accretion episodes, fewer star formation events, and less chemical evolution (see, e.g., Mateo 1998; Tolstoy et al. 2009). Weisz et al. (2014) have shown significant scatter in the star formation history of the Local Group dSph galaxies, even among those with similar masses, indicating the importance of additional factors such as their local environment, the effects of stellar/supernova (SN) feedback, and variations in the metallicity yields and timescales for SN and asymptotic giant branch (AGB) events.
One aspect of current interest in dwarf galaxy research is the importance of inhomogeneous mixing of the interstellar medium (ISM). A poorly mixed ISM aids in the removal of low angular momentum gas in numerical simulations of dwarf galaxies, avoiding the formation of bulges (Governato et al. 2010). Inhomogeneous mixing has also been invoked to explain the large range in metallicities found in the ultrafaint galaxies, presumed to be due to a single core-collapse SN event (Simon et al. 2011; Tominaga et al. 2014, and Frebel & Norris 2015). We note that the metallicity dispersions observed in the ultrafaint systems are nevertheless in excellent agreement with the inhomogeneous and binomial model for the chemical evolution of galaxies presented by Leaman (2012).
The mixing efficiency and timescale for SN Ia events are less clear. The usual assumption is that SN Ia (and AGB) contributions lag those of SNe II by ∼1 Gyr (e.g., Argast et al. 2002; Revaz & Jablonka 2012), due to the lower mass of their progenitor stars. The location of a knee in the [α/Fe] versus [Fe/H] abundances for stars in dwarf galaxies compared with similar-metallicity stars in the Milky Way is one piece of evidence for the late contributions of iron from SN Ia—though that trend has also been attributed to metallicity-dependent SN Ia yields (Kobayashi et al. 1998 and Kobayashi & Nomoto 2009), or a truncated upper IMF (Tolstoy et al. 2003; McWilliam et al. 2013). It could be that several mechanisms are in play.
Direct evidence for inhomogeneous mixing of SN Ia material in a dwarf galaxy was presented for stars in Carina from ESO/FLAMES-UVES and Magellan/MIKE spectra by Venn et al. (2012). Two (of nine) stars showed an enhancement of the iron-group elements (Cr, Mn, Fe) by factors of 3–7 relative to the other elements, which suggested that those stars formed in a pocket of iron-enriched material; one of these (Car-612) is among the most metal-rich stars in Carina, suggesting late-time inhomogeneous mixing. Additional stars observed with ESO VLT FLAMES-GIRAFFE by Lemasle et al. (2012) also showed a wide dispersion in [X/Fe] values, but only three wavelength settings were used (covering ∼1000 Å), providing fewer elements to clearly identify the signatures of inhomogeneous mixing versus smooth/punctuated chemical evolution. Previous analyses of a few stars in Carina did not clearly identify these features as a result of too few stars (Shetrone et al. 2003) and elements (Koch et al. 2008) being analyzed.
1.2. Outline of the Present Work
We have undertaken a kinematic and chemical analysis of the 63 red giants in Carina in an effort to better understand the formation and evolution of this system. In Section 2 we present our observational material for 32 Carina red giants, based on high-resolution, moderate-S/N spectra obtained with the ESO/FLAMES-UVES combination during ESO Proposal 180.B-0806(B) (PI: G. Gilmore),5 which we use in Section 3 to determine chemical abundances for 19 elements for these stars, using model atmosphere techniques. In Section 4 we augment this data set with spectroscopic material of comparable quality for other Carina red giants in the literature. To produce a set of homogeneously determined abundances, we analyze the literature EW values using the same techniques as adopted for the primary sample. The total sample comprises 63 independent Carina red giants. Their [Fe/H] metallicity distribution function (MDF) is presented in Section 5, while Section 6 gives an overview of relative elemental abundances in the [X/Fe] versus [Fe/H] planes. In Section 7 we discuss the abundances of the α-elements and what they have to tell us about Carina's chemical evolution, while Section 8 examines the role played by SNe Ia in its chemical enrichment. In Sections 9 and Section 10 we present rough age estimates and compare them and our observed MDF and [α/Fe] distribution with those obtained using the synthetic CMD predictions in Paper I. Section 11 presents the result of our search for the ubiquitous anticorrelation between sodium and oxygen abundances that exists within individual Galactic globular clusters, while in Section 12 we present the discovery of an extremely lithium-rich Carina red giant. We summarize our results in Section 13.
2. Observational Material
The present high-resolution spectroscopic investigation of Carina is part of a larger program involving the kinematic and abundance analysis of a much larger sample of Carina giants observed at lower resolution. It utilizes the power of the ESO VLT FLAMES-UVES system in UVES-Fiber mode (Pasquini et al. 2002), which permits simultaneous observation of a large number of stars at intermediate resolution (R ∼ 6500), via a system of 130 fibers, together with a smaller number at high resolution (R ∼ 47,000), via eight fibers. The analysis of the lower-resolution sample has been reported elsewhere (Kordopatis et al. 2016). The obvious advantage of the higher-resolution capability is that it enables insight into the chemical abundances of considerably more elements (∼20) than is possible at the lower resolution. We refer the reader to our previous work on the Bootes I ultrafaint galaxy for an example of the synergy of the approach we adopt in the analysis of FLAMES material (see Koposov et al. 2011; Gilmore et al. 2013).
2.1. Sample Selection
Our selection of objects is based on unpublished CCD V, I observations that we have made of the Carina galaxy. The only criterion we adopted in the selection was that a star should lie close to the well-defined RGB of the system.6 In Figure 1 we show the positions of these stars in the () CMD, together with that of the larger sample surveyed, for the sample described by Stetson et al. (2011) and made available by P. B. Stetson (2014, private communication). The large red star symbols represent objects for which we have obtained the high-resolution spectra discussed above. The large green circles stand for stars having high-resolution spectroscopic data in the literature, to which we shall return in Section 4 and determine chemical abundances, using the techniques we adopt in the analysis of our program stars.
Figure 1. Carina () CMD for stars observed in our initial photometric survey. The high-quality photometry presented here has been made available by P. B. Stetson. The small black filled circles present results for the general survey, large red star symbols represent objects observed spectroscopically at high resolution in the present work, and large green filled circles stand for independent stars in the literature having spectroscopy of a similar quality.
Download figure:
Standard image High-resolution image2.2. High-resolution Spectroscopy
High-resolution, moderate-S/N spectra were obtained of 39 Carina red giants, during 2007 November–2008 March, with the FLAMES system at the 8.2 m Kueyen (VLT/UT2) telescope at Cerro Paranal, in UVES-Fiber mode. Of the eight UVES fibers, approximately five were allocated to Carina candidate members and approximately three to nearby sky positions to enable background measurement. We obtained nine individual exposures in Service Mode, eight of duration 60 minutes, leading to an effective total integration time of 8.8 hr. The spectra were obtained using the 580 nm setting and cover the wavelength ranges 4800–5750 Å and 5840–6800 Å. The resolving power was R = 47,000.
The spectra of the individual exposures of the program stars were reduced by using the FLAMES-UVES pipeline (Freudling et al. 2013).7 Following this, the individual spectra were cross-correlated to determine relative wavelength shifts between them in order to compensate for Earth's motion during the data-taking interval. After sky-subtracting and shifting the individual spectra to the rest frame, the spectra were co-added to produce the summed spectrum of each star. Our subsequent abundance analysis of these data indicated that the S/N of the spectra of seven objects was too low to permit reliable abundance results, and these will not be considered further here.
Details of the remaining 32 program stars are presented in Table 1, where columns (1) and (2) contain their identification and coordinates. Alternative nomenclatures of these stars, together with the names of others that will be the subject of reanalysis of equivalent data available in the literature, using techniques described below in Section 3, are presented in Table 14 of the Appendix.
Table 1. Coordinates, Photometry, and Radial Velocities for 32 Carina Red Giants
| Object | R.A. (2000) Decl. (2000) | V | B − V | I | J | H | K | Vrad | σ(Vrad) |
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| CC06122 | 06 41 39.64 −50 49 58.8 | 17.60 | 1.43 | 16.18 | 15.23 | 14.48 | 14.34 | 230.31 | 0.08 |
| CC06486 | 06 41 46.00 −50 51 00.6 | 18.17 | 1.24 | 16.89 | 16.01 | 15.41 | 15.27 | 226.23 | 0.19 |
| CC06975 | 06 42 10.86 −50 52 20.6 | 18.38 | 1.11 | 17.13 | 16.23 | 15.65 | 15.55 | 229.57 | 0.18 |
| CC07452 | 06 40 58.46 −50 53 35.5 | 17.80 | 1.29 | 16.41 | 15.52 | 14.88 | 14.74 | 225.23 | 0.09 |
| CC07889 | 06 41 40.83 −50 54 45.8 | 18.55 | 1.06 | 17.34 | 16.53 | 15.97 | 15.83 | 236.29 | 0.27 |
| CC08447 | 06 41 10.54 −50 55 53.0 | 17.99 | 1.25 | 16.65 | 15.72 | 15.09 | 14.94 | 232.52 | 0.10 |
| CC08469 | 06 42 17.43 −50 55 55.3 | 17.81 | 1.29 | 16.43 | 15.47 | 14.80 | 14.64 | 223.63 | 0.11 |
| CC08615 | 06 41 49.58 −50 56 11.5 | 18.50 | 1.05 | 17.32 | 16.45 | 15.93 | 15.78 | 223.91 | 0.21 |
| CC08695 | 06 41 36.49 −50 56 23.3 | 17.88 | 1.29 | 16.53 | 15.53 | 14.90 | 14.74 | 228.46 | 0.08 |
| CC08788 | 06 41 50.10 −50 56 35.2 | 18.59 | 1.04 | 17.41 | 16.56 | 16.03 | 15.92 | 228.31 | 0.11 |
| CC09000 | 06 41 54.60 −50 57 00.9 | 17.67 | 1.49 | 16.10 | 15.06 | 14.44 | 14.27 | 230.46 | 0.14 |
| CC09179 | 06 41 17.93 −50 57 20.5 | 18.30 | 1.13 | 17.04 | 16.14 | 15.58 | 15.46 | 233.00 | 0.19 |
| CC09225 | 06 41 19.70 −50 57 25.6 | 18.01 | 1.21 | 16.71 | 15.74 | 15.14 | 15.02 | 220.18 | 0.07 |
| CC09226 | 06 41 12.30 −50 57 26.1 | 18.33 | 1.04 | 17.13 | 16.25 | 15.69 | 15.57 | 219.84 | 0.20 |
| CC09430 | 06 42 05.38 −50 57 48.6 | 18.26 | 1.15 | 16.98 | 16.07 | 15.48 | 15.35 | 223.54 | 0.19 |
| CC09507 | 06 41 54.08 −50 57 56.8 | 18.31 | 1.06 | 17.13 | 16.29 | 15.73 | 15.58 | 227.39 | 0.20 |
| CC09633 | 06 41 53.85 −50 58 11.2 | 17.88 | 1.21 | 16.53 | 15.62 | 15.04 | 14.90 | 219.04 | 0.25 |
| CC09869 | 06 40 56.96 −50 58 38.4 | 18.11 | 1.20 | 16.81 | 15.89 | 15.28 | 15.13 | 219.07 | 0.07 |
| CC09929 | 06 41 54.84 −50 58 47.0 | 18.47 | 1.11 | 17.21 | 16.31 | 15.72 | 15.57 | 217.07 | 0.27 |
| CC10038 | 06 42 02.81 −50 58 59.5 | 18.25 | 1.16 | 16.98 | 16.06 | 15.45 | 15.32 | 222.85 | 0.11 |
| CC10194 | 06 40 30.85 −50 59 15.4 | 17.76 | 1.29 | 16.38 | 15.38 | 14.77 | 14.62 | 215.26 | 0.20 |
| CC10318 | 06 41 57.63 −50 59 32.8 | 17.97 | 1.25 | 16.61 | 15.65 | 14.99 | 14.84 | 222.46 | 0.15 |
| CC10414 | 06 41 47.63 −50 59 44.2 | 18.13 | 1.19 | 16.84 | 15.92 | 15.29 | 15.13 | 222.14 | 0.18 |
| CC10686 | 06 41 27.18 −51 00 18.4 | 17.75 | 1.30 | 16.36 | 15.37 | 14.69 | 14.55 | 232.56 | 0.08 |
| CC10690 | 06 41 16.31 −51 00 18.7 | 18.14 | 1.16 | 16.84 | 15.92 | 15.33 | 15.19 | 222.15 | 0.22 |
| CC10802 | 06 41 27.55 −51 00 34.9 | 18.64 | 1.06 | 17.45 | 16.61 | 15.99 | 15.83 | 236.63 | 0.24 |
| CC10944 | 06 41 16.76 −51 00 54.1 | 17.78 | 1.28 | 16.46 | 15.52 | 14.88 | 14.75 | 220.43 | 0.15 |
| CC11217 | 06 41 05.01 −51 01 36.0 | 17.62 | 1.37 | 16.20 | 15.20 | 14.50 | 14.37 | 220.78 | 0.12 |
| CC11388 | 06 40 58.04 −51 02 00.3 | 17.92 | 1.20 | 16.62 | 15.68 | 15.07 | 14.94 | 224.83 | 0.22 |
| CC11560 | 06 40 59.29 −51 02 26.7 | 18.14 | 1.15 | 16.87 | 15.98 | 15.38 | 15.23 | 217.57 | 0.12 |
| CC12038 | 06 41 00.31 −51 03 43.1 | 18.42 | 1.10 | 17.19 | 16.29 | 15.70 | 15.58 | 223.79 | 0.29 |
| CC12039 | 06 41 21.98 −51 03 43.3 | 17.78 | 1.27 | 16.42 | 15.50 | 14.83 | 14.71 | 219.02 | 0.07 |
A machine-readable version of the table is available.
Download table as: DataTypeset image
2.3. Photometry
Photometry has been obtained from several sources: P. B. Stetson provided us with homogenized BVI, M. J. Irwin furnished JHK from ESO VISTA survey photometry, and M. Gullieuszik supplied BVIJHKs. Here all BVI magnitudes are corrected to the Johnson–Kron–Cousins system, following Stetson (2005), while JHKs are corrected to be on the Two Micron All Sky Survey (2MASS) system. A comparison of the photometric data set per star between the three sources shows excellent agreement. We estimate from intercomparison of the photometry that the B, V, I, J, H, and K values have errors of 0.006, 0.006, 0.011, 0.009, 0.009, and 0.016, respectively. We have therefore averaged the magnitudes, and we present the results in Table 1, which we use in our determination of the atmospheric parameters in Section 3.1.
2.4. Radial Velocities
Radial velocities were measured for each of the individual spectra for each star described above. To do this, we used the Fourier cross-correlation techniques described by Norris et al. (2010, Section 2.4) and Gilmore et al. (2013, Section 2.2.1), to which we refer the reader for details. We note here, for completeness, that there were two minor differences in the present work. First, we cross-correlated our spectra against the Arcturus high-resolution spectrum of Hinkle et al. (2000)8 (rebinned to have the same pixel size as our data). Second, for each spectrum we cross-correlated over the three wavelength regions 5160–5190 Å, 5400–5498 Å, and 6502–6598 Å to produce three velocity estimates, which we averaged to determine the velocity for that spectrum. Then, for each star we averaged the velocities available for the approximately eight exposures of each star and (having applied appropriate heliocentric corrections) averaged these values, weighted by the inverse square of their errors, to produce the final radial velocity for each object. Our velocities and their internal errors are presented in the final two columns of Table 1. The data are of high precision, with the mean of the errors for the 32 stars being 0.16 km s−1. Velocities for these spectra have also been determined by Fabrizio et al. (2012): comparison between our velocities and theirs shows that the mean velocity difference is 0.03 km s−1 with a dispersion of 0.76 km s−1. The mean radial velocity of our sample of 32 stars (all of which are radial velocity members) is 224.8 ± 1.0 km s−1, with dispersion 5.65 ± 0.71 km s−1. We note that the dispersion agrees well with those of Walker et al. (2009b), within the limits, but is somewhat lower than those of 10.4 ± 1 km s−1, 7.6 ± 0.5 km s−1, and 8.5 ± 0.8 km s−1, reported by Kordopatis et al. (2016) for their metal-poor, intermediate-metallicity, and metal-richer RGB stars. For completeness, we also note that we find no dependence of velocity dispersion on metallicity in our relatively small sample of stars.
2.5. Equivalent Widths
Before attempting to determine EWs from the co-added pipelined spectra described in Section 2.2, we undertook three further steps. First, given the somewhat low S/N of a significant number of spectra and the line crowding on some of the relatively high abundance stars in our sample, we resolved to measure EWs only redward of 5300 Å. Inspection of the degree of line blending in the high-resolution spectrum of Arcturus (Hinkle et al. 2000) supports this decision. We also note the previous decision of Norris et al. (1995) in their abundance analysis of the red giants in the globular cluster ω Centauri (of spectra having R ∼ 38,000), who stated, "Initially we sought to measure ... all lines in the wavelength range 5050–6810 Å, but in view of the difficulty of continuum placement in the coolest stars, decided to reduce this to 5285–6810 Å." Second, given the high resolution (R = 47,000) of the present spectra, we double-binned the data to facilitate reliable continuum placement (yielding a pixel size of ∼0.028 Å).9 We measured S/N per double-binned pixel in several intervals of width 2.0–5.5 Å in the range 5310–5723 Å, in which the continuum is clearly seen in the Arcturus spectrum of Hinkle et al. (2000). The S/N values (averaged over the several wavelength intervals) for the 32 Carina giants for which we analyze EWs lie in the range of 8–22, with a median value of 12, and are presented for the individual stars in the first rows of Tables 2–4. Third, and finally, we removed the interorder undulations in the pipelined data and renormalized the spectra by determining the position of the "continuum" using five-pixel Gaussian smoothing and fitting a low-order Legendre polynomial, followed by k-sigma clipping using a scale length of 10 Å, following Venn et al. (2012). Examples of the resulting spectra in the wavelength range 5160–5200 Å, including for interest that of the α-challenged star Car-612 discussed in Section 1 (and designated here CC07452), are presented in Figure 2. (We note that these spectra lie outside the region of our abundance analysis; they are presented here for heuristic purposes only.)
Figure 2. Representative spectra of the program stars in the wavelength range 5160−5200 Å. Also shown are atmospheric parameters and abundances //[Fe/H]/[Ca/Fe], where the values are those determined in the present work, as will be described below. [Fe/H] increases from top to bottom, and the accompanying increase in line strength is clear. We note that all of the stars, except CC07452 (=Car-612), have [Ca/Fe] ∼ 0.05−0.10. CC07452, with [Ca/Fe] = −0.32, is "α-challenged," an effect first established by Koch et al. (2008) and Venn et al. (2012) and described in the Introduction. Inspection of the red-colored parts of the spectra, which cover unblended features of the α-elements Mg i, Ti i, and Ti ii, shows the important result (which we shall revisit in Section 8) that not only Ca but also Mg and Ti have lower abundances relative to Fe in CC07452 than in the majority of the stars.
Download figure:
Standard image High-resolution imageTable 2. Atomic Data and Equivalent Widths (mÅ) for 11 Carina Red Giants
| Species | Wavelength | χ | log gf | CC06122 | CC06486 | CC06975 | CC07452 | CC07889 | CC08447 | CC08469 | CC08615 | CC08695 | CC08788 | CC09000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) |
| S/Na | ⋯ | ⋯ | ⋯ | 17 | 10 | 8 | 18 | 9 | 16 | 11 | 11 | 14 | 10 | 23 |
| W(min)(mÅ) | ⋯ | ⋯ | ⋯ | 26 | 28 | 31 | 14 | 34 | 24 | 24 | 20 | 23 | 23 | 20 |
| Fe i | 5302.30 | 3.28 | −0.880 | 153.5 | ⋯ | 126.3 | 144.5 | 66.5 | 122.7 | 147.7 | 115.0 | 143.3 | 121.7 | 140.7 |
| Fe i | 5307.37 | 1.61 | −2.912 | 183.0 | 90.5 | 113.7 | 162.0 | 57.0 | 136.3 | 166.7 | 117.3 | 138.3 | 109.0 | 145.0 |
| Fe i | 5324.19 | 3.21 | −0.100 | 186.5 | ⋯ | ⋯ | ⋯ | 118.5 | 186.5 | 182.0 | ⋯ | 181.0 | ⋯ | 193.0 |
| Fe i | 5332.90 | 1.56 | −2.780 | ⋯ | ⋯ | 103.0 | 192.5 | 68.5 | ⋯ | ⋯ | ⋯ | 168.5 | ⋯ | ⋯ |
| Fe i | 5339.93 | 3.27 | −0.720 | 139.5 | 102.0 | ⋯ | 160.5 | 29.5 | 144.3 | 147.3 | 110.0 | 157.3 | 143.5 | 147.3 |
Note.
aS/N per ∼0.28 Å pixel at 5300−5700 Å.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 3. Atomic Data and Equivalent Widths (mÅ) for 11 Carina Red Giants
| Species | Wavelength | χ | log gf | CC09179 | CC09225 | CC09226 | CC09430 | CC09507 | CC09633 | CC09869 | CC09929 | CC10038 | CC10194 | CC10318 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) |
| S/Na | ⋯ | ⋯ | ⋯ | 13 | 18 | 14 | 12 | 13 | 11 | 12 | 8 | 12 | 9 | 10 |
| W(min)(mÅ) | ⋯ | ⋯ | ⋯ | 20 | 20 | 20 | 25 | 22 | 29 | 25 | 30 | 22 | 26 | 25 |
| Fe i | 5302.30 | 3.28 | −0.880 | 83.7 | 129.0 | 98.0 | 73.0 | 97.0 | 54.0 | 127.7 | 118.0 | 133.0 | 124.0 | 129.0 |
| Fe i | 5307.37 | 1.61 | −2.912 | 90.3 | 132.3 | 116.5 | 89.5 | 101.0 | 62.0 | 162.0 | 72.0 | 131.7 | 179.5 | ⋯ |
| Fe i | 5324.19 | 3.21 | −0.100 | ⋯ | ⋯ | 147.5 | ⋯ | ⋯ | 94.5 | 186.0 | ⋯ | ⋯ | ⋯ | ⋯ |
| Fe i | 5332.90 | 1.56 | −2.780 | ⋯ | ⋯ | ⋯ | ⋯ | 119.0 | ⋯ | 158.0 | ⋯ | ⋯ | ⋯ | 145.5 |
| Fe i | 5339.93 | 3.27 | −0.720 | 130.0 | 148.7 | 130.7 | 102.0 | 116.0 | 46.0 | 136.0 | ⋯ | 121.7 | 140.5 | 153.7 |
Note.
aS/N per ∼0.28 Å pixel at 5300−5700 Å.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 4. Atomic Data and Equivalent Widths (mÅ) for 10 Carina Red Giants
| Species | Wavelength | χ | log gf | CC10414 | CC10686 | CC10690 | CC10802 | CC10944 | CC11217 | CC11388 | CC11560 | CC12038 | CC12039 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) |
| S/Na | ⋯ | ⋯ | ⋯ | 9 | 20 | 14 | 7 | 16 | 16 | 10 | 11 | 8 | 18 |
| W(min)(mÅ) | ⋯ | ⋯ | ⋯ | 26 | 15 | 25 | 33 | 20 | 22 | 26 | 23 | 24 | 22 |
| Fe i | 5302.30 | 3.28 | −0.880 | 118.5 | 126.3 | 97.0 | ⋯ | 101.0 | 155.0 | ⋯ | 106.5 | 132.5 | 141.3 |
| Fe i | 5307.37 | 1.61 | −2.912 | 166.7 | 134.0 | 115.5 | 120.5 | 121.0 | 166.3 | 145.5 | 109.0 | 98.3 | 139.7 |
| Fe i | 5324.19 | 3.21 | −0.100 | ⋯ | ⋯ | 130.0 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 178.0 |
| Fe i | 5332.90 | 1.56 | −2.780 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 155.0 | ⋯ | ⋯ |
| Fe i | 5339.93 | 3.27 | −0.720 | 162.5 | 126.3 | 109.0 | 133.7 | 106.7 | 164.3 | ⋯ | 109.5 | 132.5 | 143.3 |
Note.
aS/N per ∼0.28 Å pixel at 5300−5700 Å.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
EWs were measured independently for all stars by both J.E.N. and D.Y. for the set of unblended lines formed by the merging of the line lists of Venn et al. (2012) and Yong et al. (2013). Three independent equivalent measures were obtained: J.E.N. used the EW measurement techniques described by Norris et al. (2001), while D.Y. utilized IRAF software as described by Yong et al. (2008), as well as the automated package DAOSPEC (see Stetson & Pancino 2008).10 As a further check, K.A.V. used IRAF and DAOSPEC for a small subset of the spectra, which confirms the results of J.E.N. and D.Y.
Before accepting an EW measurement, both J.E.N. and D.Y. inspected the Gaussian fits to each spectrum line to ensure an acceptable representation. For each line in a given star, the measurements of J.E.N. and D.Y. produced three independent estimates that were combined as follows: (i) we required that at least two estimates were available; (ii) when three measurements were recorded, we rejected one of them if it clearly disagreed with the average of the other two; and (iii) of the cases where two estimates were averaged, we rejected some 30 lines for which large differences of order greater than 3σ existed between them. We rejected a line from the abundance analysis if an EW was measured for it in only one star, or the majority of stars in the sample had an EW greater than 200 mÅ. Finally, in four cases we rejected a line that was the only representative of an atomic species and yielded an abundance that was clearly in error. Figure 3 presents a comparison of the EWs of the present work with those of Shetrone et al. (2003), Koch et al. (2008), Venn et al. (2012), Lemasle et al. (2012), and Fabrizio et al. (2012, 2015). In these comparisons, there is good agreement between the present work and the results of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012).
Figure 3. Comparison of the EWs of the present work with those of (a) Shetrone et al. (2003), (b) Koch et al. (2008), (c) Venn et al. (2012), (d) Lemasle et al. (2012), and (e) Fabrizio et al. (2012). In the upper left corner of each panel the top line presents the star identification we use, while the next line contains the name used by the other authors. The black line is the 1:1 relationship, while the red line represents the linear least-squares linear best fit. The mean difference in EWs, (in the sense other work – this work), its standard error, and dispersion (σ) are also shown.
Download figure:
Standard image High-resolution imageWe find a systematic difference, however, between our data and those of Koch et al. (2008) between their LG04a_01826 and our CC07452, in the sense that their EWs become systematically smaller than ours with increasing line strength. (Note, however, that Figure 3 shows good agreement between our work and that of Venn et al. [2012] for this object.) We have five other stars (CC06122, CC08469, CC10194, CC11217, CC12039) in common with the work of Koch et al. (2008) and find similar differences in all of these objects as well. In Section 4, when we reanalyze EW data from the literature, we will not include the work of Koch et al. (2008) in view of these systematic EW differences.
We obtain relatively poor agreement between our results and those of Fabrizio et al. (2012, 2015) for CC10686, as may be seen in the bottom panel of Figure 3. To investigate this further, in the top left panel of Figure 4 we present a comparison between the EWs of Fe i lines in the 31 stars in common between the samples of Fabrizio et al. (2012) and the present work,11 and in the bottom left panel we compare the collective Fe i data of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012) on the one hand and the present work on the other. In the top right panel of the figure we present a similar comparison for the non-Fe lines, using the EWs of Fabrizio et al. (2015). From these panels we conclude that the line strengths of Fabrizio et al. (2012, 2015) are on average smaller than those of both the present investigation and those of the other workers. As seen in Figure 4, the EWs of Fabrizio et al. (2012) and Fabrizio et al. (2015) are smaller by 18 and 15 mÅ for Fe i and non-Fe lines, respectively, than those of the present work. Offsets of this order in comparison with the work of Venn et al. (2012) and Lemasle et al. (2012) were also reported by Fabrizio et al. (2015). We shall return to the significance of these differences in Section 3.4.
Figure 4. Comparison of the Fe i EWs, W, of stars in common between the present work and those of Fabrizio et al. (2012) (top left panel) and those of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012) (bottom left panel), and between the EWs of non-Fe lines of the present work and those of Fabrizio et al. (2015) (top right panel) and those of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012) (bottom right panel). The mean difference in EWs, (in the sense other work – this work), its standard error, and dispersion (σ) are also shown.
Download figure:
Standard image High-resolution imageAs part of our quality control, we estimated the smallest EW, W(min), that we could reliably measure in each star. To achieve this, for each spectrum we examined the number of lines we measured as a function of decreasing EW, and on the conservative assumption that at lowest line strength our estimates might not be reliable, we adopted the fifth-smallest EW we measured as a conservative estimate of W(min). These values lie in the range of 14–34 mÅ, with median 24 mÅ, and are presented in the second row of Tables 2–4. If we use the Cayrel (1988) formula, with the correction from Battaglia et al. (2008), to calculate the minimum EW, we find a range from 4 mÅ (S/N = 22) to 11 mÅ (S/N = 8) for our high-resolution data. These values are a factor of three smaller than our conservative estimates above and therefore are consistent with a 3σ certainty for these estimates.
In Section 11 we shall investigate the existence or otherwise of anticorrelation between the abundances of Na and O, which is ubiquitous within individual Galactic globular clusters, and which the work of Shetrone et al. (2003) suggests may not exist in Carina. As part of that exercise we closely estimated the upper limits of the EWs of the lines of these elements (together with Al, which also anticorrelates with O in the globular clusters) by visual inspection of them and nearby lines of other elements. These limits are also presented, for future consideration, in Tables 2–4, specifically for O i λ6300.3, Na i λ5688.2, and Al i λ6696.0.
To form our final EW data set, we accepted lines with wavelengths in the range of 5300–6780 Å and EWs less than 200 mÅ. Our adopted EWs for 211 unblended lines are presented in Tables 2–4. Line identifications, together with their lower excitation potentials, χ, and log gf values, are presented in columns (1)–(4), respectively. The EWs populate the remainder of the tables. These data are suitable for model atmosphere abundance analysis (see Section 3).
In what follows we shall exclude lines weaker than the relevant W(min) values described above, except for the O i λ6300.3, Na i λ5688.2, and Al i λ6696.0 transitions, discussed in the previous paragraph. We consider these weaker lines, but we note that their detections are at the 1σ–2σ level, rather than the 3σ level we have adopted for the other lines.
3. Chemical Abundance Analysis
3.1. Atmospheric Parameters
3.1.1. Effective Temperature ()
In most abundance analyses of cool giants, effective temperatures are based on either spectroscopic or photometric techniques. The former, denoted "excitation" temperatures, are based on the requirement that model atmosphere analysis of Fe i lines should yield abundances independent of lower excitation potential, while the latter, denoted "photometric" temperatures, rely on calibrations of the stellar continuum energy distribution as a function of effective temperature. Insofar as our spectra have relatively low S/N, on the one hand, while we have access to accurate BVIJHK photometry, on the other, we have chosen to adopt photometric temperatures, which we expect to have considerably higher accuracy in the present case.
We have determined by using the infrared flux method (IRFM), following Casagrande et al. (2006), which solves for in the basic equation
where and refer to bolometric and monochromatic infrared fluxes at the Earth, while refers to a corresponding model atmosphere synthetic spectrum.
The observational input data were the BVIJHK values presented in Table 1 and a distance modulus and reddening for Carina of = 20.05 ± 0.11 and E(B − V) = 0.06 ± 0.02 (Venn et al. 2012, Section 3.4), while the adopted model synthetic spectra were those of Castelli & Kurucz (2003). As found by Casagrande et al. (2006), these temperatures tend to be slightly ( K) hotter than those determined with the Ramírez and Meléndez (2005) BVIJHK color–temperature calibrations. They tracked this effect primarily to the zero-point calibration of the 2MASS photometric system. The resulting , which are the averages of the three independent estimates obtained by applying the IRFM to the observed J, H, and K magnitudes, are presented in column (2) of Table 5, while column (3) contains their uncertainties, based on the spread in the JHK estimates. The average uncertainty in the for the 32 stars in the table is 76 ± 2 K, which we shall use in Section 3.3.
Table 5. Model Atmosphere Parameters for 32 Carina Red Giants
| Object | σ | [M/H] | ξt | ||
|---|---|---|---|---|---|
| (K) | (K) | (cgs) | (dex) | (km s−1) | |
| (1) | (2) | (3) | (4) | (5) | (6) |
| CC06122 | 4284 | 60 | 0.68 | −1.5 | 2.30 |
| CC06486 | 4524 | 62 | 1.07 | −2.0 | 1.95 |
| CC06975 | 4563 | 84 | 1.18 | −1.8 | 2.30 |
| CC07452 | 4437 | 65 | 0.87 | −1.3 | 2.30 |
| CC07889 | 4675 | 55 | 1.31 | −2.3 | 2.30 |
| CC08447 | 4418 | 72 | 0.93 | −1.5 | 2.15 |
| CC08469 | 4337 | 68 | 0.81 | −1.5 | 2.25 |
| CC08615 | 4651 | 84 | 1.28 | −1.7 | 2.40 |
| CC08695 | 4337 | 89 | 0.84 | −1.3 | 2.10 |
| CC08788 | 4695 | 82 | 1.34 | −1.5 | 2.45 |
| CC09000 | 4230 | 116 | 0.67 | −1.8 | 2.40 |
| CC09179 | 4561 | 87 | 1.15 | −1.8 | 1.85 |
| CC09225 | 4438 | 93 | 0.95 | −1.6 | 2.15 |
| CC09226 | 4619 | 76 | 1.19 | −1.5 | 1.90 |
| CC09430 | 4509 | 74 | 1.10 | −2.1 | 1.95 |
| CC09507 | 4652 | 63 | 1.20 | −1.7 | 2.15 |
| CC09633 | 4487 | 80 | 0.93 | −2.2 | 2.40 |
| CC09869 | 4459 | 74 | 1.01 | −1.3 | 2.10 |
| CC09929 | 4515 | 73 | 1.19 | −1.5 | 2.10 |
| CC10038 | 4486 | 73 | 1.08 | −1.2 | 1.95 |
| CC10194 | 4352 | 98 | 0.80 | −1.7 | 2.05 |
| CC10318 | 4359 | 69 | 0.89 | −1.5 | 2.10 |
| CC10414 | 4442 | 66 | 1.01 | −1.4 | 2.30 |
| CC10686 | 4312 | 73 | 0.76 | −1.6 | 2.05 |
| CC10690 | 4486 | 78 | 1.04 | −1.9 | 2.25 |
| CC10802 | 4587 | 72 | 1.30 | −1.3 | 2.00 |
| CC10944 | 4425 | 69 | 0.85 | −1.9 | 2.40 |
| CC11217 | 4279 | 78 | 0.69 | −1.4 | 2.30 |
| CC11388 | 4454 | 81 | 0.93 | −1.5 | 2.45 |
| CC11560 | 4514 | 68 | 1.06 | −1.5 | 2.20 |
| CC12038 | 4551 | 73 | 1.19 | −1.6 | 1.95 |
| CC12039 | 4412 | 65 | 0.84 | −1.6 | 2.35 |
A machine-readable version of the table is available.
Download table as: DataTypeset image
3.1.2. Surface Gravity ()
In many analyses surface gravities are determined by requiring that abundances obtained by using Fe i and Fe ii lines are the same. There are two potential problems with this method. The first is that the results of non-LTE (NLTE) calculations show that while the LTE assumption is acceptable for the analysis of Fe ii lines, it leads to erroneous results for Fe i (e.g., Lind et al. 2012). An additional consideration is that at lowest abundances the number of Fe ii lines decreases dramatically. A second method of gravity determination is to use theoretical isochrones in which the observed is interpolated in the theoretical (, ) relationship, or (with color as proxy for ) in a (, color) relationship. This method is, however, critically dependent on the accuracy of the model values and the (color, ) dependence.
A third approach is to use the fundamental definitions of gravity and to express gravity as a function of mass, , and luminosity. The basic challenge of this method is that one needs a reliable distance in order to determine luminosity, which is not generally possible for field stars. For star clusters, however, this is not an insuperable problem, insofar as their distances can be obtained with reasonable accuracy. We choose to follow this approach.
The surface gravity, , of a star of mass M, effective temperature , and bolometric magnitude MBol, may be written as
To apply this relationship, we adopt for the Sun ⊙ = 4.44, Teff⊙ = 5777 K, and MBol⊙ = 4.75, and for the Carina giants we adopt M = 0.8 M⊙, the distance modulus and reddening of Section 3.1.1, and A(V)/E(B − V) = 3.24 (following Schlegel et al. 1998; Venn et al. 2012). We use the V magnitudes in Table 1, together with V bandpass bolometric corrections (BCs) from Alonso et al. (1999), to determine . The resulting gravities are presented in column (4) of Table 5.
The error budget for may be expressed as
We estimate the following representative errors: σM/M =0.26 assuming that the bulk of the stars in our sample have ages in the range of 5–12 Gyr and [α/Fe] in the range of −0.2 to 0.4 dex, together with the isochrones of Dotter et al. (2008),12 and noting that this estimate is relatively insensitive to metal abundance; / = 0.019 (Section 3.1.1); σV = 0.020 (Section 2.3); = 0.110 (Section 3.1.1); and σ(BC) = 0.048 (following Alonso et al. 1999), with = 80 K and = 0.15 (Section 3.3). With these values σlogg = 0.07 dex, and we note in passing that errors in are the dominant contributor to the total error budget.
3.1.3. Metal Abundance ([M/H])
We assume that from the point of view of model atmosphere analysis, the metallicity [M/H] and iron abundance [Fe/H] are synonymous. Throughout our abundance analysis we have iterated the metal abundance of the models at each determination of the abundances to be the same as those obtained on the previous run: column (5) of Table 5 contains our final adopted model values of [Fe/H]. The average uncertainty for the stars in the table is 0.14 dex. (See Section 3.3, Table 6.)
3.2. Abundance Determination
Chemical abundances were determined by using the model atmosphere techniques described in Norris et al. (2010, Section 3), Yong et al. (2013, Section 2), and Gilmore et al. (2013, Section 3.1), to which we refer the reader. Here, we provide only some of the details of our procedures. As before, we adopted the ATLAS9 models of Castelli & Kurucz (2003)13 (plane-parallel, 1D, LTE), with α-enhancement [α/Fe] = +0.4 and microturbulent velocity ξt = 2 km s−1. The analysis of the EWs presented in Section 2.5 used the LTE stellar-line-analysis program MOOG (Sneden 1973), as modified by Sobeck et al. (2011), to include an improved treatment of continuum scattering. We took into account hyperfine splitting (HFS) for lines of Sc, V, Mn, Co, Cu, and Ba, using data from Kurucz & Bell (1995), and for La, we adopted HFS data from Ivans et al. (2006). For Ba, we assumed the McWilliam (1998) r-process isotopic composition, while for Cu, we assumed solar isotope ratios. Once the atmospheric parameters , , and chemical abundance [M/H] are given, one needs to determine the microturbulent velocity, ξt. We achieved this by requiring that the abundance determined from the Fe i lines should be independent of their EWs. During this procedure, we excluded Fe i lines that fell more than either 3σ or 0.5 dex from the mean value. Values of ξt are presented in column (6) of Table 5. Other authors have noted that ξt is a function of : we find ξt = 2.392–0.313 × , with an rms scatter of 0.003 km s−1, in excellent agreement with the relationship of Worley et al. (2013), who reported ξt = 2.386–0.313 × . In our error analysis below, we shall adopt an error = 0.2 km s−1.
Detailed results of the abundance analysis are presented in Table 6. In the 32 blocks of this table (one per star) columns (1)–(4) contain the atomic species, the mean absolute abundance log  (X) (=log(NX/NH) + 12.0), its standard error of the mean, s.e., and the number of lines analyzed, respectively. Column (5) presents [Fe/H] or [X/Fe], obtained by using the data in column (2) and the solar abundances of Asplund et al. (2009). In the calculation of [X/Fe], we adopted the value of [Fe/H] determined using the neutral species. Given the much larger number of Fe i lines, this leads to considerably higher precision in our relative abundances. Had we adopted [Fe ii/H], the precision of our [X/Fe] values would be considerably poorer given the small number (2–12) of available Fe ii lines. The question that then remains is, how accurate are the [X/Fe] results? In particular, what is the role of NLTE, which affects Fe i more than Fe ii? According to Lind et al. (2012, see their Figure 2), in our parameter range, the NLTE corrections are ≤+0.1 dex for Fe i and 0.0 for Fe ii. We shall discuss the role of these small effects in Section 6.
(X) (=log(NX/NH) + 12.0), its standard error of the mean, s.e., and the number of lines analyzed, respectively. Column (5) presents [Fe/H] or [X/Fe], obtained by using the data in column (2) and the solar abundances of Asplund et al. (2009). In the calculation of [X/Fe], we adopted the value of [Fe/H] determined using the neutral species. Given the much larger number of Fe i lines, this leads to considerably higher precision in our relative abundances. Had we adopted [Fe ii/H], the precision of our [X/Fe] values would be considerably poorer given the small number (2–12) of available Fe ii lines. The question that then remains is, how accurate are the [X/Fe] results? In particular, what is the role of NLTE, which affects Fe i more than Fe ii? According to Lind et al. (2012, see their Figure 2), in our parameter range, the NLTE corrections are ≤+0.1 dex for Fe i and 0.0 for Fe ii. We shall discuss the role of these small effects in Section 6.
Table 6. Chemical Abundances for 32 Carina Red Giants
| Species | log | s.e. | N | [X/Fe] | σSys[X/Fe] | σTot[X/Fe] |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| CC06122 | ||||||
| Fe i | 6.07 | 0.02 | 74 | −1.43a | 0.14 | 0.14 |
| O i | 7.58 | 0.17 | 1 | 0.32 | 0.13 | 0.21 |
| Na i | 4.61 | 0.17 | 1 | −0.20 | 0.08 | 0.19 |
| Mg i | 6.48 | 0.18 | 2 | 0.31 | 0.03 | 0.18 |
| Al i | <5.38 | 0.17 | 1 | <0.36 | 0.10 | 0.20 |
| Si i | 6.29 | 0.17 | 1 | 0.21 | 0.14 | 0.22 |
| Ca i | 5.09 | 0.04 | 19 | 0.09 | 0.02 | 0.04 |
| Sc ii | 1.89 | 0.14 | 5 | 0.17 | 0.11 | 0.18 |
| Ti i | 3.67 | 0.04 | 8 | 0.15 | 0.09 | 0.10 |
| Ti ii | 3.86 | 0.08 | 2 | 0.34 | 0.10 | 0.13 |
| V i | 2.43 | 0.11 | 10 | −0.07 | 0.11 | 0.16 |
| Cr i | 4.20 | 0.06 | 4 | −0.01 | 0.08 | 0.10 |
| Mn i | 3.68 | 0.04 | 5 | −0.32 | 0.06 | 0.07 |
| Fe ii | 6.16 | 0.04 | 8 | 0.09 | 0.17 | 0.17 |
| Co i | 3.53 | 0.17 | 1 | −0.03 | 0.08 | 0.19 |
| Ni i | 4.71 | 0.07 | 10 | −0.08 | 0.05 | 0.09 |
| Cu i | 2.13 | 0.17 | 1 | −0.63 | 0.08 | 0.19 |
| Ba ii | 1.19 | 0.08 | 3 | 0.44 | 0.11 | 0.14 |
| La ii | 0.16 | 0.08 | 3 | 0.49 | 0.10 | 0.13 |
| Nd ii | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| Eu ii | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
Note.
a[Fe/H].Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
3.3. Abundance Uncertainties
The random internal error (s.e.) of the abundances in column (3) of Table 6 is the standard error of the mean of the abundances from lines analyzed for each element. The abundances are also subject to systematic errors resulting from the uncertainties in our derived model parameters—, , [M/H], and ξt. The uncertainties we adopt for these quantities are σTeff = 80 K (Section 3.1.1), = 0.07 dex (Section 3.1.2), = 0.15 dex (see below in this section), and = 0.2 km s−1 (Section 3.2). For each of our program stars we varied , , [M/H], and ξt, one at a time, by these uncertainties to determine the corresponding abundance differences. Since we shall be interested mainly in relative abundances, [X/Fe], we have determined the corresponding uncertainties in those quantities, while for iron we estimated the uncertainty in [Fe i/H]. To determine the total systematic error, we co-added the four error contributions as follows: first, given that the error in is determined primarily by uncertainty in , we added the errors in and linearly; second, we then quadratically added this error to those associated with [M/H] and ξt. For heuristic purposes, Table 7 presents the average systematic abundance errors for the 32 program stars, where columns (1)–(6) contain the species, errors in , , [M/H], and ξt, and the total systematic error, respectively.
Table 7. Average Abundance Uncertainties in [Fe/H] and [X/Fe]
| Species | σTeff | ||||
|---|---|---|---|---|---|
| (80 K) | (0.07 dex) | (0.15 dex) | (0.2 km s−1) | ||
| (1) | (2) | (3) | (4) | (5) | (6) |
| Fe i a | 0.109 | −0.001 | −0.015 | −0.082 | 0.136 |
| O i | −0.099 | 0.029 | 0.097 | 0.078 | 0.128 |
| Na i | −0.043 | −0.004 | 0.000 | 0.070 | 0.084 |
| Mg i | −0.035 | −0.008 | 0.002 | 0.018 | 0.047 |
| Al i | −0.048 | −0.002 | 0.004 | 0.077 | 0.092 |
| Si i | −0.099 | 0.007 | 0.030 | 0.078 | 0.123 |
| Ca i | −0.015 | −0.005 | −0.010 | 0.016 | 0.027 |
| Sc ii | −0.115 | 0.028 | 0.074 | 0.042 | 0.111 |
| Ti i | 0.034 | −0.004 | −0.011 | 0.073 | 0.079 |
| Ti ii | −0.116 | 0.026 | 0.069 | 0.007 | 0.104 |
| V i | 0.051 | −0.004 | −0.011 | 0.071 | 0.086 |
| Cr i | 0.050 | −0.002 | −0.021 | −0.019 | 0.054 |
| Mn i | 0.025 | −0.002 | −0.006 | 0.052 | 0.057 |
| Fe ii | −0.163 | 0.032 | 0.079 | 0.053 | 0.153 |
| Co i | 0.000 | 0.002 | 0.015 | 0.083 | 0.084 |
| Ni i | −0.001 | 0.005 | 0.016 | 0.044 | 0.046 |
| Cu i | 0.004 | 0.004 | 0.016 | 0.086 | 0.087 |
| Ba ii | −0.080 | 0.027 | 0.074 | −0.064 | 0.100 |
| La ii | −0.084 | 0.028 | 0.079 | 0.075 | 0.111 |
| Nd ii | −0.082 | 0.028 | 0.073 | 0.051 | 0.092 |
| Eu ii | −0.110 | 0.025 | 0.077 | 0.073 | 0.126 |
Note.
aErrors pertain to uncertainties in [Fe/H].Download table as: ASCIITypeset image
To determine total error estimates, we adopted the following procedure (see Norris et al. 2010). The random errors in column (3) of Table 6 are based on the dispersion in what is often a small number of lines, and hence are themselves uncertain. We replace this estimated random error, s.e., from N lines, by max(, ). The second term is what one might expect from a set of N lines having the dispersion we obtained from our more numerous () Fe i lines. We then quadratically combine this updated random error and that associated with uncertainty in the atmospheric parameters from column (6) of Table 6 to obtain the total error, σ[X/Fe], which we present in column (7) of Table 6. The mean of the total error σ[Fe/H] for the 32 stars in Table 6 is 0.14 dex, which agrees well with the uncertainty dex we have adopted previously in this section.
3.4. Summary of Abundances and Comparison of Our Atmospheric Parameters with Those of Others
We summarize our essential abundance results—[Fe/H] and relative abundances [X/Fe]—for the 32 red giants, in Table 8, where the column structure of the table will be self-evident. For each star there are three rows: the first presents abundances, the second the corresponding total abundance errors, and the third the number of lines involved.
Table 8. Summarya of [Fe/H], [X/Fe], and Total Errors σTot for 32 Carina Red Giants
| Object | [Fe/H] | O | Na | Mg | Al | Si | Ca | Sc | Ti i | Ti ii | V | Cr | Mn | Fe ii | Co | Ni | Cu | Ba | La | Nd | Eu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CC06122 | −1.43 | 0.32 | −0.20 | 0.31 | < 0.36 | 0.21 | 0.09 | 0.17 | 0.15 | 0.34 | −0.07 | −0.01 | −0.32 | 0.09 | −0.03 | −0.08 | −0.63 | 0.44 | 0.49 | ⋯ | ⋯ |
| 0.14 | 0.21 | 0.19 | 0.18 | 0.20 | 0.22 | 0.04 | 0.18 | 0.10 | 0.13 | 0.16 | 0.10 | 0.07 | 0.17 | 0.19 | 0.09 | 0.19 | 0.14 | 0.13 | ⋯ | ⋯ | |
| 74 | 1 | 1 | 2 | 1 | 1 | 19 | 5 | 8 | 2 | 10 | 4 | 5 | 8 | 1 | 10 | 1 | 3 | 3 | ⋯ | ⋯ | |
| CC06486 | −2.03 | < 0.80 | 0.19 | 0.17 | < 1.28 | ⋯ | 0.11 | 0.14 | ⋯ | ⋯ | ⋯ | −0.16 | ⋯ | 0.42 | ⋯ | 0.08 | ⋯ | −0.45 | ⋯ | ⋯ | ⋯ |
| 0.16 | 0.29 | 0.28 | 0.12 | 0.28 | ⋯ | 0.09 | 0.29 | ⋯ | ⋯ | ⋯ | 0.13 | ⋯ | 0.30 | ⋯ | 0.11 | ⋯ | 0.23 | ⋯ | ⋯ | ⋯ | |
| 42 | 1 | 1 | 2 | 1 | ⋯ | 13 | 1 | ⋯ | ⋯ | ⋯ | 3 | ⋯ | 1 | ⋯ | 5 | ⋯ | 3 | ⋯ | ⋯ | ⋯ |
Note.
aFor each object the three rows contain [Fe/H] and [X/Fe], σTot, and the number of lines, respectively.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
In Figure 5 we compare our [Fe/H] values with those presented by Shetrone et al. (2003), Koch et al. (2006), Venn et al. (2012), Lemasle et al. (2012), and Fabrizio et al. (2012). The agreement in the figure is quite satisfactory, except that our values differ systematically from those of Fabrizio et al. (2012), for which there is considerable dispersion. At least part of the difference will result from the fact (see Section 2.5, Figure 4) that the EWs of Fabrizio et al. (2012) are on average smaller than those of the present work.
Figure 5. Comparison of the abundances, [Fe/H], of the present work with those of (a) Shetrone et al. (2003), (b) Koch et al. (2006) (using the Carretta & Gratton [1997] calibration), (c) Venn et al. (2012), (d) Lemasle et al. (2012), and (e) Fabrizio et al. (2012). The black line is the 1:1 relationship.
Download figure:
Standard image High-resolution imageWe are now in a position to compare our atmospheric parameters with those of Shetrone et al. (2003), Koch et al. (2008), Venn et al. (2012), Lemasle et al. (2012), and Fabrizio et al. (2012). In what follows we present the mean differences in , , and [Fe/H] (in the sense present work — other work), together with N, the number of stars involved. For Shetrone et al. (2003) the differences are , , and N = 3; for Koch et al. (2008) they are , , , and N = 6; for Venn et al. (2012) the corresponding values are 113 ± 26 K, 0.08 ± 0.01 dex, −0.07 ± 0.08, and 6; for Lemasle et al. (2012) they are 104 ± 11 K, 0.12 ± 0.03 dex, 0.08 ± 0.04, and 9; and for Fabrizio et al. (2012) they are 7 ± 8 K, 0.10 ± 0.01 dex, 0.33 ± 0.04, and 31. The most significant difference in this comparison is the abundance difference between Fabrizio et al. (2012) and the present work, given the good agreement between their and values with ours. We note for completeness that Fabrizio et al. (2015) reported that their [Fe/H] values are 0.37 dex smaller than those of Venn et al. (2012).
In Figure 6, we compare our [O/Fe], [Na/Fe], [Mg/Fe], and [Ca/Fe] relative abundances (one set in each of the vertical panels) with those of other works for which data are available—Koch et al. (2008) in the leftmost panel, Shetrone et al. (2003) and Venn et al. (2012) together in the next panel, then Lemasle et al. (2012), and finally Fabrizio et al. (2015) in the rightmost panel. Clearly, the agreement is less than ideal. That said, with typical S/N vales of 10–30 and the small number of lines available for the elements in the figure O (1), Na (1), Mg (1–2), and Ca (∼10–15), the results are not unexpected. Examination of the data for Ca, with ∼10–15 lines, where the scatter is smaller, is supportive of this view.
Figure 6. Comparison of the relative abundances (from top to bottom) [O/Fe], [Na/Fe], [Mg/Fe], and [Ca/Fe] of the present work with those (from left to right) of Koch et al. (2008), of Shetrone et al. (2003) and Venn et al. (2012), of Lemasle et al. (2012), and of Fabrizio et al. (2015). The black line is the 1:1 relationship. See text for discussion.
Download figure:
Standard image High-resolution imageIn Figure 6 one also sees that there is larger scatter in the comparison with the abundances of Fabrizio et al. (2015), with a tendency to more supersolar values in the latter. This is a somewhat puzzling result, given that we would have expected the Fabrizio et al. (2012, 2015) values of both [Fe/H] and [X/H] (for element X) to be smaller that ours by similar amounts, and to some extent to cancel out in the relative abundance, [X/Fe]. We also comment that if one considers abundances relative to hydrogen, [X/H], rather than relative abundances [X/Fe], the disagreement seen in Figure 6 is significantly reduced. That is, if we define Δ[X/Fe] = [X/Fe]This work–[X/Fe]Fabrizio and Δ[X/H] = [X/H]This work–[X/H]Fabrizio for O, Na, Mg, and Ca, we find average values , , , and , while in comparison we have , , , and . For all four elements, is closer to 0 than is .
Further work at higher S/N is clearly needed if one is to fully understand the chemical enrichment of Carina.
4. Enlarging the High-resolution Sample from the Literature
We have enlarged the sample in Table 1 by reanalyzing the EWs of high-resolution spectroscopic observations of Carina red giants available in the literature. Our aim is to determine abundances for these stars using, as far as possible, exactly the same techniques as described above, in order to create an enlarged Carina sample with abundances on the same homogeneous system, to provide clearer insight into the detailed abundance profile of the system.
To this end we collated EWs from Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012) in the wavelength range 5300–6780 Å. These works contain data for 5, 9, and 35 Carina giants, respectively. We note that for objects in common with our 32 stars, their EWs are in good agreement with ours (see Section 2.5). In this compilation of 49 data sets there are 18 stars that are also present in our Table 1. In total, there are 63 individual stars in the union of the present work and the literature sample. We refer the reader to our Appendix for the cross-identification of names employed by the various authors for the objects analyzed in the present work.
Basic data for the literature sample are presented in Table 9. Columns (1)–(3) present identification, literature source, and coordinates, respectively; columns (4)–(9) contain V, B − V, I, J, H, and K photometry from the sources discussed in Section 2.3; and in columns (10)–(14) we show our adopted model atmosphere parameters, , its error σ, surface gravity , [M/H], and ξt, determined following the methods described in Section 3 and in Section 4.1 below.
Table 9. Coordinates, Photometry, and Atmospheric Parameters for 49 Carina Red Giants from the Literature
| Object | Sourcea | R.A. (2000) Decl. | V | B − V | I | J | H | K | σTeff | [Fe/H] | ξt | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) |
| Car-484 | 1 | 06 41 39.64 −50 49 58.8 | 17.60 | 1.43 | 16.18 | 15.23 | 14.48 | 14.34 | 4284 | 60 | 0.68 | −1.53 | 2.25 |
| Car-524 | 1 | 06 41 14.71 −50 51 10.1 | 17.62 | 1.31 | 16.29 | 15.37 | 14.75 | 14.59 | 4436 | 71 | 0.79 | −1.72 | 2.50 |
| Car-612 | 1 | 06 40 58.46 −50 53 35.5 | 17.80 | 1.29 | 16.41 | 15.52 | 14.88 | 14.74 | 4437 | 65 | 0.87 | −1.34 | 2.35 |
| Car-705 | 1 | 06 42 17.43 −50 55 55.3 | 17.81 | 1.29 | 16.43 | 15.47 | 14.80 | 14.64 | 4337 | 68 | 0.81 | −1.47 | 2.25 |
| Car-769 | 1 | 06 41 19.70 −50 57 25.6 | 18.01 | 1.21 | 16.71 | 15.74 | 15.14 | 15.02 | 4438 | 93 | 0.95 | −1.64 | 2.30 |
| Car-1013 | 1 | 06 41 21.98 −51 03 43.3 | 17.78 | 1.27 | 16.42 | 15.50 | 14.83 | 14.71 | 4412 | 65 | 0.84 | −1.62 | 2.35 |
| Car-1087 | 1 | 06 41 15.47 −51 01 16.0 | 18.03 | 1.14 | 16.74 | 15.84 | 15.28 | 15.14 | 4542 | 78 | 1.02 | −2.79 | 2.05 |
| Car-5070 | 1 | 06 41 53.85 −50 58 11.2 | 17.88 | 1.21 | 16.53 | 15.62 | 15.04 | 14.90 | 4487 | 80 | 0.93 | −2.24 | 1.80 |
| Car-7002 | 1 | 06 40 49.17 −51 00 33.4 | 18.33 | 0.97 | 17.15 | 16.31 | 15.79 | 15.66 | 4708 | 75 | 1.23 | −2.67 | 2.65 |
| M2 | 2 | 06 41 57.63 −50 59 32.8 | 17.97 | 1.25 | 16.61 | 15.65 | 14.99 | 14.84 | 4359 | 69 | 0.89 | −1.53 | 2.10 |
| M3 | 2 | 06 41 54.60 −50 57 00.9 | 17.67 | 1.49 | 16.10 | 15.06 | 14.44 | 14.27 | 4230 | 116 | 0.67 | −1.79 | 2.35 |
| M4 | 2 | 06 41 48.23 −50 55 01.8 | 17.61 | 1.39 | 16.19 | 15.20 | 14.52 | 14.37 | 4291 | 78 | 0.69 | −1.48 | 2.05 |
| M10 | 2 | 06 41 46.37 −51 01 22.8 | 17.89 | 1.27 | 16.50 | 15.54 | 14.95 | 14.81 | 4411 | 94 | 0.89 | −2.01 | 2.10 |
| M12 | 2 | 06 41 36.49 −50 56 23.3 | 17.88 | 1.29 | 16.53 | 15.53 | 14.90 | 14.74 | 4337 | 89 | 0.84 | −1.32 | 1.90 |
| MKV0397 | 3 | 06 41 58.27 −50 46 41.4 | 18.51 | 1.09 | 17.24 | 16.35 | 15.79 | 15.67 | 4567 | 83 | 1.24 | −2.01 | 2.35 |
| MKV0458 | 3 | 06 41 58.20 −50 48 58.0 | 18.48 | 1.09 | 17.25 | 16.41 | 15.79 | 15.66 | 4586 | 57 | 1.24 | −1.45 | 2.05 |
| MKV0514 | 3 | 06 41 46.00 −50 51 00.6 | 18.17 | 1.24 | 16.89 | 16.01 | 15.41 | 15.27 | 4524 | 62 | 1.07 | −2.05 | 2.20 |
| MKV0556 | 3 | 06 42 22.27 −50 52 09.6 | 19.21 | 0.94 | 18.09 | 17.32 | 16.77 | 16.66 | 4814 | 59 | 1.65 | −1.61 | 1.90 |
| MKV0577 | 3 | 06 41 45.03 −50 52 49.1 | 18.92 | 1.01 | 17.78 | 16.98 | 16.43 | 16.33 | 4766 | 63 | 1.52 | −1.06 | 1.90 |
| MKV0596 | 3 | 06 41 17.69 −50 53 07.8 | 18.51 | 1.09 | 17.30 | 16.47 | 15.89 | 15.78 | 4655 | 62 | 1.29 | −1.57 | 2.05 |
| MKV0614 | 3 | 06 42 37.98 −50 53 38.0 | 18.75 | 1.01 | 17.55 | 16.70 | 16.16 | 16.02 | 4656 | 73 | 1.39 | −1.55 | 2.30 |
| MKV0628 | 3 | 06 40 35.38 −50 54 07.7 | 18.25 | 1.18 | 16.94 | 16.01 | 15.40 | 15.22 | 4429 | 77 | 1.05 | −1.69 | 2.35 |
| MKV0640 | 3 | 06 40 40.84 −50 54 29.3 | 18.32 | 1.20 | 17.06 | 16.12 | 15.55 | 15.38 | 4473 | 87 | 1.10 | −1.85 | 2.50 |
| MKV0652 | 3 | 06 41 40.83 −50 54 45.8 | 18.55 | 1.06 | 17.34 | 16.53 | 15.97 | 15.83 | 4675 | 55 | 1.31 | −2.27 | 2.30 |
| MKV0677 | 3 | 06 40 31.14 −50 55 24.7 | 17.76 | 1.29 | 16.38 | 15.40 | 14.79 | 14.64 | 4372 | 94 | 0.81 | −1.66 | 2.15 |
| MKV0698 | 3 | 06 41 26.12 −50 55 44.0 | 17.60 | 1.38 | 16.18 | 15.18 | 14.50 | 14.34 | 4273 | 80 | 0.68 | −1.29 | 2.25 |
| MKV0708 | 3 | 06 42 38.52 −50 56 00.8 | 18.45 | 1.18 | 17.31 | 16.45 | 15.92 | 15.76 | 4659 | 78 | 1.27 | −1.50 | 2.00 |
| MKV0729 | 3 | 06 42 17.46 −50 56 26.2 | 18.69 | 1.06 | 17.47 | 16.59 | 16.03 | 15.90 | 4600 | 76 | 1.33 | −1.17 | 1.85 |
| MKV0733 | 3 | 06 42 30.38 −50 56 33.2 | 18.78 | 1.04 | 17.55 | 16.67 | 16.15 | 15.99 | 4610 | 93 | 1.37 | −1.19 | 1.95 |
| MKV0740 | 3 | 06 41 29.07 −50 56 46.3 | 18.97 | 1.03 | 17.79 | 16.94 | 16.38 | 16.26 | 4664 | 65 | 1.48 | −0.97 | 2.35 |
| MKV0743 | 3 | 06 41 45.92 −50 56 54.3 | 19.22 | 0.97 | 18.11 | 17.30 | 16.80 | 16.67 | 4803 | 69 | 1.65 | −0.76 | 1.90 |
| MKV0770 | 3 | 06 41 12.30 −50 57 26.1 | 18.33 | 1.04 | 17.13 | 16.25 | 15.69 | 15.57 | 4619 | 76 | 1.19 | −1.49 | 1.80 |
| MKV0780 | 3 | 06 40 57.09 −50 57 44.5 | 18.60 | 1.05 | 17.42 | 16.56 | 16.01 | 15.90 | 4665 | 76 | 1.33 | −1.41 | 2.00 |
| MKV0812 | 3 | 06 40 51.62 −50 58 21.9 | 19.15 | 0.95 | 18.05 | 17.25 | 16.73 | 16.61 | 4810 | 60 | 1.63 | −1.34 | 1.90 |
| MKV0825 | 3 | 06 40 56.96 −50 58 38.4 | 18.11 | 1.20 | 16.81 | 15.89 | 15.28 | 15.13 | 4459 | 74 | 1.01 | −1.30 | 2.25 |
| MKV0840 | 3 | 06 42 02.81 −50 58 59.5 | 18.25 | 1.16 | 16.98 | 16.06 | 15.45 | 15.32 | 4486 | 73 | 1.08 | −1.25 | 1.90 |
| MKV0842 | 3 | 06 40 22.52 −50 59 02.0 | 19.08 | 0.94 | 17.96 | 17.14 | 16.61 | 16.44 | 4726 | 76 | 1.56 | −1.38 | 2.40 |
| MKV0880 | 3 | 06 41 15.67 −50 59 48.1 | 17.83 | 1.32 | 16.43 | 15.44 | 14.77 | 14.62 | 4306 | 78 | 0.79 | −1.52 | 2.20 |
| MKV0900 | 3 | 06 41 27.18 −51 00 18.4 | 17.75 | 1.30 | 16.36 | 15.37 | 14.69 | 14.55 | 4312 | 73 | 0.76 | −1.63 | 1.90 |
| MKV0902 | 3 | 06 41 16.31 −51 00 18.7 | 18.14 | 1.16 | 16.84 | 15.92 | 15.33 | 15.19 | 4486 | 78 | 1.04 | −1.91 | 2.25 |
| MKV0914 | 3 | 06 40 42.49 −51 00 42.7 | 18.26 | 1.10 | 16.98 | 16.07 | 15.55 | 15.39 | 4551 | 99 | 1.12 | −2.07 | 1.95 |
| MKV0916 | 3 | 06 42 08.97 −51 00 48.0 | 18.59 | 1.04 | 17.41 | 16.54 | 15.93 | 15.81 | 4596 | 56 | 1.29 | −1.36 | 2.50 |
| MKV0925 | 3 | 06 40 43.17 −51 01 06.7 | 18.69 | 1.01 | 17.51 | 16.62 | 16.14 | 16.04 | 4702 | 114 | 1.39 | −1.34 | 1.70 |
| MKV0948 | 3 | 06 41 37.66 −51 01 43.8 | 18.00 | 1.23 | 16.64 | 15.71 | 15.14 | 14.97 | 4449 | 91 | 0.96 | −1.94 | 2.20 |
| MKV0976 | 3 | 06 40 57.68 −51 02 40.7 | 18.99 | 0.93 | 17.88 | 17.09 | 16.56 | 16.47 | 4832 | 69 | 1.57 | −1.54 | 2.35 |
| MKV1007 | 3 | 06 41 44.65 −51 03 31.4 | 18.30 | 1.21 | 16.99 | 16.03 | 15.38 | 15.27 | 4408 | 78 | 1.05 | −1.42 | 1.90 |
| MKV1009 | 3 | 06 40 59.29 −51 02 26.7 | 18.14 | 1.15 | 16.87 | 15.98 | 15.38 | 15.23 | 4514 | 68 | 1.06 | −1.52 | 1.75 |
| MKV1012 | 3 | 06 41 00.31 −51 03 43.1 | 18.42 | 1.10 | 17.19 | 16.29 | 15.70 | 15.58 | 4551 | 73 | 1.19 | −1.56 | 2.20 |
| MKV1061 | 3 | 06 41 29.16 −51 05 22.2 | 18.60 | 1.12 | 17.38 | 16.54 | 15.93 | 15.83 | 4618 | 66 | 1.30 | −1.37 | 2.15 |
Note.
aSources: (1) Venn et al. 2012; (2) Shetrone et al. 2003; (3) Lemasle et al. 2012.A machine-readable version of the table is available.
Download table as: DataTypeset image
4.1. Literature Abundance Reanalysis
Abundances of the literature stars were determined by using the procedures outlined in Section 3, for lines in common between our line list and those of the literature sample. There was only one significant difference in the analysis of the literature sample. This was driven by concern about the accuracy of the determination of microturbulence (ξt) resulting from the relatively small number of Fe i lines (∼15–30) available for some stars. In Section 3.2, we determined ξt by requiring that there should be no dependence of abundance on line strength. It became clear in our analysis of the literature data that having only a small number of Fe i lines could lead to significant uncertainty in ξt. As noted above in Section 3.2, an alternative estimate for ξt, used by some workers, is to adopt a generic value of ξt as a function of (e.g., Worley et al. 2013). Insofar as the latter method is independent of the number of Fe i lines and ξt is an artifact of 1D (as opposed to 3D) model atmospheres (Asplund et al. 2000), we investigated this as follows. In addition to determining ξt as described in Section 3.2, we repeated the analysis of the stars in Tables 1 and 9, with ξt defined by ξt = 2.39 − 0.31 × , following Worley et al. (2013). Ideally, the abundances derived by the two methods should give the same results. To investigate how this might depend on the number of Fe i lines available, in Figure 7 we plot Δ[Fe/H], the difference between abundances obtained with the two different prescriptions for ξt, as a function of the number of Fe i lines. It is clear that the scatter increases significantly when the number of Fe i lines is smaller than ∼20. To overcome this problem, in what follows we accepted the abundances determined by using the formulaic value of ξt for the six most discrepant points in Figure 7 (Car-1087, MKV0556, MKV0577, MKV0733, MKV0743, MKV0812 in Table 9); otherwise, we adopted values obtained using ξt as described in Section 3.2.
Figure 7. Difference between [Fe/H] obtained using microturbulence as described in Sections 3.2 and 4.1, as a function of the number of Fe i lines, using data from the present work (star symbols), from Shetrone et al. (2003) and Venn et al. (2012) (circles), and from Lemasle et al. (2012) (triangles).
Download figure:
Standard image High-resolution imageOur abundances for the literature samples are presented in Table 10 for the works of Venn et al. (2012) and Shetrone et al. (2003) and in Table 11 for that of Lemasle et al. (2012). The formatting in these tables is the same as in Table 8.
Table 10. Summarya of [Fe/H], [X/Fe], and Total Errors σTot for 14 Literature (Shetrone et al. 2003; Venn et al. 2012) Carina Red Giants
| Object | [Fe/H] | O | Na | Mg | Al | Si | Ca | Sc | Ti i | Ti ii | V | Cr | Mn | Fe ii | Co | Ni | Cu | Ba | La | Nd | Eu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Car−484 | −1.49 | 0.50 | −0.34 | 0.16 | ⋯ | ⋯ | 0.05 | 0.08 | 0.14 | 0.24 | −0.07 | −0.04 | −0.37 | 0.12 | ⋯ | −0.07 | ⋯ | 0.30 | 0.51 | 0.67 | 0.51 |
| 0.14 | 0.22 | 0.20 | 0.10 | ⋯ | ⋯ | 0.04 | 0.12 | 0.09 | 0.12 | 0.10 | 0.09 | 0.06 | 0.15 | ⋯ | 0.07 | ⋯ | 0.21 | 0.11 | 0.20 | 0.22 | |
| 75 | 1 | 1 | 2 | ⋯ | ⋯ | 20 | 8 | 7 | 4 | 8 | 3 | 6 | 7 | ⋯ | 9 | ⋯ | 1 | 3 | 1 | 1 | |
| Car−524 | −1.73 | 0.47 | ⋯ | 0.25 | ⋯ | 0.41 | −0.01 | −0.02 | 0.07 | 0.03 | −0.03 | −0.05 | −0.37 | 0.17 | ⋯ | −0.02 | ⋯ | 0.19 | 0.61 | 0.44 | ⋯ |
| 0.14 | 0.21 | ⋯ | 0.13 | ⋯ | 0.21 | 0.05 | 0.13 | 0.17 | 0.13 | 0.19 | 0.14 | 0.11 | 0.16 | ⋯ | 0.06 | ⋯ | 0.20 | 0.11 | 0.19 | ⋯ | |
| 64 | 1 | ⋯ | 2 | ⋯ | 1 | 19 | 7 | 2 | 4 | 1 | 3 | 3 | 8 | ⋯ | 6 | ⋯ | 1 | 2 | 1 | ⋯ |
Note.
aFor each object the three rows contain [Fe/H] and [X/Fe], σTot, and the number of lines, respectively.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 11. Summarya of [Fe/H], [X/Fe], and Total Errors σTot for 35 Lemasle et al. (2012) Carina Red Giants
| Object | [Fe/H] | Mg | Ca | Ti i | Ti ii | Cr | Mn | Fe ii | Ni | Ba |
|---|---|---|---|---|---|---|---|---|---|---|
| MKV0397 | −2.02 | ⋯ | 0.44 | ⋯ | 0.21 | −0.62 | ⋯ | 0.24 | ⋯ | −0.88 |
| 0.15 | ⋯ | 0.26 | ⋯ | 0.12 | 0.26 | ⋯ | 0.17 | ⋯ | 0.28 | |
| 17 | ⋯ | 1 | ⋯ | 2 | 1 | ⋯ | 5 | ⋯ | 1 | |
| MKV0458 | −1.47 | 0.07 | 0.33 | 0.31 | 0.33 | −0.17 | −0.48 | 0.40 | 0.47 | 0.27 |
| 0.15 | 0.24 | 0.31 | 0.10 | 0.10 | 0.24 | 0.24 | 0.16 | 0.24 | 0.12 | |
| 26 | 1 | 2 | 3 | 2 | 1 | 1 | 5 | 1 | 2 |
Note.
aFor each object the three rows contain [Fe/H] and [X/Fe], σTot, and the number of lines, respectively.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
5. The ([Fe/H]) Metallicity Distribution Function
An essential observational ingredient that constrains the population characteristics of Carina is its MDF, for which we take the distribution function of [Fe/H] as proxy. We present the MDF for our sample of 63 RGB stars in panel (a) of Figure 8. The mean values and dispersions of the distribution are −1.59 and 0.33 dex (where for the latter we have applied a small correction to take into account the error of 0.15 dex involved in the measurement of [Fe/H]), respectively, while the range in [Fe/H] covers −2.68 to −0.64. For future reference we note that the 63 stars discussed here represent a somewhat incomplete sample of Carina's RGB, due to two effects. First, the four investigations leading to the sample were chosen for high-resolution spectroscopic observations, leading to a bias toward brighter stars (see our Figure 1 and Figure 5 of Paper I). Second, as discussed in Paper I (Section 2.1.1), the sample is probably slightly incomplete at the 5%–10% level, insofar as the RGB distributions of Koch et al. (2006) and Walker et al. (2009a) are slightly broader than that observed for the present sample.
Figure 8. Generalized [Fe/H] metallicity distribution function of Carina based on high-resolution spectroscopy for (a) the sample of 63 RGB stars in the present work and (b) those from Fabrizio et al. (2012) (thick line) and the collective data of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012) (thin line); panel (c) contains results for the RGB sample of Koch et al. (2006) obtained from their analysis of Ca ii IR triplet data, adopting the [Fe/H] calibration of Carretta & Gratton (1997). For these three panels a Gaussian kernel of 0.15 dex, appropriate to the accuracy of the abundance analyses, has been adopted. Panel (d) contains the histogram of the Carina MDF from Starkenburg et al. (2010, their Figure 13) obtained from analysis of the Ca ii IR triplet data of Koch et al. (2006), and panel (e) presents the MDF of Kordopatis et al. (2016, their Figure 7).
Download figure:
Standard image High-resolution imagePanel (b) of Figure 8 presents the MDFs obtained from the results of other high-resolution spectroscopic investigations, where the thin line is based on the collective results of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012), while the thick line comes from the work of Fabrizio et al. (2012) for the 31 stars in common with the present investigation—resulting from independent analysis of the same spectra analyzed in this work (obtained in ESO Proposal 180.B-0806(B); PI: G. Gilmore). We refer the reader to Section 3.4 for a discussion of the differences between the abundances of Fabrizio et al. (2012), on the one hand, and those of the present work and of the collective results of Shetrone et al. (2003), Venn et al. (2012), and Lemasle et al. (2012), on the other. Panels (c) and (d) contain the results of Koch et al. (2006) and Starkenburg et al. (2010), respectively, based on their analysis of measurements of Ca ii IR triplet data. Here one sees that the MDFs derived from the Ca ii data reach somewhat lower abundances than does our analysis. It is unclear whether this is due to selection biases or errors in the application of the CaT calibrations (e.g., errors in the assumed stellar ages). We refer the reader to Paper I (Sections 2.3 and 4), where we have discussed potential shortcomings of the calibrations of the triplet adopted in these publications as applied to Carina. Finally, in panel (e) of Figure 8, we present the MDF of Kordopatis et al. (2016), from their analysis of medium-resolution, near-infrared spectra. For these data the median error of the metallicity is 0.29 dex. We defer further consideration of our MDF to Section 10.
6. Relative Element Abundances
In Figures 9–14 we present relative abundances, [X/Fe], derived in the present work for 18 atomic species in the range O–Eu,14 as a function of [Fe/H]. In each column, the top three panels contain results from analysis of our EWs, from those of Shetrone et al. (2003) and Venn et al. (2012), and from those of Lemasle et al. (2012), respectively. In the bottom two panels, the results for these three subsamples are presented as average values for the 63 independent stars in Tables 8, 10, and 11, as available, weighted by the inverse squares of their total errors. (These average values and their errors may be found in Table 15 of the Appendix.) In these panels, the final uncertainties in the relative abundances are shown in two ways: in the second row from the bottom, the usual error bars are presented, while in the bottom row, the size of the circles decreases linearly as the error increases. The solid red line in each panel represents the mean values for Galactic halo stars, based on the data presented by Venn et al. (2012), which we shall adopt in what follows in our discussion of the abundances of our Carina sample.
Figure 9. [O/Fe], [Na/Fe], and [Mg/Fe] vs. [Fe/H] (left to right). From top to bottom the first three rows contain results for the present sample; from our analysis of data from Shetrone et al. (2003) and Venn et al. (2012); and from our analysis of the data of Lemasle et al. (2012), respectively. The bottom two rows contain the final weighted average values of the data in the top three rows; in the penultimate row total error bars are included; and in the bottom row the size of the symbols decreases linearly as the error increases. The red lines present average values for Milky Way halo stars following Venn et al. (2012).
Download figure:
Standard image High-resolution imageFigure 10. [Si/Fe], [Ca/Fe], and [Sc/Fe] vs. [Fe/H]. The format is as described in Figure 9.
Download figure:
Standard image High-resolution imageFigure 11. [Ti/Fe], [V/Fe], and [Cr/Fe] vs. [Fe/H]. The format is as described in Figure 9.
Download figure:
Standard image High-resolution imageFigure 12. [Mn/Fe], [Fe ii/Fe], and [Co/Fe] vs. [Fe/H]. The format is as described in Figure 9.
Download figure:
Standard image High-resolution imageFigure 13. [Ni/Fe], [Cu/Fe], and [Ba/Fe] vs. [Fe/H]. The format is as described in Figure 9.
Download figure:
Standard image High-resolution imageFigure 14. [La/Fe], [Nd/Fe], and [Eu/Fe] vs. [Fe/H]. The format is as described in Figure 9.
Download figure:
Standard image High-resolution imageIn Figure 15 an alternative summary of the averaged abundances is presented following Yong et al. (2013), in which the results are represented as summed double generalized histogram contour plots having Gaussian kernels equal to the individual total observational errors.
Figure 15. Contours of relative abundance—[X/Fe] vs. [Fe/H]. Here each star is represented by a double Gaussian having kernels equal to the total observational errors. The red lines present average values for Milky Way halo stars following Venn et al. (2012).
Download figure:
Standard image High-resolution imageIn this section we present a brief overview of these results, where in the comparison of Carina's average relative abundances with those of Galactic halo values, the averages will be taken over the range −2.0 [Fe/H] −1.0.
6.1. The Light Elements O and Na
Oxygen and sodium abundances have been determined from only one line each in this analysis (Na i λ5688.2, [O i] λ6300.3; see Table 2). We have selected to restrict our analysis to these lines, which have EW measurements throughout our sample, are known to yield abundances in close accord with other features when these are available, and are in good agreement between various analyses (see, e.g., Venn et al. 2012, Sections 4.4.2 and 4.4.3). Our abundances do not appear to deviate wildly from Galactic halo values, although some stars do show abundances lower than those of the halo by 0.2–0.3 dex, particularly for sodium. As discussed by Venn et al. (2012), the production of sodium follows that of the α-elements until AGB stars contribute, and the latter contributions can be metallicity dependent. Thus, reasonable differences in the mean metallicity of the AGB stars in the Galactic halo versus those in Carina could account for the small differences in some stars.
The mean values, using weights equal to the inverse square of the errors, are and , which may be compared with the Galactic halo values plotted in Figure 9 of 0.60 and 0.00, respectively. As pointed out to us by a referee, if one has low α relative abundances for Mg–Ti in Carina, as seen in our Figures 9–11, one might also expect a significant reduction in oxygen as well. We refer the reader to the work of Ramírez et al. (2012), which confirms the reduction of [O/Fe] in dwarfs of the Galactic halo having [Fe/H] <−0.8 and low relative abundances of the α-elements, Mg–Ti. One might claim that the lower values of [O/Fe] in some of the stars in Figure 9 might offer support for this requirement. That said, we are of the view that further work of considerably higher S/N than available here is needed to resolve this issue.
The most significant result from our data, however, is that there is no strong anticorrelation between the abundances of these two elements, in clear contrast to what is seen in all of the Galactic globular clusters. We shall return to this matter in Section 11.
6.2. The α-elements: Mg, Si, Ca, and Ti
The α-elements are built through He capture during various stages in the evolution of massive stars and dispersed through SN II events. Thus, the [α/Fe] ratio is a key tracer of the relative contributions of SN II to SN Ia products in a star-forming region. As discussed in Venn et al. (2012), Ti is not a true α-element. It behaves, however, like one since the dominant isotope 48Ti forms through explosive Si burning and the α-rich freeze-out during a core-collapse SN event (Woosley & Weaver 1995). In our analysis, we examine 2 lines of Mg i, 3 of Si i, 22 of Ca i, 11 of Ti i, and 5 of Ti ii. Our Ti i and Ti ii abundances are in good agreement when both are measured in the same star, and therefore we average the abundances of the two species. The Mg ii lines near 5200 Å are too strong for the present analysis.
The mean values, using weights equal to the inverse square of the errors, are , , and . With the exception of Si, which is the least accurately measured, all of these fall below halo values (0.30 dex), which is a well-known signature of dSph systems, well documented for Carina by Shetrone et al. (2003) and Venn et al. (2012). We shall discuss this group of elements at some length in Section 7. An interesting effect that we shall emphasize there is that the quality of the data varies strongly between the four elements. Note the clearer tightness of the [Ca/Fe] versus [Fe/H] relationship in Figure 10, in some contrast to the looser ones for the other α-elements—driven, as we shall discuss in Section 7, by the considerably larger number of lines available for Ca in the wavelength range observed in the present investigation.
6.3. The Odd-Z Elements (Sc, V, Mn), Iron-peak Elements (Co, Cr, Ni), and Cu
Massive stars (M > 8 M⊙) provide the first contributions to the chemical elements, due to their short lifetimes, producing metals both during their evolution and during core-collapse SNe. It is currently thought that the iron-peak and odd-Z elements are synthesized in these core-collapse SNe through a variety of processes (explosive burning ranging from He to Si, α-rich freeze-out, a range in yields depending on neutron densities, explosion energies, mass of the progenitor, metallicity and initial composition, and the mass cut for the fraction expelled; see, e.g., Woosley & Weaver 1995; Nomoto et al. 2013; Pignatari et al. 2016). Abundances of these elements tend to show a strong odd–even effect in the predicted yields, where the odd-Z nuclei have lower abundances than those with even Z. Only at later times will lower-mass stars contribute to these elements through SN Ia events, possibly dominating the total iron-group inventory. The diversity of SNe Ia has been modeled by Kobayashi et al. (2015), ranging from single- and double-degenerate channels to rare types from hybrid white dwarfs, as well as their impact in metal-poor systems with stochastic star formation, such as Carina.
In general, our odd-Z elements (Sc, V, Mn) are measured from a small number of spectral lines (1–10) and include hyperfine structure corrections (see Section 3.2). The ranges seen in these abundance ratios are quite large, with Δ[Sc/Fe] and Δ[V/Fe] . The mean values for Sc and V, using weights equal to the inverse square of the errors, are and , while for Mn the value is . In comparison, the corresponding Galactic halo values are 0.10, 0.10, and −0.40. Only tends to be above the Galactic halo data. Kobayashi et al. (2015) have predicted that in inhomogeneously mixed systems, an enhanced [Mn/Fe] value could indicate contributions from SN Iax models (a low-metallicity, hybrid white dwarf, in a close binary system).
Our iron-peak elements Cr and Ni are measured from a small number of lines (4–11) in most of the stars in our sample, and both are in excellent agreement with the Galactic halo trends. The mean values, using weights equal to the inverse square of the errors, are and , which compare well with Galactic halo values of 0.00 and 0.00, respectively. We note that larger dispersions and errors are reported for these elements from the Lemasle et al. data set. Also, a small number of Co and Cu abundances are available for stars from one spectral line each (Co i λ5647.2 and Cu i λ5700.2). Both are limited to the more metal-rich stars in our sample. The [Co/Fe] ratios are in good agreement with the Galactic trend, while the [Cu/Fe] ratios may be slightly below the Galactic halo values. The nucleosynthesis of Cu is more complicated than most of the iron-group and odd-Z elements; for example, Cu can also have a significant contribution from the weak s-process in massive stars (e.g., Pignatari et al. 2016).
6.4. [Fe ii/Fe]
[Fe ii/Fe] provides a necessary and fundamental requirement of any chemical abundance analysis in which it can be determined. That is, a sound analysis should yield [Fe ii/Fe] = 0. Inspection of the middle column of Figure 10 shows that this expectation is not met, with the bulk of [Fe ii/Fe] values lying in the range of 0.0 to +0.5 dex. If one considers the results for the 31 stars plotted in the top panel (for which we presented new observational material and determined abundances in Sections 2 and 3), the mean value, determined using weights equal to the inverse square of the errors, is .
Inspection of Table 7 suggests that this is about two times larger than the uncertainties in the analysis, which are dominated for both elements by the uncertainties in . In the table, one sees that an average error of Δ = −80 K will lead to an error of Δ[Fe ii/Fe] = +0.15.
A second consideration is the overionization of Fe i by the radiation field in the atmosphere of a metal-poor red giant, which is neglected under the assumption of LTE. For the typical stellar parameters of our sample ( = 4500 K, = 1.0, [Fe/H] = −2.0 to −1.0), this effect is estimated to be ≤+0.1 dex (Lind et al. 2012). On the other hand, Mashonkina et al. (2016) find that for Fe i lines with EWs in the range 100–200 mÅ, the effect can be as large as +0.2 dex in the same stellar parameter regime.
Given the magnitude and sign of the NLTE corrections, the LTE Fe i and Fe ii abundances are not anomalous.
6.5. The Heavy-neutron-capture Elements: Ba, La, Nd, Eu
We have determined element abundances for four heavy-neutron-capture elements. These are formed in massive stars and core-collapse SNe through rapid neutron-capture reactions, and those other than Eu also form via slow neutron captures during the thermal pulsing AGB stages in intermediate-mass stars. The specific details of these nucleosynthetic processes are a dynamic field of current research. For the core-collapse SNe, new models and calculations of their yields include details of the SN explosion energies, explosion symmetries, early rotation rates, and metallicity distributions (see, e.g., Kratz et al. 2014; Nishimura et al. 2015; Tsujimoto & Nishimura 2015; Pignatari et al. 2016), as well as exploration of contributions from compact binary mergers as a (or as the most) significant site for the r-process (e.g., see Fryer et al. 2012; Korobkin et al. 2012; Perego et al. 2014; Côté et al. 2017). Similarly, predictive yields from AGB stars by mass, age, metallicity distributions, and details of convective-reactive mixing are also an active field of research (see, e.g., Lugaro et al. 2014; Cristallo et al. 2015; Pignatari et al. 2016).
Our abundances for Ba, La, Nd, and Eu are from only a few lines; for example, Eu ii λ6645.1 and Nd ii λ5319.8 are from only the one line each. Barium and lanthanum are from three and four spectral lines each, respectively, but the Ba ii lines tend to be strong, whereas the La ii lines tend to be weak (or absent). There is a tendency in the relative abundances of these four elements to be similar to or higher than those for stars in the Galactic halo at metallicities [Fe/H] , where the highest abundances tend to occur for [La/Fe] and [Ba/Fe]—in all samples (Shetrone et al. 2003; Lemasle et al. 2012; Venn et al. 2012; this paper). We do not interpret this as due to uncertainties in our abundances but rather to a real astrophysical effect; for example, the bulk of our sample has a full range of [Ba/Fe] ∼ 0.0 to +0.5, with 〈[Ba/Fe]〉 = 0.17 ± 0.02 (weighted by the inverse square of the errors, and where we somewhat arbitrarily exclude the two objects with [Ba/Fe] < −0.50). In comparison, the Galactic halo value is [Ba/Fe] = −0.10. The 1σ offset due to ΔTeff K (see Table 7) leads to an error of Δ[Ba/Fe] = −0.08, which lessens but does not eliminate the offset from the bulk of the Galactic stars. These offsets are similar for La, Nd, and Eu. This abundance signature is typically seen in dwarf galaxies (see Tolstoy et al. 2009) and interpreted in terms of higher yields of Ba (second-peak s-process element, and thus also La and Nd) from metal-poor AGB stars. What is more surprising are the low [Ba/Fe] values (and even two stars with low [Nd/Fe]) at high metallicities. Venn et al. (2012) interpreted this signature in terms of inhomogeneous mixing in the Carina ISM with pockets of iron-rich SN Ia gas. We shall return to this topic in Section 8.
7. The α-elements
The α-elements are of importance for a complete understanding of Carina, given the role they play in the interpretation of its abundance patterns and CMD. Here we address their dependence on metallicity, their relative abundances compared with solar values, their distribution function, and what they have to tell us about the manner in which chemical evolution within the system may have occurred during their ejection from SNe and mixing with the ambient medium to form subsequent generations.
7.1. The -elements as a Function of [Fe/H]
The α-elements comprise O, Ne, Mg, Si, S, Ar, Ca, Ti (e.g., VandenBerg et al. 2006), while in practice in the present work the available elements are O, Mg, Si, Ca, and Ti—with O and Si determined in only a minority of the sample. This leads to a number of complicating factors concerning the comparison between observation and theory, of which we mention two. The first is that given the results of stellar evolution and nucleosynthesis calculations for massive stars (e.g., Woosley & Weaver 1995), the possibility exists that in the metal-poor regime the α-elements might have a nonsolar relative distribution. This leads to the difficulty that stellar evolution isochrone grids that assume scaled-solar α-ratios will be inaccurate at some unknown level. How does one best compare observation with theory? VandenBerg et al. (2015) have argued that since Mg has a greater relative abundance than the other α-elements, it should therefore be a better probe than the other elements (in particular, the more readily and accurately observed Ca) given that it has a greater effect on a star's evolution. The second point is that, in our opinion, only the abundance of Ca is well determined in currently available RGB samples of Carina. This situation is driven by the small numbers of lines available for analysis (on average 1.8, 0.8, 14.6, and 2.5 lines for Mg i, Si i, Ca i, and Ti ii, respectively) and the relatively low S/N (7–23) per 0.03 Å pixel for the majority of stars having full wavelength coverage in the present analysis. Against this background, we seek to address two questions. First, is there evidence for differences in the relative abundances of the α-elements, one from another—in particular, does [Mg/Ca] differ from the solar value of zero? Second, do the α-abundances change as a function of [Fe/H], in both size and dispersion?
As a first approach, we present in Figure 16 two comparisons of light α- and heavy α-elements versus [Fe/H], together with their difference as a function of [Fe/H], based on the data presented in Figures 9–14. The top panels of each column contain light α-elements, while the middle panels present heavy ones. The bottom panels show the difference between the light and heavy species. One sees that, below [Fe/H] =−1.2, on average the difference between the two species is not large, of order 0.1 dex, with a hint of a dependence on [Fe/H]. For the complete Carina sample in the bottom right panel, . It will be interesting to see whether data of higher quality support these results.
Figure 16. [α-related indices/Fe] vs. [Fe/H]. Left: In the top panel is the average of the light α-elements O, Mg, and Si, in the middle it is the average of the heavy α-elements Ca and Ti, and the bottom panel presents the difference between the mean light and heavy α-elements presented in the top and middle panels. Right: same format as in the left panels, but for the light α-element, Mg, and the heavy α-element, Ca. See text for discussion.
Download figure:
Standard image High-resolution imageA fundamental result of abundance studies of the dSph galaxies is that the α-elements exhibit a very different behavior with respect to [Fe/H], when compared with that found in Galactic halo stars. That is, while the latter exhibit relatively constant and enhanced values of [α/Fe] for [Fe/H] < −1.0, which decrease to ∼0.0 as [Fe/H] decreases to 0.0, for dSph systems the decrease of the α-elements to solar values begins at much lower values of [Fe/H] to −2.0 (see, e.g., Tolstoy et al. 2009). This behavior is understood in terms of different rates of star formation between the two types of systems, in which the dwarf galaxies have lower star formation rates and SNe Ia play a larger role at lower [Fe/H] in reducing [α/Fe] than occurred in the Galactic halo (see, e.g., Gilmore & Wyse 1991). In Carina, the present data suggest that on average the abundance of the α-elements, in particular that of the most accurately measured element, Ca, is lower than Galactic halo values by ∼0.2 dex at all values of [Fe/H], below . We shall return to this in Section 7.3.
7.2. The [α/Fe] Distribution Function
A second fundamental relationship involving [α/Fe] is its distribution function, and of considerable importance is the comparison of the Carina distribution with that of the Galactic halo. In Figure 17 we present [α/Fe] values for Mg, Si, Ca, and Ti determined for the Galactic halo, Carina, and the globular cluster ω Cen. (We include ω Cen insofar as it may be of interest given that it is a Galactic globular cluster of baryonic mass 4.0 M⊙ [D'Souza & Rix 2013], similar to that of Carina, and which has chemically enriched itself not only in the light elements but also in iron.) See the figure caption for sample details. We caution that while individual studies might be internally consistent, there are likely to be small zero-point offsets between the various works. The format of Figure 17 is similar to that of Figure 16, and the top four panels in each column present results for Mg, Si, Ca, and Ti, taken from sources listed in the figure caption, while in the bottom panel the value of [α/Fe] is determined by averaging [Mg i/Fe], [Ca i/Fe], and [Ti ii/Fe] when all three quantities are available. In the interest of obtaining the most reliable result for Carina, we have required that a value only be accepted when a star has no fewer than two lines available for each element, and we have weighted the individual abundances by the inverse square of their errors. (We made exceptions for three stars, Car-1087, Car-5070, and Car-7002, which have only one line of Mg and/or Ti but the highest S/N [∼30] in the sample.) The data for the 30 Carina giants that meet these criteria are presented in Table 12 and were used to determine the [α/Fe] distribution function presented in the bottom panel of Figure 18, where the thick red line is based on the means of Mg, Ca, and Ti determined by using weights inversely proportional to the inverse square errors in abundance, while the thin black line presents results when equal weights are assumed. In the top panel the distribution function is presented for the Galactic halo (over the range −3.0 < [Fe/H] < −1.0).
Figure 17. Comparison of [α/Fe] abundances for the Galactic halo (data from Fulbright 2000; Preston & Sneden 2000; Barklem et al. 2005; Yong et al. 2013; left panels); Carina (this work; middle panels), where the size of the symbols decreases linearly as the error increases; and ω Cen (Norris & Da Costa 1995; right panels).
Download figure:
Standard image High-resolution imageFigure 18. Carina [α/Fe] distribution function, based on stars for which abundances are available for all of Mg, Ca, and Ti. The thick red line represents average abundances that are the weighted means using weights inversely proportional to the inverse square errors, while the thin black line results when equal weights are assumed. In the top panel the result is presented for the Galactic halo. Here the data have been taken from the samples listed in the caption to Figure 17. A Gaussian kernel of 0.10 dex has been adopted in preparing the diagram. Note that the results for Carina's [α/Fe] are sensitive to the weighting procedure at only the ∼0.1 dex level, and also that there is an [α/Fe] ∼ 0.25 dex offset between the Carina (when error-dependent weights are adopted) and Galactic halo samples.
Download figure:
Standard image High-resolution imageTable 12. [α/Fe] Values and Errorsa for 30 Carina Red Giants
| Name 1 | Name2 | [Fe/H] | σFe | [Mg/Fe] | σMg | [Si/Fe] | σSi | [Ca/Fe] | σCa | [Ti/Fe] | σTi | [α/Fe] | σ[α/Fe] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) |
| CC06122 | Car-484 | −1.46 | 0.10 | 0.20 | 0.09 | 0.21 | 0.22 | 0.07 | 0.03 | 0.29 | 0.09 | 0.099 | 0.026 |
| CC06975 | −1.84 | 0.14 | 0.27 | 0.05 | ⋯ | ⋯ | 0.14 | 0.06 | 0.17 | 0.18 | 0.215 | 0.038 | |
| CC07452 | Car-612 | −1.33 | 0.10 | −0.45 | 0.11 | ⋯ | ⋯ | −0.27 | 0.03 | −0.16 | 0.09 | −0.272 | 0.030 |
| CC08447 | −1.48 | 0.13 | 0.28 | 0.23 | 0.10 | 0.22 | 0.08 | 0.04 | 0.55 | 0.13 | 0.125 | 0.038 | |
| CC08469 | Car-705 | −1.43 | 0.10 | 0.00 | 0.07 | 0.42 | 0.16 | 0.04 | 0.03 | 0.16 | 0.10 | 0.037 | 0.025 |
| CC08615 | −1.73 | 0.11 | 0.52 | 0.24 | 0.56 | 0.24 | 0.18 | 0.05 | 0.05 | 0.25 | 0.189 | 0.048 | |
| CC08695 | M12 | −1.32 | 0.10 | 0.16 | 0.10 | 0.14 | 0.22 | 0.03 | 0.04 | 0.26 | 0.10 | 0.069 | 0.034 |
| CC08788 | −1.48 | 0.13 | 0.26 | 0.14 | 0.06 | 0.24 | 0.14 | 0.07 | 0.05 | 0.10 | 0.132 | 0.053 | |
| CC09000 | M3 | −1.81 | 0.10 | −0.31 | 0.05 | ⋯ | ⋯ | −0.22 | 0.03 | 0.28 | 0.10 | −0.210 | 0.024 |
| CC09179 | −1.78 | 0.15 | 0.03 | 0.38 | 0.84 | 0.24 | −0.14 | 0.08 | −0.08 | 0.12 | −0.117 | 0.066 | |
| CC09225 | Car-769 | −1.65 | 0.10 | 0.38 | 0.06 | 0.28 | 0.16 | 0.10 | 0.05 | 0.39 | 0.12 | 0.243 | 0.035 |
| CC09226 | −1.56 | 0.13 | 0.18 | 0.15 | 0.34 | 0.29 | 0.11 | 0.06 | 0.24 | 0.18 | 0.130 | 0.053 | |
| CC09430 | −2.13 | 0.15 | 0.75 | 0.22 | ⋯ | ⋯ | 0.14 | 0.09 | 0.37 | 0.21 | 0.247 | 0.077 | |
| CC09633 | Car-5070 | −2.24 | 0.11 | −0.17 | 0.17 | ⋯ | ⋯ | 0.01 | 0.07 | 0.03 | 0.14 | −0.003 | 0.058 |
| CC09869 | −1.26 | 0.15 | 0.19 | 0.04 | 0.13 | 0.14 | 0.06 | 0.06 | 0.29 | 0.23 | 0.153 | 0.033 | |
| CC09929 | −1.50 | 0.15 | 0.16 | 0.08 | 0.21 | 0.26 | 0.24 | 0.08 | 0.21 | 0.17 | 0.201 | 0.054 | |
| CC10038 | −1.30 | 0.15 | 0.24 | 0.25 | 0.33 | 0.18 | −0.02 | 0.08 | 0.35 | 0.17 | 0.062 | 0.070 | |
| CC10194 | −1.42 | 0.15 | 0.15 | 0.14 | 0.18 | 0.27 | 0.01 | 0.08 | 0.23 | 0.16 | 0.074 | 0.064 | |
| CC10318 | M2 | −1.53 | 0.10 | 0.15 | 0.05 | 0.31 | 0.16 | 0.06 | 0.04 | 0.33 | 0.09 | 0.114 | 0.029 |
| CC10414 | −1.35 | 0.14 | 0.10 | 0.25 | 0.29 | 0.14 | 0.12 | 0.07 | 0.04 | 0.12 | 0.100 | 0.059 | |
| CC10686 | −1.68 | 0.13 | 0.30 | 0.19 | 0.24 | 0.21 | 0.07 | 0.03 | 0.32 | 0.16 | 0.084 | 0.029 | |
| CC10944 | −1.89 | 0.12 | 0.26 | 0.13 | 0.44 | 0.24 | 0.06 | 0.06 | 0.21 | 0.22 | 0.102 | 0.053 | |
| CC11217 | −1.28 | 0.14 | 0.09 | 0.12 | 0.11 | 0.15 | 0.04 | 0.04 | 0.36 | 0.11 | 0.079 | 0.036 | |
| CC11560 | −1.60 | 0.14 | 0.03 | 0.11 | ⋯ | ⋯ | 0.15 | 0.04 | 0.05 | 0.10 | 0.125 | 0.035 | |
| CC12039 | Car-1013 | −1.56 | 0.09 | 0.18 | 0.06 | 0.22 | 0.17 | −0.02 | 0.04 | 0.36 | 0.13 | 0.063 | 0.031 |
| Car-524 | −1.73 | 0.14 | 0.25 | 0.13 | 0.41 | 0.21 | −0.01 | 0.05 | 0.03 | 0.13 | 0.024 | 0.044 | |
| Car-1087 | −2.47 | 0.16 | 0.15 | 0.26 | ⋯ | ⋯ | −0.45 | 0.15 | 0.53 | 0.28 | −0.153 | 0.118 | |
| Car-7002 | −2.68 | 0.15 | −0.01 | 0.23 | ⋯ | ⋯ | −0.02 | 0.11 | 0.45 | 0.23 | 0.055 | 0.091 | |
| M4 | −1.49 | 0.14 | 0.20 | 0.17 | 0.11 | 0.18 | 0.04 | 0.04 | 0.25 | 0.10 | 0.075 | 0.036 | |
| M10 | −1.99 | 0.14 | 0.01 | 0.09 | ⋯ | ⋯ | −0.10 | 0.05 | 0.03 | 0.10 | −0.057 | 0.040 |
Note.
aThe errors appear in the columns following the abundances, and the column header σMg (for example) stands for σ[Mg/Fe].A machine-readable version of the table is available.
Download table as: DataTypeset image
We make the following points concerning Figures 17 and 18: (i) As noted above, for Carina, our spectroscopic [α/Fe] distribution is determined in large part by that of Ca, given the higher precision of the [Ca/Fe] values. That being said, the lower accuracy of Mg and Ti causes the two distributions in Figure 18 to be offset by only Δ[α/Fe] ∼ 0.05 dex. (ii) The weighted [α/Fe] distribution for Carina is smaller by ∼0.25 dex than that of the Galactic halo. As noted above, the Galactic halo data come from a number of studies and could be affected by zero-point offsets. Inspection of the four halo data sets (Fulbright 2000; Preston & Sneden 2000; Barklem et al. 2005; Yong et al. 2013) plotted in the left panel of Figure 17, however, suggests that this is not the case insofar as each of them has ∼ 0.3. (iii) In Carina, the observed spread in [α/Fe] is small, with dispersion 0.13 ± 0.02 dex. (iv) While the number of stars is not large at lowest abundance, for [Fe/H] < −2.0 one finds , which is small compared with the higher values of [α/Fe] that one associates with the Galactic halo (i.e., [α/Fe] ). (v) While more data are required, there appear to be stars with low values of [α/Fe] over the entire range −2.0 < [Fe/H] < −1.0 (where some 80% of the sample lies).
The final two points are of considerable importance. If point (iv) obtains, the absence of Galactic-halo-like [α/Fe] values ([α/Fe] ) on the RGB would suggest that all of the Carina stars currently observed to date at high resolution formed from material enriched by ejecta from either SNe Ia (e.g., Tolstoy et al. 2009, and references therein) or SNe II in a population having a mass function skewed toward lowest masses (e.g., Kobayashi et al. 2006; Kobayashi & Nakasato 2011), both of which lead to lower [α/Fe] values in subsequent generations. We shall return to point (v) in the next subsection.
The improved data presented in this section may also be used to readdress the question of the dependence of [α/Fe] on atomic species discussed in Section 7.1. Figure 19 presents the dependence of [Mg/Ca] on [Fe/H] for the Galactic halo and Carina, for the samples discussed in the present section and defined in Figure 17, for stars for which both Mg and Ca abundances are available. As noted above, this Carina sample contains only 30 stars, with somewhat conservative selection criteria, and as such might be expected to be of higher quality than the results discussed in Section 7.1. The result in the right panel of Figure 19 leads essentially to the same conclusion as reported in Section 7.1: the difference between the [Mg/Fe] and [Ca/Fe] distributions of Carina is essentially the same, with a mean value of . For the halo sample in Figure 19 the mean value is .
Figure 19. Comparison of the relative magnesium-to-calcium ratio, [Mg/Ca], as a function of [Fe/H] for the Galactic halo (data from Fulbright 2000; Preston & Sneden 2000; Barklem et al. 2005; Yong et al. 2013; left panel) and Carina (right panel).
Download figure:
Standard image High-resolution image7.3. Incomplete Mixing
We complete this section with a comment on the asymmetry of the [α/Fe] distribution function seen in Figure 18 and the distribution of stars in the ([Ca/Fe], [Fe/H])–plane, where we use [Ca/Fe] as proxy for [α/Fe], recalling that Ca has the most accurately determined abundances among the α-elements. The main point is that the asymmetry of the [α/Fe] distribution function to smaller values of [α/Fe] in Figure 18 is clear. To investigate this further, in Figure 20, in the top panel, we reproduce the [Ca/Fe] results from Figure 10 (second panel from the bottom), and in the bottom panel we present only the higher-quality data in the sample that have errors σ[Ca/Fe] < 0.15. As noted in the previous section (point (v)) and seen more clearly in the bottom panel, there are stars with low values of [Ca/Fe] (i.e., below ∼0.0 dex) at all values of [Fe/H], most significantly in the range −2.0 < [Fe/H] < −1.0, where the density of points is highest. While more and better data are needed, the existence of low [Ca/Fe] values at all [Fe/H] drives the asymmetry of the [α/Fe] distribution function at all values of [Fe/H] and is very likely indicative of inhomogeneous mixing of the ejecta of SNe within each of Carina's generations, between the relatively α-element-poor ejecta from SNe Ia and the ambient medium during the several formation epochs of Carina's populations.
Figure 20. [Ca/Fe] vs. [Fe/H] for the Carina RGB stars of the present investigation. In the top panel all stars are plotted, while in the bottom panel only those with σ[Ca/Fe] < 0.15 are presented, permitting clearer insight into the [Ca/Fe] distribution. See text for discussion.
Download figure:
Standard image High-resolution image8. The SN Ia Enrichment of Carina
Venn et al. (2012) first demonstrated quite generally that Carina exhibits enrichment by SNe Ia. In particular, their star Car-612, with [Fe/H] = −1.3, exhibits element deficiencies of Δ[X/Fe] ∼ 0.7 for all elements other than those in the Fe peak, relative to Galactic halo stars having the same [Fe/H]. They interpret this result in terms of Car-612 having formed from material that was substantially enriched by the ejecta of SNe Ia that contained principally Fe-rich material. We have adapted the formalism of their Section 5.4 to search for similar stars in the present sample. For each star we determined Δ[Xi/Fe] = [Xi/Fe]Carina – [Xi/Fe], where [Xi/Fe]Halo is the value determined at the observed [Fe/H] and obtained using the halo averages of Venn et al. (2012) (and plotted in our Figures 9–15). We then compared these with the SN Ia and SN II models of Iwamoto et al. (1999) as follows. For each of the seven Iwamoto et al. (1999) Type Ia models we created a set of admixtures of Type Ia and Type II models, similar to that which one might envisage having formed in Carina as the ejecta of SNe Ia appeared in the system. Then for each admixture we computed the abundance difference Δ[Xi/Fe]Model = [Xi/Fe] – [Xi/Fe]Type II. For each Iwamoto et al. model admixture we then determined the summation S = [Xi/Fe]Carina –Δ[X/Fe], for the set of elements i = O, Na, Mg, Si, Ca, Ti, V, Cr, Mn, Co, and Ni, and accepted the admixture having the smallest S as representing the best model for the star in question.
Figure 21 shows an example of the process for the Venn et al. (2012) star Car-612 (CC07452 in our Table 1). Here each cell represents a comparison of the observations with the model admixture described in the legend of that cell, where the abscissa is atomic number and the ordinate represents the difference between the abundance of the admixture and that of Type II material, for both observation and theory. Each of the seven columns pertains to one of the Iwamoto et al. (1999) models, and for a given column the fraction of Type Ia material increases from zero Type Ia material in the bottom cell to an admixture of 0.6 Type Ia plus 0.4 Type II material at the top. In the case of Car-612 the best fit occurs for the Iwamoto et al. (1999) W70 Type Ia for an admixture of 0.4 Type Ia + 0.6 Type II material, which is presented in blue in the second column from the left and the third row from the top.
Figure 21. Comparison of model admixtures of SNe Ia and SNe II (small black dots) and observed abundances (red filled circles) as a function of atomic number for Car-612 = CC07452. For the model, the ordinate is Δ[Xi/Fe] = [Xi/Fe] – [Xi/Fe], while for the observations it is Δ[Xi/Fe] =[X/Fe]Carina – [Xi/Fe]Halo. Blue symbols are used for the best-fit case. The size of the observational symbols decreases linearly as the error increases. See the text for more details.
Download figure:
Standard image High-resolution imageThe results of this exercise for the 63 red giants are presented in Table 13, where columns (1)–(3) contain the star name, the Iwamoto et al. (1999) Type Ia model admixed in the best-fitting model, and the fraction of Type Ia material involved. For seven stars, which we identify in the table, abundances are available for only 4 of the 11 elements that we include in the above analysis, which leads to less accurate and inconclusive results, and we do not consider these further here.
Table 13. Fraction of Type Ia Material, , and [Ba/Fe] in the Carina Red Giants
| Star | Iwamoto Typea | Type Ia Fraction | Δ[Ba/Fe] | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| MKV0842 | Type II | 0.00 | −0.07 | −0.54 |
| CC10194 | WDD3 | 0.06 | −0.19 | 0.25 |
| MKV0677 | Type II | 0.02 | −0.10 | 0.05 |
| MKV0628 | Type II | 0.02 | −0.12 | 0.03 |
| MKV0640 | WDD1 | 0.06 | −0.02 | 0.44 |
| MKV0914 | Type II | 0.02 | −0.12 | −0.29 |
| MKV0925 | Type II | 0.00 | 0.28 | 0.19 |
| Car-7002b | ⋯ | ⋯ | ⋯ | ⋯ |
Notes.
aAdmixed Iwamoto et al. (1999) Type Ia SN. "Type II" implies zero Type Ia. bInsufficient information: too few elements observable.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
The present formalism differs from that of Venn et al. (2012) insofar as the analysis of Iwamoto et al. (1999) includes no species past the iron peak, while Venn et al. (2012) also include heavy-neutron-capture elements. To investigate the possible significance of this, we extend the analysis to include barium and compute the mean difference, Δ[Xi/Fe], between the relative abundance [Xi/Fe] and [Xi/Fe]Halo (weighed by the inverse square of the errors) for the non-iron-peak elements O, Na, Mg, Si, Ca, Ti, and Ba. The resulting values and Δ[Ba/Fe] are presented in columns (4) and (5) of Table 13.
Figure 22 shows generalized histograms of the logarithm of the Type Ia fractions (Fraction) and . In the left and right panels one sees that the bulk of the stars fall within the ranges 0.0–0.2 and −0.3–0.0, respectively, and in both panels there are a few objects above and below these ranges, respectively. The latter objects are the stars that show the characteristics of Type Ia enrichment.15
Figure 22. Histograms of the logarithm of Fraction(left) and (right) of the Carina red giants analyzed in this work, where a Gaussian kernel of 0.008 has been adopted in both cases, to facilitate identification of individual stars.
Download figure:
Standard image High-resolution imageIn order to proceed with the discussion, we identify Type Ia enriched objects as those in which (i) the average of Fraction and is greater than 0.20 and (ii) Δ[Ba/Fe] = [Ba/Fe]Carina – [Ba/Fe] < 0.0 (if data are available). There are seven objects that meet these requirements; for six of these we plot in Figure 23 (left panels) the abundances relative to those of the Galactic halo, Δ[Xi/Fe] (=[X/Fe]Carina – [Xi/Fe]Halo), as a function of atomic number. We also plot as a line the best-fitting admixed Iwamoto model described above. We note for completeness that CC07452 and CC96633 were first described by Venn et al. (2012) as having been formed from material that had been enriched by ejecta from SNe Ia. MKV0740 and MKV0743 were first analyzed by Lemasle et al. (2012). It will be interesting to see whether future observations support our identification of them as Type Ia enriched. Our seventh candidate, Car-1087, is shown in the top right panel. Given the high value of Δ[Mg/Fe] in this star, we are reluctant to identify it as Type Ia enriched. For completeness, the remainder of the right panels in the figure contains stars that show little if any evidence for Type Ia enrichment.
Figure 23. Δ[Xi/Fe] as a function of atomic number. Left panels: comparison of the best-fit Iwamoto et al. Type II and Type Ia admixture models (black line) with observations (red circles; size of the symbols decreases linearly as the error increases) of the six Carina giants that show the strongest evidence for Type Ia enhancement. For the model, the ordinate is Δ[Xi/Fe] = [Xi/Fe]Admixture – [Xi/Fe], while for the observations it is Δ[Xi/Fe] = [Xi/Fe]Carina – [Xi/Fe]Halo. Right panels: the top panel shows a seventh Type Ia enhanced candidate, which we reject as inconclusive. The other five stars present abundances typical of Carina red giants with no Type Ia enhancement.
Download figure:
Standard image High-resolution imageIf the six stars in the left panels of Figure 23 are indeed all Type Ia enriched, this would suggest that some 10% of the 56 members of the Carina RGB sample presented in Table 13 have this property. While the statistics available for the Galactic halo are small, the Carina fraction appears large compared with the 1%–2% reported as Galactic halo "Fe-enhanced" stars by Yong et al. (2013) (who used the same analysis techniques as adopted here).
9. Age Estimates
The location of the RGB in the CMD (or alternatively in the luminosity−effective temperature plane) is principally determined by [Fe/H], age, and to a lesser extent [α/Fe] and helium. For representative Carina giants in the present sample, with [Fe/H]/[α/Fe]/Age = −1.50/0.0/7.0 and absolute magnitude MV = −1.5, for example, uncertainties in and [Fe/H] of 50 K and 0.1 dex each lead to age differences of ∼3 Gyr.
There are also, as we shall see, intriguing age differences of the same order between different stellar evolution modeling formalisms. It is thus well appreciated that this is not the place to anticipate accurate age determinations. This caveat notwithstanding, in this section we shall investigate what may be learned from determining ages from our current , [Fe/H], and [α/Fe], interpreted using currently available isochrones. A further uncertainty in these assumptions lies in our choice of [α/Fe]. Following the discussion in Section 7.2, we recall that our values of [α/Fe] are determined principally by [Ca/Fe], given the greater relative accuracy with which the determination could be made. As noted there, this value differs by only ∼0.08 dex from that obtained for [Mg/Fe].
With our MV, , [Fe/H], and [α/Fe] (using [Ca/Fe]) we have interpolated in the Yale–Yonsei (Demarque et al. 2004),16 Victoria–Regina (VandenBerg et al. 2006),17 and Dartmouth (Dotter et al. 2008)18 isochrones, assuming that all of our stars lie on the RGB and have ages in the range of 2–14 Gyr. In the cases where extrapolation in age is required we have adopted a value of 2 or 14 Gyr, as appropriate.
The comparison between the ages for the three sets of isochrones is shown in Figure 24, where the three panels show the various combinations. The strong sensitivity of age to the modeling assumptions is clear, and lest one might conclude that the better agreement between Yale–Yonsei and Dartmouth is indicative of superiority, we recall that these two formalisms originate from a common source. Another estimate of the age uncertainties may be obtained by comparing the present values with those of Lemasle et al. (2012), who have provided ages of Carina red giants based on the isochrones of Pietrinferni et al. (2004, 2006). Here, by way of example, we compare our ages obtained using the Dartmouth isochrones with the results of Lemasle et al. (2012) and investigate the mean differences in age, ΔAge (in the sense Age – Age), for stars in common between the two investigations with neither involving extrapolation in the age determination. We find a mean difference and an age dispersion of σ(ΔAge) = 3.3 ± 0.4 Gyr. This dispersion is of the same order as might have been expected from the above discussion.
Figure 24. Comparison of the ages of the red giants of Carina determined using the isochrones of Demarque et al. (2004) (Yale–Yonsei), VandenBerg et al. (2006) (Victoria–Regina), and Dotter et al. (2008) (Dartmouth). The diagram demonstrates the difficulty in age determination for red giants from analysis of their position in the CMD, resulting from the relatively small sensitivity of age to temperature and abundance and small differences between the different stellar isochrones.
Download figure:
Standard image High-resolution imageIn Figure 25, the left panel presents the generalized histograms of age for the three isochrone sets (obtained using a Gaussian kernel with σ = 3.0 Gyr). The best that may be said of this diagram is that two main groupings are evident: one that is old, and the other young and in the range of Gyr.19 For comparison, in the right panel of the figure, we present a generalized histogram (obtained with the same Gaussian kernel) based on the variable [α/Fe] population model in Paper I, where we used synthetic CMD techniques that led to four components for Carina, described in the legend in the figure in terms of the [Fe/H]/[α/Fe]/Age parameters of the populations. The four components are distinguished in the diagram. One would have to say that the agreement between the two panels is at best indicative, driven (as noted above) by the large errors associated with the determination of ages based on the positions of red giants in the CMD.
Figure 25. Left: generalized histograms of the age distributions of the Yale–Yonsei (blue), Victoria–Regina (green), and Dartmouth (red) isochrones. The three distributions have been normalized to have the same area. Right: histogram of the age distribution of a four-component model of Carina based on Paper I, for which the population parameters are given in the legend. Red, green, blue, and magenta refer to first through fourth populations, respectively, while their summation is presented in black. A Gaussian kernel having σ = 3.0 Gyr has been adopted in both panels.
Download figure:
Standard image High-resolution imageFinally, Figure 26 presents the age–metallicity relationship (AMR) for Carina. On the left, Dartmouth ages20 are plotted as a function of [Fe/H], where the size of the symbols increases as their [Ca/Fe] values decrease. The first thing to note about this panel is that for abundances [Fe/H] < −1.8, all stars appear to have ages of 14 Gyr. This is of no physical significance, since, as stated above, when upward extrapolation in the age was required, we set an upper limit of 14 Gyr. That said, in this panel one sees evidence for Type Ia enrichment (decreasing [Ca/Fe]) not only at all [Fe/H], as discussed in Section 8, but also at all ages. The right panel presents the relationship for the four populations determined in our synthetic CMD analysis for the variable [α/Fe] case presented in Paper I, where the bars represent the ranges in age and metallicity of the populations. The form of Carina's AMR is of considerable interest. Both determinations in Figure 26 show that the oldest population, including Carina's metal-poor pre-enrichment tail, brought Carina's metallicity up to [Fe/H] ∼ −1.5 dex, and that gas must have been retained for the following star formation, given that the younger populations join smoothly in metallicity (and, importantly, element ratios) to the older ones. It follows that the ensuing two-thirds of star formation managed to regulate itself against gas loss in such a way that very little net extra chemical enrichment occurred. We conjecture that star formation was self-limiting against gas winds over almost the whole of Carina's star-forming duration.
Figure 26. AMR for Carina. Left: age vs. [Fe/H] for 63 RGB members, where the size of the symbols increases as their [Ca/Fe] values decrease. Right: data for the four CMD populations (variable [α/Fe] case) discussed in Paper I, where the bars represent the [Fe/H] and age spreads determined in that work. The population parameters are given in the legend.
Download figure:
Standard image High-resolution image10. Comparison between Observed and Synthetic CMD Metallicity and [α/Fe] Distribution Functions
In Paper I and the present work we have determined Carina's MDF and [α/Fe] distribution function using two very different and basically independent methods. Paper I presented an analysis of the CMD in terms of synthetic CMDs based on the fitting of isochrones to the observations, while in the present work this has been achieved by the analysis of high-resolution, moderate-S/N spectra of its red giants. A comparison of the results is presented in Figure 27, where the thick (red) and thin (black) lines refer to the present spectroscopic results and the CMD analysis of Paper I, respectively. The MDFs appear on the left and the [α/Fe] distribution function on the right, while the top and bottom panels present results pertaining to the synthetic CMD analysis when [α/Fe] is allowed to vary and when it is held constant, respectively. Finally, the values in the upper right corner of the panels contain the defining physical parameters [Fe/H]/[α/Fe]/Age of the four populations that were determined in the CMD analysis of Paper I. We recall here that in Paper I we referred to these four groups in terms of increasing age as the "first," "second," "third," and "fourth" populations. We shall adopt this nomenclature in what follows. In each panel the areas under the two distributions have been normalized to be equal.
Figure 27. Comparison between the observed (thick red) and synthetic (thin black) ([Fe/H]) MDF and [α/Fe] distribution functions of the Carina upper RGB, for variable [α/Fe] (top panels) and fixed [α/Fe] (bottom panels). Gaussian kernels having σ values of 0.15 and 0.10 dex were used for the [Fe/H] and [α/Fe] distributions, respectively. The synthetic CMD population parameters are given in the upper right corner of the panels.
Download figure:
Standard image High-resolution imageWhile the fits are not outstanding, they show basic agreement between the two methods. Consider first the [α/Fe] distribution function. As might have been expected, given the observed variations in the abundances of the α-elements, the variable-α case (top right panel) provides a better and reasonable fit, except for the asymmetry of the observations to lower values of [α/Fe], which is not included in the models. As discussed in Section 7.3, we regard this as evidence of incomplete mixing of the ejecta from SNe Ia with the ambient medium during the formation of Carina's populations.
The fits of the MDFs are found wanting in three areas: the observations show a small offset to lower abundance, an asymmetry favoring lower abundances, and a somewhat broader distribution. Given the possibility that the RGB sample is incomplete and the likelihood that there are small differences between the abundance scales of the stellar atmosphere and stellar evolution formalisms, among other possibilities, the agreement could have been worse.
10.1. The Need for a More Complicated "First" Population
In Section 5 of Paper I, we discussed the shortcoming of our first population in that while we described it as monomodal with mean metallicity [Fe/H] = −1.85 and with very little spread (Δ[Fe/H] ∼ 0.1), there are in the literature high-resolution spectroscopic abundance analyses of some five Carina red giants with abundances in the range −2.9 < [Fe/H] −2.5. The present work essentially confirms this result: while in our Table 15 there is only one star with [Fe/H] < −2.5, there are eight with [Fe/H] < −2.0. Of these, three are also present in the literature sample with −2.9 < [Fe/H] −2.5.
In Paper I we determined a mean age and metallicity for each of the four populations, with which we associated spreads in age and metallicity. As discussed there, however, given available information, these spreads were not well constrained. There are a number of possible explanations for the absence of stars with [Fe/H] < −2.0 in our model. One is that our first population is multimodal, and that in Paper I we essentially identified only a major subcomponent of the oldest population, while there exists a more metal-poor, presumably older and minor subcomponent as well.21 While this is outside the scope of the present work and we shall not consider it further, it is tempting to conjecture that this minor component contains the first stars to form in Carina. Other, more detailed possibilities include simple inhomogeneous mixing of the early star-forming gas (e.g., Revaz & Jablonka 2012) and/or active accretion of lower-mass systems in the earliest stages of Carina's formation, such as described by the models of Wise et al. (2012).
11. A Search for the [Na/Fe] versus [O/Fe] Anticorrelation
It has become clear in the past three decades that all Galactic globular clusters exhibit strong and anticorrelated abundance variations within the light elements C, N, O, Na, Mg, and Al (Gratton et al. 2004, and references therein). Indeed, the effect is so ubiquitous and strong that Carretta et al. (2010) have suggested, based on their study of the Na–O anticorrelation in some 17 clusters, "a new definition of bona fide globular clusters[,] as the stellar aggregates showing the Na–O anticorrelation." No consensus, however, exists as to the cause of these anticorrelations. The principal explanations, mostly with an emphasis on two intracluster populations of roughly commensurate size, include (i) chemical enrichment of the later generation by the ejecta of AGB stars of an earlier one (e.g., D'Ercole et al. 2010, and references therein), (ii) enrichment of a later generation by the ejecta of earlier rotating massive stars (Decressin et al. 2007, and references therein), (iii) a scenario in which "low-mass pre-main-sequence stars accrete enriched material released from interacting massive binary and rapidly rotating stars on to their circumstellar discs" (Bastian et al. 2013), and (iv) supermassive black holes early in the cluster lifetime (Denissenkov & Hartwick 2014). In stark contrast, only 3% of the Galactic halo stellar population exhibits these anticorrelated abundance patterns (Martell et al. 2011).
What then do we know about the existence of these abundance anticorrelations in the dSph systems? To the best of our knowledge, the most comprehensive studies relevant to this are those of Shetrone et al. (2003), McWilliam et al. (2013), and Fabrizio et al. (2015). Shetrone et al. (2003) found only subsolar values of [Na/Fe] in Sculptor (5/5 stars), Fornax (4/5 stars), and Carina (5/5 stars), more like that of the Galactic halo than its globular clusters; for the Sagittarius dSph McWilliam et al. (2013) reported "no detectable signature of pollution by proton-burning products"; and Fabrizio et al. (2015) presented results for [O/Fe] in nine stars in Carina, all but one of which have [O/Fe] > +0.4 (albeit all of these having [Na/Fe] in the range of −0.1 to +0.7). We confirm their results.22 Figure 28 presents [Na/Fe] versus [O/Fe] for the stars in Carina for which we have spectra (Table 1), together with results for the Galaxy's globular clusters M3, M4, M5, and M13 from Kraft et al. (1992, 1997) and Ivans et al. (1999, 2001).23 In the figure, one sees that the Carina stars are confined to high [O/Fe] and low [Na/Fe], similar to what is expected from the results of Martell et al. (2011) for Galactic halo stars, while those in the clusters not only occupy that region but also stretch to low-[O/Fe], high-[Na/Fe] values, driven by the operation of nuclear (p, γ)-reactions (a solution first described by Denisenkov & Denisenkova [1990] to explain the Na–O anticorrelation), peculiar to the clusters.
Figure 28. [Na/Fe] vs. [O/Fe] for red giants in Carina (large red circles; present work) and in the globular clusters M3, M4, M5, and M13 (small green circles). We note that all estimates assume LTE. Arrows are used for Carina to indicate when only an upper limit is available for the [O/Fe] and/or [Na/Fe] values. See text for discussion of the difference between the two distributions.
Download figure:
Standard image High-resolution imageWhat drives this basic difference between the globular clusters and Carina? The obvious physical candidates are that the dSph is dark matter dominated, is of considerably lower central density (∼0.3 M⊙/pc3 [Walker et al. 2009b], compared with ∼10,000 M⊙/pc3 for a typical cluster [Pryor & Meylan 1993]), and had star formation episodes lasting considerably longer (say, 2−3 Gyr) than occurred in the globular clusters (<1 Gyr). There are obvious differences in formation histories—Carina has some 3.4 × 106 M⊙ of dark matter within its half-light radius (Walker et al. 2009b), while the clusters are currently dark matter free. Finally, Carina formed well away from other stellar systems, while the Galactic globular clusters initially evolved in an environment more challenging for the survival of their gaseous components. It will be interesting to see which, if any, of these comparisons lie at the bottom of the abundance pattern differences between the dSph and globular clusters.
12. The Extremely Lithium Enhanced Star CC11560
Among the stars in Table 1, for which we have high-resolution spectra, CC11560 exhibits an exceptionally strong Li λ6707 line. For all other stars in the table, this feature cannot be detected. Canonical stellar evolution models predict that lithium is readily destroyed as stars ascend the RGB (Iben 1967). There are, however, a small number of lithium-rich red giant stars in globular clusters (Wallerstein & Sneden 1982; Brown et al. 1989; Kraft et al. 1999) and dSph galaxies (Kirby et al. 2012). We refer the reader to Kirby et al. for a comprehensive discussion of the origin of this effect. Suffice it here to say that the most likely source of the excess Li is the so-called Cameron–Fowler mechanism (Cameron & Fowler 1971), which was proposed to occur during helium shell flashes and/or "cool bottom processing" in which it is produced in the hydrogen-burning shell (Sackmann & Boothroyd 1999). This Li is then destroyed during deep convective mixing as the star moves further up the giant branch.
We measured the lithium abundance in CC11560 via spectrum synthesis of the λ6707 resonance line, as well as from the λ6103 subordinate line (see Figure 29). We computed line profiles adopting log gf = 0.17 and 0.58 for the λλ6707 and 6103 lines (Lindgård and Nielson 1977), respectively, assuming LTE, and applied NLTE corrections following Lind et al. (2009), leading to an average abundance of A(Li)NLTE = +3.36. To our knowledge, CC11560 is the first Li-rich red giant found in the Carina dwarf galaxy.
Figure 29. Comparison between the observed spectrum of the lithium-enhanced CC11560 (crosses) and LTE model atmospheric synthetic spectra. The solid lines represent the adopted fit together with two lines that bracket the best fit by ±0.5 dex (top panel) and ±0.2 dex (bottom panel), while the dotted line in each panel is the case of zero lithium. The adopted lithium abundances, on the NLTE scale, are given in the lower right corner of the panels. The //[Fe/H] values for CC11560 are also presented.
Download figure:
Standard image High-resolution imageKirby et al. (2012) studied 15 Li-rich red giants in dSph galaxies covering a range in magnitudes brighter than the RGB bump and reported that they represent ∼1% of the RGB population in that region of the CMD. This is of the same order as the ratio of 1/32 for the RGB stars of which we have spectra. In their sample, the abundances ranged over +1.76 < A(Li)NLTE < +3.85. CC11560 lies within this range. Finally, Kirby et al. (2012) reported that there was no correlation between lithium enhancement and any other parameter and concluded that these stars are likely experiencing a brief and possibly universal phase of stellar evolution. In CC11560, also, no element other than Li is unusual with respect to the values found for other program stars. It thus appears that CC11560 belongs to the population of lithium-rich stars discussed by Kirby et al. (2012). We refer the reader to their work for a more detailed discussion of the phenomenon.
13. Summary
- 1.We have presented high-resolution, moderate-S/N observations of 32 RGB stars in the Carina dSph galaxy, which have been analyzed using 1D/LTE model atmosphere techniques to produce chemical abundances for ∼20 elements. The analysis has been extended to Carina red giants for which observational data of a similar quality are available in the literature. Abundances are available for a total sample of 63 independent stars within this system.
- 2.The total sample, which originates from four sources, is incomplete in two ways. There are relatively fewer fainter stars than in a complete sample and a small dearth of Carina members blueward of its well-defined RGB (evident from comparison with complete radial velocity samples, as pointed out in Paper I).
- 3.Bearing in mind the above caveats, the sample has , with dispersion σ[Fe/H] = 0.33 dex, and an [α/Fe] distribution with mean value and dispersion σ[α/Fe] = 0.13 dex.
- 4.Consideration of the available α-elements shows little evidence for significant differences in abundances of the individual α-elements relative to that of iron. For example, and differ by less than 0.1 dex. The mean value of [α/Fe] (the average of Mg, Ca, and Ti) for Carina is smaller by ∼0.25 dex than that of the Galactic halo.
- 5.Calcium, which has the most accurately determined abundance of the α-elements, shows an asymmetric distribution in [Ca/Fe] toward smaller values at all [Fe/H], most significantly in the range −2.0 < [Fe/H] < −1.0, where the density of points is highest—suggestive of incomplete mixing of the ejecta of SNe Ia and the ambient medium of each of Carina's generations.
- 6.Comparison of the abundance distributions of the individual stars with the abundance predictions of SN Ia models of Iwamoto et al. (1999), together with the formalism of Venn et al. (2012), shows evidence for large Type Ia enrichment within the material that formed some 10% of the stars in our sample, confirming the results of Venn et al. (2012).
- 7.Very approximate ages, internally accurate to only 3–4 Gyr, have been determined by comparing the positions of the stars in the CMD with the isochrones of Demarque et al. (2004), VandenBerg et al. (2006), and Dotter et al. (2008). A comparison of the results suggests that the external errors from the use of different isochrones are also considerable.
- 8.That said, the AMRs from the present work and from the CMD analysis presented in Paper I are in general agreement, with both presenting a monotonic progression from (Age, [Fe/H]) ∼ (13 Gyr. −2.0) to ∼ (1−2 Gyr, −1.0). There is, however, an observed excess of stars below [Fe/H] in the high-resolution spectroscopic data. (See also Paper I, Section 5.) It will be important to understand whether this is due to a selection effect favoring metal-poor stars, to spectroscopic measurement error, or perhaps to the existence of stars with [Fe/H] ∼ −2.0 that were formed before the first population identified in the synthetic CMD analysis, which has . We conjecture in the present work that our "first" (and oldest) population in Paper I is multimodal, and that we essentially identified only a major subcomponent of the oldest population, while there exists a more metal-poor, presumably older and minor subcomponent as well, perhaps resulting from simple inhomogeneous mixing of the early star-forming gas and/or active accretion of lower-mass systems in the earliest stages of Carina's formation.
- 9.We demonstrate that the Na–O anticorrelation found in all of the Galactic globular clusters is not present in Carina, confirming the results of Shetrone et al. (2003), who first demonstrated that the abundance of Na is subsolar in Carina (and in three other dSph systems), McWilliam et al. (2013), and Fabrizio et al. (2015).
- 10.We report the serendipitous discovery of an extremely lithium-enhanced red giant, CC11560, which has A(Li)NLTE = +3.36, a characteristic exhibited by only ∼1% of the red giants in the Galactic globular clusters and its dSph satellites.
We are extremely grateful to P. B. Stetson, M. J. Irwin, and M. Gullieuszik for their generosity in providing photometry for the objects investigated in the present work. Studies at RSAA, ANU, of the Galaxy's most metal-poor stars and its dwarf galaxy satellite systems by J.E.N. and D.Y. are supported by Australian Research Council grants DP0663562, DP0984924, DP120100475, DP150100862, and FT140100554. K.A.V. acknowledges support from the Canadian NSERC Discovery Grants program. This work was partly supported by the European Union FP7 program through ERC grant no. 320360.
Facility: VLT:Kueyen(UVES).
Appendix: Cross-identification and Averaged Abundances for the 63 Independent Carina Red Giants
Table 14 presents cross-identifications and coordinates of the 63 independent stars analyzed in the present work. The names in columns (1)–(4) are those used here and in the works of Venn et al. (2012), Shetrone et al. (2003), and Lemasle et al. (2012), respectively.
Table 14. Cross-identification and Coordinates of Program Stars
| This Worka | Venn et al.a | Shetrone et al.a | Lemasle et al.a | R.A. (2000) Decl. |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| MKV0842 | 06 40 22.51 −50 59 01.9 | |||
| CC10194 | 06 40 30.82 −50 59 15.0 | |||
| MKV0677 | 06 40 31.12 −50 55 24.5 | |||
| MKV0628 | 06 40 35.37 −50 54 07.6 | |||
| MKV0640 | 06 40 40.82 −50 54 29.2 | |||
| MKV0914 | 06 40 42.49 −51 00 42.7 | |||
| MKV0925 | 06 40 43.17 −51 01 06.6 | |||
| Car-7002 | 06 40 49.15 −51 00 32.9 | |||
| MKV0812 | 06 40 51.62 −50 58 21.7 | |||
| CC09869 | MKV0825 | 06 40 56.95 −50 58 38.2 | ||
| MKV0780 | 06 40 57.09 −50 57 44.3 | |||
| MKV0976 | 06 40 57.68 −51 02 40.7 | |||
| CC11388 | 06 40 58.04 −51 02 00.0 | |||
| CC07452 | Car-612 | 06 40 58.47 −50 53 35.2 | ||
| CC11560 | MKV1009 | 06 40 59.29 −51 02 26.4 | ||
| CC12038 | MKV1012 | 06 41 00.31 −51 03 42.9 | ||
| CC11217 | 06 41 05.01 −51 01 35.8 | |||
| MKV0596 | 06 41 05.35 −51 05 25.5 | |||
| CC08447 | 06 41 10.54 −50 55 52.8 | |||
| CC09226 | MKV0770 | 06 41 12.29 −50 57 25.8 | ||
| Car-524 | 06 41 14.68 −50 51 09.7 | |||
| Car-1087 | 06 41 15.45 −51 01 16.0 | |||
| MKV0880 | 06 41 15.66 −50 59 47.9 | |||
| CC10690 | MKV0902 | 06 41 16.30 −51 00 18.5 | ||
| CC10944 | 06 41 16.75 −51 00 53.8 | |||
| CC09179 | 06 41 17.92 −50 57 20.3 | |||
| CC09225 | Car-769 | 06 41 19.69 −50 57 25.4 | ||
| CC12039 | Car-1013 | 06 41 21.97 −51 03 43.1 | ||
| MKV0698 | 06 41 26.09 −50 55 43.7 | |||
| CC10686 | MKV0900 | 06 41 27.18 −51 00 18.2 | ||
| CC10802 | 06 41 27.53 −51 00 34.7 | |||
| MKV0740 | 06 41 29.08 −50 56 46.5 | |||
| MKV1061 | 06 41 29.15 −51 05 22.3 | |||
| CC08695 | M12 | 06 41 36.47 −50 56 23.2 | ||
| MKV0948 | 06 41 37.65 −51 01 43.7 | |||
| CC06122 | Car-484 | 06 41 39.62 −50 49 58.8 | ||
| CC07889 | MKV0652 | 06 41 40.83 −50 54 45.7 | ||
| MKV1007 | 06 41 44.63 −51 03 31.1 | |||
| MKV0577 | 06 41 45.03 −50 52 49.0 | |||
| MKV0743 | 06 41 45.91 −50 56 54.3 | |||
| CC06486 | MKV0514 | 06 41 45.99 −50 51 00.6 | ||
| M10 | 06 41 46.34 −51 01 22.5 | |||
| CC10414 | 06 41 47.62 −50 59 44.0 | |||
| M4 | 06 41 48.20 −50 55 01.4 | |||
| CC08615 | 06 41 49.58 −50 56 11.3 | |||
| CC08788 | 06 41 50.09 −50 56 35.0 | |||
| CC09633 | Car-5070 | 06 41 53.83 −50 58 10.9 | ||
| CC09507 | 06 41 54.07 −50 57 56.6 | |||
| CC09000 | M3 | 06 41 54.58 −50 57 00.6 | ||
| CC09929 | 06 41 54.83 −50 58 46.8 | |||
| CC10318 | M2 | 06 41 57.62 −50 59 32.5 | ||
| MKV0458 | 06 41 58.19 −50 48 58.0 | |||
| MKV0397 | 06 41 58.27 −50 46 41.4 | |||
| CC10038 | MKV0840 | 06 42 02.79 −50 58 59.2 | ||
| CC09430 | 06 42 05.37 −50 57 48.2 | |||
| MKV0916 | 06 42 08.97 −51 00 48.0 | |||
| CC06975 | 06 42 10.84 −50 52 20.4 | |||
| CC08469 | Car-705 | 06 42 17.39 −50 55 55.0 | ||
| MKV0729 | 06 42 17.45 −50 56 26.3 | |||
| MKV0556 | 06 42 22.26 −50 52 09.5 | |||
| MKV0733 | 06 42 30.38 −50 56 33.3 | |||
| MKV0614 | 06 42 37.95 −50 53 37.6 | |||
| MKV0708 | 06 42 38.52 −50 56 00.8 |
Note.
aThe headers in columns (1)−(4) refer to the present work, Venn et al. (2012), Shetrone et al. (2003), and Lemasle et al. (2012), respectively.A machine-readable version of the table is available.
Download table as: DataTypeset image
Finally, Table 15 presents the average relative abundances, together with their errors, for these 63 stars in Tables 8, 10, and 11, which were introduced in Section 6. In cases where a star appears in more than one table, the abundances were averaged with weighting by the inverse squares of their errors in the relevant tables. In Table 15 there are 63 two-line blocks, in which the first and second lines contain the average abundances and their errors, respectively. Stellar identifications are given in the first column, and in cases where multiple observations are involved, the two star names are given in the first column of the two lines of the block.
Table 15. Average [Fe/H], [X/Fe], and Errorsa for the 63 Independent Carina Red Giants
| Objectb | [Fe/H] | O | Na | Mg | Si | Ca | Sc | Ti | V | Cr | Mn | Fe ii | Co | Ni | Cu | Ba | La | Nd | Eu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MKV0842 | −1.39 | ⋯ | ⋯ | 0.30 | ⋯ | 0.50 | ⋯ | 0.26 | ⋯ | −0.29 | ⋯ | 0.50 | ⋯ | ⋯ | ⋯ | −0.66 | ⋯ | ⋯ | ⋯ |
| 0.15 | ⋯ | ⋯ | 0.21 | ⋯ | 0.20 | ⋯ | 0.16 | ⋯ | 0.21 | ⋯ | 0.19 | ⋯ | ⋯ | ⋯ | 0.22 | ⋯ | ⋯ | ⋯ | |
| CC10194 | −1.42 | 0.17 | −0.31 | 0.15 | 0.18 | 0.01 | −0.27 | 0.22 | −0.25 | 0.00 | −0.90 | −0.01 | ⋯ | −0.25 | ⋯ | 0.13 | 0.24 | −0.31 | ⋯ |
| 0.15 | 0.27 | 0.24 | 0.14 | 0.27 | 0.08 | 0.15 | 0.12 | 0.19 | 0.23 | 0.17 | 0.21 | ⋯ | 0.12 | ⋯ | 0.22 | 0.26 | 0.25 | ⋯ |
Notes.
aFor each object the two rows contain [Fe/H] and [X/Fe] and σTot, respectively. bIn each block, one or two names are given when one or two observations are available.Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Footnotes
- *
Based on observations collected at the European Southern Observatory, Paranal, Chile (Proposal 180.B-0806(B); PI: G. Gilmore).
- 4
The parameters of the youngest population are less certain than those of the other three, and given that it is less centrally concentrated, it may not be directly related to them. We conjectured that rather than having [Fe/H] ∼ −1.15, it might be more metal-poor by Δ[Fe/H] ∼ 0.3 dex. We also noted that more work is needed to determine whether Carina's horizontal branch, its blue stragglers, and its stellar rotation might play a role in determining the position of this population in the CMD.
- 5
- 6
We note here for completeness that a comparison of the final sample of 63 spectroscopic red giants presented in this paper with the radial-velocity-selected samples of Koch et al. (2006) and Walker et al. (2009a) shows that our sample is incomplete insofar as it is narrower in the (MV, ) CMD than theirs, by some 3σ–4σ. See Paper I for further discussion of this point.
- 7
- 8
- 9
A referee has suggested that double-binning of the data will affect the measurement of EWs. This is not the case. In the FLAMES manual http://www.eso.org/sci/facilities/paranal/instruments/flames/doc/VLT-MAN-ESO-13700-2994_p99.pdf Section 2.1 notes that there are five pixels per FLAMES fiber. Double-binning means that there are 2.5 pixels per resolution element, which is not undersampled according to Nyquist sampling, and thus the resolution remains at R = 47,000. We also note that the spectral lines we measured have a median FWHM of ∼0.28 Å, which corresponds to some 10 double-binned pixels.
- 10
- 11
The sample comprises the stars in our Table 1, excluding CC06975.
- 12
- 13
- 14
We do not plot results for Al since this element was detected in only one star for which we have spectra.
- 15
The reader may ask what causes there to be a few stars having values above 0.0 in the right panel of Figure 22 but none below 0.0 in the left. This results from the definitions: put most simply, admits positive values, while Fraction does not permit negative ones.
- 16
- 17
- 18
- 19
- 20
We note that while we have chosen to use the Dartmouth ages in the presentation, the same essential behavior is seen when we use the Victoria–Regina and Yale–Yonsei isochrones.
- 21
A referee made the following related comment on the large spread in [Fe/H] in our Figure 26. "Data plotted in the left panel indicate that the old stellar subpopulation experienced, at fixed age, a metal enrichment of the order of one dex. Is this metal enrichment supported by the spread in magnitude of the subgiant branch of the old population?" In Carina's (MV, ) CMD, the SGB of this "first" population has a magnitude spread at a given color of ΔMV ∼ 0.40 mag. We first compare this with the isochrones of Dotter et al. (2008) for two models having Δ[Fe/H] = 0.8 and age difference ΔAge = 0.0 —[Fe/H]/[[α/Fe]/Age = −2.4/+0.2/13.0 and −1.6/+0.2/13.0. In the region of the observed SGB these isochrones are parallel curves separated by ΔMV ∼ 0.40 mag that fit within the observations. More to the conjecture that we make here, if one admits an age difference ΔAge = −2.0 Gyr (i.e., the more metal-poor stars are older) and consider isochrones [Fe/H]/[α/Fe]/Age = −2.4/+0.2/14.0 and −1.6/+0.2/12.0, the corresponding sequences, while falling well within the region of the observed SGB, are closer together, with ΔMV ∼ 0.1−0.3 mag (diverging with increasing color).
- 22
We are unable to comment on the existence or otherwise of an Al–O anticorrelation in Carina as is found in globular clusters, since Al was detected in only one star for which we have spectra.
- 23
These clusters have [Fe/H] in the range of −1.5 to −1.2, within which all but one of the Carina stars in Figure 28 having both Na and O abundances lie (allowing for an error of measurement 0.15 dex for the [Fe/H] values).
















































![${\sigma }_{[\mathrm{Fe}/{\rm{H}}]}$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn40.gif)














![${\sigma }_{[{\rm{M}}/{\rm{H}}]}$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn55.gif)










![${\sigma }_{[{\rm{M}}/{\rm{H}}]}$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn66.gif)

![${\sigma }_{[{\rm{X}}/\mathrm{Fe}]}$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn68.gif)






![${\sigma }_{[{\rm{M}}/{\rm{H}}]}=0.15$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn75.gif)





![$\langle {\rm{\Delta }}[\mathrm{Fe}/{\rm{H}}]\rangle =-0.01\pm 0.08,$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn80.gif)


![$\langle {\rm{\Delta }}[\mathrm{Fe}/{\rm{H}}]\rangle \,=0.01\pm 0.05$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn83.gif)
![$\langle [\mathrm{Fe}/{\rm{H}}]\rangle =0.33\,\pm 0.04$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn84.gif)



![$\langle {\rm{\Delta }}[{\rm{O}}/\mathrm{Fe}]\rangle =0.23\,\pm 0.04$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn87.gif)
![$\langle {\rm{\Delta }}[\mathrm{Na}/\mathrm{Fe}]\rangle =0.49\pm 0.07$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn88.gif)
![$\langle {\rm{\Delta }}[\mathrm{Mg}/\mathrm{Fe}]\rangle =0.19\pm 0.05$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn89.gif)
![$\langle {\rm{\Delta }}[\mathrm{Ca}/\mathrm{Fe}]\rangle =0.22\pm 0.03$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn90.gif)
![$\langle {\rm{\Delta }}[{\rm{O}}/{\rm{H}}]\rangle =-0.09\pm 0.05$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn91.gif)
![$\langle {\rm{\Delta }}[\mathrm{Na}/{\rm{H}}]\rangle =0.15\pm 0.06$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn92.gif)
![$\langle {\rm{\Delta }}[\mathrm{Mg}/{\rm{H}}]\rangle =-0.13\pm 0.03$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn93.gif)
![$\langle {\rm{\Delta }}[\mathrm{Ca}/{\rm{H}}]\rangle =-0.10\,\pm 0.04$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn94.gif)
![$\langle {\rm{\Delta }}[{\rm{X}}/{\rm{H}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn95.gif)
![$\langle {\rm{\Delta }}[{\rm{X}}/\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn96.gif)



















![$\langle [{\rm{O}}\,{\rm{I}}/\mathrm{Fe}]\rangle =0.46\pm 0.04$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn107.gif)
![$\langle [\mathrm{Na}\,{\rm{I}}/\mathrm{Fe}]\rangle =-0.28\pm 0.04$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn108.gif)
![$\langle [\mathrm{Mg}/\mathrm{Fe}]\rangle =0.12\pm 0.02$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn109.gif)
![$\langle [\mathrm{Si}/\mathrm{Fe}]\rangle =0.28\,\pm 0.04,\langle [\mathrm{Ca}/\mathrm{Fe}]\rangle =0.04\pm 0.01$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn110.gif)
![$\langle [\mathrm{Ti}/\mathrm{Fe}]\rangle =0.18\pm 0.01$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn111.gif)

![$\langle [\mathrm{Sc}/\mathrm{Fe}]\rangle =0.00\pm 0.02$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn113.gif)
![$\langle [{\rm{V}}/\mathrm{Fe}]\rangle =-0.05\pm 0.03$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn114.gif)
![$\langle [\mathrm{Mn}/\mathrm{Fe}]\rangle =-0.37\pm 0.01$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn115.gif)
![$\langle [\mathrm{Mn}\,{\rm{i}}/\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn116.gif)
![$\langle [\mathrm{Cr}/\mathrm{Fe}]\rangle =-0.07\pm 0.02$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn117.gif)
![$\langle [\mathrm{Ni}/\mathrm{Fe}]\rangle =-0.10\pm 0.01$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn118.gif)

![$\langle [\mathrm{Fe}\,{\rm{ii}}/\mathrm{Fe}]\rangle =0.25\pm 0.02$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn120.gif)







![$\langle [\mathrm{Mg}/\mathrm{Ca}]\rangle =0.12\pm 0.03$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn128.gif)

![$\langle [\alpha /\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn129.gif)




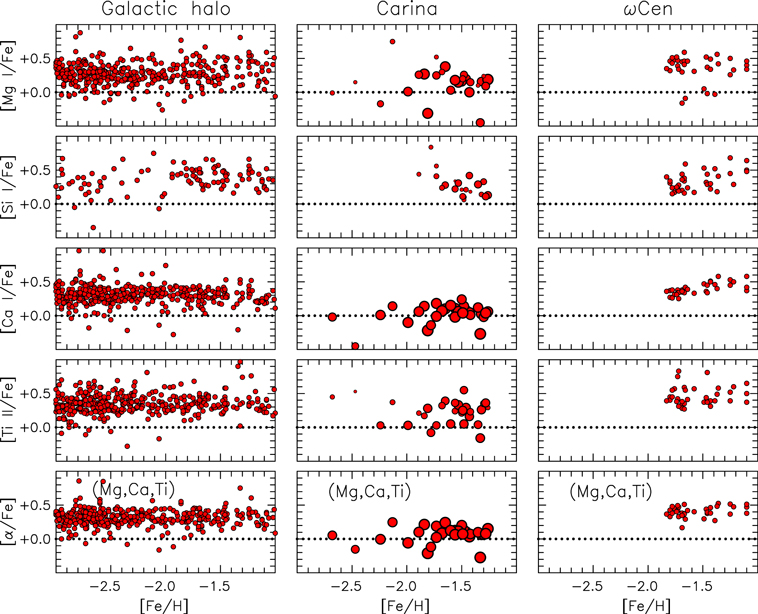

![$\langle [\alpha /\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn134.gif)
![$\langle [\alpha /\mathrm{Fe}]\rangle =0.04\pm 0.08$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn135.gif)



![$\langle [\mathrm{Mg}/\mathrm{Ca}]\rangle =0.13\pm 0.03$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn139.gif)
![$\langle [\mathrm{Mg}/\mathrm{Ca}]\rangle \,=\,-0.025\pm 0.008$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn140.gif)













![$\langle {\rm{\Delta }}[{{\rm{X}}}_{{\rm{i}}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn151.gif)
![$\langle {\rm{\Delta }}[{{\rm{X}}}_{{\rm{i}}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn152.gif)

![$\langle {\rm{\Delta }}[{{\rm{X}}}_{i/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn154.gif)

![$\langle {\rm{\Delta }}[{{\rm{X}}}_{{\rm{i}}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn156.gif)


![$\langle {\rm{\Delta }}[{{\rm{X}}}_{{\rm{i}}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn160.gif)

![$-\langle {\rm{\Delta }}[{{\rm{X}}}_{{\rm{i}}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn162.gif)





















![$\langle [\mathrm{Fe}/{\rm{H}}]\rangle =-1.59$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn179.gif)
![$\langle [\alpha /\mathrm{Fe}]\rangle =0.07$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn180.gif)
![$\langle [\mathrm{Mg}/\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn181.gif)
![$\langle [\mathrm{Ca}/\mathrm{Fe}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn182.gif)

![$\langle [\mathrm{Fe}/{\rm{H}}]\rangle =-1.85\pm 0.05$](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn184.gif)

![$\langle {\rm{\Delta }}[{{\rm{X}}}_{{i}/\mathrm{Fe}}]\rangle $](https://content.cld.iop.org/journals/0067-0049/230/2/28/revision1/apjsaa755eieqn157.gif)


