Abstract
This paper presents a single mode model that accurately predicts the coupling of applied nonaxisymmetric fields to the plasma response that induces neoclassical toroidal viscosity (NTV) torque in DIII-D H-mode plasmas. The torque is measured and modeled to have a sinusoidal dependence on the relative phase of multiple nonaxisymmetric field sources, including a minimum in which large amounts of nonaxisymmetric drive is decoupled from the NTV torque. This corresponds to the coupling and decoupling of the applied field to a NTV-driving mode spectrum. Modeling using the perturbed equilibrium nonambipolar transport (PENT) code confirms an effective single mode coupling between the applied field and the resultant torque, despite its inherent nonlinearity. The coupling to the NTV mode is shown to have a similar dependence on the relative phasing as that of the IPEC dominant mode, providing a physical basis for the efficacy of this linear metric in predicting error field correction optima in NTV dominated regimes.
Export citation and abstract BibTeX RIS
1. Introduction and motivation
Externally applied nonaxisymmetric magnetic fields could provide an important rotation control tool in future large devices which are expected to have low momentum input from neutral beam injection. Applied magnetic nonaxisymmetric fields (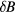 ) in tokamaks smaller than the axisymmetric field (B) by many orders of magnitude (
) in tokamaks smaller than the axisymmetric field (B) by many orders of magnitude (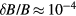 ) can generate significant neoclassical toroidal viscosity (NTV), leading to toroidal rotation damping [1–3] or drive [4–6]. Since rotation strongly influences stability and confinement of the plasma, an understanding of the coupling between the applied nonaxisymmetric fields and the resultant torque can provide an important tool for the optimization of tokamak performance.
) can generate significant neoclassical toroidal viscosity (NTV), leading to toroidal rotation damping [1–3] or drive [4–6]. Since rotation strongly influences stability and confinement of the plasma, an understanding of the coupling between the applied nonaxisymmetric fields and the resultant torque can provide an important tool for the optimization of tokamak performance.
Predictive control of the NTV torque, however, is complicated. This is in part due to the detailed velocity space structure of the torque that is dependent on different particle orbits, precessions, and collisions. A number of theoretical NTV approximations and corresponding computational models have been developed to explain and guide experiments, each with a unique physics emphasis. These include large aspect ratio models with detailed collision operators [7, 8], collisionality regime models [9, 10], Krook collisionality models emphasizing bounce harmonic resonances and general geometry [11, 12], and stability models that utilize the kinetic energy equivalency principle [13–15]. Extensive efforts have benchmarked these models and the detailed kinetic physics captured therein [8, 14, 15], providing confidence in the models and a clear understanding of their limits of applicability.
The control of NTV torque is further complicated by nonlinear poloidal mode coupling, inherent in every model. The NTV torque from one nonaxisymmetric field source cannot be summed together with the NTV torque from a second nonaxisymmetric field source to find the torque caused by the two sources together. This increases the computational burden for predictions of how applied fields will combine with intrinsic error fields, for example. The nonlinearity makes it necessary to explicitly model every combination of interest. Compounding this, the 'nonresonant' nature of NTV means that perturbations throughout the plasma contribute to the torque. Without a-priori knowledge of which components are significant for the torque, the nullification of NTV from intrinsic nonaxisymmetries would require a perfect matching of the source spectrum in order to remove the perturbation everywhere in the plasma. This would be impractical, and the infinite possibilities of source spectra would render finite error field correction (EFC) coil arrays inefficient for NTV control. The application of desired torque using applied fields would contain similar difficulties, as every combination of fields and plasma equilibria would need to be modeled independently in order to gain predictive control capabilities.
Many of the difficulties in predicting the torque from external fields are alleviated, however, if the torque can be described by a single mode model. In a single mode model the extent to which an external field is coupled to a defined spectrum fully describes the response physics of interest. This enables linear summation of the coupling of multiple nonaxisymmetric source's and allows, among other things, any one source to perfectly null the effect of any other source. For this to happen, there must be a single plasma response structure that either fully encapsulates the physics of interest (the pitch-resonant response at a rational surface for tearing studies for example) or is expected to dominate due to its lower stability (a marginally stable resistive wall mode for example). One single mode model in particular, the IPEC 'dominant mode' has been used extensively in EFC predictions for current and future high pressure tokamaks [16–20]. This model makes use of linearized ideal MHD to calculate the coupling between applied Fourier harmonics and the pitch-resonant flux at each rational surface in the plasma. A singular value decomposition (SVD) analysis of this matrix provides an eigenbasis for external field coupling to the root mean square resonant field [16, 21, 22].
This work shows the NTV torque is closely coupled to the dominant mode of the plasma response and provides a physics basis for the reduction of the NTV spectral dependence to a single parameter quantifying the extent to which an external field overlaps with the dominant mode (first left-singular vector of the SVD). The analysis uses the PENT [12] model to calculate the full bounce-harmonic, cross-regime, general geometry torque so as not to sacrifice generality in the rich kinetic physics of NTV. The result, an effective single mode coupling despite the general NTV model, provides a powerful new tool that can be used for predictive control of the NTV rotation damping or drive using non-axisymmetric field coils. In addition to simplifying the NTV spectral dependence greatly, these results establish the physical importance of the non-resonant components of the dominant mode.
This paper is organized as follows. An experiment designed to test the coupling of varied nonaxisymmetric spectra to NTV torque is described in section 2. The PENT predicted coupling of NTV torque to a single mode and relation to the linear IPEC dominant mode overlap metric are presented in section 3. The implications of this reduction to a single mode model are then discussed in section 4.
2. Experimental method
2.1. Configuration
The coupling of the NTV torque to an applied nonaxisymmetric spectra was measured in a quiescent high confinement scenario (QH-mode) in the DIII-D tokamak. The QH-mode is characterized by the high confinement of H-mode, an absence of edge localized modes (ELMs), and the presence of an edge harmonic oscillation (EHO) [23, 24]. The QH-mode is dependent on rotation shear in the edge but independent of its sign, allowing for either co-current or counter-current rotation [6, 25, 26]. Counter-current rotation was chosen for this work, taking advantage of the observation that nonaxisymmetric fields drive QH-mode plasmas in DIII-D toward a counter-current neoclassical offset rotation [6, 26]. This distinguishes the NTV momentum source from competing terms in the momentum balance such as resonant braking, which is a momentum sink independent of the sign of the rotation. Note that fast ion losses can produce some counter-current torque from the thermal ion return current. This is offset by loss of injected counter-current torque however, typically leading to a reduced effect of prompt ion losses on the angular momentum during counter NBI [27].
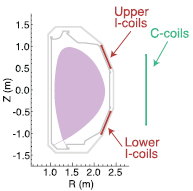
Perturbative nonaxisymmetric fields were applied to these plasmas using the three nonaxisymmetric coil arrays of six discrete coils each shown in figure 1. For the purposes of this work, the C-coil array external to the vessel was used for correction of the intrinsic  error field. The upper I-coil (IU) and lower I-coil (IL) arrays internal to the vessel were used to apply the maximum additional n = 2 perturbation, corresponding to a peak current amplitude of 4.3 kA. The poloidal spectrum of the applied nonaxisymmetric field was varied by changing the relative toroidal phase of currents in the two I-coil arrays between discharges.
error field. The upper I-coil (IU) and lower I-coil (IL) arrays internal to the vessel were used to apply the maximum additional n = 2 perturbation, corresponding to a peak current amplitude of 4.3 kA. The poloidal spectrum of the applied nonaxisymmetric field was varied by changing the relative toroidal phase of currents in the two I-coil arrays between discharges.
Figure 1. This schematic of the poloidal cross-section of the DIII-D vessel includes the positions of the in-vessel (I) and external correction (C) coil arrays. The lower single null QH-mode plasma shape used in these experiments is shown in purple.
Download figure:
Standard image High-resolution imageFigure 2 shows the variation in n = 2 poloidal spectra applied to the plasma surface obtained by adjusting the phasing between the IL and IU arrays. Consistent with the experiment, these spectra were obtained with the IU phase  held constant. Changes in the IL phase
held constant. Changes in the IL phase 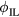 thus produce changes in the upper–lower phasing,
thus produce changes in the upper–lower phasing, 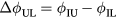 . There is a sharp peak at m = −1 to 1 in all cases. The secondary peak in the positive m spectra (right-handed pitch, like the field lines) shifts from m = 8 to 16. Also shown, is the IPEC calculated 'dominant mode' spectrum, which is discussed in detail in section 3.2 and peaks at m = 15 in the QH-mode equilibrium.
. There is a sharp peak at m = −1 to 1 in all cases. The secondary peak in the positive m spectra (right-handed pitch, like the field lines) shifts from m = 8 to 16. Also shown, is the IPEC calculated 'dominant mode' spectrum, which is discussed in detail in section 3.2 and peaks at m = 15 in the QH-mode equilibrium.
Figure 2. The IPEC dominant mode (black) and applied poloidal spectra in PEST coordinates on the IPEC control surface for various n = 2 I-coil phasings. Both upper and lower I-coils have 4.3 kA n = 2 current waveforms, and the scanned phasings are indicated in the legend.
Download figure:
Standard image High-resolution image2.2. NTV measurement technique
In establishing the initial equilibrium, neutral beam injected (NBI) torque was used to produce strong rotation in the counter-current direction of the ion neoclassical offset. The amount of NBI was then reduced such that the angular momentum  evolved on a time scale that was slow compared to the momentum confinement time
evolved on a time scale that was slow compared to the momentum confinement time  and the plasma remained in torque balance. The integral angular momentum measured in the reference plasma with no applied I-coil field follows a simplified angular momentum evolution,
and the plasma remained in torque balance. The integral angular momentum measured in the reference plasma with no applied I-coil field follows a simplified angular momentum evolution,
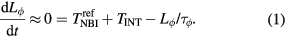
The injected torque 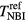 balances the intrinsic
balances the intrinsic 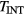 [28–30] and viscous torque approximated by
[28–30] and viscous torque approximated by 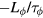 . In the presence of nonaxisymmetric fields, additional terms corresponding to the NTV torque
. In the presence of nonaxisymmetric fields, additional terms corresponding to the NTV torque 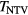 , additional prompt ion loss, and resonant braking may appear in the right hand side of equation (1). The resonant braking is damped with rotation [31–35], and initial studies with codes such as SPIRAL [36] show prompt ion loss torques in DIII-D on the order of 10% the injected torque. Assuming that the NTV was thus the dominant effect of the nonaxisymmetry in rotating plasmas during the controlled NBI ramp-down, the evolution of each discharge in the presence of applied nonaxisymmetric fields is described by,
, additional prompt ion loss, and resonant braking may appear in the right hand side of equation (1). The resonant braking is damped with rotation [31–35], and initial studies with codes such as SPIRAL [36] show prompt ion loss torques in DIII-D on the order of 10% the injected torque. Assuming that the NTV was thus the dominant effect of the nonaxisymmetry in rotating plasmas during the controlled NBI ramp-down, the evolution of each discharge in the presence of applied nonaxisymmetric fields is described by,

Combining this with (1) gives,
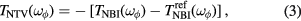
Under the assumptions that the momentum confinement time, moment of inertia, and intrinsic torque are unchanged by the small nonaxisymmetry.
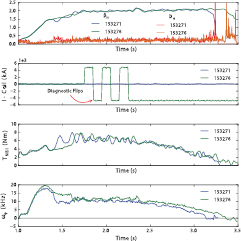
Equation (3) describes the NTV torque as the difference in NBI torque needed to obtain a given angular rotation with and without nonaxisymmetric fields. This was determined experimentally by comparing successive discharges with applied I-coil fields to a reference scenario with no applied I-coil fields. A comparison of two such discharges is given in figure 3. Large amounts (∼8 Nm) of NBI torque are used to produce fast rotation and  of approximately 2. At 2250 ms the NBI torque is slowly ramped toward zero, the rotation evolves in torque balance until reaching a bifurcation, characterized by a sudden locking to the tokamak frame, a disruption, and the termination of the discharge. The presence of nonaxisymmetric fields, indicated here as the amplitude of currents in the lower I-coil array, introduces a NTV torque that accelerates the plasma and extends the discharge. Note for the analysis presented in this paper the rotation is obtained from the velocity of the minority impurity C6+ measured by charge exchange recombination (CER) spectroscopy [37] and assumed to be proportional to that of the majority plasma ion species D+ .
of approximately 2. At 2250 ms the NBI torque is slowly ramped toward zero, the rotation evolves in torque balance until reaching a bifurcation, characterized by a sudden locking to the tokamak frame, a disruption, and the termination of the discharge. The presence of nonaxisymmetric fields, indicated here as the amplitude of currents in the lower I-coil array, introduces a NTV torque that accelerates the plasma and extends the discharge. Note for the analysis presented in this paper the rotation is obtained from the velocity of the minority impurity C6+ measured by charge exchange recombination (CER) spectroscopy [37] and assumed to be proportional to that of the majority plasma ion species D+ .
Figure 3. Evolution of a baseline QH-mode shot (153271) with no applied I-coil field and a phase scan shot (153276) with 4.3 kA n = 2 I-coils oriented such that 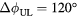 . In each case the
. In each case the 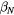 (top, green-blue) approaches two. The H-mode is ELM free, as evidenced by a lack of spikes in the diverter recycling light (top, red-orange). The I-coil currents (second from top) are turned on, flipped in sign (
(top, green-blue) approaches two. The H-mode is ELM free, as evidenced by a lack of spikes in the diverter recycling light (top, red-orange). The I-coil currents (second from top) are turned on, flipped in sign (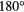 ) five times for diagnostic purposes, and then held constant from 2250 ms as the neutral beam torque (second from bottom) is ramped toward zero. Shots with applied I-coil fields maintain faster rotation (bottom) as the injected torque is removed.
) five times for diagnostic purposes, and then held constant from 2250 ms as the neutral beam torque (second from bottom) is ramped toward zero. Shots with applied I-coil fields maintain faster rotation (bottom) as the injected torque is removed.
Download figure:
Standard image High-resolution imageNote that equations (1) and (2) describe of the evolution of the integral angular momentum when integral torques are used. In general the torque, as expressed in equation (3), may vary radially with the rotation profile and temporally with the profile evolution. Figure 4, however, shows the angular momentum 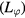 evolution has a strong radial dependence that can be used to reduce the number of free parameters. In the shot with applied fields the NTV props up edge
evolution has a strong radial dependence that can be used to reduce the number of free parameters. In the shot with applied fields the NTV props up edge 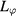 compared to the reference discharge, while the core angular momentum decreases steadily with decreasing NBI torque similar to the reference. This is consistent with the expectation that the n = 2 torque profile is concentrated in the plasma edge in DIII-D and modeling presented in section 3. This concentration of the torque profile suggests that the volume integrated NTV torque will be coupled to the modes of plasma response that dominate the perturbation in this specific region. It also enables the reduction of the NTV rotation dependence in equation (3) to a single variable: edge rotation. The edge rotation is defined here as
compared to the reference discharge, while the core angular momentum decreases steadily with decreasing NBI torque similar to the reference. This is consistent with the expectation that the n = 2 torque profile is concentrated in the plasma edge in DIII-D and modeling presented in section 3. This concentration of the torque profile suggests that the volume integrated NTV torque will be coupled to the modes of plasma response that dominate the perturbation in this specific region. It also enables the reduction of the NTV rotation dependence in equation (3) to a single variable: edge rotation. The edge rotation is defined here as 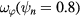 , although the ultimate result is insensitive to the exact location in the outer plasma as long as it is well inside the pedestal for all the discharges. In the remainder of this paper, this rotation is used as the dependent variable in which to compare the NBI torque trajectories between multiple discharges with different applied spectra and a reference with no applied fields and calculate the integral NTV torque according to equation (3).
, although the ultimate result is insensitive to the exact location in the outer plasma as long as it is well inside the pedestal for all the discharges. In the remainder of this paper, this rotation is used as the dependent variable in which to compare the NBI torque trajectories between multiple discharges with different applied spectra and a reference with no applied fields and calculate the integral NTV torque according to equation (3).
Figure 4. The angular momentum density temporal evolution of reference shot 153271 (blue) and shot 153276 with applied I-coil fields (green) at a surface in the deep core (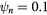 , dash-dot) and an outer surface (
, dash-dot) and an outer surface ( , solid). All curves are normalized to unity at 2300 ms.
, solid). All curves are normalized to unity at 2300 ms.
Download figure:
Standard image High-resolution image2.3. Observed NTV spectral dependance
The difference between the injected neutral beam torque required for equilibrium at a given rotation with and without applied nonaxisymmetric fields gives a direct measurement of the integral NTV torque according to equation (3). Thus, the NBI torque is mapped to a rotation variable as shown in figure 5. The NBI torques with and without applied fields as a function of the CER edge rotation are represented as third degree polynomial fits to points corresponding to the reconstructed profile times shown in figure 4, and the shaded error bars indicate propagation of errors determined by the fit accuracy. The temporal evolution of individual points is indicated in the reference shot, giving a sense of the scatter associated with the measurements. The two lines with 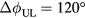 represent repeat discharges, showing the shot-to-shot reproducibility of the results. The vertical separation between the colored curves and black reference curve provides an estimate of the NTV for each applied field.
represent repeat discharges, showing the shot-to-shot reproducibility of the results. The vertical separation between the colored curves and black reference curve provides an estimate of the NTV for each applied field.
Figure 5. The neutral beam torque trajectories in rotation space of a reference discharge with no applied I-coil fields (black) and discharges with 4.3 kA n = 2 I-coil waveforms (color) defined by phasing 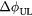 . The discharges are 153271 (black, reference), 153272 (blue,
. The discharges are 153271 (black, reference), 153272 (blue,  ), 153265 (green,
), 153265 (green,  ), 153276 (red,
), 153276 (red, 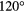 ), 153279 (orange,
), 153279 (orange, 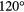 ), 153275 (cyan,
), 153275 (cyan, 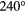 ), and 153273 (purple,
), and 153273 (purple, 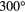 ).
).
Download figure:
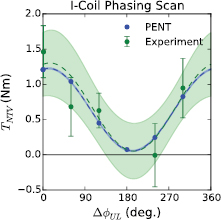
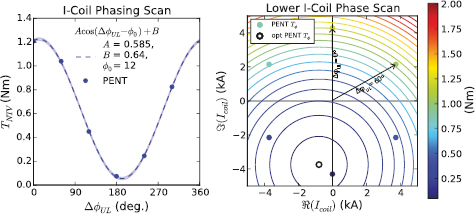
Standard image High-resolution imageThe phasing dependence of the measured NTV torque is shown in figure 6. The torque is taken from the difference in NBI torques at the edge rotation 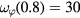 krad s−1; a rotation with large nonaxisymmetric effects well away from the discharge endpoints and possible influences of resonant braking at low rotation. At this rotation, the NTV measurements show a sinusoidal dependence on the poloidal spectrum. The envelope of a least squares fit error analysis is shown to provide a sense of the accuracy of this description. The five phasings obtained in the experiment are enough to constrain the amplitude, offset, and phase of the sinusoid fit, and the major trends are clear despite significant experimental uncertainty. The analysis at
krad s−1; a rotation with large nonaxisymmetric effects well away from the discharge endpoints and possible influences of resonant braking at low rotation. At this rotation, the NTV measurements show a sinusoidal dependence on the poloidal spectrum. The envelope of a least squares fit error analysis is shown to provide a sense of the accuracy of this description. The five phasings obtained in the experiment are enough to constrain the amplitude, offset, and phase of the sinusoid fit, and the major trends are clear despite significant experimental uncertainty. The analysis at 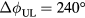 as well as a sinusoidal fit to the collected data show that it is possible to eliminate, to the extent of experimental uncertainty, the coupling of the I-coil fields to NTV torque. This sinusoid with negligible offset is the mark of the applied fields coupling and decoupling to a single plasma mode that drives NTV. Nonlinear NTV modeling at this rotation also shown in figure 6 agrees with this spectral dependence and the corresponding single mode model is discussed in detail in the following section. The main results (a maximum at
as well as a sinusoidal fit to the collected data show that it is possible to eliminate, to the extent of experimental uncertainty, the coupling of the I-coil fields to NTV torque. This sinusoid with negligible offset is the mark of the applied fields coupling and decoupling to a single plasma mode that drives NTV. Nonlinear NTV modeling at this rotation also shown in figure 6 agrees with this spectral dependence and the corresponding single mode model is discussed in detail in the following section. The main results (a maximum at  , and peak to valley ratio of order 10) are robust for edge rotations above 25 krad s−1. Below this, the experimental scatter increases due in part to a growing tearing mode while the fitted torque becomes uncorrelated or insensitive to the phasing as evidenced by the convergence of many lines in figure 5 near 20 krad s−1.
, and peak to valley ratio of order 10) are robust for edge rotations above 25 krad s−1. Below this, the experimental scatter increases due in part to a growing tearing mode while the fitted torque becomes uncorrelated or insensitive to the phasing as evidenced by the convergence of many lines in figure 5 near 20 krad s−1.
Figure 6. The PENT prediction of the torque (blue) compared to the experimental values (green) as a function of lower I-coil phase. The dashed lines and shaded regions of similar color indicate least-squares sinusoidal fits and their error.
Download figure:
Standard image High-resolution imageAn unanticipated observation from the experiment was a general decrease in the NTV torque as the edge rotation approaches zero. This can be seen in the convergence of the reference NBI torque with the phase scan trajectories in figure 5 near zero rotation, where all but one of the error bars overlap. Previous results in DIII-D QH-mode plasmas observed a NTV peak between the neoclassical offset and zero rotation [5, 38], but the associated bifurcation of the torque balance is not discernible here. The large error bars near zero rotation do not rule out this behavior, but prevent any conclusions from being drawn in this region. Instead, the focus on of this analysis is on the smooth rotation space evolution where there is clear separation of torques beyond the errors, away from low rotation where bifurcations (as well as resistive MHD modes) might appear. The previous results, however, were associated with the super-banana plateau regime [9, 39] in which the electric precession frequency is much smaller than the magnetic precession. The next section will discuss the cross regime NTV modeling of the plasmas used here, showing that their kinetic profiles make them susceptible to a different set of kinetic resonances than the previous studies.
3. Modeling of the NTV coupling
Modeling of the experiments in DIII-D show that the integral NTV torque can be dominated by the coupling of applied fields to a single spectrum in these QH-mode plasmas. This spectrum, deemed the dominant mode for the NTV torque, is similar to the dominant mode for the resonant plasma response found in the Ideal Perturbed Equilibrium Code (IPEC) but not identical. This is because the plasma response to applied nonaxisymmetric fields in high beta discharges is dominated by the coupling to the pressure driven kink, the excitation of which drives both resonant and nonresonant torques. This section will first address full nonlinear PENT modeling in QH-mode plasmas that shows this single mode dependence. It will then show the close relation to the IPEC dominant mode overlap, providing the physics basis for the use of this simple linear metric in determining the optimal NTV coupling. The goal is not to validate of the detailed internal torque profile, but to provide a physics basis on which the practical single mode control observed in experiment can be understood. Applications of this model are discussed in the following section.
3.1. Nonlinear prediction dominated by coupling to a single mode
The PENT code, in conjunction with IPEC, was used to model the dependence of the NTV torque in the QH-mode plasmas discussed above on the applied poloidal spectrum. The combined NTV theory modeled in PENT makes use of the bounce averaged drift kinetic equation, and describes the resulting torque in a general form [12],

with,

Here, R0 is the major radius of the magnetic axis, B0 is the magnitude of the magnetic field on axis, N is the species density, T is the species temperature, ψ is the poloidal flux, 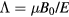 is a normalized magnetic moment, and ε is a temperature normalized energy. The resonance operator
is a normalized magnetic moment, and ε is a temperature normalized energy. The resonance operator  , normalized bounce frequency
, normalized bounce frequency 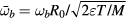 and normalized perturbed action
and normalized perturbed action 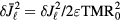 are unit-less quantities.
are unit-less quantities.
This model is used for its generality, including many common features of the NTV torque that make its prediction difficult in tokamak plasmas. The model includes the treatment of multiple collisionality regimes, strong drift orbit resonances, and rotational scalings. These, however, are not the focus of this paper. More fundamentally, it includes the inherent nonlinearity of the NTV torque (by any model) in the quadratic dependence on the perturbed action (proportional to the perturbed field in a circular large-aspect ratio approximations). This results in poloidal mode coupling, means that the torque from two sources of perturbation in not the sum of the torque from each source individually, and suggests a sensitivity to perturbed mode structures far more complicated than commonly optimized resonant coupling. This section, however, shows that a single mode model can be used to effectively describe the NTV torque in the plasmas of interests without sacrificing the generality of the NTV physics.
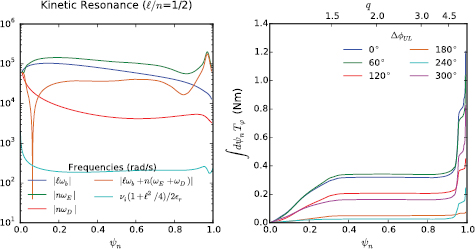
Equilibria properties used in the model were taken from the middle of the torque ramp, corresponding to a period of rotation used in the experimental analysis of the phasing dependence. The input equilibrium was taken from shot 153276 (a representative case with roughly half the maximum observed torque) and the applied fields varied in the model as in the experiment. The QH-mode kinetic profiles during this period were characterized by strong rotation, with electric precession frequencies approaching the typical bounce frequency of trapped particles and much larger than the magnetic precession. The large aspect ratio approximations of these frequencies [11], and the effective Krook collision operator used in PENT are shown in figure 7. The kinetic precession resonance term is much larger than the collisionality, placing the majority of the plasma in the 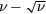 regime [9, 40, 41]. The integral torque, also shown in figure 7, is dominated by large NTV in the edge region. This region contains the highest perturbed fields and largest displacements in the perturbed equilibrium. The sharp spikes in the NTV, are additionally amplified by a strong
regime [9, 40, 41]. The integral torque, also shown in figure 7, is dominated by large NTV in the edge region. This region contains the highest perturbed fields and largest displacements in the perturbed equilibrium. The sharp spikes in the NTV, are additionally amplified by a strong  bounce harmonic resonance. These characteristics are important, as they emphasize the model is fully capturing the complex geometric dependencies and kinetic resonances, but are not explicitly tested here. Instead, we focus on the recovery of a simple dependence of the total torque on the applied field despite the presence or lack of complexity in the profile.
bounce harmonic resonance. These characteristics are important, as they emphasize the model is fully capturing the complex geometric dependencies and kinetic resonances, but are not explicitly tested here. Instead, we focus on the recovery of a simple dependence of the total torque on the applied field despite the presence or lack of complexity in the profile.
Figure 7. Left: The reduced large aspect ratio approximations of the bounce frequency (blue), electric precession (green), magnetic precession (red), and sum kinetic resonance term (orange) compared to the collisionality (cyan) profile in normalized flux for shot 153276. Right: The modeled torque density profile calculated in this equilibrium by PENT for applied fields from the I-coils with 6 upper–lower phasing values.
Download figure:
Standard image High-resolution imageThe integral torque modeled by the PENT code has a sinusoidal dependence on the phasing between IU and IL arrays, shown in figure 8. The points represent modeled torque using the experimental n = 2 current amplitudes and the 6 lower I-coil phases attempted in the experiment, fixing  . These are then used in a least squares fit of a sinusoid with amplitude, offset, and phase as the free parameters. The quality of the fit for the input profiles is clear from figure 8, which includes a shaded band corresponding to the uncertainty of the fit function. Note that this result includes only the n = 2 perturbations. While n = 2 coil waveforms are known to produce n = 4 sidebands in DIII-D [42], modeling found the torque produced by the sidebands to be well over an order of magnitude below the n = 2 torque as has been found in forward-Ip EFC experiments [43]. Varying the rotation profile in the experimentally realized range above 25krad/s varies the amplitude of the modeled torque by ±20%, remaining comparable to the experimental result within the experimental uncertainty. The main result is the qualitative, single mode, sinusoidal behavior that is recovered by the model, not the exact amplitude. The model shows that maximum n = 2 torque can be obtained in these plasmas using
. These are then used in a least squares fit of a sinusoid with amplitude, offset, and phase as the free parameters. The quality of the fit for the input profiles is clear from figure 8, which includes a shaded band corresponding to the uncertainty of the fit function. Note that this result includes only the n = 2 perturbations. While n = 2 coil waveforms are known to produce n = 4 sidebands in DIII-D [42], modeling found the torque produced by the sidebands to be well over an order of magnitude below the n = 2 torque as has been found in forward-Ip EFC experiments [43]. Varying the rotation profile in the experimentally realized range above 25krad/s varies the amplitude of the modeled torque by ±20%, remaining comparable to the experimental result within the experimental uncertainty. The main result is the qualitative, single mode, sinusoidal behavior that is recovered by the model, not the exact amplitude. The model shows that maximum n = 2 torque can be obtained in these plasmas using 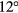 phasing, while the spectrum produced by
phasing, while the spectrum produced by 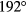 phasing has minimal coupling to the torque. The difference in extrema shows the importance of the poloidal spectra, as the applied torque can vary by an order of magnitude.
phasing has minimal coupling to the torque. The difference in extrema shows the importance of the poloidal spectra, as the applied torque can vary by an order of magnitude.
Figure 8. Left: The PENT code modeled torque (circles) fit a sinusoid (dashed line and shaded error) with respect to phasing. These models include poloidal mode coupling, general geometric shaping and aspect ratio, intermediate regimes and bounce harmonic resonances. Right: The modeled torques, indicated by color, fit to circular contours (solid lines) in the complex coil current phase space defined by the real and imaginary components of the applied n = 2 lower I-coil waveform. The center of these contours is indicated as a black circle. Note that the constant upper I-coil field is a hidden variable in this figure.
Download figure:
Standard image High-resolution imageThe phasing scan can be mapped to a two dimensional phase space of the complex lower I-coil current 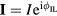 . As the scan was done at constant amplitude, the modeled points lie on a circular contour in this phase space and the sinusoidal dependence of the torque in
. As the scan was done at constant amplitude, the modeled points lie on a circular contour in this phase space and the sinusoidal dependence of the torque in 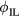 corresponds to the intersection of this contour with circular contours of constant torque quadratically approaching their centroid extremum.
corresponds to the intersection of this contour with circular contours of constant torque quadratically approaching their centroid extremum.
Figure 8 shows IL phase space contours of the torque described by,
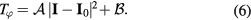
The scan defined by a constant amplitude I and varied phase ϕ is described by the family of phase space vectors,  , while the extremum is given by constant amplitude and phase,
, while the extremum is given by constant amplitude and phase, 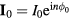 . Inserting these into equation (6), the dependence is reduced to the simple sinusoid,
. Inserting these into equation (6), the dependence is reduced to the simple sinusoid,

with amplitude 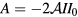 , phase
, phase 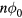 and offset
and offset  shown in the corresponding plot on the left.
shown in the corresponding plot on the left.
3.2. Relation to resonant coupling
IPEC calculates the linear plasma response to external nonaxisymmetric fields, allowing superposition of the plasma response fields. Extensive sensitivity studies have been performed using the IPEC model for n = 1 resonant locking thresholds [18, 19, 44]. Although the ideal model does not capture the field penetration physics, the resonant component suppressed by shielding currents prior to penetration is readily obtainable. The linear coupling between resonant components and spectra applied to a control surface (taken to be the plasma surface) in IPEC can be expressed by a linear matrix equation,

where 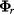 is a r-row vector containing the area normalized resonant field shielded by surface currents at each of the r resonant surfaces in the plasma,
is a r-row vector containing the area normalized resonant field shielded by surface currents at each of the r resonant surfaces in the plasma, 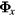 is a m-row vector representing the m applied spectral components on the control surface given by equation (9), and elements of the coupling matrix
is a m-row vector representing the m applied spectral components on the control surface given by equation (9), and elements of the coupling matrix 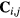 are the linear coefficients relating applied poloidal spectrum to the resultant resonant components. Here, the resonant components contain both the applied vacuum field and the plasma response.
are the linear coefficients relating applied poloidal spectrum to the resultant resonant components. Here, the resonant components contain both the applied vacuum field and the plasma response.
Fourier decomposition of the area weighted spectrum is defined as,

where S is a flux surface with area A and unit normal  ,
,  is the externally applied field. The spectral components
is the externally applied field. The spectral components 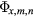 have units of flux and are independent of the choice of magnetic coordinates
have units of flux and are independent of the choice of magnetic coordinates 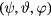 corresponding to the Jacobian
corresponding to the Jacobian 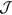 .
.
Singular value decomposition of the coupling matrix 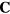 gives eigenvectors
gives eigenvectors 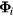 and eigenvalues
and eigenvalues 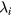 of
of 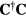 , ranked by the energy content of the resonant response to the applied spectrum. The first eigenvalue is regularly an order of magnitude above the next highest [17, 45], indicating the dominance of the corresponding eigenspectrum
, ranked by the energy content of the resonant response to the applied spectrum. The first eigenvalue is regularly an order of magnitude above the next highest [17, 45], indicating the dominance of the corresponding eigenspectrum 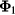 . The magnitude of the resonant response is then well defined by the extent to which an applied spectrum overlaps with the dominant mode. That is, the resonant coupling is proportional to the overlap parameter,
. The magnitude of the resonant response is then well defined by the extent to which an applied spectrum overlaps with the dominant mode. That is, the resonant coupling is proportional to the overlap parameter,

The validity of the single dominant mode approximation is confirmed for the QH-mode plasmas used here, by a ratio of the first eigenvalues 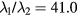 . The poloidal spectrum of the dominant mode is shown in figure 2. Figure 9 shows the square of the overlap exhibits sinusoidal dependence on the phasing similar to the torque and thus a similar circular contour mapping in the phase space of the lower I-coil array. The sinusoid is a direct consequence of the quadratic definition (10) evaluated on the single control surface, and the near-zero minimum the mark of a single dominant mode. The phase of the overlap contour extremum is determined by the phasing of I-coils that best overlaps the IPEC ideal MHD dominant mode, and agrees with that of the NTV extremum despite no explicit rotation dependence or other neoclassical kinetic physics. This suggests that the ideal MHD dominant mode structure is well coupled to the nonambipolar transport and torque. The IPEC dominant mode is not exactly the mode structure best coupled to the NTV, as evidenced by the fact that the extremum I-coil current amplitude is slightly larger. However, the quadratic nature of equation (6) has produced a shallow and broad well near the single mode optima. The difference between the NTV calculated by PENT at the two optima is 1% of the phase scan sinusoidal amplitude, confirming that the ideal MHD calculation is a close proxy for the NTV dominating mode.
. The poloidal spectrum of the dominant mode is shown in figure 2. Figure 9 shows the square of the overlap exhibits sinusoidal dependence on the phasing similar to the torque and thus a similar circular contour mapping in the phase space of the lower I-coil array. The sinusoid is a direct consequence of the quadratic definition (10) evaluated on the single control surface, and the near-zero minimum the mark of a single dominant mode. The phase of the overlap contour extremum is determined by the phasing of I-coils that best overlaps the IPEC ideal MHD dominant mode, and agrees with that of the NTV extremum despite no explicit rotation dependence or other neoclassical kinetic physics. This suggests that the ideal MHD dominant mode structure is well coupled to the nonambipolar transport and torque. The IPEC dominant mode is not exactly the mode structure best coupled to the NTV, as evidenced by the fact that the extremum I-coil current amplitude is slightly larger. However, the quadratic nature of equation (6) has produced a shallow and broad well near the single mode optima. The difference between the NTV calculated by PENT at the two optima is 1% of the phase scan sinusoidal amplitude, confirming that the ideal MHD calculation is a close proxy for the NTV dominating mode.
Figure 9. Left: The IPEC overlap (green circles) fit to a sinusoid (dashed line and shaded error) with respect to phasing. Right: The overlap, indicated by color, is described by circular contours in the lower I-coil phase space. The center of these contours (black circle) corresponds to the minimum coupling of the applied field to the IPEC dominant mode.
Download figure:
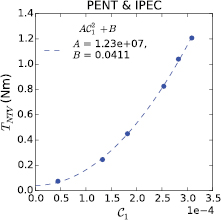
Standard image High-resolution imageThe quality of the overlap as a metric parameterizing the nonresonant torque is apparent in the quality of a quadratic fit of the points in the phasing scan shown in figure 10. The nonlinear torque is well correlated with the square of the linear metric in these QH-mode plasmas. This is expected, as the high 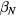 results in perturbations dominated by the plasma response. The dominant mode plasma response being proportional to the overlap, the torque can then be approximated as proportional to the square of the overlap through a common large aspect ratio simplification of the variation in the action
results in perturbations dominated by the plasma response. The dominant mode plasma response being proportional to the overlap, the torque can then be approximated as proportional to the square of the overlap through a common large aspect ratio simplification of the variation in the action  [11]. Note that this approximation provides insight into the expected relationship, but the full perturbed action including arc-length change, energy and pitch angle dependences was used in the PENT modeling presented.
[11]. Note that this approximation provides insight into the expected relationship, but the full perturbed action including arc-length change, energy and pitch angle dependences was used in the PENT modeling presented.
Figure 10. The nonlinear torque calculated using the PENT code (circles) fit to a quadratic dependence (dashed line) on the IPEC overlap metric for the six point phasing scan of the I-coils.
Download figure:
Standard image High-resolution imageThe IPEC overlap parameter is sometimes used as a proxy for coupling to the least stable plasma Kink, a global MHD mode with predictable structure. This approximation is valid in the limit of high β (the ratio of plasma pressure to magnetic pressure) and strong shaping, in which the global plasma response is dominated by the least stable kink mode. In these plasmas, this mode is a pressure driven kink with a common large wavelength ballooning structure near the low field side (LFS) mid-plane that dominates the plasma response. Similar LFS structure has been found to be a common characteristic of the IPEC dominant mode in many high performance regimes and tokamaks [17, 45, 46].
Note that plasmas in DIII-D that have been observed to have a multi-modal response to n = 2 fields have had less spacing in the SVD eigenvalues as well as significant High Field Side (HFS) plasma response [47, 48]. The poloidal field sensors used to measure the HFS response in multi-modal experiments measure signals at or near the noise floor of ∼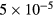 T in these plasmas, which is much lower than the measured LFS response maximum of ∼
T in these plasmas, which is much lower than the measured LFS response maximum of ∼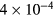 T. This confirms the single modal description of these plasmas in this new metric as well as the largely LFS nature of the response.
T. This confirms the single modal description of these plasmas in this new metric as well as the largely LFS nature of the response.
The maximized resonant perturbations associated with the IPEC dominant mode are associated with the NTV torque as well. The first reason for this association is that this response excites a large plasma amplification of the applied fields, maximizing the total perturbed field. There are more subtle reasons, however, to expect the coupling of the particular kink excited by the IPEC dominant mode and NTV torque.
Although NTV is often associated with 'nonresonant' perturbations, it is the field-aligned modulations and not the perpendicular components that drive NTV torque [11]. As described above, the application of fields aligned with the dominant mode result in the largest resonant response at rational surfaces sampling the entirety of the plasma volume. This naturally results in the very pitch-aligned perturbations throughout the plasma volume that are responsible for NTV. Furthermore, both the reduced large-aspect-ratio approximation of PENT's semi-analytic model and full particle simulations using POCA have demonstrated that field-orbit alignment leads to peaking of the NTV near  [49]. Particles near these rationals repeatedly sample the same field distortion without phase mixing, leading to rapid nonambipolar transport and large torques. That is, the fields maximized by the dominant mode also have maximum effectiveness in driving NTV torque.
[49]. Particles near these rationals repeatedly sample the same field distortion without phase mixing, leading to rapid nonambipolar transport and large torques. That is, the fields maximized by the dominant mode also have maximum effectiveness in driving NTV torque.
Figure 11 shows the field-aligned modulation of the field modeled by IPEC for 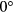 and
and 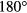 phasing, corresponding to large and low overlap with the dominant mode respectively. The large resonant response at the rational surfaces in the
phasing, corresponding to large and low overlap with the dominant mode respectively. The large resonant response at the rational surfaces in the  case clearly create a pitch-aligned kink throughout the plasma. The largest amplitudes are inside the inner most rational (q = 3/2) and at the plasma edge, which is where figure 7 confirms the majority of the torque is. The
case clearly create a pitch-aligned kink throughout the plasma. The largest amplitudes are inside the inner most rational (q = 3/2) and at the plasma edge, which is where figure 7 confirms the majority of the torque is. The 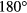 case, despite having the same energy in the coils, drives very little pitch aligned field and results in very low NTV torque.
case, despite having the same energy in the coils, drives very little pitch aligned field and results in very low NTV torque.
Figure 11. Poloidal cross section of the perturbed field model by IPEC for 4.3 kA n = 2 I-coils with upper–lower phasing 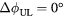 and
and 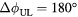 . The total (vacuum + plasma response) Lagrangian perturbation used in the PENT NTV model is shown.
. The total (vacuum + plasma response) Lagrangian perturbation used in the PENT NTV model is shown.
Download figure:
Standard image High-resolution imageNote that the perturbations shown in figure 11 are weighted towards the LFS. In the common regimes, the torque is dominated by trapped particles that execute banana orbits bouncing across the field minimum on the LFS [8, 9, 11]. All these particles thus sample the perturbations near the LFS mid-plane, while only a subset of weakly trapped particles sample perturbations on the HFS. The deeply trapped particles are especially susceptible as they sample the same unbalanced perturbation many times at high frequency.
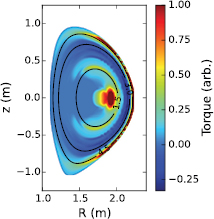
The combined NTV theory modeled in PENT makes use of the bounce averaged drift kinetic equation, and describes the resulting torque as a flux function. Some sense of the relative importance of poloidal positions can be obtained by plotting the torque flux density 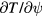 as a cumulative integral in pitch angle. From equation (19) in [12], this quantity can be written as,
as a cumulative integral in pitch angle. From equation (19) in [12], this quantity can be written as,
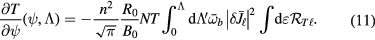
Figure 12 shows the this quantity for one of the cases modeled above mapped to  using the poloidal bounce points determined by
using the poloidal bounce points determined by  . The color thus represents the amount of NTV torque coming from particles that have sampled the perturbations in that region. Radially, the contour shows torque concentrated inside the q = 3/2 surface and outside the q = 9/2 surface as was seen in figure 7 and is expected from the perturbations in figure 11. The additional poloidal information indicates that the LFS mid-plane is the most important region in the plasma for NTV. Note that this example is from a phasing that is nearly de-coupled from the dominant mode, which produced a plasma response concentrated more heavily away from the LFS extremum. The case of the maximum NTV coupling with a large LFS mid-plane plasma response looks similar, confirming the rigidity of the distribution expected in a single mode model. This LFS weighting helps facilitate the coupling of the applied field structure to the NTV, although the amplification of the parallel fields by the plasma response is expected to be of primary importance.
. The color thus represents the amount of NTV torque coming from particles that have sampled the perturbations in that region. Radially, the contour shows torque concentrated inside the q = 3/2 surface and outside the q = 9/2 surface as was seen in figure 7 and is expected from the perturbations in figure 11. The additional poloidal information indicates that the LFS mid-plane is the most important region in the plasma for NTV. Note that this example is from a phasing that is nearly de-coupled from the dominant mode, which produced a plasma response concentrated more heavily away from the LFS extremum. The case of the maximum NTV coupling with a large LFS mid-plane plasma response looks similar, confirming the rigidity of the distribution expected in a single mode model. This LFS weighting helps facilitate the coupling of the applied field structure to the NTV, although the amplification of the parallel fields by the plasma response is expected to be of primary importance.
Figure 12. The torque density cumulative pitch angle integral function mapped to the plasma cross section at the bounce points determined by the pitch variable. The case shown is taken from the  case used for the phasing scan modeling. Surfaces with safety factor q = 3/2, 6/2, and 9/2 are shown in black for reference.
case used for the phasing scan modeling. Surfaces with safety factor q = 3/2, 6/2, and 9/2 are shown in black for reference.
Download figure:
Standard image High-resolution image4. Discussion and conclusions
When using the phasing of two nonaxisymmetric coil arrays to vary the poloidal spectrum applied to QH-mode plasmas, the measured torque and modeling are consistent with a single mode model. This single mode behavior is defined by a sinusoidal phasing dependence with negligible offset from zero at the minimum. Both the full nonlinear PENT predication and the linear IPEC dominant mode prediction of the maximum NTV coupling are within the error of the experimentally determined phasing offset  . Allowing for amplitude as well as phase changes in the lower I-coil array, the corresponding extrema are clustered in the two dimensional phase space. Figure 13 shows the phase space map produced using the experimental measurement, as well as the minima fit using the PENT prediction and dominant mode proxy. Both model minima lie within a shallow bowl of the phase space map fit to the experimental data. The map extrapolates the NTV at these other optima to be 0.11 Nm and 0.18 Nm respectively, each differing from the 0.07 Nm experimental minimum by less than 8% of the 1.32 Nm peak in the sinusoidal fit to the experimental torque. This difference between the extrapolated NTV at each model minimum is within the error bar on any given torque measurement (∼0.4Nm), making either a sufficient choice for minimal rotation drive within the accuracy of this experiment.
. Allowing for amplitude as well as phase changes in the lower I-coil array, the corresponding extrema are clustered in the two dimensional phase space. Figure 13 shows the phase space map produced using the experimental measurement, as well as the minima fit using the PENT prediction and dominant mode proxy. Both model minima lie within a shallow bowl of the phase space map fit to the experimental data. The map extrapolates the NTV at these other optima to be 0.11 Nm and 0.18 Nm respectively, each differing from the 0.07 Nm experimental minimum by less than 8% of the 1.32 Nm peak in the sinusoidal fit to the experimental torque. This difference between the extrapolated NTV at each model minimum is within the error bar on any given torque measurement (∼0.4Nm), making either a sufficient choice for minimal rotation drive within the accuracy of this experiment.
Figure 13. The phase space map determined from a single mode model fit to experimental measurements of the NTV torque. The torque is indicated by color for the five experimental points in the lower I-coil phase space. Solid lines indicate contours of constant torque determined by a least-squares fit to equation (6). The fit minimum (black circle) is similar to minima from single mode fits of the torque predictions from PENT (black star) and IPEC dominant mode overlap (black X).
Download figure:
Standard image High-resolution imageThe circular IL phase space torque contours given by equation (6) with negligible offset specify that the torque is determined by the coupling to a single poloidal spectrum, minimized by the relative combination of I-coils corresponding to the contour centroid 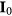 . This is a single mode model, and represents a major simplification of the analysis necessary to compute the applied torque. The NTV torque, computed from first principles, is nonlinear with respect to the magnetic spectrum due to poloidal mode coupling that occurs in the squared variation of the action. The torque from multiple sources cannot be linearly summed, and complete profile computations must be performed for every new combination of sources. The single mode model makes it possible to map the torque throughout the phase space of multiple sources using a finite number of computations. For the experiment described here, a minimum of 4 independent IL current distributions are enough to solve for the variables
. This is a single mode model, and represents a major simplification of the analysis necessary to compute the applied torque. The NTV torque, computed from first principles, is nonlinear with respect to the magnetic spectrum due to poloidal mode coupling that occurs in the squared variation of the action. The torque from multiple sources cannot be linearly summed, and complete profile computations must be performed for every new combination of sources. The single mode model makes it possible to map the torque throughout the phase space of multiple sources using a finite number of computations. For the experiment described here, a minimum of 4 independent IL current distributions are enough to solve for the variables  and map the torque across the entire space of possible IL-IU current combinations. This extension, from modeling singular points in an infinite space to efficiently mapping the entire space, empowers NTV models to execute feedforward optimizations of the nonaxisymmetric field sources for a wide variety of desirable applications.
and map the torque across the entire space of possible IL-IU current combinations. This extension, from modeling singular points in an infinite space to efficiently mapping the entire space, empowers NTV models to execute feedforward optimizations of the nonaxisymmetric field sources for a wide variety of desirable applications.
This paper introduces the reduction of NTV application to a single mode model in the context of optimal rotation drive perturbing an originally axisymmetric equilibrium rotating in the direction of the ion neoclassical offset rotation. It is more common, however, that the DIII-D tokamak is operated with plasmas rotating in the co-current direction opposite that of the neoclassical offset. Any intrinsic nonaxisymmetric perturbations in the machine then cause rotation braking that tends to deteriorate of the stability and confinement. The field sources of interest are thus the intrinsic error field and the EFC coil arrays. The optimal operating point is usually defined as the combination that minimizes the NTV torque. The process of finding such an optimum is identical to that of finding the NTV in the phase space models presented here. In fact, these are intended as a direct parallel to EFC mappings used for many years at DIII-D [19, 20, 50, 51]. The extremum presented here, can be viewed as the 'correction' of the upper I-coil array n = 2 field by the lower I-coil array. It could also be compared to a stellarator-like optimization, for which applied nonaxisymmetries drive no neoclassical transport. In this scenario, however, the NTV drives rotation and the optimum is thus the maximum torque obtained by applied fields 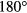 from the extremum phase.
from the extremum phase.
Extensive work has been done showing that the IPEC overlap is an accurate metric for error field penetration thresholds and extending the technique to future devices error field correction [17, 18, 45, 52]. The alignment of the dominant NTV mode and the IPEC dominant mode is a consequence of close coupling of the dominant kinetic transport to this dominant MHD response. Specifically, the application of the IPEC dominant mode external fields results in a global kink, with large field-aligned modulations that drive nonambipolar transport and NTV torque. This close relationship between the dominant mode metric and the ultimate NTV driving fields is not specific to any one NTV model, and is expected to be robust across a wide range of regimes. It may be used to explain, for example, why momentum loss is correlated with the dominant mode metric rather than the maximum measured plasma response in recently observed multi-modal plasmas [47].
The reduction of NTV to a single mode model enables the extension of well established linear EFC optimization techniques [16, 21, 45, 46, 52, 53] to regimes where the resonant physics is not necessarily the dominant concern. In these regimes the non-resonant, in addition to the resonant, harmonics of the single dominant mode directly impact the plasma rotation through the NTV. The results presented here use the NTV single mode model to efficiently map the induced torque as a function of multiple nonaxisymmetric field sources in regimes where the NTV is expected to be the dominant effect of the error field. In DIII-D, this includes fast rotating H-mode plasmas and spectra with toroidal mode number greater than 1.
Acknowledgments
This work was supported by the U.S. Department of Energy Office of Science Office of Fusion Energy Sciences using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Awards DE-FC02-04ER54698 and DE- AC02-09CH11466. The authors are grateful for the hard work of the entire DIII-D team, and of the Princeton collaboration headed by R. Nazikian that provided support for this work.