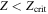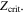FOLLOWING THE COSMIC EVOLUTION OF PRISTINE GAS. I. IMPLICATIONS FOR MILKY WAY HALO STARS

Our study makes use of ramses (Teyssier 2002), a cosmological AMR code, which uses an unsplit second-order Godunov scheme for evolving the Euler equations. ramses variables are cell centered and interpolated to the cell faces for flux calculations, which are then used by a Harten–Lax–van Leer–Contact Riemann solver (van Leer 1979; Einfeldt 1988). Self-gravity is solved using the multigrid method (Guillet et al. 2011) for all coarse levels in the simulation, and the conjugate gradient method is used for levels $\geqslant 11$. The code is capable of advecting any number of scalar quantities, defined as mass fractions, in each simulation cell. For example, the standard version of ramses evolves a mass fraction of metals for each cell, which may have contributions from Pop III stars and second-generation stars, referred to as total average metallicity $\overline{Z}$. As a simulation evolves, ramses creates star particles in regions of overdense gas, each of which represents hundreds to thousands of solar masses of individual stars. Like the gas, each such star particle is tagged with a ${\overline{Z}}_{\star }$ value, representing the average metallicity of the medium from which it was born.

We use these capabilities to generate and track new metallicity-related quantities for both the gas and star particles. For the gas, we introduce two new scalars: the average primordial metallicity, ${\overline{Z}}_{{\rm{P}}}$, and the pristine gas mass fraction, P. The primordial metallicity scalar, ${\overline{Z}}_{{\rm{P}}}$, tracks the mass fraction of metals generated by Pop III stars, which are likely to have nonsolar abundance ratios (Heger & Woosley 2002; Umeda & Nomoto 2003; Ishigaki et al. 2014). Our pristine gas fraction scalar models the mass fraction of gas with $Z\lt {Z}_{\mathrm{crit}}$, which allows us to track the process of metal mixing within each cell. While a cell may have a relatively high average metallicity, $\overline{Z}$, those metals are normally not well mixed throughout its volume at the time of injection. By tracking P, we can quantify the amount of pristine gas in such cells ($P\approx 1.0$) even if their mean metallicities are large.

Since we are primarily interested in the characteristics of stellar populations, we also track the pristine fraction and the primordial metallicity of each star particle (P_⋆ and ${\overline{Z}}_{{\rm{P}},\star }$, respectively). These values are adopted for each star particle from the gas in which it was formed. For example, a star particle born in a region of gas with P = 0.5 inherits ${P}_{\star }=0.5$ and represents a stellar population containing 50% pristine (Pop III) stars and 50% polluted stars, by mass. As P_⋆ is known for each star particle, when a star enriches the surrounding medium through SNe, we can determine the fraction of Pop III SN ejecta contributed, allowing us to track the primordial metallicity contributed by these stars. As such we are able to track the pollution of surrounding cells not only in terms of $\overline{Z}$ and P but also in terms of the cells' primordial metals, ${\overline{Z}}_{{\rm{P}}}$. As discussed in detail below, this allows us to connect assumptions about the yields from Pop III stars with observations of carbon-enhanced metal-poor (CEMP-no) stars (Beers & Christlieb 2005; Hansen et al. 2016; Yoon et al. 2016), which are defined as having [C/Fe] > +0.7 and [Ba/Fe] < 0.0 (Beers & Christlieb 2005). While Cooke & Madau (2014) and Sluder et al. (2016) attribute the abundances in CEMP stars to primordial, faint SNe and anisotropic ejecta, respectively, our method depends only on mixing and the abundance patterns of Pop III SNe.

By knowing the average metallicity, $\overline{Z}$, and the pristine gas fraction, P, we can better model the metallicity of the polluted fraction of gas (or stars). Since $\overline{Z}$ represents the average metallicity of a parcel of gas and the polluted fraction, ${f}_{\mathrm{pol}}\equiv 1-P$, models the fraction of gas that is actually polluted with metals, we can use the value of ${f}_{\mathrm{pol}}$ to predict the enhanced metallicity ($Z\gt \overline{Z}$) of the polluted fraction of gas in each simulation cell. This allows us to more accurately model the metallicity of the star particles created from this gas.

However, our new scalar only indicates that the pristine fraction of the cell contains gas with $Z\lt {Z}_{\mathrm{crit}}$. When considering primordial cells, we know that the pristine gas has $Z\approx 0$ and hence the polluted fraction, ${f}_{\mathrm{pol}}$, accounts for all of the metals in the cell. In this case we can use ${f}_{\mathrm{pol}}$ to precisely determine the enhanced metallicity of the polluted fraction of gas:

$$\begin{eqnarray}&&Z\equiv \displaystyle \frac{\overline{Z}}{{f}_{\mathrm{pol}}},\end{eqnarray} \tag{ 2 }$$

where Z is the enhanced metallicity of the polluted fraction of gas.

For instance, consider an initially primordial parcel of gas that is enriched, on average, to $\overline{Z}={10}^{-1}\,{Z}_{\odot }$ with $P=0.9\Rightarrow {f}_{\mathrm{pol}}=0.1$ by a nearby SN event. The fraction of stars subsequently produced from such gas will, ignoring possible differences in the star-forming efficiency between metal-free and polluted gas, be 90% pristine and 10% polluted. However, the metallicity of the polluted stars will be $10\times$ greater than the average metallicity since all of the metals in the cell are currently concentrated in 10% of its volume. Thus, in this case, we can simply correct the metallicity of star particles born in the gas by taking into account the polluted fraction of gas as described by Equation (2).

However, once mixing has reduced $P\lt 1.0$ with $\overline{Z}\gt {Z}_{\mathrm{crit}}$, it becomes possible for the average metallicity of a cell to fall to $\overline{Z}\lt {Z}_{\mathrm{crit}}$ either via the advection of pristine material from neighboring cells or via the movement of material with a lower average metallicity into the cell. Such cells' pristine fractions evolve back toward unity since mixing now dilutes areas with $Z\gt {Z}_{\mathrm{crit}}$ until the entire cell has P = 1.0 and $\overline{Z}=Z\lt {Z}_{\mathrm{crit}}$ throughout the cell. Now subsequent injections of pollutants can once again raise $\overline{Z}\gt {Z}_{\mathrm{crit}}$, but in this case not all of the metals are concentrated in the incoming pollutants.

Our scalar P does not encode the metallicity of the pristine gas: the scalar only captures the fraction of gas with $Z\lt {Z}_{\mathrm{crit}}$, and as such we do not know the fraction of metals, captured in the scalar $\overline{Z}$, that are distributed in the pristine fraction of gas. However, we can bound this value since we know that the metallicity of the polluted and pristine fractions of the gas must sum to the average metallicity of the cell. Equation (3) solves for the metallicity of the polluted fraction of gas, Z, when considering that the pristine fraction has an unknown metallicity ${Z}_{{\mathbb{P}}}$:

$$\begin{eqnarray}\overline{Z} & = & Z(1-P)+{Z}_{{\mathbb{P}}}P,\\ Z & = & \displaystyle \frac{\overline{Z}-{Z}_{{\mathbb{P}}}P}{(1-P)}.\end{eqnarray} \tag{ 3 }$$

It can be seen that when ${Z}_{{\mathbb{P}}}=0$ we recover $Z=\overline{Z}/{f}_{\mathrm{pol}}$, the enhanced metallicity of a polluted volume of gas within a primordial cell. This correction is the upper bound for the metallicity of the polluted fraction. We can also establish a lower bound for the polluted fraction's metallicity correction by considering the definition of the pristine fraction, namely, that ${Z}_{{\mathbb{P}}}\lt {Z}_{\mathrm{crit}}$. Substituting for ${Z}_{{\mathbb{P}}}$, this means that

$$\begin{eqnarray}&&Z=\displaystyle \frac{\overline{Z}-{Z}_{\mathrm{crit}}P}{(1-P)},\end{eqnarray} \tag{ 4 }$$

is a lower bound on the correction to the metallicity of the polluted fraction. Comparing the lower and upper bounds of the correction to the metallicity of the polluted fraction, we see that the term ${Z}_{\mathrm{crit}}P$ will have the largest effect when $\overline{Z}\approx {Z}_{\mathrm{crit}}$ and $P\approx 1$. This is depicted in Figure 1.

Zoom In Zoom Out Reset image size

The pristine gas fraction, P, is initialized to 1.0 for all cells in the simulation. As the first stars are formed and go SNe, metal-rich ejecta, along with entrained gas from the cell, is immediately carried into neighboring cells, where it increases the cell density from ${\rho }_{\mathrm{cell}}$ to ${\rho }_{\mathrm{cell}}+{\rho }_{\mathrm{ejecta}}$. This decreases the cell's pristine gas fraction from 1.0 to $P={\rho }_{\mathrm{cell}}/({\rho }_{\mathrm{cell}}+{\rho }_{\mathrm{ejecta}})$, starting the decay of P. We note that this method of computing the change to P assumes that the ejecta (with density ${\rho }_{\mathrm{ejecta}}$) is well mixed. The subgrid mixing algorithm is then invoked for each cell at each time step, resulting in the decay of the pristine gas fraction (based on theoretical modeling of the pristine fraction with physical parameters calibrated by numerical simulations, as described below) for all cells where $P\lt 1.0$.

Finally, we note that star formation is likely to be more efficient in polluted gas, due to more efficient cooling. However, given the uncertainties in the Pop III initial mass function (IMF), we have elected to weigh star formation rates (SFRs) in pristine and polluted gas only by the pristine gas fraction. For example, stars born in gas with P = 0.9 give rise to star particles with ${P}_{\star }=0.9$, meaning that 90% of the mass of the star particle represents Pop III stars. In Table 1 we clarify the notation used to describe the scalars we reference throughout this paper.

Table 1.  Notation

Symbol	Definition
P, P⋆	The mass fraction of gas (star particles) with $Z\lt {Z}_{\mathrm{crit}}$
${f}_{\mathrm{pol}}$	The mass fraction of gas or star particles with $Z\geqslant {Z}_{\mathrm{crit}}$; ${f}_{\mathrm{pol}}\equiv 1-P$
${Z}_{{\mathbb{P}}}$	The metallicity of the pristine fraction of gas or star particle;
	while undetermined, it is bounded by the range $0\leqslant {Z}_{{\mathbb{P}}}\leqslant {Z}_{\mathrm{crit}}$
$\overline{Z}$, ${\overline{Z}}_{{\rm{P}}}$ ${\overline{Z}}_{\star },{\overline{Z}}_{{\rm{P}},\star }$	The average metallicity (primordial metallicity) within an unmixed volume of gas (or star particle)
Z, ${Z}_{{\rm{P}}}$ ${Z}_{\star },{Z}_{{\rm{P}},\star }$	The corrected and assumed homogeneous metallicity (primordial metallicity) of the polluted fraction of gas (or star particle)

Download table as:  ASCIITypeset image

2.2.1. Self-convolution Model

The novelty of our approach is in how the pollution of pristine gas is modeled on subgrid scales. Here we rely on the work described in PS13, which determined that in fully developed turbulence, the pollution rate can be modeled by a relatively simple self-convolution model. While SN forcing is intuitively compressive, P13 used solenoidal forcing to drive turbulence. However, studies by Federrath et al. (2010) and Padoan et al. (2016) demonstrate that SN driving forces are not purely compressive. Indeed, the effective SN driving force may possibly be more solenoidal than compressive with a compressive-to-solenoidal ratio below 1, due to the nonsphericity of the SN blast, which tends to be clumpy in both velocity and density space. Additionally, each "SN" in our simulation represents the combined energy of several SNe since each star particle represents a Salpeter IMF with a total mass in the range of $726\mbox{--}3628\,{M}_{\odot }$. These considerations conspire to make the ISM highly turbulent. While compressive forcing is surely a part of SN-driven turbulence, results from simulations using solenoidally driven turbulence are a reasonable approximation when determining the mixing timescales for SN-driven turbulence.

There has been compelling evidence that in a turbulent medium, the dominant scalar structures at small scales are two-dimensional sheets or edges (e.g., Pan & Scannapieco 2011), and the rate at which these sheets are produced is determined mainly by the turbulent stretching rate at large length scales. With time, the sheets become thinner, and once their thickness is sufficiently small for molecular diffusivity to efficiently operate, neighboring sheets are homogenized, leading to a reduction in the width of the local metallicity probability distribution function, ${\rm{\Phi }}(Z;t)$.

The evolution of ${\rm{\Phi }}(Z;t)$ within a turbulent region in this physical picture can be approximately described as

$$\begin{eqnarray}\displaystyle \frac{\partial {\rm{\Phi }}(Z;t)}{\partial t} & = & s(t)\left[-{\rm{\Phi }}(Z;t)+{\displaystyle \int }_{0}^{1}{{dZ}}_{1}{\rm{\Phi }}({Z}_{1};t)\right.\\ & & \times \left.{\displaystyle \int }_{0}^{1}{{dZ}}_{2}{\rm{\Phi }}({Z}_{2};t)\times \delta \left(Z-\displaystyle \frac{{Z}_{1}+{Z}_{2}}{2}\right)\right],\end{eqnarray} \tag{ 5 }$$

where s(t) is the turbulent stretching rate that controls the rate at which the probability density function (PDF) convolution proceeds (Curl 1963; Dopazo 1979; Janicka et al. 1979). Extending this model, Venaille & Sommeria (2007) developed a "continuous" version, which essentially assumes that the convolution occurs everywhere in the flow at any given time, but in an infinitesimal time, ${\rm{\Delta }}t$, the number of convolutions is infinitesimal and equal to $\epsilon =s(t){\rm{\Delta }}t$. Duplat & Villermaux (2008) then generalized this even further, including a parameter n such that a fraction $n\epsilon$ of the flow experiences mixing events during a time interval, ${\rm{\Delta }}t$, and the number of convolutions in this fraction of the flow is 1/$n.$ In this model, n characterizes the degree of spatial locality of the PDF convolution, with larger values of n corresponding to more global convolutions. The models of Curl (1963) and Venaille & Sommeria (2007) correspond to n = 1 and $n\to \infty$, respectively.

By integrating ${\rm{\Phi }}(Z;t)$ from a finite but extremely small value up to the critical metallicity, the Duplat & Villermaux (2008) model can be used to derive a very simple equation for the evolution of the $Z\lt {Z}_{\mathrm{crit}}$ pristine fraction:

$$\begin{eqnarray}&&\displaystyle \frac{{dP}}{{dt}}=-\displaystyle \frac{n}{{\tau }_{\mathrm{con}}}P(1-{P}^{1/n}).\end{eqnarray} \tag{ 6 }$$

The n = 1 case of this equation was first given in Pan & Scalo (2007). This equation traces the evolution of P as a function of n and a timescale ${\tau }_{\mathrm{con}}$, and these parameters, in turn, are functions of the turbulent Mach number, M, and the average metallicity of the cell relative to the critical metallicity, $\overline{Z}/{Z}_{\mathrm{crit}}$ (Pan et al. 2012; PS13).

Note that Equation (6) has the property that if P = 1, then $\dot{P}=0$, ensuring that pristine cells remain pristine. There are no metals in such a cell with which to pollute it. As soon as the injection of polluted material causes $P\lt 1.0$, however, the polluted fraction will then continue to decrease. Including the cell-to-cell advection handled by ramses and the addition of enriched ejecta material to a cell, the full equation for the evolution of P is

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho P)}{\partial t}+{\boldsymbol{\nabla }}\cdot ({\boldsymbol{u}}\,\rho \,P)=-\displaystyle \frac{n}{{\tau }_{\mathrm{con}}}\rho P(1-{P}^{1/n})-{\dot{\rho }}_{\mathrm{ej}}P,\end{eqnarray} \tag{ 7 }$$

where ρ and ${\boldsymbol{u}}$ are the local density and velocity, respectively, and ${\dot{\rho }}_{\mathrm{ej}}$ is the rate that the density of cell is increased by the addition of ejecta. The reader may notice that we have omitted the diffusion term described by PS13 (Equation (49) in that work). We have not tried to characterize the numerical diffusion inherent in ramses, and a proper treatment would need to account for any difference between it and the diffusion term in PS13 when computing cell-to-cell diffusion. We leave this for a future work.

2.2.2. Locality Parameter and Convolution Timescale

The evolution of P described in Equations (6) and (7) depends on a convolution timescale, ${\tau }_{\mathrm{con}}$, and the parameter n, which quantifies the locality of mixing. Here we are interested in the case in which the driving scale of the turbulence and the length scale at which pollutants are added to the medium (referred to as L_f and L_p in PS13) both occur on the grid scale ${\rm{\Delta }}x.$ In this case, as shown in PS13, the locality parameter as a function of Mach number is well fit by

$$\begin{eqnarray}&&n=1+11\,\exp \left(-\displaystyle \frac{M}{3.5}\right).\end{eqnarray} \tag{ 8 }$$

This means that in subsonic turbulence, pollution is more of a global process, corresponding to $n\approx 12,$ and in highly supersonic turbulence pollution is more local, corresponding to $n\approx 1$, the n value in Curl's original model.

Also following PS13, we model the dynamical mixing time as

$$\begin{eqnarray}{\tau }_{\mathrm{con}}=\displaystyle \frac{{\rm{\Delta }}x}{{v}_{t}}\left\{\begin{array}{ll}{\tilde{\tau }}_{\mathrm{con}1} & \mathrm{if}\ {\rm{P}}\geqslant 0.9\\ {\tilde{\tau }}_{\mathrm{con}2} & \mathrm{if}\ {\rm{P}}\lt 0.9\end{array}\right.,\end{eqnarray} \tag{ 9 }$$

where v_t is the turbulent velocity of the cell and ${\tilde{\tau }}_{\mathrm{con}1}$ and ${\tilde{\tau }}_{\mathrm{con}2}$ account for the slightly less efficient mixing that occurs at low pollution fractions (PS13). Unlike n, these timescales depend not only on the Mach number but also on the ratio of the average metallicity in the turbulent region to the critical metallicity. For example, if the mean metallicity in the region is less than the critical metallicity, then the fraction of pristine material cannot monotonically decrease since complete mixing with $\overline{Z}\lt {Z}_{\mathrm{crit}}$ should imply P = 1.0. On the other hand, as PS13 were concerned only with cases in which the mean metallicity in the medium was much greater than the critical metallicity, their fits to the convolution timescale show only a weak dependence on $\overline{Z}/{Z}_{\mathrm{crit}}$. Using an extrapolation of the dependence $\overline{Z}/{Z}_{\mathrm{crit}}$ given in PS13 for $\overline{Z}/{Z}_{\mathrm{crit}}\lt 1.0$ results in P always decreasing—even when the average metallicity is subcritical.

Thus, we refit the dependence of ${\tilde{\tau }}_{\mathrm{con}1},$ ${\tilde{\tau }}_{\mathrm{con}2}$ on $\overline{Z}/{Z}_{\mathrm{crit}}$ working with the results of the PS13 data over a much larger range of values. Figure 2 depicts the normalized convolution timescale as a function of $\overline{Z}$ for the range of turbulent flows studied by PS13. For convenience we normalize to its value when ${Z}_{\mathrm{crit}}={10}^{-7}\,\overline{Z}$ as this value was used in the fits presented in PS13. As expected, the mixing time increases exponentially as $\overline{Z}$ approaches ${Z}_{\mathrm{crit}}$. As the critical metallicity in the simulations in PS13 was taken to be 10⁻⁷ of the mean metallicity, we define our fits in terms of the ratio

$$\begin{eqnarray}&&x\equiv -{\mathrm{log}}_{10}\left(\displaystyle \frac{\overline{Z}}{{10}^{7}{Z}_{\mathrm{crit}}}\right){\left[{\mathrm{log}}_{10}\left(\displaystyle \frac{\overline{Z}}{{Z}_{\mathrm{crit}}}\right)\right]}^{-1},\end{eqnarray} \tag{ 10 }$$

which equals zero when $\overline{Z}/{Z}_{\mathrm{crit}}={10}^{7}$ and approaches infinity as $\overline{Z}/{Z}_{\mathrm{crit}}$ drops to 1. We then obtained a simple fit to the PS13 simulation results as

$$\begin{eqnarray}{\tilde{\tau }}_{\mathrm{con}1} & = & \left[0.225-0.055\,\exp \left(-\displaystyle \frac{{M}^{3/2}}{4}\right)\right]\,\sqrt{\displaystyle \frac{x}{5}+1},\\ {\tilde{\tau }}_{\mathrm{con}2} & = & \left[0.335-0.095\,\exp \left(-\displaystyle \frac{{M}^{2}}{4}\right)\right]\,\sqrt{\displaystyle \frac{x}{3}+1},\end{eqnarray} \tag{ 11 }$$

if $\overline{Z}/{Z}_{\mathrm{crit}}\gt 1$, and ${\tau }_{\mathrm{con}}=\infty$ if $\overline{Z}/{Z}_{\mathrm{crit}}\leqslant 1$. It is possible for a region with $\overline{Z}\gt {Z}_{\mathrm{crit}}$ to evolve back to $\overline{Z}\leqslant {Z}_{\mathrm{crit}}$ due to the advection of highly pristine material from nearby cells. In this case we think of mixing as making the cell more pristine, rather than less, and evolve the pristine gas fraction back toward 1 as an exponential function of the cell's turbulent velocity:

$$\begin{eqnarray}&&\displaystyle \frac{d}{{dt}}(1-P)=-(1-P)\displaystyle \frac{{v}_{t}}{{\rm{\Delta }}x}.\end{eqnarray} \tag{ 12 }$$

Zoom In Zoom Out Reset image size

We note that the pristine fraction does not always evolve toward 1 immediately once $\overline{Z}\lt {Z}_{\mathrm{crit}}$. For example, if the polluted fraction in a cell is below $\overline{Z}/{Z}_{\mathrm{crit}}$, the average metallicity in the polluted region is still above ${Z}_{\mathrm{crit}}$, and thus the pristine fraction in the cell would still be decreasing as the polluted region mixes with more ambient pristine gas. Roughly speaking, only after the polluted fraction in a cell exceeds $\overline{Z}/{Z}_{\mathrm{crit}}$ does the pristine fraction start to evolve toward 1. However, accounting for this complexity by checking whether the polluted fraction in a cell is above or below $\overline{Z}/{Z}_{\mathrm{crit}}$ does not cause a significant difference from the results using Equation (12) immediately (when the average metallicity in a cell drops below ${Z}_{\mathrm{crit}}$). We will therefore focus on results from Equation (12).

All the fits above depend on the cells' turbulent velocity, v_t, and its ratio to the local sound speed, $M={v}_{t}/{c}_{s}.$ This velocity can be estimated in turn as ${v}_{{\rm{t}}}={\nu }_{{\rm{t}}}/{\rm{\Delta }}x,$ where ${\nu }_{{\rm{t}}}$ is the turbulent kinematic eddy viscosity of the scale of the cell, or as ${v}_{{\rm{t}}}=\sqrt{2K}$, where K is the subgrid kinetic energy. Many possible models exist in the literature for the estimate of v_t (e.g., Yoshizawa 1986; Moin et al. 1991; Erlebacher et al. 1992; Vreman et al. 1997) or K (e.g., Schumann 1975; Moeng 1984; Ghosal et al. 1995; Schmidt et al. 2006; Genin & Menon 2010; Scannapieco & Brüggen 2010; Chai & Mahesh 2012). While a comparison between different approaches merits further study, here we adopt the simplest approach, making use of the eddy viscosity model of Smagorinsky (1963). A brief overview of the approach used to compute v_t follows.

We first compute the numerical velocity gradients across each cell ${{\rm{\Delta }}}_{{\rm{i}}}{v}_{{\rm{j}}}$ to determine the local rate-of-strain tensor

$$\begin{eqnarray}&&{\rm{}}{S}_{\mathrm{ij}}\equiv \displaystyle \frac{1}{2}({{\rm{\Delta }}}_{{\rm{i}}}{v}_{{\rm{j}}}+{{\rm{\Delta }}}_{{\rm{j}}}{v}_{{\rm{i}}}),\end{eqnarray} \tag{ 13 }$$

which captures the 3D velocity shear around each cell (Sur et al. 2014). Starting with the energy in the Kolmogorov inertial spectrum (${\epsilon }^{2/3}{k}^{-5/3}$) and equating it to the loss of kinetic energy in the flow, $2\nu \langle {\rm{}}{S}_{{ij}}{\rm{}}{S}_{{ij}}\rangle$, we have the following:

$$\begin{eqnarray}&&2\nu \langle {\rm{}}{S}_{{ij}}{\rm{}}{S}_{{ij}}\rangle =2{\epsilon }^{2/3}{\int }_{0}^{1/{\rm{\Delta }}x}{k}^{2}\,{k}^{-5/3}{dk}\propto {\epsilon }^{2/3}{\rm{\Delta }}{x}^{-4/3},\end{eqnarray} \tag{ 14 }$$

where we have summed the energy spectrum (in k-space) up to the size of the filter scale to capture the subgrid energy. Noting that $\epsilon \propto {v}_{t}^{3}/{\rm{\Delta }}x$ results in

$$\begin{eqnarray}&&{v}_{t}\propto \sqrt{\nu }\ | {\overline{{\rm{}}S}}_{{ij}}| \ {\rm{\Delta }}x,\end{eqnarray} \tag{ 15 }$$

demonstrating that the amplitude of velocity fluctuations on the filter scale is directly related to the magnitude of the rate of strain, as adopted in our simulation and by Smagorinsky: ${v}_{t}=| {\overline{{\rm{}}S}}_{{ij}}| \ {\rm{\Delta }}x$.

Beyond the subgrid model for the pollution of pristine gas described above, we have also modified ramses to include a simple molecular cooling model, which is important for low-temperature cooling in the pristine gas (Johnson & Bromm 2006; Prieto et al. 2008; Hirano & Yoshida 2013). Our model is analytic and based on the work of Martin et al. (1996), which provides a radiative cooling rate per H₂ molecule, ${{\rm{\Lambda }}}_{r}/{n}_{{{\rm{H}}}_{2}}$, across a range of densities, as depicted in Figure 3. We truncate our H₂ cooling model above 50,000 K as the contribution of molecular cooling becomes negligible and molecular hydrogen is highly dissociated above this temperature.

Zoom In Zoom Out Reset image size

The cooling rate is computed for each simulation cell based on the cell's density, temperature, and molecular fraction, ${f}_{{{\rm{H}}}_{2}}$. Our initial ${H}_{2}$ fraction is primordial (${f}_{{{\rm{H}}}_{2}}={10}^{-6};$ Reed et al. 2005); we model the Lyman–Werner flux from our star particles as ${\eta }_{\mathrm{LW}}={10}^{4}$ photons per stellar baryon (Greif & Bromm 2006), and we assume optically thin gas throughout the simulation volume. We compute the number of stellar baryons, ${N}_{* ,b}$, by totaling the mass in star particles, at each simulation step, assuming a near-primordial composition (X = 0.73, Y = 0.25). This results in an updated ${f}_{{{\rm{H}}}_{2}}$ for each simulation step:

$$\begin{eqnarray}&&{f}_{{{\rm{H}}}_{2},{new}}=\displaystyle \frac{({f}_{{{\rm{H}}}_{2},\mathrm{old}}\ {N}_{\mathrm{gas}}-{N}_{\mathrm{LW}})}{{N}_{\mathrm{gas}}},\end{eqnarray} \tag{ 16 }$$

where

$$\begin{eqnarray}&&{N}_{\mathrm{LW}}={N}_{* ,b}\ {\eta }_{\mathrm{LW}}.\end{eqnarray} \tag{ 17 }$$

We note that the total stellar mass created at the onset of star formation generates enough Lyman–Werner flux to permeate our simulation volume of 27 Mpc³ h⁻³ (Johnson et al. 2013; Bromm & Loeb 2003), destroying all of the molecular hydrogen. We do not model subsequent H₂ formation since cooling becomes dominated by metal lines shortly after the first star particles form and any subsequent molecular hydrogen would be quickly destroyed by the Lyman–Werner flux. Hence, our molecular cooling model is significant only for the very first generation of stars.

Metal-line cooling is computed as a function of gas metallicity and temperature using Sutherland & Dopita (1993) for temperatures down to $\approx {10}^{4}\,{\rm{K}}$, below which ramses makes use of Rosen & Bregman (1995). We fix the gas temperature floor at 100 K for radiative cooling although adiabatic cooling below this limit is possible. Lastly, our UV background is based on the work of Haardt & Madau (1996).

Following the cosmic evolution of pristine gas is sensitive to our implementation of star formation and SN generation. ramses creates star particles in regions of gas according to a Schmidt law (Schmidt 1959), as

$$\begin{eqnarray}&&\displaystyle \frac{d{\rho }_{\star }}{{dt}}=\displaystyle \frac{\rho }{{t}_{\star }}\theta (\rho -{\rho }_{\mathrm{th}}),\end{eqnarray} \tag{ 18 }$$

where the Heaviside step function $\theta (\rho -{\rho }_{\mathrm{th}})$ allows for star formation only when the density exceeds a threshold value ${\rho }_{\mathrm{th}}.$ Here we have set ${\rho }_{\mathrm{th}}$ to be the maximum of $0.75\,{m}_{p}\,{\mathrm{cm}}^{-3}$ or 150 times the mean density in the simulation, where the latter criterion ensures that star particles are only formed in virialized halos and not in high-density regions of the cosmological flow (Rasera & Teyssier 2006; Dubois & Teyssier 2008). To generate an SFR in ${M}_{\odot }\,{\mathrm{yr}}^{-1}$ in good agreement with Madau & Dickinson (2014) and Bouwens et al. (2012b), we have tuned the star formation timescale ${t}_{\star }=0.316\,\mathrm{Gyr}$, approximately 5 times the free-fall time, ${t}_{\mathrm{ff}}\equiv {(3\pi /32G\rho )}^{1/2},$ for a gas with $\rho =0.75\,{m}_{p}\,{\mathrm{cm}}^{-3}.$ The mass of the newly created star particle is ${m}_{\star }={\rho }_{\mathrm{th}}{\rm{\Delta }}{x}_{\min }^{3}N$, where ${\rm{\Delta }}{x}_{\min }$ is the best resolution cell size and N is drawn from a Poisson distribution

$$\begin{eqnarray}&&P(N)=\displaystyle \frac{\overline{N}}{N!}\,\exp (-\overline{N}),\end{eqnarray} \tag{ 19 }$$

with

$$\begin{eqnarray}&&\overline{N}=\displaystyle \frac{\rho \,{\rm{\Delta }}{x}^{3}}{{\rho }_{\mathrm{th}}{\rm{\Delta }}{x}_{\min }^{3}}\displaystyle \frac{{\rm{\Delta }}t}{{t}_{\star }}.\end{eqnarray} \tag{ 20 }$$

A further limitation on star particle formulation is that no more than 90% of the cell's gas mass can be converted into stars.

As each star particle represents a mass range of stars, a fraction of the mass will be returned to the grid in the form of SNe. In our simulations, this recycling is assumed to occur after the 10 Myr lifetimes for stars near the top of the IMF (e.g., Raskin et al. 2008). In this case the impact of massive stars is determined by the fraction of the star particle mass they eject, ${\eta }_{\mathrm{SN}},$ and the kinetic energy per unit mass of this ejecta, ${E}_{\mathrm{SN}}$. For simplicity, we take ${\eta }_{\mathrm{SN}}=0.1$ and ${E}_{\mathrm{SN}}=1\times {10}^{51}\,\mathrm{ergs}/10\,{M}_{\odot }$, for all stars formed throughout the simulation, regardless of their primordial fractions. Note, however, that as the Pop III IMF is likely to have been biased to massive stars, metal ejection from such stars may have been more efficient (e.g., Scannapieco et al. 2003; Scannapieco 2005), leading to differences in stellar enrichment, which we plan to explore in future work.

For each newly formed star particle, the ejected mass and energy are deposited into all cells whose centers are within 150 pc, and if the size of the cell containing the particle is greater than 150 pc, the energy and ejecta are deposited into the adjacent cells (Dubois & Teyssier 2008). Here the total mass of the ejecta is that of the stellar material plus an amount of the gas within the cell hosting the star particle (entrained gas) such that ${m}_{\mathrm{ej}}={m}_{\mathrm{sn}}+{m}_{\mathrm{ent}}$, with ${m}_{\mathrm{sn}}\equiv {\eta }_{\mathrm{sn}}\,{m}_{\star }$ and ${m}_{\mathrm{ent}}\equiv \min (10\,{m}_{\mathrm{sn}},\ 0.25\,{\rho }_{\mathrm{cell}}\,{\rm{\Delta }}{x}^{3})$. Similarly, the mass in metals added to the simulation is taken to be 15% of the SN ejecta plus the metals in the entrained material, ${Z}_{\mathrm{ej}}\ {m}_{\mathrm{ej}}={m}_{\mathrm{ent}}\,Z+0.15\,{m}_{\mathrm{sn}},$ and the mass in primordial metals is taken to be ${Z}_{{\rm{P}},\mathrm{ej}}\ {m}_{\mathrm{ej}}={m}_{\mathrm{ent}}\,{Z}_{{\rm{P}}}+0.15\,{m}_{\mathrm{sn}}\,{P}_{\star }.$ SN energy is the dominate driver of turbulence in our simulation, and we have chosen to partition it equally between kinetic and thermal energy. We do not model black hole formation or feedback.

Since our SN feedback model deposits SN energy in the surrounding cells, it tends to leave the central portion of the star-forming cloud, in the host cell, mostly intact. Additionally, while radiative feedback, especially from massive stars, can be quite effective in evacuating gas and disrupting star formation in small halos (Wise et al. 2012; Whalen et al. 2004), we have not modeled it in this simulation. Conversely, however, the ionization and shock fronts created by radiative feedback may also trigger star formation in clumps or pillars (Deharveng et al. 2010; Tremblin et al. 2012) of very dense gas that are likely to form near the shock boundary. Given these considerations, we feel that our approach is a reasonable starting point for modeling star formation in turbulent flows. We leave the analysis of the impact of radiative feedback and different SN energies for future study.

We evolved a cubic 3 Mpc h⁻¹ comoving box from z = 499 to z = 5 starting from initial conditions generated by the mpgrafic code (Prunet et al. 2008). The initial gas metallicity was $Z={Z}_{{\rm{P}}}=0,$ the initial H₂ fraction was ${10}^{-6},$ and we define ${Z}_{\mathrm{crit}}={10}^{-5}\,{Z}_{\odot }.$ The base resolution was 512³ cells (${l}_{\min }=9$), corresponding to a grid resolution of 5.86 comoving kpc h⁻¹ and a dark matter particle mass of $5.58\times {10}^{4}\,{h}^{-1}\,{{\rm{\Omega }}}_{{\rm{DM}}}\,{M}_{\odot }.$ We refined cells as they become $8\times$ overdense, or when the local Jeans length is less than four times the current cell size, ensuring that we always resolved the Jeans length with at least four simulation cells. We allowed for up to eight additional refinement levels (${l}_{\max }=17$), using a Courant factor of 0.8, resulting in a best possible spatial resolution of 23 physical pc h⁻¹. However, because these additional levels maintain a maximum physical resolution rather than a comoving resolution, the highest resolution reached by z = 5 was level 14. Our settings resulted in a range of star particle masses between $726\,{M}_{\odot }\leqslant M\leqslant 3628\,{M}_{\odot }$. The nonlinear length scale at the end of the simulation was 0.15 h⁻¹ comoving Mpc, corresponding to a mass of $1.5\times {10}^{9}\,{M}_{\odot }.$ Finally, we tuned the code reionization parameters to ensure that the reionization redshift agrees with recent results (specifically, ${z}_{\mathrm{reion}}\approx 8.8;$ Planck Collaboration et al. 2015).

Our simulation generated a total of 345 halos (at z = 5) with a mass range of 79,000 to 372,468,025 M_⊙. The largest halo was composed of 513,749 star particles, while the smallest considered had 109. Halos needed to consist of at least 100 star particles before we counted them in this total. Our star formation overdensity threshold ($150\times$ overdense) ensured that star formation only occurred in and around collapsed objects. The mean matter density of our simulation in terms of the average matter density of the universe was $\langle {\rho }_{\mathrm{sim}}\rangle /({\rho }_{\mathrm{crit}}{{\rm{\Omega }}}_{{\rm{M}}})=1.001$, indicating that our volume represents a typical region of the universe.

Figure 4 shows the evolution of the SFR density in our simulation, along with observational results compiled by Madau & Dickinson (2014) from Bouwens et al. (2012a, 2012b). The onset of star formation occurs at $z\approx 18,$ which quickly dissociates the small initial level of H₂ in the box, raising the minimum virial temperature of halos in which stars can form efficiently to $\approx {10}^{4}\,{\rm{K}}$. This is above the nonlinear scale for redshifts above $z\approx 6,$ and so the SFR density increases roughly exponentially with decreasing redshift throughout the simulation, with some flattening below the redshift of reionization (Scannapieco 2005). This overall rate is also in good agreement with $z\leqslant 7$ observations, and while our results are somewhat higher than observations at z = 8, this is to be expected as galaxy surveys are magnitude limited, while our simulations also include star formation down to very small mass limits.

Zoom In Zoom Out Reset image size

For comparison, our high-redshift SFR density is much lower than the one obtained from the Renaissance zoom simulation of a "normal" region of the universe (Xu et al. 2016). However, their simulation retains a maximum resolution of 19 comoving pc, while ours maintains a maximum resolution of 23 physical pc. At their final simulation redshift of $z\approx 12.5$, this corresponds to a physical resolution of ≈1.5 pc versus our ≈23 pc, allowing them to trace star formation in much smaller objects than we track and discuss here.

While the very first stars in our simulation are purely metal-free (Pop III), they quickly generate SNe, and the resulting pollution of the pristine gas gives rise to subsequent stellar populations with varying levels of metals. As our subgrid models allow us to track the pristine gas fraction for every particle, we can calculate not only the "classically determined" Pop III SFR in $\overline{Z}\lt {Z}_{\mathrm{crit}}$ regions but also the formation of stars in unmixed regions with $\overline{Z}\gt {Z}_{\mathrm{crit}}$ as ${P}_{\star }\times {m}_{\star }$. In the classically determined case, our results are in good agreement with the simulations of Pallottini et al. (2014; see also Tornatore et al. 2007) over the range $5\leqslant z\leqslant 8,$ while at higher redshifts our rate is somewhat higher, most likely due to our higher base resolution (5.86 versus 19.53 comoving kpc h⁻¹). This extended evolution is indicative of a large-scale spatially inhomogeneous Pop III/Pop II transition as progressively lower-sigma peaks collapse and form stars in regions far away from sites of previous metal enrichment (Scannapieco et al. 2003).

On the other hand, including metal-free star formation in unmixed regions with $\overline{Z}\gt {Z}_{\mathrm{crit}}$ leads to an increase in the Pop III rate by a factor of 2–3 over the full range from $5\leqslant z\leqslant 16.$ This indicates that small-scale mixing is at least as important as large-scale inhomogeneities in determining the history of metal-free star formation. Or, in other words, at least as many Pop III stars are formed within metal-enriched protogalaxies as are formed in purely metal-free objects.

As noted earlier, our SFR density is dependent on the stellar and SN feedback prescriptions we have adopted, which are the standard ones in ramses. In particular, we have not modeled radiative feedback from these first, massive stars. As discussed in Whalen et al. (2004), such feedback is likely quite effective in dispersing the original star-forming cloud. We leave the modeling of radiative feedback—as well as progenitor-dependent SN energy—to a follow-up work.

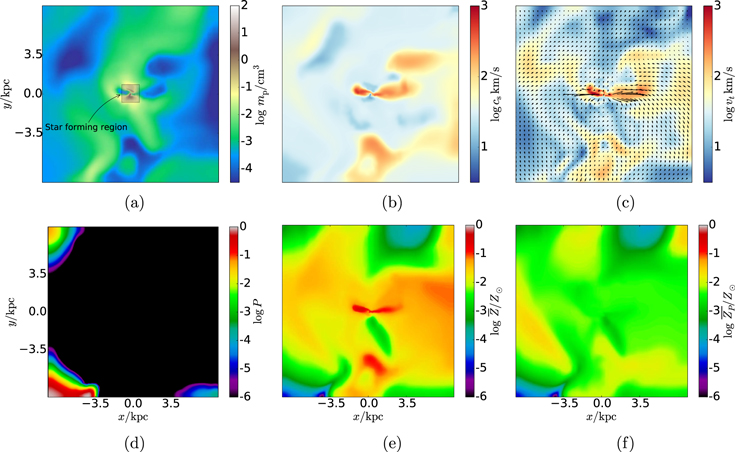
To better understand this small-scale pollution of metals, we examine two representative star-forming regions in detail. In Figure 5, we show the characteristics of the gas at $z=16,$ in one of the earliest star-forming regions in our simulation. In the center of panel (a) in this figure, we see the overdense region of gas in which star formation and a burst of SNe have recently occurred. In fact, this is the first occurrence of SNe in this halo. We again point out that each SN in our simulation represents the combined action of $\approx 4\mbox{--}20$ SNe, due to our star particle mass range. Panels (b) and (c) depict the impact of the SN burst in terms of the sound speed of the gas (which is $0.15\,\mathrm{km}\,{{\rm{s}}}^{-1}\,{({\rm{T}}/{\rm{K}})}^{1/2}$) and the turbulent velocity. Here we see how SNe heat the surrounding gas to sound speeds of $\gtrsim 200$ km s⁻¹, corresponding to ${10}^{6}\mbox{--}{10}^{7}$ K. These temperatures, while high, are much lower than the initial temperatures at the time at which the SNe occurred in the simulation, because the gas is strongly cooled by adiabatic expansion as the high-pressure regions expand into the intergalactic medium. Thus, the radial velocities in panel (c) (vector overlay) are over 300 km s⁻¹, resulting in shear strong enough to generate turbulent velocities up to $\approx 500$ km s⁻¹. This typically leads to supersonic subgrid turbulent mixing, as discussed in Section 2.2.2. The value of the pristine fraction shortly after a burst of SN occurs is set by the mass density of ejecta relative to the newly polluted cells' mass densities, as described in Section 2.1. Further, while we have demonstrated that the ISM is likely highly turbulent for reasons previously described, we note that in the case of a compressive shock, the subgrid mixing time is proportional to the sound-crossing time in the cell: ${\rm{\Delta }}x/{c}_{s}$. This is just another way of saying that the mixing time is proportional to the time it takes the shocked gas, along with the pollutants, to cross the cell. As can be seen in Figure 5, in a mostly radially expanding shock, apparently dominated by compressive modes, our formulation appropriately models the mixing time, $\tau \propto {v}_{t}^{-1}$, since in the radial case ${v}_{t}\propto {v}_{r}$, where v_r is the radial velocity of the shocked gas. This situation only arises in areas of pristine, low-density gas that has not been previously stirred by SN or other dynamical effects (e.g., gravitational shear). However, we say "apparently" here since even a single SN shock expanding into a uniform medium is likely far from purely compressive owing to instabilities in the blast that start within the SN. Such instabilities generate vorticity, resulting in clumpy, turbulent ejecta (Padoan et al. 2007).

Zoom In Zoom Out Reset image size

In the lower panels of this figure, we see two regions of gas with $\overline{Z}\approx {10}^{-1}\,{Z}_{\odot }$ (red areas in panel (e)). These areas also have the highest polluted fractions ($P\lesssim 1 \%$, or ${f}_{\mathrm{pol}}\gtrsim 0.99$), as depicted in panel (d). These areas are found close to the sites of the SNe, in low-density gas, and thus they have been turbulently stirred for the longest times. In addition, the turbulent velocity and sound speed are comparable in these regions, implying subsonic turbulent mixing, which operates more efficiently than supersonic mixing, as discussed above. We also see a very small region of highly pristine gas in the area of high-density gas near the center of the halo. This pocket of gas, with $\overline{Z}\approx {10}^{-3}$, if it were to collapse, is capable of producing star particles with a very high pristine fraction.

Moving farther out from the center, we see that the average metallicity of the gas falls off relatively slowly, indicating that polluted material has been carried most of the way across this region. However, the radial increase in the pristine fraction is much steeper, moving to $\gtrsim 10 \%$ in $\overline{Z}\lesssim {10}^{-2.5}\,{Z}_{\odot }$ areas and increasing to $\approx 100 \%$ in areas where $\overline{Z}\lesssim {10}^{-4}\,{Z}_{\odot }$. This unmixed gas occurs in the regions in which the turbulent velocity drops sharply, illustrating the correlation between turbulent mixing, the kinetic energy, and the sound speed in the gas. Finally, we note that the vast majority of metals are from primordial stars, indicated by the nearly identical plots for ${\overline{Z}}_{{\rm{P}}}$ and $\overline{Z}$.

Figure 6 depicts the gas in a $100\,\mathrm{kpc}\,{h}^{-1}$ comoving star-forming region at z = 8. Unlike in the early halo case shown in Figure 5, most of the gas in this case is thoroughly mixed. The metallicity plot shows that the gas has been enriched to at least $\overline{Z}\geqslant {10}^{-3}\,{Z}_{\odot }$ throughout most of this slice. Looking at the sound speed and turbulent velocity plots, we note that, in general, there are few regions where ${v}_{{\rm{t}}}\gg {c}_{{\rm{s}}}$, indicating that SN energy has mostly been disbursed—another indication that there has been sufficient time for mixing to occur. On the other hand, there remain pockets of gas around the edge of this slice in which the overall metallicity is relatively high, $\overline{Z}\gtrsim {10}^{-3}\,{Z}_{\odot }$, but where $P\gtrsim {10}^{-2}$. These regions of incomplete mixing correlated with regions of lower density. By comparing $\overline{Z}$ to ${\overline{Z}}_{P}$, we note that, roughly, only 10% of the metals in this region are primordial, indicating thorough pollution by a second generation of SNe. Interestingly however, there is one region just below the central star-forming region with $\overline{Z}\approx {10}^{-3}\,{Z}_{\odot }$ with densities of ${10}^{-1}\,{m}_{{\rm{p}}}\,{\mathrm{cm}}^{-3}\lt \rho \leqslant {10}^{-2.5}\,{m}_{{\rm{p}}}\,{\mathrm{cm}}^{-3}$ where we find $\overline{Z}\approx {\overline{Z}}_{P},$ indicating that most of the metals here are likely from first-generation ejecta. Should subsequent star formation occur in this moderately dense region, we would expect a population of stars with a high fraction of primordial metals. Even in this seemingly well polluted region our two new scalars have allowed us to paint a more nuanced picture of metal enrichment of the gas, which will lead to important observable differences for the resulting stellar populations.

Zoom In Zoom Out Reset image size

Figure 7 shows several properties of stars formed in a representative minihalo at z = 16. Note that the metallicities in this figure are corrected to correspond to the metallicities of the subset of enriched stars within the star particle, ${Z}_{\star }={\overline{Z}}_{\star }{f}_{\mathrm{pol}}^{-1}$, as described in Section 2. Here we have used the upper bound for the correction to the metallicity since we are at high redshift and the gas in and around the halos is in the process of being enriched by a group of SNe. As the star particles in the top left plot of panel (a) in this figure have ${Z}_{\star }\leqslant {Z}_{\mathrm{crit}},$ even after correcting for ${f}_{\mathrm{pol}}$, they represent stellar mass composed of pristine material, labeled as "classical" Pop III stars in Figure 4. Such particles make up about 17% of the stellar mass of this early halo, as compared to the majority of the star particles thta fall into the metallicity bin ${10}^{-3}\,{Z}_{\odot }\lt {Z}_{\star }\leqslant {10}^{-1}\,{Z}_{\odot }.$ Interestingly, correcting for the polluted fraction of gas results in no stars in the metallicity bin ${10}^{-5}\,{Z}_{\odot }\lt {Z}_{\star }\leqslant {10}^{-3}\,{Z}_{\odot }.$ This indicates that the polluted fraction of the cell must have been relatively small when ejecta in this range polluted star-forming cells, resulting in enhanced metallicities (${Z}_{\star }\gt {10}^{-3}\,{Z}_{\odot }$) due to the concentration of the metals. This can be easily seen in the top panels of Figure 8. Examining the pristine and polluted fraction plots, it is apparent that many of the higher-Z_⋆ star particles reach these high corrected metallicities only because they have not only pristine fractions P_⋆ greater than 10% but also polluted fractions ${f}_{\mathrm{pol}}=1-{P}_{\star }$ less than 10%, implying ${P}_{\star }\gt 0.9;$ this means that the majority of the gas from which they were formed was unmixed. In fact, if we include the pristine fractions of all star particles, the Pop III fraction for this halo grows to 57%, an increase of a factor of nearly 3.4. However, we note several star particles in panel (a), ${10}^{-3}\,{Z}_{\odot }\lt {Z}_{\star }\leqslant {10}^{-1}\,{Z}_{\odot }$, to the lower right of the central concentration of particles, that do not appear in the pristine fraction plot for ${P}_{\star }\gt {10}^{-1}$. These star particles formed at a later time in gas that was more thoroughly mixed and represent a relatively small population of almost all Pop II stars with ${10}^{-5}\lt {P}_{\star }\leqslant {10}^{-3}$. Additionally, by comparing the spatial distribution of stars as a function of metallicity, ${Z}_{\star },$ to the distribution of stars as a function of primordial metallicity, ${Z}_{{\rm{P}},\star },$ we can see that almost all of the metals in the enriched stars within this halo are produced by Pop III stars.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

These conclusions are supported by Figure 8, which shows the total, Pop III, and primordial stellar masses (${f}_{\mathrm{pol}}\times {M}_{\star }\times \tfrac{{Z}_{P\star }}{{Z}_{\star }}$) binned according to the star particles' corrected metallicity (right side). For comparison, we also include an uncorrected metallicity histogram to show the effects of the ${f}_{\mathrm{pol}}$ correction to ${\overline{Z}}_{\star }$. While there are a fair number of star particles with average metallicities in the range ${10}^{-5}\,{Z}_{\odot }\lt {\overline{Z}}_{\star }\lesssim {10}^{-2.6}\,{Z}_{\odot },$ the lowest nonzero corrected metallicities are $\approx {10}^{-3.1}\,{Z}_{\odot }.$ In fact, after correcting for the polluted fraction, these extremely low average metallicity star particles are among the star particles with the highest corrected metallicities, such that star particles with ${Z}_{\star }\gtrsim {10}^{-1.6}\,{Z}_{\odot }$ are over 99.6% pristine. These are the star particles that form at the edges of the extent of enriched material, still within the central star-forming region, in which the average gas metallicity is low but very little mixing has occurred, such that the metals are concentrated into just a few stars.

As mentioned above, we have not modeled radiative feedback in our simulation, and our example halo at z = 16 formed classical Pop III stars in two successive yet closely spaced (${\rm{\Delta }}t\lt 7$ Myr) waves. Even though radiative feedback from these stars would likely lower densities and suppress further central star formation (Wise et al. 2012), it is also possible for feedback to trigger nearby collapse in dense clumps in the pristine gas. Our simulation indicates that subsequent significant star formation in this halo takes place on a timescale of $\lt 20\,\mathrm{Myr}$, such that star particles still have relatively high pristine fraction, $P\gt 0.1$. While we feel that these results are representative, it will be interesting to model radiative feedback and quantify the differences.

Moving to ${10}^{-2.8}\,{Z}_{\odot }\lt {Z}_{\star }\lesssim {10}^{-1.6}\,{Z}_{\odot }$ star particles formed in more vigorously stirred material, we find that 38% of this material is composed of Pop III stars. In fact, only when one also includes star particles with average metallicities up to ${10}^{-1.6}\,{Z}_{\odot }$ does one arrive at a 57% mass fraction of Pop III stars in this object. Finally, from the primordial stellar mass histograms we can see that the majority of enriched stars are found in ${10}^{-2.5}\,{Z}_{\odot }\lt {\overline{Z}}_{\star }\lesssim {10}^{-1.5}\,{Z}_{\odot }$ particles, and that in these particles, essentially all the metals are generated by Pop III stars.

In Figure 9, we turn our attention to the properties of the stars formed in a halo at z = 8. Unlike Figure 7, which shows a different z = 16 region than shown in the gas plots in Figure 5, Figure 9 shows the stellar distribution in the same region at the center of the z = 8 region depicted in Figure 6. This halo is older than the z = 16 halo and has formed stars over a longer period, resulting in more metals and significantly more mixing. However, while the more extended history shifts the average metallicity to somewhat higher values than in the z = 16 case, they still share many features. In both halos, the largest collection of star particles occurs in the ${10}^{-3}\,{Z}_{\odot }\lt {Z}_{\star }\leqslant {10}^{-1}\,{Z}_{\odot }$ range, in both halos there are a large number of star particles with ${f}_{\mathrm{pol}}\lt 0.1$, and in both halos a significant number of Pop III stars are formed.

Zoom In Zoom Out Reset image size

On the other hand, unlike the higher-redshift case, second-generation metals are present in the z = 8 halo, as can be seen by comparing the total metallicity in panel (a) to the primordial metallicity in panel (b). This shows that the primordial metals are down by a factor of $\approx 3$ from the Z_⋆ levels. And while there is a large fraction of star particles with ${P}_{\star }\gt 0.1$, there is also now a comparable fraction with ${P}_{\star }\leqslant {10}^{-5}$, indicating a large fraction of star particles fully polluted with metals.

Figure 10 depicts the metallicity distribution for the star particles in this minihalo. As visible in the scatter plots, a much larger fraction of stars in the range ${10}^{-1.8}\,{Z}_{\odot }\lt {Z}_{\star }\lesssim {10}^{-1.1}\,{Z}_{\odot }$ are polluted (95%), and the fraction of primordial metals, 0.13, is much lower than in the earlier halo. However, looking at stars in the range ${10}^{-2.7}\,{Z}_{\odot }\lt {Z}_{\star }\leqslant {10}^{-1.8}\,{Z}_{\odot }$, we again see a population of Pop II stars with a high fraction of primordial metals. These most likely represent an older population that was mostly polluted with Pop III material, which are likely good CEMP candidates. We also note another large Pop III group of stars born in largely unmixed gas with $Z\geqslant {10}^{-1.1}\,{Z}_{\odot }$. In fact, 99% of the stars in these star particles are pristine. For comparison, Table 2 captures some of the relevant characteristics of the two halos we have been discussing. Here, angle brackets around the metallicity indicate a mass-weighted average taken over all stars in the halo.

Zoom In Zoom Out Reset image size

Table 2.  Halo Characteristics

	Total	Pop III	$\underline{\mathrm{Classic}\ \ \mathrm{Pop}\ \mathrm{III}}$
Redshift	$M/{M}_{\odot }$	$M/{M}_{\odot }$	Pop III	$\langle {Z}_{\star }\rangle$ a	$\langle {Z}_{{\rm{P}},\star }/{Z}_{\star }\rangle$ b
16	$5.35\times {10}^{5}$	$3.04\times {10}^{5}$	0.300	$3.07\times {10}^{-3}$	0.988
8	$1.45\times {10}^{6}$	$6.19\times {10}^{5}$	0.714	$1.53\times {10}^{-2}$	0.322

Notes.

^aMass-weighted average metallicity for all stars in the halo. ^bMass-weighted average primordial metal fraction for polluted stars in the halo.

Download table as:  ASCIITypeset image

Finally, we examine the evolution of the metallicity of our star particles in aggregate. Figure 11 depicts the evolution of the mass-weighted PDF for our star particles, with the primordial metal fraction, ${Z}_{{\rm{P}},\star }/{Z}_{\star }$, plotted against the corrected metallicity, Z_⋆. As expected, as metallicity increases, the fraction of primordial metals decreases (at every epoch), giving the plots their characteristic negative slope. By redshift 5, the majority of the stars have metallicities in the range ${10}^{-1.8}\,{Z}_{\odot }\lt {Z}_{\star }\lt {10}^{-0.5}\,{Z}_{\odot }$. As we move to extremely metal-poor populations, ${Z}_{\star }\lt {10}^{-3}$, the negative slope of our PDF indicates that the fraction of primordial metals increases as overall metallicity decreases such that most of the stars have ${Z}_{{\rm{P}}}/{Z}_{\star }\gt {10}^{-1}$. These Population II stars are likely CEMP candidates. Furthermore, the distribution of stars with ${Z}_{\star }\lt {10}^{-1.5}\,{Z}_{\odot }$ remains roughly constant below $z=6$, indicating that most of the low-metallicity stars, including those with a high fraction of primordial metals, have been formed before this epoch.

Zoom In Zoom Out Reset image size

As in previous diagrams, we have used the upper bound for the corrected metallicity to make these plots. For comparison, the lower left panel, annotated "Uncorrected," shows the effects of not making the polluted fraction correction to the metallicity at z = 5. The ${f}_{\mathrm{pol}}$ correction is greatest for star particles with ${\overline{Z}}_{\star }\lesssim {10}^{-3.5}$ since these were contaminated by material with both a low average metallicity and a small ${f}_{\mathrm{pol}}$. Without this correction, we would predict a larger number of stars with metallicities near ${Z}_{\mathrm{crit}},$ while the corrected results show very few stars enhanced to values below ${10}^{-4}\,{Z}_{\odot }.$ The correction also shifts the population of purely primordial star particles, ${Z}_{{\rm{P}}}/{Z}_{\star }=1$ at z = 5, away from very low metallicities, concentrating them in the range ${10}^{-3}\,{Z}_{\odot }\lt {Z}_{\star }\lt {10}^{-1}\,{Z}_{\odot }$. While stars in this metallicity range are not extremely metal-poor, they do possess a large fraction of primordial metals and may represent an important iron-poor stellar population.

For comparison, we include PDF plots for the lower bound on the correction to Z_⋆. As can be seen in Figure 12, if we assume that the maximum amount of metals in these star particles is distributed in the Pop III stars, at a level ${Z}_{\star }\lesssim {Z}_{\mathrm{crit}}$, we reduce the enhancement of the lowest-metallicity stars. This is clearly depicted in the lower left panel, where we have differenced the masses in the metallicity bins between the upper and lower bounds for star particles at z = 5.0.

Zoom In Zoom Out Reset image size

The two types of metallicity associated with our star particles, Z_⋆ and ${Z}_{{\rm{P}},\star }$, provide us with the information needed to more accurately model their chemical makeup and compare them with observations. Motivated by the lack of $Z\leqslant {10}^{-1.5}\,{Z}_{\odot }$ Pop II star formation below $z=6,$ we assume that at ${10}^{-1.5}\,{Z}_{\odot }$ the final distribution of enriched stars in our simulation can be compared with the distribution of metal-poor halo stars, and we model the abundances of our stars as the convolution of the ejecta of a single type of Pop III SNe (for ${Z}_{{\rm{P}},\star }$) and a single set of abundances representative of second-generation metals (for Z_⋆) at z = 5. While a more heterogeneous model for Pop III SN ejecta would be more physical (Heger & Woosley 2002; Ishigaki et al. 2014), it would also introduce additional parameters into the problem, and thus we focus in this first paper on a single representative model for this study. Specifically, we model the metallicity produced by primordial stars as the yield from $60\,{M}_{\odot }$ Pop III SNe (Heger 2016). This very iron-poor and carbon-enhanced ejecta is a best fit for the CEMP star SMSS J031300.36-670839.3, studied by Keller et al. (2014), and is representative of core-collapse SN yields in the $25\,{M}_{\odot }\leqslant {M}_{\star }\leqslant 140\,{M}_{\odot }$ range in which metal yields are believed to be carbon-enhanced and iron-poor (Heger & Woosley 2002). The composition typical of z = 5 was determined by a chemical evolution model run to that epoch by F. X. Timmes (2016, private communication). We capture the characteristics of these two types of material in Table 3.

Table 3.  Mass Fractions of Metals

	$X/Z$	$X/{Z}_{P}$
Element	1 Gyr	$60\,{M}_{\odot }$ Pop III SNe
C	1.68 × 10−1	7.11 × 10−1
O	5.29 × 10−1	2.73 × 10−1
Mg	2.49 × 10−2	9.56 × 10−4
Ca	3.00 × 10−3	1.43 × 10−7
Fe	5.39 × 10−2	2.64 × 10−12

Note. The mass fractions of metals for selected elements used to model the normal and primordial metallicity of star particles in our simulation. Data for gas typical of 1 Gyr after the big bang are provided by F. X. Timmes (2016, private communication). Data for $60\,{M}_{\odot }$ Pop III SNe are provided by Heger (2016).

Download table as:  ASCIITypeset image

Before continuing, we note that we also explored different progenitor yields when attempting to match the metal abundances observed in Keller et al. (2014). The yield for a $25\,{M}_{\odot }$ Pop III SN (Umeda & Nomoto 2003) was the next most promising progenitor candidate; however, it did not correctly reproduce the abundances of [Mg/Ca] observed.

Using the $60\,{M}_{\odot }$ Pop III SN yields, we model ratios of [C/H], [O/H], and [Mg/Ca] to [Fe/H] for stars in our simulation as

$$\begin{eqnarray}&&{Z}_{\star }^{i}=({Z}_{\star }-{Z}_{{\rm{P}},\star }){X}_{{\rm{T}}}^{i}+{Z}_{{\rm{P}},\star }\,{X}_{60\mathrm{SN}}^{i}.\end{eqnarray} \tag{ 21 }$$

Here, ${Z}_{\star }^{i}$ denotes the star particle's final mass fraction (not solar units) of $i\,\in$ [C, O, Mg, Ca, Fe], and the subscripts T and 60 SN denote the mass fractions of these elements in F. X. Timmes (2016, private communication) and Heger (2016), respectively. The results are displayed in Figure 13, in which we present mass-weighted, joint PDFs for all of the stars in our simulation. The probabilities have been determined using each star particle's corrected metallicity and primordial metallicity as described above. Once again, we have used the upper bound for the correction to star particle metallicity. Using the lower bound does not change the probability distribution and hence does not make a difference in this analysis. The PDFs have also been normalized by the logarithmic bin size and the comoving simulation volume. As the F. X. Timmes (2016, private communication) iron yields are [Fe/H] ≈ −0.5, and very few $Z\lt {10}^{-1.5}\,{Z}_{\odot }$ Pop II stars are formed below $z=6,$ as shown in Figure 11, we focus on the [Fe/H] range below −2, for which the z = 5 results can be related to stars observed today. In this range, for comparison, we have overplotted the CEMP stars from Keller et al. (2014), with uncertainties, where known.

Zoom In Zoom Out Reset image size

Without any fine-tuning, our model results in reasonable agreement between the simulation's results and the observed characteristics of metal-poor stars, albeit using a single progenitor yield model. Note that this is not guaranteed by our choice of Pop III yields, which were selected by Keller et al. (2014) to reproduce the properties of a single extremely metal-poor star, but are now being convolved with a wide range of Z_⋆ and ${Z}_{{\rm{P}},\star }$ values. Nevertheless, our model captures many of the features observed in the data. While [Fe/H] can reach extremely low values due to the lack of iron in our Pop III yields, [C/H] and [O/H] are always greater than −4 and almost always greater than −3. Note that the lack of such extremely carbon- and oxygen-poor stars would not be reproduced in models that did not apply corrections to boost the observed metallicities of low-${\overline{Z}}_{\star }$ star particles with small polluted fractions. Furthermore, our simulations reproduce many other features suggested by the data, including the enhanced probability of finding CEMP stars with [C/H] ≈ −1.5 or with [C/Fe] ≈ 0.5, the enhanced probability of finding low-[Fe/H] stars with [O/H] ≈ −2, and the preponderance of low-[Fe/H] stars with [Mg/Ca] ≈ 0.

The histogram at the lower left of this figure depicts the mass-weighted metallicity density function (MDF) for our model overlaid with MDFs derived from MW halo populations (An et al. 2013; Yoon et al. 2016). To account for the fact that these have been derived from surveys targeted to find stars in a specific metallicity range, each of the observational MDFs has been normalized to the simulation's average MDF value over their respective intervals. Additionally, we have included 1σ Poisson noise based on the original data for each set of observations.

Given the very low number of stars observed below [Fe/H] = −4.5, and since these MDFs were derived from local observational data over specific, and limited, metallicity ranges, we do not expect a tight correlation with our global MDF at z = 5. Specifically, the MDF for −4.3 ≤ [Fe/H] ≤ −2.8 exhibits selection effects based on the authors' focus on CEMP stars, not all metal-poor stars (Yoon et al. 2016), and consists of high-resolution observations selected from medium-resolution spectra likely to be extremely metal-poor. On the other hand, the An et al. (2013) higher-metallicity MDF, [Fe/H] > −3.8, is focused on medium-resolution spectroscopy that makes it hard to identify stars at the low end of the metallicity range, so we have chosen to use [Fe/H] ≥ −2.8 for these data.