TURBULENT MIXING ON HELIUM-ACCRETING WHITE DWARFS

Material accreting onto a WD at a rate $\dot{M}$ reaches its surface with a nearly Keplerian spin frequency

$$\begin{eqnarray}&&{{{\Omega }}_{K}}={{(GM/{{R}^{3}})}^{1/2}}=1.0M_{1}^{1/2}R_{8.7}^{-3/2}\;{{{\rm s}}^{-1}},\end{eqnarray} \tag{ 1 }$$

where ${{M}_{1}}=M/1\;{{M}_{\odot }}$ and ${{R}_{8.7}}=R/5\times {{10}^{8}}\;{\rm cm}$ are the typical WD mass and radius I will be considering. Most of the energy of this incoming material is dissipated in a thin boundary layer and does not reach far into the star (Piro & Bildsten 2004). Nevertheless, this material adds angular momentum at a rate of ${{(GMR)}^{1/2}}\dot{M}$, and so a torque of this magnitude must be present to transport the angular momentum through the WD and increase its spin.

Since these shallow surface layers of the WD have a typical pressure scale height $H\ll R$, where $H=P/\rho g$ and $g=GM/{{R}^{2}}$ is the surface gravitational acceleration, I assume a plane-parallel geometry and set R as the radius and use z as the vertical height coordinate above R. This also allows me to introduce a useful variable in the column depth

$$\begin{eqnarray}&&d{\Sigma }=-\rho dz,\end{eqnarray} \tag{ 2 }$$

to measure the depth in the atmosphere. In the plane-parallel limit, the pressure given by hydrostatic equilibrium is simply $P={\Sigma }g$. In this geometry, the transport of angular momentum is described by a one-dimensional diffusion equation (Fujimoto 1993)

$$\begin{eqnarray}&&\frac{d}{dt}\left( {{R}^{2}}{\Omega } \right)=\frac{1}{{{R}^{2}}\rho }\frac{\partial }{\partial z}\left( \rho \nu {{R}^{4}}\frac{\partial {\Omega }}{\partial z} \right),\end{eqnarray} \tag{ 3 }$$

where Ω is the spin of the WD and ν is the viscosity for transporting angular momentum. In principle ν could be something like a molecular diffusivity, but this is never relevant for the cases considered here and I instead focus on ν as a turbulent diffusivity.

Equation (3) can be significantly simplified by assuming steady-state transport of angular momentum (also see Piro 2008). This is reasonable as long as the angular momentum diffusion timescale at a given depth

$$\begin{eqnarray}&&{{t}_{{\rm visc}}}={{H}^{2}}/\nu ,\end{eqnarray} \tag{ 4 }$$

is less than the timescale to accrete down to that same depth

$$\begin{eqnarray}&&{{t}_{{\rm acc}}}=4\pi {{R}^{2}}{\Sigma }/\dot{M},\end{eqnarray} \tag{ 5 }$$

which is easily satisfied in the WD surface layers. The total time derivative then simplifies to $d/dt\approx {{V}_{{\rm adv}}}\partial /\partial z$, where ${{V}_{{\rm adv}}}=-\dot{M}/4\pi {{R}^{2}}\rho$ is the advecting velocity of the fluid in an Eulerian frame. Making this substitution, integrating with respect to z, and taking the limit ${\Omega }\ll {{{\Omega }}_{K}}$, the final result is

$$\begin{eqnarray}&&\sigma =\frac{\dot{M}{{{\Omega }}_{K}}}{4\pi R\rho \nu },\end{eqnarray} \tag{ 6 }$$

where $\sigma =d{\Omega }/d{\rm ln} r$ is the shear rate in the WD. Note that this can also be rewritten in the dimensionless form

$$\begin{eqnarray}&&\frac{\sigma }{{\Omega }}=\left( \frac{{{t}_{{\rm visc}}}}{{{t}_{{\rm acc}}}} \right)\left( \frac{R}{H} \right)\left( \frac{{{{\Omega }}_{K}}}{{\Omega }} \right).\end{eqnarray} \tag{ 7 }$$

This shows that a non-zero shear must exist throughout the star to allow the star to spin up and that it is larger when the viscosity is small (so that ${{t}_{{\rm visc}}}$ is big), the accretion rate is large (so that ${{t}_{{\rm acc}}}$ is small), the thickness H of the layer is smaller, or when the spin Ω is smaller.

Traditionally mixing is modeled as a diffusive process where for some element i with mass fraction X_i,

$$\begin{eqnarray}&&\frac{d{{X}_{i}}}{dt}=\frac{1}{{{r}^{2}}\rho }\frac{\partial }{\partial r}\left( {{r}^{2}}\rho D\frac{\partial {{X}_{i}}}{\partial r} \right),\end{eqnarray} \tag{ 8 }$$

where ρ is the density and D is the diffusion coefficient for mixing, which will vary with depth in the star. While this is well-suited for implementation in one-dimensional stellar evolution codes (e.g., Heger et al. 2000), an alternative way to think about the mixing is like convection. Just as a region in the star is either convectively mixed or not, a region in the star can be turbulently mixed or not.

The general picture I employ is summarized in Figure 1 and described next. After accreting at a rate $\dot{M}$ for a timescale ${{t}_{{\rm acc}}}$, the column depth at the base of the accretion is

$$\begin{eqnarray}&&{{{\Sigma }}_{{\rm acc}}}=\frac{\dot{M}{{t}_{{\rm acc}}}}{4\pi {{R}^{2}}},\end{eqnarray} \tag{ 9 }$$

as shown by the horizontal dashed line in Figure 1. The turbulent mixing time at this depth is estimated as

$$\begin{eqnarray}&&{{t}_{{\rm mix}}}({{{\Sigma }}_{{\rm acc}}})={{H}^{2}}/D,\end{eqnarray} \tag{ 10 }$$

where the right-hand side is evaluated at ${{{\Sigma }}_{{\rm acc}}}$. If ${{t}_{{\rm mix}}}({{{\Sigma }}_{{\rm acc}}})\gt {{t}_{{\rm acc}}}$, then the mixing takes too long to act in comparison to the accretion and there is minimal mixing. If instead ${{t}_{{\rm mix}}}({{{\Sigma }}_{{\rm acc}}})\lt {{t}_{{\rm acc}}}$, then the mixing can carry material to depths larger than the accretion depth.

Zoom In Zoom Out Reset image size

Evaluating ${{t}_{{\rm mix}}}$ at every depth in the star, one can then find the depth where ${{t}_{{\rm mix}}}={{t}_{{\rm acc}}}$, which is denoted ${{{\Sigma }}_{{\rm mix}}}$. This is the depth down to where material is mixed, as shown in light gray in Figure 1. I assume everything is uniformly mixed down to this depth, which is roughly correct because the mixing timescale ${{t}_{{\rm mix}}}$ is generally smaller at shallower depths. Thus if something mixes just a little at the base of the mixed region, the mixing is fast enough to mix it everywhere above this depth. In a sense, this is analogous to the widely used assumption of complete mixing in the convective regions of stars. Since material is mixed down to ${{{\Sigma }}_{{\rm mix}}}$, the mass fraction of helium in the mixed layer is decreased to be

$$\begin{eqnarray}&&{{Y}_{{\rm mix}}}={{Y}_{0}}{{{\Sigma }}_{{\rm acc}}}/{{{\Sigma }}_{{\rm mix}}},\end{eqnarray} \tag{ 11 }$$

where Y₀ is the initial helium fraction of the material when it is first accreted (this variable is introduced just for completeness, I always use ${{Y}_{0}}=1$). Similarly, the C/O, which have mass fractions of X₁₂ and X₁₆ in the C/O core, will be mixed up and have mass fractions

$$\begin{eqnarray}&&{{X}_{12,{\rm mix}}}={{X}_{12}}(1-{{{\Sigma }}_{{\rm acc}}}/{{{\Sigma }}_{{\rm mix}}}),\end{eqnarray} \tag{ 12 }$$

and

$$\begin{eqnarray}&&{{X}_{16,{\rm mix}}}={{X}_{16}}(1-{{{\Sigma }}_{{\rm acc}}}/{{{\Sigma }}_{{\rm mix}}})\end{eqnarray} \tag{ 13 }$$

in the mixed layer.

The Kelvin–Helmholtz instability (also referred to as the dynamical shear instability) is governed by the Richardson number

$$\begin{eqnarray}&&Ri\equiv \frac{{{N}^{2}}}{{{\sigma }^{2}}},\end{eqnarray} \tag{ 14 }$$

where N is the Brunt–Väisälä frequency

$$\begin{eqnarray}&&{{N}^{2}}=\frac{g}{H}\frac{{{\chi }_{T}}}{{{\chi }_{\rho }}}\left[ {{\nabla }_{{\rm ad}}}-{{\left( \frac{d{\rm ln} T}{d{\rm ln} P} \right)}_{*}} \right],\end{eqnarray} \tag{ 15 }$$

where ${{\chi }_{Q}}=\partial {\rm ln} P/\partial {\rm ln} Q$, with all other intensive variables set constant, ${{\nabla }_{{\rm ad}}}={{(\partial {\rm ln} T/\partial {\rm ln} P)}_{{\rm ad}}}$ is the adiabatic temperature gradient, and the star refers to derivatives of the envelope's profile. This is just the thermal contribution to the buoyancy, and it is estimated to be (Bildsten 1998)

$$\begin{eqnarray}&&N\approx {{\left( \frac{3}{20}\frac{g}{H} \right)}^{1/2}}=2.6T_{8}^{-1/2}\;{{{\rm s}}^{-1}}.\end{eqnarray} \tag{ 16 }$$

Note that for the scalings presented in this section I focus on the thermodynamic properties of the surface layers and omit the scalings with the WD mass, radius, and composition for simplicity. These scalings all assume $M=1\;{{M}_{\odot }}$, $R=5\times {{10}^{8}}\;{\rm cm}$, and a helium-rich composition, but I consider changes from these WD properties in the numerical investigation later. Linear analysis shows that Kelvin–Helmholtz instability occurs when ${\rm Ri}\lt 1/4$, which develops into strong turbulence that readily transports angular momentum.

The condition for instability of ${\rm Ri}\lt 1/4$ assumes that thermal diffusion can be ignored for the unstable fluid perturbations, in other words, that the perturbations are adiabatic. Fluid perturbations with a characteristic size L and speed V become non-adiabatic when the timescale for thermal diffusion, ${{L}^{2}}/K$, where K is the thermal diffusivity, is less than the timescale of the perturbation, $L/V$. The ratio of these two timescales is the Péclet number, ${\rm Pe}\equiv VL/K$ (Townsend 1958). The restoring force provided by thermal buoyancy is weakened when ${\rm Pe}\lt 1$, which requires the substitution of ${{N}^{2}}\to {\rm Pe}{{N}^{2}}$ and promotes instability. Thermal diffusion is most efficient at small lengthscales, which motivates setting $LV/{{\nu }_{k}}={{\operatorname{Re}}_{c}}$ (Zahn 1992), where ${{\nu }_{k}}$ is the kinematic viscosity and Re_c is the critical Reynolds number for turbulence, which is of order 1000. This gives the Péclet number approximately related to the Prandtl number, Pr, by ${\rm Pe}\approx {{\operatorname{Re}}_{c}}{\rm Pr}$. The turbulent perturbations are thus non-adiabatic when (Zahn 1992)

$$\begin{eqnarray}&&K\gt {{\nu }_{k}}{{\operatorname{Re}}_{c}}.\end{eqnarray} \tag{ 17 }$$

In the non-degenerate surface layers the kinematic viscosity is dominated by ions, and has a value of (Spitzer 1962)

$$\begin{eqnarray}&&{{\nu }_{k}}=1.4\times {{10}^{-2}}\rho _{5}^{-1}T_{8}^{5/2}\;{\rm c}{{{\rm m}}^{2}}\;{{{\rm s}}^{-1}},\end{eqnarray} \tag{ 18 }$$

where ${{\rho }_{5}}\equiv \rho /{{10}^{5}}\;{\rm g}\;{\rm c}{{{\rm m}}^{-3}}$, and I assume a Coulomb logarithm of ${\rm ln} {\Lambda }=20$. Setting $K=16{{\sigma }_{{\rm SB}}}{{T}^{3}}/(3{{c}_{p}}\kappa {{\rho }^{2}})$, where ${{\sigma }_{{\rm SB}}}$ the Stefan–Boltzmann constant, c_p the specific heat, and κ the opacity, the thermal diffusivity is

$$\begin{eqnarray}&&K=980\kappa _{0.2}^{-1}\rho _{5}^{-2}T_{8}^{3}\;{\rm c}{{{\rm m}}^{2}}\;{{{\rm s}}^{-1}},\end{eqnarray} \tag{ 19 }$$

where I approximate ${{c}_{p}}=5{{k}_{{\rm B}}}/2\;\mu {{{\rm m}}_{p}}$ and scale the opacity to ${{\kappa }_{0.2}}\equiv \kappa /0.2\ {\rm c}{{{\rm m}}^{2}}\;{{{\rm g}}^{-1}}$, appropriate for electron scattering in hydrogen-deficient material. Substituting Equations (18) and (19) into Equation (17), I find that the perturbations are non-adiabatic at depths of $\rho \lesssim 7\times {{10}^{6}}\;{\rm g}\;{\rm c}{{{\rm m}}^{-3}}\;T_{8}^{1/2}$. The new "secular" Richardson number associated with this limit is,

$$\begin{eqnarray}&&{\rm R}{{{\rm i}}_{s}}\equiv \frac{{{\nu }_{k}}{{\operatorname{Re}}_{c}}}{K}\frac{{{N}^{2}}}{{{\sigma }^{2}}}.\end{eqnarray} \tag{ 20 }$$

When ${\rm R}{{{\rm i}}_{s}}\lt 1/4$, the so-called "secular shear instability" arises.

The competing effects of accretion increasing σ versus turbulence developing when ${\rm R}{{{\rm i}}_{s}}\lt 1/4$ (and decreasing σ) drive the surface layers toward marginally satisfying ${\rm R}{{{\rm i}}_{s}}=1/4$ (assuming for the moment that the sole viscous mechanism is the Kelvin–Helmholtz instability). This expectation is borne out in the WD studies of Yoon & Langer (2004b). Thus I estimate the q due to this mechanism. Substituting ${\rm R}{{{\rm i}}_{s}}=1/4$ into Equation (20), and assuming Re_c = 1000, the shear rate is

$$\begin{eqnarray}&&{{\sigma }_{{\rm KH}}}=2.0\kappa _{0.2}^{1/2}\rho _{5}^{1/2}T_{8}^{-3/4}\;{{{\rm s}}^{-1}}.\end{eqnarray} \tag{ 21 }$$

A shear rate this large is similar to the Keplerian frequency given by Equation (1), but as I show next, other fluid instabilities limit the shear before it can reach such a large value.

The baroclinic instability arises because surfaces of constant pressure and density no longer coincide if hydrostatic balance is to be maintained when differential rotation is present. In such a configuration, fluid perturbations along nearly horizontal directions are unstable, though with a sufficient radial component to allow mixing of angular momentum and material. The instability can roughly be broken into two limits, depending on a critical baroclinic Richardson number (Fujimoto 1987),

$$\begin{eqnarray}&&{\rm R}{{{\rm i}}_{{\rm BC}}}\equiv 4{{\left( \frac{R}{H} \right)}^{2}}{{\left( \frac{{\Omega }}{N} \right)}^{2}}=10.7T_{8}^{-1}{\Omega }_{0.1}^{2},\end{eqnarray} \tag{ 22 }$$

where ${{{\Omega }}_{0.1}}={\Omega }/0.1\;{{{\rm s}}^{-1}}$. When ${\rm Ri}\gt {\rm R}{{{\rm i}}_{{\rm BC}}}$, Coriolis effects limit the horizontal scale of perturbations. This results in two parameterizations for viscosity estimated from linear theory (Fujimoto 1993),

$$\begin{eqnarray}{{\nu }_{{\rm BC}}}=\left\{ \begin{array}{ccccccccccccccc} \frac{{{\alpha }_{{\rm BC}}}}{3}\frac{1}{{\rm R}{{{\rm i}}^{1/2}}}{{H}^{2}}{\Omega }, & {\rm Ri}\leqslant {\rm R}{{{\rm i}}_{{\rm BC}}}, \\ \frac{{{\alpha }_{{\rm BC}}}}{3}\frac{{\rm R}{{{\rm i}}_{{\rm BC}}}}{{\rm R}{{{\rm i}}^{3/2}}}{{H}^{2}}{\Omega }, & {\rm Ri}\gt {\rm R}{{{\rm i}}_{{\rm BC}}}, \\ \end{array} \right.\end{eqnarray} \tag{ 23 }$$

where I include a dimensionless factor ${{\alpha }_{{\rm BC}}}$, to account for uncertainty in how linear theory relates to the saturated amplitudes of the instability. In general, I find ${{\alpha }_{{\rm BC}}}\lesssim 1$ is required for significant mixing, which I explain in more detail below.

By substituting ${{\nu }_{{\rm BC}}}$ into Equation (6), I solve for the shearing profile. Due to the relatively low ${\rm R}{{{\rm i}}_{{\rm BC}}}$ for WDs, see Equation (22), it is almost always the case that ${\rm Ri}\gt {\rm R}{{{\rm i}}_{{\rm BC}}}$. Thus, using the second of the two viscosity prescriptions I find

$$\begin{eqnarray}&&{\rm Ri}=3.6\times {{10}^{4}}\alpha _{{\rm BC}}^{1/2}\rho _{5}^{1/2}T_{8}^{1/4}{\Omega }_{0.1}^{3/2}\dot{M}_{-6}^{-1/2},\end{eqnarray} \tag{ 24 }$$

where ${{\dot{M}}_{-6}}=\dot{M}/{{10}^{-6}}\;{{M}_{\odot }}\;{\rm y}{{{\rm r}}^{-1}}$. This demonstrates directly that ${\rm Ri}\gg {\rm R}{{{\rm i}}_{{\rm BC}}}$ for accreting WDs. The shear is

$$\begin{eqnarray}&&{{\sigma }_{{\rm BC}}}=1.4\times {{10}^{-2}}\alpha _{{\rm BC}}^{-1/4}\rho _{5}^{-1/4}T_{8}^{-5/8}{\Omega }_{0.1}^{-3/4}\dot{M}_{-6}^{1/4}\;{{{\rm s}}^{-1}},\end{eqnarray} \tag{ 25 }$$

This demonstrates a couple of key features of the shear. First, it is higher for large accretion rates, which makes perfect sense because angular momentum is being added more quickly to the star. Second, it is smaller for higher spin rates. This is because the baroclinic instability becomes stronger when the WD is spinning faster, which leads to a smoothing out of the shearing. Also note that generally ${{\sigma }_{{\rm BC}}}\ll {{\sigma }_{{\rm KH}}}$, so that the baroclinic instability triggers before the Kelvin–Helmholtz instability. This prevents the shear rate from ever becoming large enough for the Kelvin–Helmholtz instability to operate at depths of $\rho \gtrsim 100\ {\rm g}\;{\rm c}{{{\rm m}}^{-3}}$, i.e., at depths critical for unstable helium ignition.

The shear and dissipation by viscosity also leads to viscous heating within the accreted layer. The heating rate per unit mass is

$$\begin{eqnarray}&&\epsilon =\nu {{\sigma }^{2}}/2,\end{eqnarray} \tag{ 26 }$$

which for the shearing estimates given above results in

$$\begin{eqnarray}&&{{\epsilon }_{{\rm BC}}}=6.9\times {{10}^{2}}\alpha _{{\rm BC}}^{-1/4}\rho _{5}^{-5/4}T_{8}^{-5/8}{\Omega }_{0.1}^{-3/4}\dot{M}_{-6}^{5/4}\;{\rm erg}\;{{{\rm g}}^{-1}}{{{\rm s}}^{-1}}.\end{eqnarray} \tag{ 27 }$$

To put this in context, it is helpful to multiply this result by the accretion timescale ${{t}_{{\rm acc}}}$ to roughly give the total energy per nucleon accreted

$$\begin{eqnarray}&&{{E}_{{\rm BC}}}\approx 0.04\alpha _{{\rm BC}}^{-1/4}\rho _{5}^{-1/4}T_{8}^{3/8}{\Omega }_{0.1}^{-3/4}\dot{M}_{-6}^{1/4}\;{\rm keV}\;{\rm nuc}{{{\rm l}}^{-1}}.\end{eqnarray} \tag{ 28 }$$

In comparison, the thermal energy at the base of the accreted layer is about $\approx 10\;{\rm keV}\;{\rm nuc}{{{\rm l}}^{-1}}$. This means that viscous heating is usually not important, but can be for especially low values of ${{\alpha }_{{\rm BC}}}$ and Ω (as can be see in discussions by Yoon & Langer 2004a, but in the context of shear instabilities). For the remainder of this work I ignore viscous heating so as to focus on the impact of mixing, but heating should be included in a fuller, more self-consistent calculation.

The turbulence that transports angular momentum also mixes material, albeit with much less efficiency because it requires more work to exchange fluid elements than to just exert stresses. Energy arguments give a mixing diffusivity that is related to the viscosity by (Piro & Bildsten 2007)

$$\begin{eqnarray}&&D\approx \nu /{\rm Ri},\end{eqnarray} \tag{ 29 }$$

where there is a correction of order unity in this relation (often referred to as the flux Richardson number Rf), which I ignore for simplicity. I already have one free parameter in ${{\alpha }_{{\rm BC}}}$ to adjust the strength of the turbulence (although this does not allow me to vary the angular momentum and material mixing independently).

For this mixing diffusivity, I can now evaluate the mixing time as a function of depth using Equation (10), resulting in

$$\begin{eqnarray}&&{{t}_{{\rm mix}}}=2.1\times {{10}^{4}}\alpha _{{\rm BC}}^{1/4}\rho _{5}^{5/4}T_{8}^{13/8}{\Omega }_{0.1}^{3/4}\dot{M}_{-6}^{-5/4}\;{\rm yr}.\end{eqnarray} \tag{ 30 }$$

In comparison, the accretion time down to a similar depth is

$$\begin{eqnarray}&&{{t}_{{\rm acc}}}=4\pi {{R}^{2}}\;H\rho /\dot{M}=1.9\times {{10}^{3}}{{\rho }_{5}}{{T}_{8}}\dot{M}_{-6}^{-1}\;{\rm yr}.\end{eqnarray} \tag{ 31 }$$

This shows that ${{t}_{{\rm mix}}}$ and ${{t}_{{\rm acc}}}$ are somewhat comparable for reasonable parameters, motivating that mixing is potentially important. Furthermore, since ${{t}_{{\rm mix}}}/{{t}_{{\rm acc}}}\propto {{\dot{M}}^{-1/4}}$, the mixing gets stronger as the accretion rate increases. Conversely, the scalings with density argue that mixing is only effective in the layers sufficiently shallow that ${{t}_{{\rm mix}}}\lt {{t}_{{\rm acc}}}$ or when

$$\begin{eqnarray}&&\rho \lt 5.9\alpha _{{\rm BC}}^{-1}T_{8}^{-5/32}{\Omega }_{0.1}^{-3}{{\dot{M}}_{-6}}\;{\rm g}\;{\rm c}{{{\rm m}}^{-3}}.\end{eqnarray} \tag{ 32 }$$

This relatively small number for ρ means that both the viscosity parameter must be small ${{\alpha }_{{\rm BC}}}\sim {{10}^{-2}}$ and the spin must be relatively small ${\Omega }\sim {{10}^{-2}}{{{\Omega }}_{K}}$ for mixing to happen. This motivates the values I use for these parameters for the numerical calculations in the next section. In particular, the large exponent of ${{{\Omega }}^{-3}}$ shows that the spin plays an especially important role in determining whether mixing is occurring. Also, note that the mixing I find here is never as large as what Yoon et al. (2004) calculate when focusing on the secular shear instability. This means that I also do not find solutions where the helium is mixed sufficiently enough to prevent unstable shell ignition.

To make this scheme more concrete, it is helpful to to consider a specific example of the time evolution of an envelope as it accretes toward unstable ignition. This example is for a $M=1\;{{M}_{\odot }}$ WD accreting at a rate $\dot{M}={{10}^{-6}}\;{{M}_{\odot }}\;{\rm y}{{{\rm r}}^{-1}}$. A reasonable ignition mass for such conditions is ${{M}_{{\rm ign}}}\approx 3.0\times {{10}^{-3}}\;{{M}_{\odot }}$ (Iben & Tutukov 1989; Shen & Bildsten 2009). For the mixing, I set the WD spin to be ${\Omega }=0.01{{{\Omega }}_{K}}$ and use ${{\alpha }_{{\rm BC}}}=0.01$.

Figure 2 shows four different moments in time as the WD accretes and builds a surface layer of accreted material mixed with C/O from the WD surface. In each panel, the amount of time for which the WD has been accreting ${{t}_{{\rm acc}}}$ is denoted along with the total mass fraction of C/O mixed into the surface layer. The solid line shows the temperature profile down to the base of the layer, with the solid circle denoting the amount of material that was actually accreted (much like the horizontal dashed line in Figure 1). The dashed curve is the stability criterion given by Equation (33). In the bottom right panel the surface temperature profile now extends down to this ignition curve demonstrating that this model will now ignite.

Zoom In Zoom Out Reset image size

A number of important features and trends caused by the mixing, that were described previously in my analytic exploration in Section 2, are now made more clear by this numerical example. These are as follows.

• 1.  
  Mixing is strongest at earlier times and decreases the longer the accretion persists until ignition (as can be seen by the mixed C/O mass fraction decreasing with time). This because it gets more and more difficult to mix to larger depths.
• 2.  
  Mixing causes unstable ignition of the surface layer in a larger mass of material for a given accretion rate than without mixing. In this case the mass of the surface layer is $3.4\times {{10}^{-3}}\;{{M}_{\odot }}$ at the moment of ignition after accreting $2.1\times {{10}^{-3}}\;{{M}_{\odot }}$ of helium. This is $\approx 13\%$ more mass in the surface layer than the unmixed case.
• 3.  
  Igniting deeper also decreases the time to accrete until ignition, in this case by $\approx 30\%$ from $\approx 3\times {{10}^{3}}\;{\rm yr}$ down to $\approx 2.1\times {{10}^{3}}\;{\rm yr}$.

Most importantly of all, this demonstrates that it is reasonable for ignition to occur in a fairly mixed environment. In this case, ${{Y}_{{\rm mix}}}=0.62$ while the mass fraction of C/O is 0.38. This hopefully motivates the investigation of similarly mixed conditions in future surface burning models (e.g., Shen & Moore 2014).

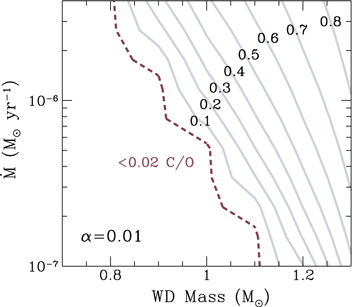
To further illustrate the trends of the mixing, I explore the amount of mixing as a function of the accretion rate and WD spin. In Figure 3, I use $M=1\;{{M}_{\odot }}$, $R=5\times {{10}^{8}}\;{\rm cm}$, and ${{\alpha }_{{\rm BC}}}=0.01$ and plot contours of the mass fraction of C/O. This shows there is quite a range of mixing, from nearly unmixed on the right side of the plot to fully 90% C/O on the left side.

Zoom In Zoom Out Reset image size

The general trend is that more mixing occurs at high accretion rates and low WD spin. The impact of a high accretion is intuitively clear, because if more angular momentum and material is added more quickly it is reasonable to expect more mixing. Less clear is why slower spin leads to more mixing. The first thing to note is that it is not because there is a larger shear between the WD and the accreted material; the total change in spin is basically the same whether ${\Omega }=0.001{{{\Omega }}_{K}}$ or $0.01{{{\Omega }}_{K}}$. It is instead because the viscosity scales with the spin as shown in Equation (23). As the WD spins higher, surfaces of constant pressure and density become more and more misaligned, which in turn drives the baroclinic instability and turbulent viscosity associated with it. A higher viscosity results in a smaller shear to transport the angular momentum, as shown in Equation (6), and less shear leads to less mixing. Conversely, for small spin and turbulent viscosity, the shear is large and thus the mixing with it. This is particularly striking in Figure 3, where to the right of the dashed line there is quite little mixing.

Since the analytic estimates showed a strong dependence on ${{\alpha }_{{\rm BC}}}$ in Equation (32), I present the mixed C/O mass fractions for ${{\alpha }_{{\rm BC}}}=0.1$ in Figure 4. This roughly moves all the curves to the left and up, showing how much more difficult it is to mix when the viscosity is higher. This is simply because there is less shear and turbulence in this case. For ${{\alpha }_{{\rm BC}}}\sim 1$ there is little mixing except in the most extreme circumstances (of high accretion rate and low spin), and thus it is possible that turbulent mixing is negligible depending on what the real turbulent viscosity should be.

Zoom In Zoom Out Reset image size

As mentioned in the example calculation above, the mixing also causes ignition deeper than without mixing. This is quantified further in Figure 5, where I plot contours of constant ignition mass. This shows that at fixed accretion rate, the ignition mass goes up for lower spin (i.e., moving to the left). At fixed spin, the ignition mass goes down for higher accretion rate just as in the non-mixed case, but just not by as much.

Zoom In Zoom Out Reset image size

The strength of the mixing should also depend on the mass and radius of the WD. To explore this, I repeat my analysis of for the amount of mixing which is summarized in Figure 6. This shows that there is in fact a strong dependence on mass. This can be understood from two main factors. First, the Keplerian spin of the incoming material is larger with larger mass, which means a larger amount of angular momentum needs to be carried through the star. Second, the larger surface gravity in turn results in a smaller scale height H in the surface layers. This weakened the turbulent viscosity, leading to a larger shear and more mixing.

Zoom In Zoom Out Reset image size