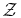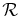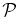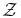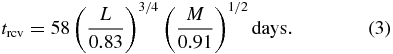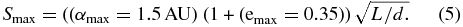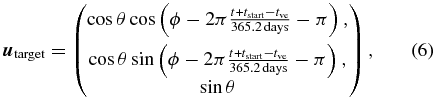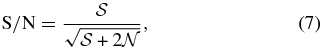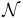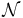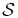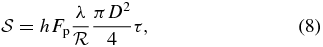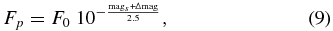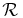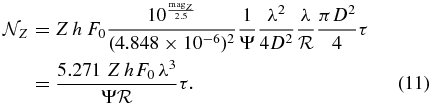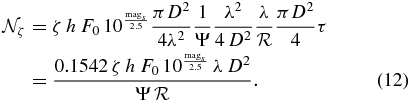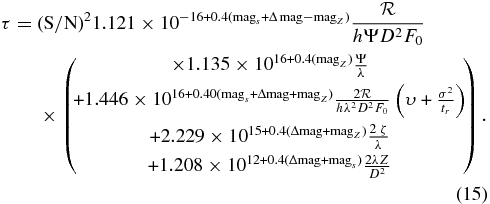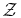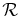SCIENCE PARAMETRICS FOR MISSIONS TO SEARCH FOR EARTH-LIKE EXOPLANETS BY DIRECT IMAGING

Teams of astronomers and optical experts are now designing future space telescopes and instruments for high-dynamic-range imaging to search for extrasolar planets. The goal is to find and characterize Earth-like planets, with the size, atmospheric composition, and temperature of Earth—possible habitats of life. Terrestrial Planet Finder is the prototype of such missions: aperture in the range D = 4–64 m; a nominal operating wavelength λ = 760 nm, which allows diagnostic spectroscopy of methane and oxygen; inner working angle IWA = 0.02–0.31'', which is the effective radius of the central field obscuration; and starlight suppression ζ = 10⁻⁷ to 10⁻¹¹ by an internal coronagraph, where ζ is the intensity of scattered starlight expressed in units of the theoretical central intensity of the stellar Airy disk.

Because of the great expense and technical challenge of mounting a mission like Terrestrial Planet Finder, competing concepts must be tested with a science metric that probes the many optical and operational issues. The most compelling science metric for this purpose is the estimated number of planets N_t that would be discovered in mission time t.

The goals of metrical analysis are at least threefold: to better understand the basic character of such a complex mission with many moving parts, to inform tradeoffs and reductions of scope in a cost-sensitive environment, and to set expectations that could reasonably be fulfilled if a mission is implemented.

This paper reports a parametric analysis using the formalism of the design reference mission, which is an optimized list of observations that simulate the mission as a whole, including random discoveries. In particular, we use design reference missions to estimate N as a function of 27 mission parameters, which are divided into three categories: 2 are astronomical, 7 are instrumental, and 18 are science-operational. (See Table 1.) We use the term "27-vector" to refer to a complete set of values for this set of 27 mission parameters.

Table 1. 27 Parameters of Science Metric N

		Parameter	Symbol	Baseline Value	Range	Units
	1	Occurrence probability	ηtrue	0.20	0.05–0.8
Astronomical
	2	Zodi	Z	7	0.875–56	23 mag arcsec−2
	3	Aperture	D	16	4–64	m
	4	Inner working angle	IWA	0.039	0.02–0.31	arcsec
	5	Sharpness	Ψ	0.08
Instrumental	6	End-to-end efficiency	h	0.2	0.05–0.80
	7	Dark noise	υ	0.00055		counts s−1
	8	Read noise	σ	2.8		√counts/read
	9	Scattered starlight	ζ	10−10	10−7 to 10−11	Airy peak intensity
	10	Operational wavelength	λ	760		Nm
	11	Limiting delta magnitude	Δmag0	26	23–27.5
	12	Observational overhead	o/h	0.5	0–2	Days
	13	Readout cadence	r	2000		s
	14	Resolution, imaging	${\cal R}$img	5
	15	Resolution, spectroscopy	${\cal R}$spc	70	17.5–280
	16	S/N, imaging	S/Nimg	8
	17	S/N, spectroscopy	S/Nspc	8	8–160
	18	Rolls	q	1
Science operational
	19	Mission start	tstart	2460310 (1/1/2024)		Julian day
	20	Mission duration	tstart–tstop	5 (1826)		yr (days)
	21	Planetary radius	R	1		Earth radii
	22	Geometric albedo	p	0.3
	23	Semimajor axis	a	(0.7–1.5) √L		AU
	24	Eccentricity	e	0–0.35
	25	Solar avoidance angle	γ1	45°		deg
	26	Antisolar avoidance angle	γ2	180°		deg
	27	Mission time	t	1826	0 ⩽ t ⩽ 1826	days

Notes. a and e are assigned random values uniformly distributed in the indicated rages. The pole of the orbit is distributed uniformly on the sphere.

Download table as:  ASCIITypeset image

Our model treats a variety of science-operational aspects, including (1) waiting for available completeness c to recover after a limiting search observation that did not detect a planet (Brown & Soummer 2010); (2) solar and antisolar pointing avoidance; (3) overhead time t_o/h per observation; and (4) "filler" days that could be used for other observing programs when no candidate target star is searchable—a situation that can occur for a short input catalog when all candidate targets are either forbidden by the pointing restrictions or are still waiting for completeness c to recover.

A limiting search observation is an exposure to reach the systematic limit of detection, Δmag₀, such that detecting a fainter source is assumed not to be possible. Δmag is the flux ratio between star and planet expressed in stellar magnitudes.

Completeness c is defined as the fraction of planets of interest that would be detected according to two criteria: s > IWA, which means the planet is not obscured (Brown 2004a), and Δmag < Δmag₀, which means that the planet is brighter than the noise floor (Brown 2005). The apparent separation s is the angle between the planet and the host star as seen by the observer.

The purpose of solar and antisolar pointing restrictions is to avoid sunlight scattering into the optical path of the target star during an exposure. In the general case, pointing might be restricted in both the solar and antisolar directions.

Our baseline 27-vector is a mission with D = 16 m, IWA = 0.039'', t = 0–5 yr, occurrence probability η = 0.2, and typical values for the other 23 parameters. A design reference mission for the baseline case involves ∼4700 candidate stars with nonzero completeness, ∼1300 unique stars observed in 2600 observations, of which 1300 are revisits, and produces an estimated N₁ ∼ 50 exoplanets after one year and N₅ = 130 after five years of elapsed mission time. These statistics vary for parameters away from the baseline.

To investigate the parametric variations of the science metric N, we compute design reference missions for a suite of diagnostic 27-vectors in the vicinity of the baseline. In Section 2, we define and describe the components of our computations—a mise en place. In Section 3, we give the step-by-step recipe for computing a design reference mission and estimating N. In Section 4, we summarize our findings, and in Section 5 we offer conclusions.

In days of yore, every observatory dome had a logbook in which the observer recorded, usually in ink, each observation with the telescope—object name, celestial coordinates, instrument used, exposure time, universal time, and comments, which were often about the weather. Each entry in the logbook also had an unrecorded backstory: why a target was selected and what was already known about it. A follow-on narrative was also implied but unrecorded: the results after data reduction, calibration, and analysis. To better understand the research reported here, about a great space telescope of the future, it may be helpful from time to time to ponder the analogy between an old-time logbook and a design reference mission. We could start by noting that each of the 27 parameters in Table 1 has a valid counterpart in the classical setting. Other correspondences will come to mind, such as between the old-time observer in the telescope dome and the scheduling algorithm.

2.1. Engine for Design Reference Missions

Our engine for producing design reference missions is actually Mathematica computer code. The input to the code is a 27-vector, and the output is a design reference mission, including results for N_t. The design reference mission is literally a table—here, table with 12 columns—with as many rows as the number of observations it describes. Each row comprises 12 data items: (1) Hipparcos number HIP; (2) mission day t on which the observation is performed; (3) the number of visits to this target up to now; (4) the value of c for this observation (Brown 2005); (5) the total completeness C harvested by all searches of this targetup until now; (6) the Bayesian probability

$$\begin{equation} \mathcal{P}\equiv \frac{\eta c}{1-\eta C} \end{equation} \tag{ 1 }$$

that this observation will discover a planet (Brown & Soummer 2010); (7) whether a planet is in fact discovered, true or false, as determined by a draw from a Bernoulli random deviate of probability $\mathcal{P}$; (8) total discoveries by all observationsuntil now; (9) the merit function for this observation

$$\begin{equation} {\cal Z} \equiv \frac{\mathcal{P}}{{\tau _{{\rm LSO}} + t_{\rm o/h} }}; \end{equation} \tag{ 2 }$$

(10) exposure time τ_LSO of a limiting search observation (see Section 2.10); (11) the actual exposure time τ_spc, including spectroscopy if a planet has been discovered; and (12) the total time cost of the observation, including observational overhead (see Section 2.7).

η is the assumed occurrence rate of the planets of interest. $\mathcal{Z}$ might be called the information rate, discovery rate, or benefit-to-cost ratio of the observation.

Table 1 is a list of the parameters in a 27-vector and the values they take on in the baseline.

Table 2 is a truncated example of a design reference mission for the baseline, giving the first 10 and last 10 lines.

Table 2. Typical Five-Year Design Reference Mission for the Baseline Parameters (Truncated)

Observation	HIP	t	Visits	c	C	$\mathcal{P}$	Discovery	Total discoveries	$\mathcal{Z}$	τLSO	τ	Total time cost
1	16537	0.5	1	0.875	0.875	0.175	Yes	1	0.346	0.006	0.001	0.501
2	104214	1	1	0.895	0.895	0.179	No	1	0.344	0.02	0.02	0.52
3	8102	1.5	1	0.849	0.849	0.169	No	1	0.335	0.005	0.005	0.505
4	71681	2	1	0.833	0.833	0.166	Yes	2	0.333	0	0	0.5
5	19849	2.5	1	0.854	0.854	0.17	No	2	0.333	0.013	0.013	0.513
6	19849	2.5	1	0.854	0.854	0.17	No	2	0.333	0.013	0.013	0.513
7	104217	3	1	0.883	0.883	0.176	No	2	0.332	0.03	0.03	0.53
8	96100	3.5	1	0.842	0.842	0.168	No	2	0.325	0.017	0.017	0.517
9	88601	4	1	0.814	0.814	0.162	No	2	0.32	0.008	0.008	0.508
10	99461	4.6	1	0.838	0.838	0.167	No	2	0.314	0.033	0.033	0.533
...	...	...	...	...	...	...	...	...	...	...	...	...
2567	67155	1819.2	1	0.259	0.259	0.051	No	133	0.035	0.972	0.972	1.472
2568	12447	1819.9	3	0.115	0.501	0.025	No	133	0.036	0.193	0.193	0.693
2569	20215	1820.8	1	0.156	0.156	0.031	No	133	0.035	0.375	0.375	0.875
2570	86184	1821.5	3	0.109	0.435	0.023	No	133	0.035	0.166	0.166	0.666
2571	114834	1822.3	1	0.147	0.147	0.029	No	133	0.035	0.337	0.337	0.837
2572	86815	1823	2	0.126	0.294	0.026	No	133	0.035	0.245	0.245	0.745
2573	57841	1823.6	4	0.09	0.766	0.02	No	133	0.035	0.091	0.091	0.591
2574	99701	1824.5	2	0.148	0.541	0.032	No	133	0.036	0.382	0.382	0.882
2575	19758	1825.4	1	0.147	0.147	0.029	No	133	0.035	0.329	0.329	0.829
2576	101966	1826	3	0.109	0.613	0.024	No	133	0.035	0.193	0.193	0.693

Notes. HIP is the Hipparcos number. t is the current time in mission days. c is the completeness of this observation. C is the total completeness so far, including c. $\mathcal{P}$ is the probability of a discovery by this observation. $\mathcal{Z}$ is the merit function of this observation. τ_LSO is the exposure time for a limiting search observation, in days. τ is the actual exposure time in days. The last column is the total time cost in days includes overhead. The zeros in Line 4 mean "< 10⁻³ days."

Download table as:  ASCIITypeset image

Table 3 summarizes the results of design reference missions for the baseline and diagnostic offsets of the primary parameters, D and IWA. To build Table 3, we compute 240 design reference mission ab initio for each 27-vector and averaged the results.

Table 3. Design Reference Mission Results for Major Parameters D and IWA Near the Baseline

Case	D	IWA	λ/D	Observations	Revisits	Fill	Stars in	Stars obs	N1	N5
1	128	0.04''	16	3620	0	0	16873	3620	105.2	372.1
2	64	0.04''	8	3507	0	0	16869	3507	103.6	366.1
3	32	0.04''	4	2999	0	0	16866	2999	95.6	323.5
4	64	0.04''	16	3600	1944	0	4719	1656	64.2	153.7
5	32	0.04''	8	3409	1822	0	4721	1587	61.4	147.5
6	16	0.04''	4	2609	1338	0	4721	1271	54.8	128.7
7	64	0.08''	32	3632	3162	0	598	470	23.6	39.0
8	32	0.08''	16	3564	3103	0	594	461	23.3	38.3
9	16	0.08''	8	3227	2785	0	597	442	22.8	38.2
10	8	0.08''	4	2041	1690	0	591	351	19.9	35.1
11	4	0.08''	2	702	493	0	590	209	12.0	23.3
12	64	0.16''	64	1185	1108	1233	77	77	3.4	4.9
13	32	0.16''	32	1200	1122	1222	78	78	3.4	4.8
14	16	0.16''	16	1215	1136	1197	79	79	3.5	5.1
15	8	0.16''	8	1192	1114	1101	78	78	3.5	5.0
16	4	0.16''	4	1145	1067	51	78	78	3.2	4.6
17	32	0.31''	64	132	124	1766	8	8	0.4	0.6
18	16	0.31''	32	128	120	1768	8	8	0.4	0.6
19	8	0.31''	16	123	115	1769	8	8	0.5	0.6
20	4	0.31''	8	119	111	1758.7	8	8	0.4	0.6

Notes. Each line is the average of 240 design reference missions with the same parameters. Line 6: baseline case. Lines 9–11: cases neighboring the baseline. Other lines: other cases of D and IWA selected to explore the parametrics in the vicinity of the baseline. "Stars in" means all stars in the input catalog with nonzero completeness. "Stars obs" means all unique stars that are observed at least once in a typical design reference mission.

Download table as:  ASCIITypeset image

Tables 4–11 summarize the results for diagnostic offsets for eight secondary parameters.

Table 4. Results for Offsets of Occurrence Probability η

η	N1	N5	Observations	Stars	Revisits
0.8	212	517	2207	1071	1136
0.4	106	254	2467	1212	1255
0.2	54	129	2612	1272	1340
0.1	29	67	2685	1297	1388
0.05	14	31	2736	1309	1427

Download table as:  ASCIITypeset image

Table 5. Results for Offsets of Zodiacal Light Z

Z	N1	N5	Observations	Stars	Revisits
0	60	144	2864	1420	1444
3.5	54	139	2627	1273	1354
7	56	131	2703	1323	1380
14	54	125	2571	1263	1308
25	52	121	2233	1076	1157
50	47	106	1952	947	1005
100	43	95	1665	798	867
200	36	79	1373	675	698

Download table as:  ASCIITypeset image

Table 6. Results for Offsets of End-to-end Efficiency h

H	N1	N5	Observations	Stars	Revisits
0.8	59	144	3289	1531	1758
0.4	58	138	3015	1426	1589
0.2	55	129	2609	1271	1338
0.1	46	108	2080	1057	1023
0.05	39	91	1484	810	674

Download table as:  ASCIITypeset image

Table 7. Results for Offsets of Scattered Light ζ

	N1	N5	Observations	Stars	Revisits
10−11	57	133	2831	1340	1491
10−10	55	128	2606	1274	1332
10−9	41	97	1604	900	704
10−8	19	44	533	366	167
10−7	6	12	136	102	34

Download table as:  ASCIITypeset image

Table 8. Results for Offsets of Observational Overhead t_o/h

to/h	N1	N5	Observations	Stars	Revisits
0	114	207	8067	1890	6177
0.125	90	177	5388	1621	3767
0.25	72	155	4003	1473	2530
0.5	55	129	2609	1271	1338
1	38	96	1538	1011	527
2	23	68	841	748	93

Download table as:  ASCIITypeset image

Table 9. Results for Offsets of the Noise Floor Δmag₀

Δmag0	N1	N5	Observations	Stars	Revisits
27.5	43	104	1030	822	208
27.0	54	126	1505	1044	461
26.5	57	134	2069	1203	866
26.0	55	129	2609	1271	1338
25.5	50	110	3054	1129	1925
25.0	40	86	3337	917	2420
24.0	23	43	3567	489	3078
23.0	10	15	3627	203	3424

Download table as:  ASCIITypeset image

Table 10. Results for Offsets of the Spectroscopic Resolving Power ${\cal R}$_spc

${\cal R}$spc	N1	N5	Observations	Stars	Revisits
17.5	56	135	2772	1305	1467
35.0	55	129	2730	1298	1432
70.0	55	129	2609	1271	1338
140.	50	120	2321	1190	1131
280.	42	101	1666	1000	666

Download table as:  ASCIITypeset image

Table 11. Results for Offsets of Spectroscopic Signal-to-noise Ratio S/N_spc

S/Nspc	N1	N5	Observations	Stars	Revisits
8	55	129	2610	1270	1340
20	46	108	1890	1066	824
40	35	80	1050	771	279
80	20	43	434	433	1
160	10	22	205	205	0

Download table as:  ASCIITypeset image

2.2. Scheduling Algorithm

2.3. Two Types of Observations

2.4. Completeness

Through the detection probability $\mathcal{P}$ and the merit function ${\cal Z}$ in Equations (1) and (2), the scheduling algorithm relies on data products related to completeness. We estimate c by Monte Carlo experiments involving 10,000 random planets, which revolve around the star and change in brightness according to their orbital elements and the current time. Each successive search of a star harvests a different value of c equal to the number of planets not ruled out by previous searches—but detectable by this one—divided by 10,000.

Brown & Soummer (2010) develop the concept of dynamic completeness, which recognizes that the positions of all planets that were not ruled out by previous searches will continue to evolve according to their orbital elements, and possibly become observable by a future search.

c is zero immediately after an unproductive search, and so the scheduling algorithm must plan a minimum delay for the next search of this star, to allow c to recover. For habitable-zone orbits defined by equilibrium temperature, the recovery time depends on the mass and luminosity of the host star. In the current research, we pivot from Brown and Soummers results for HIP 29271, in their Figure 1, which suggests a nominal recovery time t_rcv = 58 days for that star. Our catalog values of mass and luminosity for HIP 29271 are 0.91 M_☉ and 0.83 L_☉. Therefore, our scaled estimate of the recovery time for another star, of mass M and luminosity L, is

$$\begin{equation} t_{{\rm rcv}} = 58\left({\frac{L}{{0.83}}} \right)^{3/4} \left({\frac{M}{{0.91}}} \right)^{1/2} {\rm days}{\rm.}\end{equation} \tag{ 3 }$$

Zoom In Zoom Out Reset image size

One task of the scheduling algorithm is to start the recovery clock running for any star with an unproductive search, and to bring that star back into play for selection when t_rcv has elapsed.

2.5. Planets

2.6. Input catalog of stars

We use an input catalog of 18,865 stars assigned values of L and M, distance d < 100 pc, visual magnitude V, color 0.3 ⩽ B – V ⩽ 2, and luminosity class in the range IV–V. Our sample was drawn from the NASA Star and Exoplanet Database (NStED), which has since vanished.

We assigned I magnitudes to each star using a fifth-order fit to the empirical relationship between V and I in Neill Reid's photometry at http://www.stsci.edu/~inr/phot/allphotpi.sing.2mass:

$$\begin{eqnarray} I &=& V - (1.58344 - 9.35193(B - V) \nonumber\\ &&+ 26.22379(B - V)^2 - 30.73087(B - V)^3 \nonumber\\ &&+ 16.51837(B - V)^4 - 3.20157(B - V)^5). \end{eqnarray} \tag{ 4 }$$

We remove from consideration all stars with habitable zones permanently obscured by the central field stop. The maximum possible apparent separation of a planet from its host star is

$$\begin{equation} S_{\max } = ((\alpha _{\max } = 1.5\,{\rm AU)}\;{\rm (1 + (e}_{{\rm max}} = 0.35))\,\sqrt {L/d.} \end{equation} \tag{ 5 }$$

Therefore, at the outset we can eliminate as invalid all stars for which s_max < IWA.

2.7. Overhead Time

2.8. Solar and Antisolar Avoidance

As shown in Table 1, we have adopted the values γ₁ = 45° for solar avoidance and γ₂ = 180° for antisolar avoidance (i.e., no antisolar restriction). These choices are typical of current NASA studies of similar missions.

To compute the pointing restrictions, we use a right-handed, rectangular, ecliptic coordinate system, centered on the observer, with the Sun fixed. The unit vector in the direction of the sun is always u_sun = (−1, 0, 0). We convert the right ascension and declination of the target star into ecliptic longitude Φ and latitude θ, then we convert the unit vector to the target into rectangular, ecliptic coordinates:

$$\begin{equation} {\boldsymbol u}_{{\rm target}} = \left(\begin{array}{@{}c@{}} \cos \theta \cos \left({\phi - 2\pi \frac{{t + t_{{\rm start}} - t_{{\rm ve}} }}{{365.2\,{\rm days}}} - \pi } \right), \\\ms \cos \theta \sin \left({\phi - 2\pi \frac{{t + t_{{\rm start}} - t_{{\rm ve}} }}{{365.2\,{\rm days}}} - \pi } \right), \\ \sin \theta \\ \end{array} \right), \end{equation} \tag{ 6 }$$

where t is the mission time in days, t_start is the Julian day of mission start, and t_ve is the Julian day of a vernal equinox.

The dot product of the two unit vectors is cos α = u_sun • u_target, where α is the angle between the Sun and the target as seen by the observer. The scheduling algorithm tests pointing the restriction γ₁ < α < γ₂ for candidate targets at the current mission time t.

2.9. Noise Floor

2.10. Exposure Time Calculation

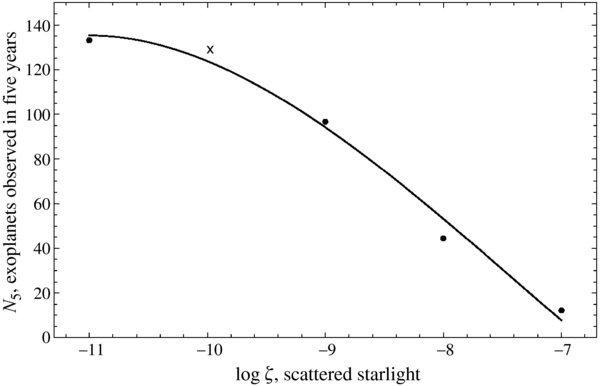
For a host star of magnitude mag_s, the exposure time τ for a planet of magnitude mag_s + Δmag is the time needed to achieve the desired signal-to-noise ratio S/N:

$$\begin{equation} {\rm S/N} = \frac{{\cal S}}{{\sqrt {{\cal S} + 2{\cal N}} }}, \end{equation} \tag{ 7 }$$

where the signal $\mathcal{S}$ is the total of planetary counts, and the noise $\mathcal{N}$ is the total of the nonplanetary counts. Both counts are gathered in the virtual photometric aperture, which comprises 1/Ψ pixels, where Ψ is the sharpness (Burrows 2003; Burrows et al. 2006). We assume "roll deconvolution," in which speckle noise is reduced by combining two statistically identical, independent images, by differencing, shifting, and adding them. The planetary image is moved a known amount between the exposures, by a small roll of telescope about the optic axis. Each exposure uses half the total exposure time. In the computer runs for this paper, we omitted the factor 2 in Equation (7). To compensate, the exposure times in Table 2, which vary as the square of S/N, should be multiplied by a factor 2 (as $\mathcal{N}$ ≫ $\mathcal{S}$). Nevertheless, because our exposure times are generally much shorter than the observational overhead, no other results or conclusions are affected.

The signal counts are

$$\begin{equation} {\cal S} = hF_{\rm p} \frac{\lambda }{{\cal R}}\frac{{\pi D^2 }}{4}\tau,\end{equation} \tag{ 8 }$$

where the planetary flux is

$$\begin{equation} F_p = F_0 \;10^{ - \frac{{{\rm mag}_s + \Delta {\rm mag}}}{{2.5}}},\end{equation} \tag{ 9 }$$

h is the end-to-end efficiency, λ is the operational wavelength, ${\cal R}$ is the spectral resolving power, D is the diameter of the aperture, and the zero point is F₀ = 4885 photons cm⁻² nm⁻¹ s⁻¹ for λ = 760 nm.

$\mathcal{N}$ is the sum of contributions from zodiacal light Z, scattered starlight ζ, dark noise υ, and read noise σ:

$$\begin{equation} {\cal N} = {\cal N}_Z + {\cal N}_\zeta + {\cal N}_\upsilon + {\cal N}_\sigma. \end{equation} \tag{ 10 }$$

We measure Z, the total zodiacal light—local plus extrasolar—in units of "zodis," the surface brightness of the local zodiacal light, mag_Z = 23 mag arcsec⁻² (Leinert et al. 1998). The counts from zodiacal light are

$$\begin{eqnarray} {\cal N}_Z &=& Z\,h\,F_0 \frac{{10^{\frac{{{\rm mag}_Z }}{{2.5}}} }}{{({4.848 \times 10^{ - 6} })^2 }}\frac{1}{\Psi }\frac{{\lambda ^2 }}{{4D^2 }}\frac{\lambda }{{\cal R}}\frac{{\pi D^2 }}{4}\tau \nonumber\\ &=& \frac{{5.271\;Z\,hF_0 \,\lambda ^3 }}{{\Psi {\cal R}}}\tau. \end{eqnarray} \tag{ 11 }$$

The counts from scattered starlight are

$$\begin{eqnarray} {\cal N}_\zeta &=& \zeta \,h\,F_0 \,10^{\frac{{{\rm mag}_s }}{{2.5}}} \frac{{\pi D^2 }}{{4\lambda ^2 }}\frac{1}{\Psi }\frac{{\lambda ^2 }}{{4\,D^2 }}\frac{\lambda }{{\cal R}}\frac{{\pi D^2 }}{4}\tau \nonumber\\ &=& \frac{{0.1542\,\zeta \,h\,F_0 \,10^{\frac{{{\rm mag}_s }}{{2.5}}} \,\lambda \,D^2 }}{{\Psi \,{\cal R}}}. \end{eqnarray} \tag{ 12 }$$

The dark and read-noise counts are

$$\begin{equation} {\cal N}_\upsilon = \frac{\upsilon }{\Psi }\tau \end{equation} \tag{ 13 }$$

and

$$\begin{equation} {\cal N}_\sigma = \frac{{\sigma ^2 }}{{\Psi \,t_r }}\tau, \end{equation} \tag{ 14 }$$

where t_r is the cadence of reading out the detector.

For the task of estimating the exposure time to achieve S/N, we can substitute it for S/N and solve the equation for τ, obtaining

$$\begin{eqnarray} \tau &=& ({\rm S/N})^2 1.121 \times 10^{ - 16 + 0.4({\rm mag}_s + \Delta\, {\rm mag} - {\rm mag}_Z)} \frac{{\cal R}}{{h\Psi D^2 F_0 }} \nonumber\\ &&\times \left(\!\begin{array}{@{}c@{}} \times 1.135 \times 10^{16 + 0.4({\rm mag}_Z)} \frac{\Psi }{\lambda } \\\ms + 1.446 \times 10^{16 + 0.40({\rm mag}_s + \Delta {\rm mag} + {\rm mag}_Z)} \frac{{2{\cal R}}}{{h\lambda ^2 D^2 F_0 }}\left({\upsilon + \frac{{\sigma ^2 }}{{t_r }}} \right) \\\ms +2.229 \times 10^{15 + 0.4(\Delta {\rm mag} + {\rm mag}_Z)} \frac{{2\;\zeta }}{\lambda } \\\ms +1.208 \times 10^{12 + 0.4(\Delta {\rm mag} + {\rm mag}_s)} \frac{{2\lambda Z}}{{D^2 }} \end{array} \!\right).\nonumber\\ && \end{eqnarray} \tag{ 15 }$$

2.11. Detector

In this section, we describe the procedure for computing a design reference mission for a given 27-vector of parameters. We use the baseline defined in Table 1 as an example.

• Step 1.  
  Restrict attention to the stars with resolved habitable zones according to s_max < IWA and Equation (5). For the baseline, some 9108 stars out of 18,865 stars in the input catalog pass this test.
• Step 2.  
  Compute an exhaustive completeness vector for each star, as follows. Generate 10,000 random planets. Test each one to find whether or not it satisfies the two criteria for detection at the current time: brightness above the noise floor (Δmag < Δmag₀) and position unobscured (s > IWA). The virgin completeness is the total number of planets satisfying these criteria divided by 10,000. Next, remove the currently detectable planets from consideration and advance the clock by a large value, say 10⁹ days. Such a long delay allows c to fully recover. Recompute c; the result is the second element in the completeness vector. Repeat these steps until all the planets ever detectable are exhausted, which is signified by a returned value of c = 0. The ith entry in the completeness vector of a star is the value of c that the scheduling algorithm will use in Equation (1) when it computes the merit function $\mathcal{Z}$ for what would be—if it is selected—the ith search of the star. The value of C to use in Equation (1) is the sum total of the first i – 1 entries in the completeness vector.The completeness vector is a random variable, which is one reason a design reference mission is a random variable. Other randomness is introduced by the scheduling algorithmdecision whether or not a planet has been detected (see Step 8 below).
• Step 3.  
  Remove all stars with a completeness vector that is identically zero, which can happen even when the habitable zone is resolved if the probability is less than 10⁻⁴ that a random planet will satisfy both detection criteria—adequate separation and brightness. This is a large effect. In a typical run with baseline parameters, only 4721 stars of the original 9108 stars remain in play after those with zero completeness are removed.
• Step 4.  
  For each star, compute the completeness recovery time t_rc and the exposure time τ_LSO from Equations (3) and (15), respectively.
• Step 5.  
  Sort the stars in descending order of $\mathcal{Z}$ as computed from Equations (1) and (2) for the first search of each star. This sorting produces atypical stack of 4721 stars, which is the starting point for building the design reference mission line by line. On top of the stack is the star with the highest merit.
• Step 6.  
  The scheduling algorithm tests the star on top of the stack for two necessary conditions: the pointing must be permitted at the current mission time t and the recovery time t_rc from any prior search must have elapsed. If these two conditions are satisfied, the star at the top of the stack is selected for the next search. If either condition is not satisfied, the scheduling algorithm moves down the stack and chooses the first star that does satisfy the two conditions. If the scheduling algorithm gets to the bottom of the stack and finds no selectable star, it advances the mission time by one day and tries again, starting at the top of the stack. The time skipped over would be available for filler observations to serve another observing program.
• Step 7.  
  The scheduling algorithm determines whether a discovery has been made by figuratively flipping a biased coin, with probability of "yes" equal to the value of $\mathcal{P}$ in Equation (1), for the values of c and C of this search.
• Step 8.  
  If "no," a discovery has not been made, then jump to Step 9. If "yes," a discovery has been made, the scheduling algorithmexecutes a series of substeps: (1) Draw one random planet for this star. If this planet is detectable at the current time by the criteria for Δmag and s, then choose this planet to be the planet found. If the planet drawn is not detectable, then try again—draw another random planet—until a detectable one is found. (2) Compute the actual exposure time for spectroscopy of this planet according to parameters 15 and 17 in Table 2. (3) Remove this star from the stack. (4) Perform the bookkeeping, which means filling out the next row in the design reference mission. (5) Advance the mission clock by the total time cost of this observation, τ_spc + t_o/h, as described in Section 2.3. (6) Loop back to Step 6 and repeat until the mission clock runs out.
• Step 9.  
  With no discovery, the scheduling algorithmperforms a different series of substeps to reinsert the star into the stack for future consideration: (1) pull up the next element in this star's completeness vector, after the one most recently used. Use this value of c—and C, the total of all prior values of c—to compute a new value of $\mathcal{Z}$ for this star. (2) Start the recovery clock running for this star. (3) Insert this star back into the stack at its new position, ranked according to its new value of $\mathcal{Z}$. (4) Advance the mission clock by the time cost of this observation, τ_LSO + t_o/h. (5) Perform the bookkeeping, creating a new row in the design reference mission. (6) Loop back to Step 6 and repeat until the mission clock runs out.

Table 11 is a snapshot of a typical design reference mission for the baseline, showing the first 10 and last 10 lines. The meanings of the 12 columns are discussed in Section 2.1. Our interest centers at first on Columns 2 and 8: the mission time t and the total number of planets observed—the science metric N. Figure 2 shows these curves for the baseline and other offsets of the major parameters, D, IWA, and t, as listed in Table 2. These results are the average of 240 design reference missions for each 27-vector. For the offsets of secondary parameters shown in Tables 4–11 and Figures 4–11, we averaged 24 design reference missions for each 27-vector.

Zoom In Zoom Out Reset image size

We see in Table 3, for the baseline 27-vector (Line 6), that 1271 stars are actually observed out of the 4721 stars in the original stack. Also, 1338 of the total 2576 observations are revisits. Also not that no filler observations were needed for the baseline.

We explore offsets from the baseline for 11 parameters: D, IWA, t, η, Z, h, ζ, Δmag₀, t_o/h, ${\cal R}$_spc, and the desired S/N_spc for spectroscopic characterization of any discovered planets.

The results for the major parameters, D, IWA, and t are summarized in Figures 1–3 and Table 3. If we regard D and IWA as independent parameters, which we do, and if typical exposure times τ are shorter than t_o/h, which they are for the baseline, then N depends only weakly on D, but strongly on IWA. The weak dependence on D is because increasing the collecting area does not significantly reduce the total time per observation, which is dominated by t_o/h.

Zoom In Zoom Out Reset image size

The two great advantages of decreasing IWA—whether D changes or not—are accessing more stars and generally increasing search completeness.

Tables 4–11 and Figures 4–11 show the parametric results for the eight secondary parameters we explore. The cases are treated as offsets from the baseline, which is why one point in the figures is always a cross, signifying the baseline case.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table 4 and Figure 4 shows that N is strictly proportional to η, which is no surprise, but good to keep in mind. We have no control over η.

Table 5 and Figure 5 show the results for zodiacal light Z. They show that N depends only weakly on Z, showing no effect for Z < 10 zodis, and only a 15%, 30%, and 40% reduction in N for Z = 50, 100, and 200 zodis, respectively. This result suggests that searching for simple infrared excesses could identify target stars with intolerable values of Z (M. Moro-Martín 2014, private communication).

Table 6 and Figure 6 show results for the end-to-end efficiency h. The time cost of an observation is τ + t_o/h. For large h, t_o/h dominates τ, and in that case improving efficiency offers little benefit in terms of the science metric N. The situation reverses for small h, when τ controls the time cost per observation, and thereby controls the total number of observations and therefore the value of N. In this regime, N depends strongly on h, and in the limit as h → 0, N → 0.

Table 7 and Figure 7 show results for scattered starlight. Decreasing ζ from 10⁻¹⁰ to 10⁻¹¹ does not increase N, but increasing it to 10⁻⁹, 10⁻⁸, or 10⁻⁷ reduces N by 30%, 65%, or 100%, respectively.

Table 8 and Figure 8 show results for observational overhead t_o/h. Reducing t_o/h from the baseline 0.5 days to 0 days increases N by 50%, while increasing t_o/h from 0.5 to 2 days reduces N by 50%. Observational overhead is important.

Table 9 and Figure 9 show results for noise floor Δmag₀. Below Δmag₀ = 26.5, decreasing Δmag₀ reduces N because the photometric completeness of all observations is reduced. Above Δmag₀ = 26.5, increasing Δmag₀ reduces N because limiting searches demand more exposure time τ_LSO to reach the lower noise floor. A science requirement on Δmag₀—which this research suggests should be Δmag₀ = 26.5—is translated by the exposure time calculator into a technical requirement on temporal stability. Because temporal stability is a complex topic involving the whole observatory—and because it is a cost driver—our results for the variation of N with Δmag₀ should be useful.

Table 10 and Figure 10 show results for spectroscopic resolving power ${\cal R}$_spc. N decreases linearly with ${\cal R}$_spc, but only weakly; if we change ${\cal R}$_spc from 17.5 to 280, N decreases by 30%. N declines as ${\cal R}$_spc increases because of the time penalty to achieve the same S/N. The reduction in N is modest because of a dilution effect: only a small fraction of all observations are affected by ${\cal R}$_spc—those producing a discovery.

Table 11 and Figure 11 show the results for the signal-to-noise of spectroscopy S/N_spc. Above the baseline value of S/N_spc, N₅ is inversely proportional to S/N_spc.

Metrical analysis of mission parameters using the formalism of the design reference mission offers insights into the basic character of missions like Terrestrial Planet Finder that search for exoplanets by direct imaging.

If search exposure times τ are short compared with observational overhead t_o/h, and if aperture D is treated as independent of inner working angle IWA, then D has a minor effect on the science metric N compared with IWA, which has a strong effect. In this regime, the benefits of reducing IWA are greater completeness and more stars with resolved habitable zones, while little benefit accrues from shortening exposure times by increasing D if t_o/h dominates τ.

Other consequences of t_o/h dominating τ include the reduced importance of end-to-end efficiency for h > 0.2, scattered starlight for ζ < 10⁻¹⁰, and zodiacal light for Z < 50 zodis.

If mission cost depends more strongly on D than on IWA, the same science may be achievable at lower cost if D and IWA can be simultaneously reduced.

The relative immunity to Z < 50 suggests that an advance survey of stars looking for infrared excesses could weed-out stars with potentially intolerable zodi. Observations with Herschel and Spitzer suggest that cold disks in outer planetary systems are common and may correlate with the occurrence of terrestrial planets and zodiacal dust in the inner planetary system (M. Moro-Martín 2014, private communication).

This research reaffirms the importance of science-operational issues in defining and optimizing missions to directly detect exoplanets (Brown et al. 2006).

I thank Stuart Shaklan for many insightful comments and questions about this research. I thank Marc Postman and Sara Seager for their encouragement. I thank Margaret Turnbull for her advice on stars. I thank Amaya Moro-Martín for sharing her views on the relationships between infrared excesses, debris disks, and exozodiacal light. I thank Sharon Toolan for her help with the manuscript.