ABSTRACT
We present an analytical study of subproton electromagnetic fluctuations in a collisionless plasma with a plasma beta of the order of unity. In the linear limit, a rigorous derivation from the kinetic equation is conducted focusing on the role and physical properties of kinetic-Alfvén and whistler waves. Then, nonlinear fluid-like equations for kinetic-Alfvén waves and whistler modes are derived, with special emphasis on the similarities and differences in the corresponding plasma dynamics. The kinetic-Alfvén modes exist in the lower-frequency region of phase space, ω ≪ k⊥vTi, where they are described by the kinetic-Alfvén system. These modes exist both below and above the ion-cyclotron frequency. The whistler modes, which are qualitatively different from the kinetic-Alfvén modes, occupy a different region of phase space, k⊥vTi ≪ ω ≪ kzvTe, and they are described by the electron magnetohydrodynamics (MHD) system or the reduced electron MHD system if the propagation is oblique. Here, kz and k⊥ are the wavenumbers along and transverse to the background magnetic field, respectively, and vTi and vTe are the ion and electron thermal velocities, respectively. The models of subproton plasma turbulence are discussed and the results of numerical simulations are presented. We also point out possible implications for solar-wind observations.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The simplest description of plasma dynamics on large scales (compared to microscales such as ion gyroradius, skin depth, etc.) is provided by one-fluid magnetohydrodynamics (MHD). In the presence of a background magnetic field, ideal MHD possesses exact nonlinear solutions—Alfvén waves propagating up and down along the magnetic field lines (e.g., Biskamp 2003; Kulsrud 2005). Interactions of counter-propagating waves redistribute energy over scales and, when the dissipation is not significant, give rise to a turbulent cascade by which energy is transferred to progressively smaller scales. It has been established that such an energy cascade is intrinsically anisotropic, in that it predominantly supplies energy to the modes with mostly field-perpendicular wavenumbers,  (e.g., Shebalin et al. 1983; Goldreich & Sridhar 1995; Galtier et al. 2000; Cho & Vishniac 2000; Boldyrev & Perez 2009; Perez & Boldyrev 2010; Perez et al. 2012).
(e.g., Shebalin et al. 1983; Goldreich & Sridhar 1995; Galtier et al. 2000; Cho & Vishniac 2000; Boldyrev & Perez 2009; Perez & Boldyrev 2010; Perez et al. 2012).
When the energy cascade reaches particle gyroscales, the one-fluid approximation breaks down and the character of the turbulence changes qualitatively. The resulting microscale plasma turbulence plays a role in laboratory experiments with strongly magnetized plasmas and it has been an important ingredient in theories of plasma confinement and magnetic reconnection (Biskamp et al. 1999; Cho & Lazarian 2004; Gürcan et al. 2009; Chandran et al. 2010; Kletzing et al. 2010). Recent high-resolution in situ observations of the solar wind also revealed the presence of significant magnetic, density, and electric fluctuations at subproton scales, often referred to as dispersion or dissipation scales, indicating a greater importance of subrange plasma dynamics in natural systems (Bale et al. 2005; Smith et al. 2006; Alexandrova et al. 2009, 2011; Kiyani et al. 2009; Sahraoui et al. 2009; Chen et al. 2010, 2012a, 2012b, 2013b; Salem et al. 2012; Šafránková et al. 2013; Podesta 2013; Kiyani et al. 2013). Studies of subproton turbulence shed light on some fundamental problems of plasma astrophysics, such as energy dissipation and particle heating by magnetic turbulence (e.g., Howes et al. 2008a; Schekochihin et al. 2009; Howes 2010; Chandran et al. 2010; Chandran 2010; Cranmer & van Ballegooijen 2012; Boldyrev & Perez 2012; Perri et al. 2012).
Microscale plasma turbulence has been studied to a much lesser extent compared with its Alfvénic counterpart. Both the qualitative nature of microscale turbulence, e.g., the plasma modes involved, the relative contributions of electrons and ions to the dynamics, and its quantitative characteristics (e.g., spectra of turbulence, degree of anisotropy, rate of energy dissipation) attract considerable interest.
Various approaches have been employed in analytical and numerical studies of plasma turbulence; these approaches have advantages or disadvantages depending on the specific goals of the study. While a full kinetic description in terms of the Vlasov–Maxwell equations is the most accurate approach, it is not practical in nonlinear numerical simulations. The gyrokinetic description provides a significant advantage over the full kinetic description in terms of computational cost, however, it is limited to frequencies below the ion-cyclotron frequency and it is not physically transparent. Fluid models are physically the most transparent and are simpler to implement in numerical simulations, however, their limits of validity are often not well established.
The two electromagnetic modes of particular interest at subproton scales are the whistler mode and the kinetic-Alfvén mode. These modes correspond to disparate regions in frequency space and they are often studied within different frameworks. In particular, the higher-frequency electron whistler modes have been discussed in the framework of the cold plasma model (e.g., Aleksandrov et al. 1984; Stix 1992) and, in the nonlinear case, in terms of electron MHD, two-fluid and Hall MHD, and shell models (e.g., Gordeev et al. 1994; Ghosh et al. 1996; Biskamp et al. 1999; Cho & Lazarian 2004; Galtier & Buchlin 2007; Shaikh & Shukla 2009; Saito et al. 2010). The lower-frequency kinetic-Alfvén modes have been discussed in kinetic, gyrokinetic, and fluid frameworks (e.g., Hollweg 1999; Howes et al. 2006; Gary & Smith 2009; Schekochihin et al. 2009; Sahraoui et al. 2012).
The subproton whistler and kinetic-Alfvén modes have characteristics in common as well as essential physical differences, which should be taken into account in phenomenological models and in the interpretation of observational data. The goal of the present work is to provide an analysis of subproton plasma turbulence, specifically concentrating on the role of kinetic-Alfvén and whistler modes. In both linear and nonlinear cases, we employ unifying analytic approaches that allow us to treat kinetic-Alfvén and whistler waves on the same footing and to effectively compare their dynamics. As subproton electromagnetic fluctuations are rarely covered in textbooks, we pay special attention to methodical aspects of the work: where possible, derivations are carried out rigorously and in detail and necessary assumptions and simplifications are clearly explained. We start with the derivation of the properties of the linear waves and then proceed with the derivation of the corresponding nonlinear equations and the analysis of the results of the numerical simulations. Our work complements previous fluid dynamics studies, gyrokinetic simulations, and known numerical solutions of the linearized Vlasov–Maxwell equations.
In the first part of this work (Sections 2–5), we present a rigorous derivation of subproton whistler and kinetic-Alfvén waves starting from the collisionless kinetic equation. We emphasize similarities and differences between these modes by establishing the sectors of the phase space where they exist, the role of the electrons and the ions in their dynamics and in their dissipation, and by analyzing the associated density fluctuations and electron and magnetic compressibilities. In the second part of the paper (Sections 6–9), we extend the analysis to the nonlinear kinetic-Alfvén and whistler dynamics. Starting from the picture of electron drift motion, in Sections 6 and 7 we derive in the equations for nonlinear kinetic-Alfvén waves in the lower-frequency region. In the higher-frequency region, we derive the equations for the whistler waves, that is, the electron MHD (EMHD) equations. We demonstrate that in the limit of strong background magnetic fields and oblique propagation, the EMHD equations simplify to the reduced EMHD (REMHD) equations; we compare and contrast the REMHD equations with the kinetic-Alfvén equations. In Sections 8 and 9, we discuss the phenomenological models of kinetic-Alfvén and whistler turbulence and present the results of numerical simulations. Finally, in Section 10, we summarize our results and discuss their relation to some other recent studies of subproton plasma turbulence.
2. METHODOLOGY
In this section, we define our notation and outline the method that we use to analyze electromagnetic subproton plasma fluctuations. We start with the collisionless kinetic equation for the distribution function of particles of sort α:
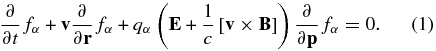
We then Fourier transform this equation in time and space and assume that the system has a uniform magnetic field B0 applied in the z-direction. We furthermore assume that the wave vector k is in the x−z plane, k = (k⊥, 0, kz). For small perturbations, the particle distribution function can be represented as fα = f0α + δfα, where f0α is a Maxwellian and δf0α is a small perturbation. The kinetic equation (1) can then be solved for the perturbation, which in cylindrical coordinates, v = (v⊥cos ϕ, v⊥sin ϕ, vz), has the form (e.g., Aleksandrov et al. 1984; Stix 1992)
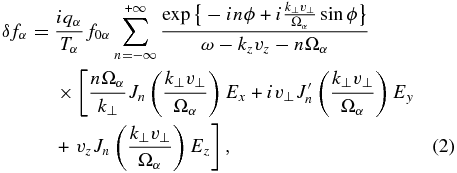
where Jn is a Bessel function of the order of n. In this expression, Ωα = qαB0/(mαc) is the gyrofrequency of the particles of sort α, which can be either positive or negative depending on the sign of the charge. Substituting Equation (2) into the Maxwell equations, one derives the dielectric tensor  ij(ω, k) in a plasma with a uniform magnetic field, whose components are given by (Aleksandrov et al. 1984)
ij(ω, k) in a plasma with a uniform magnetic field, whose components are given by (Aleksandrov et al. 1984)
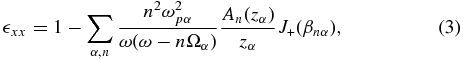
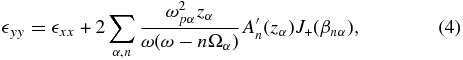
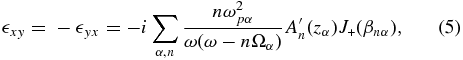
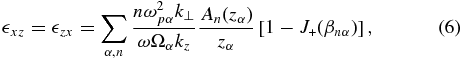
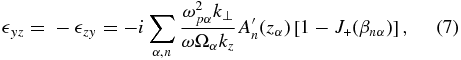
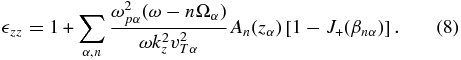
In these expressions, we used the short-hand notation
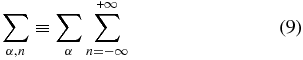
and we denoted

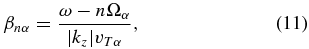

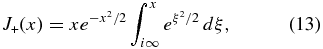
with the limiting forms
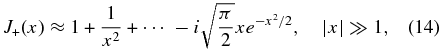
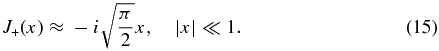
In what follows, we need to know the limiting forms of the few first functions An for zα ≪ 1, which are, to first order


The following notation is adopted here and throughout the paper:  is the plasma frequency and
is the plasma frequency and  is the thermal velocity associated with the particles of sort α. For a plasma consisting of electrons and ions, the so-called ion-acoustic velocity can be defined
is the thermal velocity associated with the particles of sort α. For a plasma consisting of electrons and ions, the so-called ion-acoustic velocity can be defined  . It is also convenient to introduce the Alfvén speed
. It is also convenient to introduce the Alfvén speed  and the plasma beta, which is the ratio of the thermal energy of the particles to the magnetic energy of the plasma. The plasma beta can be different for ions and electrons if the plasma is non-isothermal,
and the plasma beta, which is the ratio of the thermal energy of the particles to the magnetic energy of the plasma. The plasma beta can be different for ions and electrons if the plasma is non-isothermal,  ,
,  . In the above expressions, In is a modified Bessel function of the order of n and the function J+ is related to the plasma dispersion function (it should not be confused with the Bessel function).
. In the above expressions, In is a modified Bessel function of the order of n and the function J+ is related to the plasma dispersion function (it should not be confused with the Bessel function).
Our discussion is mostly motivated by astrophysical plasmas (e.g., the solar wind at 1 AU, the warm interstellar medium), where the thermal energies of particles and the magnetic field energies can be on the same order, that is, the plasma beta is of the order of 1: βα = 8πnαTα/B2 ∼ 1. Under this assumption, the particle gyroscales and the inertial scales are on the same order, that is,  . Regarding the wavelengths under consideration, we are interested in subproton but superelectron scales, that is, 1/ρi ≪ k⊥ ≪ 1/ρe. We also restrict ourselves to the frequencies below the electron cyclotron frequency, ω ≪ Ωe.
. Regarding the wavelengths under consideration, we are interested in subproton but superelectron scales, that is, 1/ρi ≪ k⊥ ≪ 1/ρe. We also restrict ourselves to the frequencies below the electron cyclotron frequency, ω ≪ Ωe.
Even within these assumptions, there are different regions that should be considered separately. To identify these regions, we first examine, in wavenumber space, the rays defined by kz = θk⊥, where θ is some constant. Then, for each such ray, we can divide the two-dimensional frequency–wavenumber space ω − k⊥ into sectors that are separated by the lines ω = kzvTe, ω = k⊥vTi, ω = Ωi, and k⊥ = 1/ρi. One can check that all the possibilities for subproton oscillations are covered by considering the regions numbered I–IV in Figures 1 and 2.
Figure 1. Asymptotic regions in ω − k⊥ space where the wave dispersion relations can be found analytically. We assume that kz = θk⊥ where θ is a constant, and that kzvTe ≫ k⊥vTi. The regions where the kinetic-Alfvén waves can exist are marked "KA"; the whistler waves can exist in the region marked "W."
Download figure:
Standard image High-resolution imageFigure 2. Asymptotic regions in ω − k⊥ space where the wave dispersion relations can be found analytically. We assume that kz = θk⊥, where θ is a constant, and that kzvTe ≪ k⊥vTi. The regions where the kinetic-Alfvén waves can exist are marked "KA."
Download figure:
Standard image High-resolution imageIn each of these regions, the wave modes can be analytically derived, if we stay sufficiently far from the boundaries. We will call those regions asymptotic regions. We will show that in asymptotic region I, the obtained dispersion relation corresponds to the kinetic-Alfvén wave. In this region, the ions are dynamically important; they are not spatially magnetized and they quickly adjust to the fluctuating electric potential. In Section 6, we demonstrate that the nonlinear dynamics in this regime can be captured by a two-field kinetic-Alfvén model, which can be used to describe the kinetic-Alfvén turbulence discussed in Section 8.
The solution in asymptotic region II corresponds to the whistler mode. The principal difference between region II and region I is the dynamics of the ions. While in the low-frequency region (region I), the ions move to adjust to the fluctuating electric potential, in the high-frequency region (region II), the ions are immobile and dynamically irrelevant. As a consequence of quasi-neutrality, the whistler waves are then not associated with plasma density fluctuations. The electron nature of waves in region II allows one to derive the nonlinear equations for the whistler waves, the so-called EMHD equations. In Section 7, we derive the EMHD equations from the electron drift picture, similar to the derivation of the kinetic-Alfvén model. We then demonstrate how the EMHD equations are simplified in the case of a strong background magnetic field and oblique wave propagation, thus leading to the REMHD model. We then compare and contrast this model with the kinetic-Alfvén model derived in Section 6. In Section 9, we discuss both weak and strong turbulence of whistlers. Finally, it can be shown that there are no solutions in regions III and IV.
In order to find the linear perturbations (waves) that can propagate in a plasma, one needs to solve the linear system of equations

where
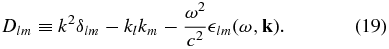
E(ω, k) is the polarization of the electric field and summation over repeated indices is assumed. In a general case, the solution of this equation cannot be obtained analytically. However, the analytic solutions can be found for the asymptotic regions I–IV in Figures 1 and 2. These solutions are derived below.
3. KINETIC-ALFVÉN WAVES
Here, we consider the solution of Equation (18) in region I, that is, we apply the assumptions ω ≪ k⊥vTi and ω ≪ kzvTe. The general expressions (3)–(8) can be simplified in this limit in the following way
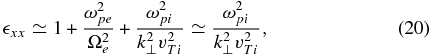


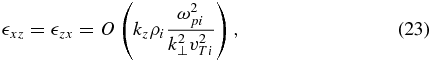
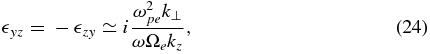

The derivation requires an explanation. While the electron contribution is derived straightforwardly from Equations (3)–(8) by keeping only the leading terms in these expressions, the ion contribution is not as easy to derive from Equations (3)–(8) since one needs to keep many similar terms in the series. For example, in the electron contribution to  xx in Equation (3), one needs to retain only the lowest-order terms n = ±1. In contrast, in the ion contribution one needs to keep the terms up to
xx in Equation (3), one needs to retain only the lowest-order terms n = ±1. In contrast, in the ion contribution one needs to keep the terms up to  , as it follows from the asymptotic form of the modified Bessel function In(z) for
, as it follows from the asymptotic form of the modified Bessel function In(z) for 
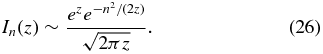
See, e.g., Abramowitz & Stegun (1972, Chapter 9) and Olver (1997). The summation over n in Equation (3) can be done with the aid of the result
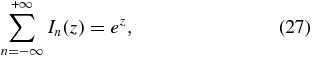
which leads to

In this derivation, we also assumed that kz ≪ k⊥, which can be verified a posteriori (cf. the discussion following Equation (40)). In a similar fashion, one can find the ion contributions to the other components of the dielectric tensor, where, together with Equation (27), one needs to use the formula
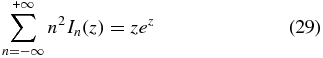
and the asymptotic result

The derivation of the ion contribution from the series in Equations (3)–(8) is however not physically transparent and it is not very convenient. A more efficient way is to note that in the limit kz ≪ k⊥, the dominant ion contribution comes through the field-perpendicular components of the ion dielectric tensor (Equations (20)–(22)). For those components, the limit of large zi corresponds to the limit of small magnetic field, in which case the ion contribution  to the dielectric tensor
to the dielectric tensor  is the same as in the non-magnetized case. Taking into account ω ≪ kvTi and kz ≪ k⊥, we have, to leading order
is the same as in the non-magnetized case. Taking into account ω ≪ kvTi and kz ≪ k⊥, we have, to leading order
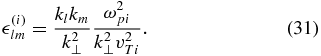
This expression for the ion contribution was used in the derivation of Equations (20)–(22). We can now write the expressions for the tensor Dlm in Equation (19)
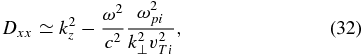

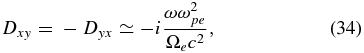

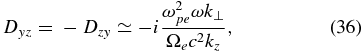
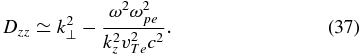
The dispersion equation (18) now allows us to write the equation for the wave frequency,  , where
, where
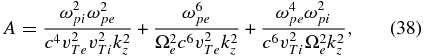

with the solution
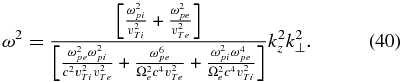
In the above expressions, we have approximated k ≈ k⊥; now, we can explain this assumption. By substituting the obtained frequency (Equation (40)) into the condition ω ≪ kvTi, we derive kzρi ≪ 1, which, together with our main assumption k⊥ρi ≫ 1, ensures that the wave propagation must be oblique. This dispersion relation can be re-written in a more familiar form by assuming singly charged ions (ni = ne) and by introducing the ion-acoustic scale ρs = vs/Ωi, where  is the ion-acoustic speed
is the ion-acoustic speed
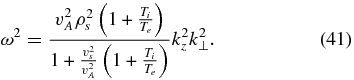
This expression is the dispersion relation for the kinetic-Alfvén waves (e.g., Camargo et al. 1996; Terry et al. 2001; Howes et al. 2006; Schekochihin et al. 2009).
For completeness, we present the polarization of the electric field, which can be found from Equation (18)

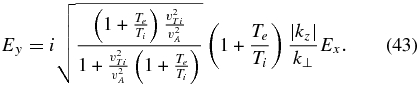
For large angles of propagation, kz ≪ k⊥, the x-component of the electric field dominates over the other two components, implying that the electric field is almost potential (e.g., Howes et al. 2006; Schekochihin et al. 2009; Sahraoui et al. 2012). We note, however, that from Equation (42) the small Ez component is not given by the potential part of the electric field (in which case we would have Ez/kz = Ex/k⊥); rather, it has comparable contributions from both the potential and the solenoidal parts. Kinetic-Alfvén waves are essentially electromagnetic, not electrostatic, waves.
We also see that the oblique kinetic-Alfvén waves are right-hand polarized, that is, their electric field rotates around the  axis similarly to the electrons. This situation is in contrast with the kinetic-Alfvén waves propagating along the guide field, which are left-hand polarized. This phenomenon, observed numerically by Gary (1986), explains why oblique kinetic-Alfvén waves do not resonate with the ions and why they can exist both below and above the ion-cyclotron frequency.
axis similarly to the electrons. This situation is in contrast with the kinetic-Alfvén waves propagating along the guide field, which are left-hand polarized. This phenomenon, observed numerically by Gary (1986), explains why oblique kinetic-Alfvén waves do not resonate with the ions and why they can exist both below and above the ion-cyclotron frequency.
Once the polarization of the electric field is obtained, the magnetic field polarization can be straightforwardly found from the induction equation, bk = (c/ω)[k × Ek]. In particular, we obtain the following expression for the amplitude of the magnetic fluctuations in kinetic-Alfvén waves

The result (Equations (42) and (43)) also allows one to analyze the electron and ion-density perturbations in the kinetic-Alfvén wave. For that, we integrate δfe in Equation (2) over velocity and obtain

where e is the modulus of the electron charge. We see that it is the z-component of the electric field that couples to the electron density, reflecting the fact that the electron motion is non-magnetized along the direction of the magnetic field.
Further insight into the physics of density fluctuations is gained if we use Equation (42) to express the electron-density perturbations through the field-perpendicular component of the electric field, Ex, which is almost potential
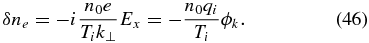
Noting that the electron and ion perturbations are the same due to quasi-neutrality, δni = δne, we observe that the ion-density perturbations follow the electric potential. This fact is not surprising if one notes that, as we discussed above, the ions are spatially non-magnetized and, therefore, their low-frequency response can be obtained from the non-magnetic collisionless kinetic equation, which leads to the result
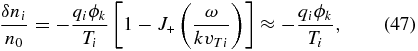
where ϕk = ik · E/k2 describes the potential part of the electric field and the asymptotic form of the function J+ is given in Equation (15). This expression is the same as Equation (46).
It may seem puzzling that the ions and the electrons follow different potentials, ϕk and  , respectively. The explanation is that the electrons are moving with a velocity ve that can be found from the integral neve = ∫vδfed3v and the magnetic field lines are advected by the same velocity. The electrons thus follow the potential ϕ' existing in the moving frame, to which they quickly adjust along the magnetic field lines. The ions, on the other hand, are not spatially magnetized and they adjust to the "laboratory-frame" potential ϕ, which is different from ϕ', since the electric field is different in different frames.
, respectively. The explanation is that the electrons are moving with a velocity ve that can be found from the integral neve = ∫vδfed3v and the magnetic field lines are advected by the same velocity. The electrons thus follow the potential ϕ' existing in the moving frame, to which they quickly adjust along the magnetic field lines. The ions, on the other hand, are not spatially magnetized and they adjust to the "laboratory-frame" potential ϕ, which is different from ϕ', since the electric field is different in different frames.
This effect reveals important differences in the electron and ion motion, which we now study in more detail. The short-cut method for calculating the electron velocity is to use the electron conductivity tensor, which is expressed through the electron part of the dielectric tensor
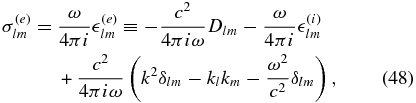
where Dlm is given by Equation (18) and  is given by Equation (31). The electron velocity is related to the electron current density,
is given by Equation (31). The electron velocity is related to the electron current density,
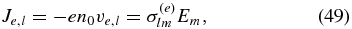
which is easy to calculate from Equation (48) since the wave electric field satisfies DlmEm = 0. As a result, we obtain the following equations for the electron velocity field

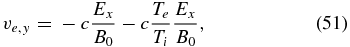
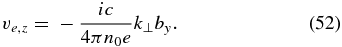
This result has the following physical interpretation. The electron-fluid velocity across the magnetic field is just the "E × B" drift plus the diamagnetic drift due to the gradient of the (isothermal) electron pressure, pe = neTe. This fact implies that the magnetic field lines are "frozen" into the electron fluid. The electron velocity along the magnetic field lines is related to the total parallel current Jz = (ic/4π)[k × b]z, since, as can be verified from Equation (48), the ion contribution to the parallel current is negligible.
The ion velocity field can be similarly calculated from the ion part of the conductivity tensor,
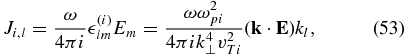
which implies that the ions, being spatially non-magnetized, adjust to the electric potential. It can be demonstrated that Equation (53) can also be obtained from the continuity equation for the ions, where the ion density is expressed through the electric potential according to Equation (47). The ions have significant velocity (comparable to that of the electrons) only in the x-direction, while their velocities in the y- and z-directions can be neglected compared with the corresponding electron velocities.
The obtained expressions also demonstrate that in the electron co-moving frame, the electric field becomes purely potential with the potential ϕ'. The electron and ion behavior that we observed in the linear case will be preserved in the case of strong kinetic-Alfvén turbulence. We will return to the fluid-like picture when we discuss the nonlinear equations for the kinetic-Alfvén waves in Section 6.
For practical applications, it may be useful to know the so-called electron compressibility, that is, the ratio of the normalized electron-density fluctuations to the normalized magnetic fluctuations (e.g., Gary & Smith 2009). From Equations (44), (46), and (42), we obtain
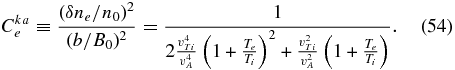
We note that this ratio is independent of wavenumber and that it strongly depends on the plasma beta  . In a similar fashion, one can obtain the so-called magnetic compressibility, that is, the ratio of the z-component of the magnetic fluctuations to the total amplitude of the fluctuations (e.g., Gary & Smith 2009). By evaluating bz from the induction equation and using Equation (44), we obtain
. In a similar fashion, one can obtain the so-called magnetic compressibility, that is, the ratio of the z-component of the magnetic fluctuations to the total amplitude of the fluctuations (e.g., Gary & Smith 2009). By evaluating bz from the induction equation and using Equation (44), we obtain
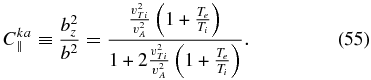
The magnetic compressibility is also independent of the wavenumber and it strongly depends on the plasma beta.
We point out that the ions are dynamically important in kinetic-Alfvén waves, which distinguishes the physics of the kinetic-Alfvén modes from the physics of the whistler modes where the ions are immobile and dynamically irrelevant. The whistler mode is discussed in the next section.
4. WHISTLER WAVES
We now consider the asymptotic region II defined by kvTi ≪ ω ≪ kzvTe. In this case, the electron contribution to the dielectric function is the same as in region I and it can be inferred from Equations (20)–(25). The ion contribution is however different, since the ions can now be treated as "cold." The ion contribution is given by

Keeping the dominant terms in the tensor Dlm, we obtain


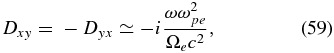
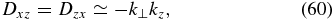
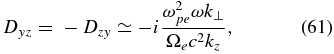
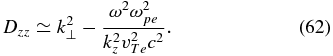
It is worth noting here that the only difference between the wave equations in the whistler and kinetic-Alfvén cases is the ion contributions in the Dxx terms in Equations (32) and (57).
The equation for the wave frequency follows from Equation (18) and it has a biquadratic form:  , where
, where

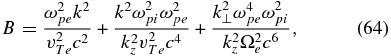

It can be checked that only one solution of this equation can be consistent with the assumption kvTi ≪ ω. For that, one has to require that kzρi ≫ 1, which implies that for the considered plasma parameters, the whistlers cannot be too oblique. In this case, the first term in Equation (64) dominates over the other two terms, C can be neglected, and a solution is found:
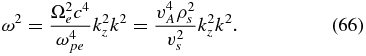
This relation is the dispersion relation for the subproton whistler waves.3 4
4
The polarization of the electric field can be found from Equation (18) in this approximation


This result, together with the fact that the electron-density fluctuations couple to the Ez-component of the electric field (see Equation (45)), implies that density fluctuations are negligible in whistler waves. This fact can be demonstrated directly from the non-magnetized collisionless kinetic equation for the ions (due to quasi-neutrality, ne = ni),

where ϕk = ik · E/k2 describes the potential part of the electric field. For high-frequency fluctuations, kvTi/ω ≪ 1, the asymptotics of the J+ function are given by Equation (14), which shows that the density variations are indeed negligibly small,
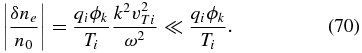
In particular, one can compare the density fluctuations to the magnetic fluctuations by calculating the electron compressibility, similarly to our discussion in Equation (54). From the magnetic induction equation and the electric field polarization (Equations (67) and (68)), we obtain the magnetic field fluctuations in the whistler wave,

and the electron compressibility for the whistler wave is found to be

Therefore, the whistler electron compressibility is small, as whistlers exist only for kz > 1/ρi ∼ ωpi/c. Our analytic result explains the behavior previously observed numerically by Gary & Smith (2009); moreover, it turns out that Equation (72) formally derived in the asymptotic limit (ωpi/(kzc) ≪ 1) holds quite well already for ωpi/(kzc) ≲ 1.
In addition, the properties of the whistler waves can be characterized by the magnetic compressibility, which is defined as
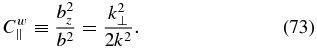
The whistler magnetic compressibility is independent of the plasma beta, and it is practically independent of wavenumber for kz ≪ k⊥.
The obtained results reveal essential differences between the kinetic-Alfvén modes and the whistler modes. The kinetic-Alfvén modes are compressible modes where the ion dynamics play an essential role. For the considered plasma parameters, they exist at the subproton scales in the frequency range ω ≪ kvTi, kzvTe (depicted as region I in Figures 1 and 2) and in the wavenumber range kzρi ≪ 1. In contrast, the whistler waves are electron waves, where the ion dynamics are not essential. The ions provide a uniform stationary background, which, together with the quasi-neutrality condition, explains the incompressible character of whistler waves. We note that it is the high frequency of the whistler waves, not the large plasma beta, that ensures the immobility of the ions and the resulting incompressibility of the whistler modes. For the considered plasma parameters, the whistler waves exist at subproton scales in the frequency range kvTi ≪ ω ≪ kzvTe (depicted as region II in Figure 1) and in the wavenumber range kzρi ≫ 1.
Therefore, the kinetic-Alfvén modes and the whistler modes correspond to different frequency and wavenumber ranges and they are governed by different physical mechanisms. This fact is reflected in, e.g., the different normalizations of the dispersion relations, (cf. Equations (41) and (66)) and the different variation of electron and magnetic compressibilities with plasma parameters (cf. Equations (54) and (55) with Equations (72) and (73)). Finally, it can be checked that under the considered plasma parameters, there are no wave modes in regions III and IV.
5. COLLISIONLESS DISSIPATION OF KINETIC-ALFVÉN AND WHISTLER WAVES
So far, we considered the subproton plasma fluctuations under the assumption that dissipation can be neglected. In this section, we evaluate the damping of subproton fluctuations due to weak collisionless dissipation. The terms responsible for the dissipation in the dielectric tensor (Equations (3)–(8)) arise from the small imaginary parts of the function J+ in Equations (14) and (15), which should now be retained together with the real parts. As a result, the components of the dielectric tensor will acquire small corrections,  , and the corresponding small corrections will appear in the tensor
, and the corresponding small corrections will appear in the tensor  , where
, where  and the superscript 0 denotes the components where the dissipation parts are neglected.
and the superscript 0 denotes the components where the dissipation parts are neglected.
The solution of the new dispersion equation  will now take the form ω = ω0 + iγ, where ω0 is the frequency of a non-dissipative wave, and γ is the small dissipation rate. Owing to the smallness of δ
will now take the form ω = ω0 + iγ, where ω0 is the frequency of a non-dissipative wave, and γ is the small dissipation rate. Owing to the smallness of δ lm and γ, the dispersion equation can be re-written in a simplified form. Let us denote
lm and γ, the dispersion equation can be re-written in a simplified form. Let us denote  and Mlm as the cofactor corresponding to the matrix element Dlm. We then have
and Mlm as the cofactor corresponding to the matrix element Dlm. We then have
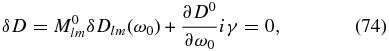
where we used the identity ∂D/∂Dlm = Mlm and summation over repeated indices is assumed. We therefore derive the general expression for the dissipation rate
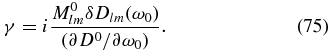
Further simplification comes from the observation that in both the kinetic-Alfvén case and the whistler case, the determinant has a simple general form,
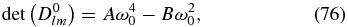
which leads to ∂D0/∂ω0 = 2Bω0. The coefficient B for the kinetic-Alfvén case is found in Equation (39); for the whistler case, B is found in Equation (64).
We now consider the dissipation separately for the kinetic-Alfvén waves and the whistler waves. In the case of βi ∼ 1, the dissipation of oblique kinetic-Alfvén waves is dominated by the electron contribution, see, e.g., the numerical solutions of the Vlasov–Maxwell equations in Howes et al. (2008a). We will therefore consider only electron dissipation in this case. In contrast, in the case of the whistler waves, ion dissipation becomes significant and it may quickly overcome the electron dissipation as the obliquity increases. In the whistler case, we therefore derive both electron and ion contributions to the dissipation.
In the kinetic-Alfvén case, the dominant dissipation terms in the tensor Dlm are
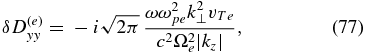
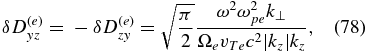
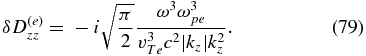
A straightforward but somewhat lengthy calculation using Equation (75) then gives

where

where we denoted a = Te/Ti. Formulae (80) and (81) describe the collisionless damping of the subproton kinetic-Alfvén waves; they agree with previous findings (e.g., Howes et al. 2006, 2008b). For the case of βi = 1 and a = 1, we estimate  .
.
We now turn to the discussion of collisionless damping of whistler waves. The dissipative contributions to the Dlm tensor will now be given by both the electrons and the ions. The electron contribution is given by the same expressions (77)–(79) as in the kinetic-Alfvén case. The ion contribution is obtained from the dielectric tensor for non-magnetized ions. Taking into account that whistlers exist in the region ω ≫ kvTi, we obtain
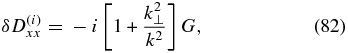

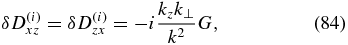
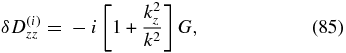
where we have denoted
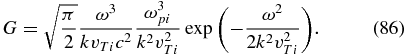
A straightforward computation taking into account both electron and ion contributions leads to the dissipation rate of the subproton whistler waves:
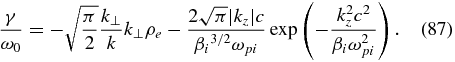
We see that the electron dissipation of the whistler waves (the first term in Equation (87)) is comparable to that of the kinetic-Alfvén waves, while the ion contribution to the dissipation (the second term in Equation (87)) may become significantly larger when the propagation is oblique. For example, for βi = 1, the ion dissipation rate is about 1.6% for kzc/ωpi = 2.5 and it reaches 14% for kzc/ωpi = 2. Thus, the ion dissipation rate increases quickly as kzc/ωpi decreases so that the whistlers become strongly damped by the ions at kzc/ωpi ≲ 2.
From Equation (87), it follows that the electron damping of whistlers limits k⊥ from above while the ion damping limits kz from below, imposing restrictions on the obliquity of propagation. For a given k⊥, as kz decreases and the propagation becomes more oblique, the dissipation becomes stronger and the whistler wave ceases to exist at kz ∼ ωpi/c. It is easy to see that this boundary corresponds to the line ω = k⊥vTi in Figure 1, separating the whistler region II from the kinetic-Alfvén region I in phase space. For even more oblique propagation (below the boundary ω = k⊥vTi), a new mode appears in region I, the kinetic-Alfvén wave, whose dispersion relation is different from that of a whistler wave.
The discontinuity between the dispersion relations of the kinetic-Alfvén and whistler waves, Equations (41) and (66), reflects the differences in the physics governing the two modes. These differences must be taken into account in order to derive the nonlinear equations for the whistler and kinetic-Alfvén waves. This analysis is presented in the following sections. We demonstrate that the whistler waves are described by the EMHD equations or, in the case of oblique propagation, by the REMHD equations. In contrast, the kinetic-Alfvén waves are described by the kinetic-Alfvén system of equations, which is different from the EMHD equations.
6. NONLINEAR KINETIC-ALFVÉN EQUATIONS
As we discussed in Section 3, kinetic-Alfvén waves exist in the wavenumber region kz ≪ k⊥ for the plasma parameters we consider, where kz and k⊥ are the typical wavenumbers of fluctuations in the directions parallel and perpendicular to the magnetic field, respectively. As will be explained in more detail below, the nonlinear effects in this case become significant for relatively small fluctuations of the magnetic field, satisfying kzB0 ∼ k⊥b, where B0 is the non-fluctuating component and b is the fluctuating part of the magnetic field. This fact implies that even in the case of strong turbulence, fluctuations of the distribution function remain small and they can be obtained through perturbation theory.
To demonstrate this finding, we consider the electron kinetic equation (Equation (1)) with a small electric field. This equation has a solution of the form fe(x, v, t) ≃ f0e(v) + δfe, where f0e is Maxwellian5 and the small perturbation δfe is given by Equation (2). From this expression, we estimate δfe ∼ (eϕ'/T)f0e, where we denote ϕ' = iEz/kz. The applicability of the perturbation procedure thus requires that eϕ'/T ≪ 1. This condition does not necessarily imply that the corresponding turbulence is weak, however. Indeed, the condition for strong turbulence, k⊥b ∼ kzB0, implies that eϕ'/T ∼ kz/k⊥ ≪ 1. Thus, the perturbation expansion holds even in the case of strong turbulence if the wave propagation is oblique (e.g., Howes et al. 2008a). The same conclusion could also be reached starting from the ion kinetic equation, with the quasi-neutrality condition ensuring that qiϕ/Ti ∼ −eϕ'/Te ≪ 1.
In order to derive fluid-like equations for nonlinear kinetic-Alfvén waves, we now consider the first two moments of the electron kinetic equation (Equation (1)). First, we integrate this equation over velocity and obtain the electron continuity equation
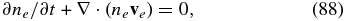
where, by definition, ne = ∫fed3v and neve = ∫fevd3v. Second, we multiply the equation by v and integrate over velocity to obtain the momentum equation
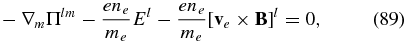
where Πlm = ∫vlvmfed3v, summation over repeated indices is assumed, and we neglected the time derivative (or the electron inertia term) since we are interested in low-frequency fluctuations, ω ≪ kzvTe.
To calculate the term Πlm in the resulting force-balance equation, we need to know the electron distribution function. In principle, the electron distribution function can be calculated from the kinetic equation perturbatively assuming a small parameter eϕ'/Te. However, the form of the distribution function can be established in a simpler way if we use the conditions ω ≪ kzvTe and k⊥ρe ≪ 1. The first condition tells us that we can neglect the term ∂fe/∂t in the kinetic equation. The second condition allows us to look for the solution of the form (Aleksandrov et al. 1984)
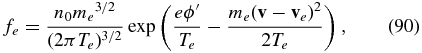
where Te = const and the electron drift velocity ve is much smaller than the electron thermal velocity. The functions ϕ'(x, t) and ve(x, t) are related to the electric and magnetic fields through

The solution (Equation (90)) approaches the Maxwellian distribution for eϕ'/Te → 0.6 Equation (91) explains the fact already observed in the linear case that the electrons adjust to the potential existing in the co-moving frame. We now obtain from Equation (90) the pressure tensor in the form:

where
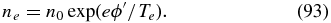
With the aid of Equations (88) and (92), the force balance in the electron momentum equation can be re-written in a fluid-like form
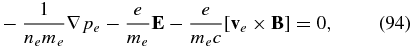
where pe = neTe is the electron pressure. The force-balance equation thus agrees with that of an isothermal electron fluid.
Analogously, in the low-frequency regime, ω ≪ k⊥vTi, the solution for the ion kinetic equation is expected to have the form
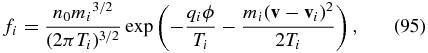
where Ti = const and vi is much smaller than the ion thermal speed. Similarly to the electron case, the potential ϕ and the ion drift velocity satisfy the equation
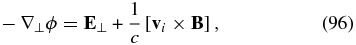
although in the ion case this equation holds only for the component of the electric field perpendicular to the magnetic field, since the ion motion along the field lines may not satisfy the low-frequency condition  . It can be checked that due to k⊥ρi ≫ 1, the last term in Equation (96) must be small7 and we can approximate −∇⊥ϕ ≈ E⊥. Noting that in the case of
. It can be checked that due to k⊥ρi ≫ 1, the last term in Equation (96) must be small7 and we can approximate −∇⊥ϕ ≈ E⊥. Noting that in the case of  the perpendicular component of the electric field dominates,
the perpendicular component of the electric field dominates,  , we see that ϕ represents the potential part of the electric field. Similarly to the derivation of Equation (94), we now integrate the ion kinetic equation with v and derive the part perpendicular to the magnetic field
, we see that ϕ represents the potential part of the electric field. Similarly to the derivation of Equation (94), we now integrate the ion kinetic equation with v and derive the part perpendicular to the magnetic field
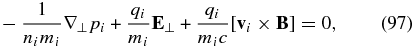
where
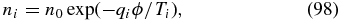
and pi = niTi is the ion pressure. Equation (97) can be used to remove the electric field from the electron force-balance equation (Equation (94)), which allows us to re-write its part perpendicular to the magnetic field in a more familiar fluid-like form
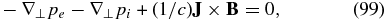
Equations (88), (94), and (97), along with the magnetic induction equation, form a complete set of equations for kinetic-Alfvén waves.
We represent the magnetic field in terms of the mean and fluctuating parts as follows  . The fact that the z-component of the magnetic fluctuations should be retained, together with B0, follows from the force-balance equation (Equation (99)). Taking into account
. The fact that the z-component of the magnetic fluctuations should be retained, together with B0, follows from the force-balance equation (Equation (99)). Taking into account  , we derive from this relation
, we derive from this relation
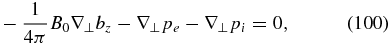
which gives an estimate bz/B0 ∼ β(δne/n0). For β ≪ 1, the fluctuations of bz can be neglected, while for β ∼ 1 (the case we consider in this work) they should be retained.
From the force balance in the electron momentum equation (Equation (94)), it follows that the electrons are advected across the magnetic field by the "E × B" drift velocity and the diamagnetic drift velocity, respectively,
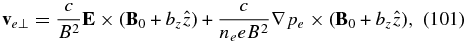
where an approximate expression  should be substituted in the denominators of Equation (101). As for the motion of the electrons parallel to the magnetic field it can be expressed through the current
should be substituted in the denominators of Equation (101). As for the motion of the electrons parallel to the magnetic field it can be expressed through the current  , since the velocity of ions parallel to the field is relatively small. The perpendicular component of the fluctuating magnetic field can be expressed through the flux function
, since the velocity of ions parallel to the field is relatively small. The perpendicular component of the fluctuating magnetic field can be expressed through the flux function  , such that
, such that

The flux function is the (negative) component of the vector potential parallel to the field, ψ = −Az. In the considered case of strong anisotropy,  , the component of the fluctuating magnetic field parallel to the field is related to the (non-potential) component of the electric field perpendicular to the field through the magnetic induction equation,
, the component of the fluctuating magnetic field parallel to the field is related to the (non-potential) component of the electric field perpendicular to the field through the magnetic induction equation,
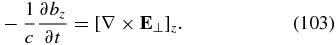
To derive the equations for nonlinear kinetic-Alfvén waves, we use the electron continuity equation (Equation (88)) and the magnetic induction equation. The force balance parallel to the magnetic field in the electron momentum equation (Equation (94)) gives
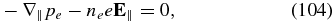
where the electric field is E = −∇ϕ − (1/c)∂tA. Supplementing this equation with the electron continuity equation,
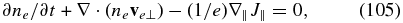
and using the induction equation (Equation (103)) to express the non-potential part of the electric field, one obtains the following system of equations for the fluctuating parts of the magnetic and density fields:
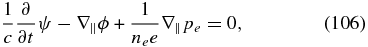

These equations are written in general form, where the pressure term for the electrons can be arbitrary as long as the fluid description of Equations (88) and (94) holds. Such equations were derived and studied previously in various regimes, (e.g., Hazeltine 1983; Scott et al. 1985; Camargo et al. 1996; Terry et al. 2001; Schekochihin et al. 2009; Smith & Terry 2011; Boldyrev & Perez 2012). In the case relevant to our consideration, the equations of state are isothermal.
In the nonlinear case when the magnetic fluctuations obey kzB0 ∼ k⊥b, we must distinguish the gradients along the guide field B0, denoted as ∇z, from the gradients along the local field B = B0 + b, denoted as  . The gradients in Equations (106) and (107) parallel to the field are thus defined as
. The gradients in Equations (106) and (107) parallel to the field are thus defined as
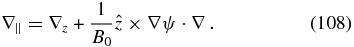
In our discussion of strong kinetic-Alfvén turbulence, we will assume that the fluctuations are anisotropic with respect to the magnetic field in such a way that the linear and nonlinear terms in Equations (107) and (110) are of the same order, that is,
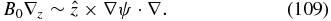
This ordering is analogous to the so-called critical balance condition, kzB0 ∼ k⊥b, of Goldreich & Sridhar (1995); see also Cho & Lazarian (2004), Howes et al. (2011), and TenBarge & Howes (2012). This ordering shows that for kz ≪ k⊥, nonlinearity becomes important already for small perturbations. When condition (109) is satisfied, Equations (106) and (107) are essentially nonlinear and three-dimensional.
For completeness, we also note that in the limit of small plasma beta, we have bz → 0 and the electron continuity equation (107) turns into
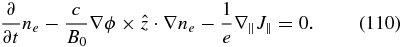
This equation demonstrates that in the limit of small beta the electrons are advected across the field lines only by the "E × B" drift. Indeed, when the magnetic field strength does not change, that is, bz = 0, the diamagnetic drift does not advect the electron density. Physically, this situation occurs because the guide centers of particles do not move when a diamagnetic current is present. That is why the diamagnetic drift does not enter Equation (110) even in the case of a general equation of state. However, if the magnetic field strength changes, the magnetic curvature effects do affect the density advection and terms with derivatives of bz do not cancel out.
The system of equations involving three fields, ne, ψ, and ϕ ((106) and (110)) or the system of equations involving four fields ne, bz, ψ, and ϕ ((106) and (107)) are incomplete, as they have more independent fields than equations. The uniqueness is restored when the systems are supplemented by the equations for the ions. The situation here depends on the scales considered. Briefly deviating from our main discussion, we mention that above the ion-cyclotron scale, ρi = vTi/Ωi, a fluid description can be justified for the ions if the ions are cold, which is essentially the limit of low beta. (This case is applicable to most laboratory plasmas, the context in which the corresponding equations were originally derived.) In this case, the ions move across the magnetic field due to the "E × B" drift and the so-called polarization drift. One can write the charge conservation law,  , where the parallel current is given by the electrons, while the perpendicular current is due to the polarization drift of the ions (the "E × B" drifts are the same for ions and electrons; they do not lead to charge separation and do not contribute to the current). It can be shown that quasi-neutrality is preserved for ωpα ≫ Ωα, therefore, the charge continuity equation can be reduced to
, where the parallel current is given by the electrons, while the perpendicular current is due to the polarization drift of the ions (the "E × B" drifts are the same for ions and electrons; they do not lead to charge separation and do not contribute to the current). It can be shown that quasi-neutrality is preserved for ωpα ≫ Ωα, therefore, the charge continuity equation can be reduced to  , which can be re-written as (e.g., Terry et al. 2001)
, which can be re-written as (e.g., Terry et al. 2001)
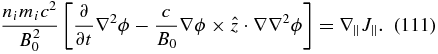
Equations (106), (110), and (111) provide the closed three-field system for evolution of electric, magnetic, and density fields in the case of low plasma beta.
If the plasma beta is not small (the case of interest in this work), the ions require kinetic description and a simple fluid model is not justified. We, however, are interested in the subproton, dispersive kinetic-Alfvén waves, that is, we consider scales smaller than the ion gyroscale k⊥ρi ≫ 1. At such scales, the ions are (spatially) not magnetized. Moreover, since we are interested in frequencies smaller than kvTi, we have the simple response for the ion-density fluctuations (Equations (98) and (69)). The quasi-neutrality condition ni = ne then relates the electric potential to the electron density,
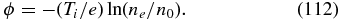
Similarly, in the three-field system, the bz field can be removed from Equation (107) with the aid of the force-balance equation perpendicular to the magnetic field (Equation (100)):
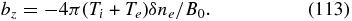
These expressions for the electric potential ϕ and the magnetic field bz leave us with only two independent fields, the electron density and the magnetic flux function. Let us normalize these expressions as follows
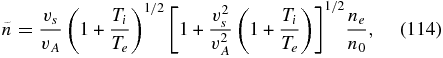

and normalize the time and the length according to
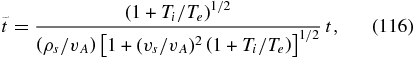

In the rest of this section, we will use only the normalized variables and we will omit tilde symbol. The system (Equations (106) and (107)) then takes the form


where  . Notice that the nonlinearity enters this system only through the magnetic-line bending effects in
. Notice that the nonlinearity enters this system only through the magnetic-line bending effects in  .
.
The presented ideal system conserves total energy E and the cross-correlation H:
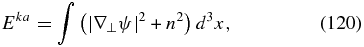

The system (Equations (118) and (119)) possesses linear waves, nk∝ψk∝exp (− iωt + ikx). The linearization is achieved by neglecting the second term in the right-hand side of Equation (108), that is, by replacing ∇|| → ∇z, which gives the (dimensionless) dispersion relation for the kinetic-Alfvén waves:

The linear modes are characterized by the equipartition between the density and magnetic fluctuations, nk = ±k⊥ψk.
It is easy to check that the linearized equations produce the same dispersion relation and wave polarization given by the kinetic theory, that is, Equations (41)–(43). Also, note that we do not require the frequencies to be smaller than the ion gyrofrequency, as is implied, e.g., in gyrokinetic treatments, therefore, our results are applicable to region I in Figures 1 and 2 both below and above Ωi.
7. NONLINEAR WHISTLER EQUATIONS: ELECTRON MHD AND REDUCED ELECTRON MHD
As we demonstrated in Section 4, for the considered plasma parameters the whistler waves exist only in the wavenumber region kz/k⊥ ≫ 1/(k⊥ρi), which implies that kz cannot be too small compared with k⊥. According to the critical balance condition (Equation (109)), the nonlinear effects become important for the whistler waves for magnetic field fluctuations that are significantly larger compared with those in the kinetic-Alfvén case. It is therefore reasonable to expect that whistler turbulence, if it is present in those systems at subproton scales, should predominantly be weak. In this case, the kinetic treatment presented in Section 4 should suffice.
If, however, nonlinearities need to be taken into account, it is convenient to use a nonlinear system for whistler waves. This system is derived if one notes that the frequencies of whistler modes are high, ω ≫ kvTi, so that the ions can be considered cold. Moreover, since we are studying subproton scales, k⊥ρi ≫ 1, the ions are non-magnetized both spatially and temporally, ω ≫ Ωi. The fluid equations for "cold" non-magnetized ions then agree with the single-particle motion equations,
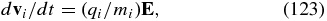
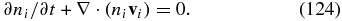
For the density fluctuations, these equations lead to exactly the same expression as Equation (70), which demonstrates that for high frequencies, ω ≫ kvTi, the ion-density fluctuations can be neglected. The ion fluctuation velocity is estimated from these equations as vi ∼ (qϕ/Ti)(kvTi/ω)vTi, while the electron velocity is estimated from the current to be ve ∼ J/(ne) ∼ ckB/(ne). We therefore obtain that the ion velocity is negligible compared with the electron velocity,
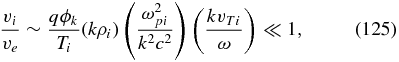
where we used kρi ∼ kc/ωpi ≫ 1 and kvTi/ω ≪ 1.
Similar to the kinetic-Alfvén case, we now use the force balance in the electron momentum equation (Equation (94)) and the magnetic induction equation. The force balance is easy to write if one neglects the pressure-gradient term (indeed, the electrons are isothermal and their density does not change)
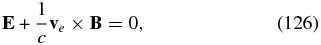
where ve = −J/(n0e). The induction equation then takes the form
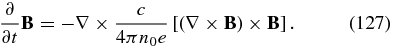
This equation is the electron MHD (EMHD) equation (e.g., Gordeev et al. 1994). A linearization of Equation (127) around a uniform background field B0 leads to the dispersion relation of whistler waves (Equation (66)).
We now demonstrate how the EMHD equations can be simplified in the presence of a uniform magnetic field B0 and anisotropic fluctuations, kz/k⊥ ≪ 1. In the case of oblique propagation, the system becomes strongly nonlinear for a relatively small fluctuating field, satisfying the critical balance condition b/B0 ∼ kz/k⊥. The EMHD equation (Equation (127)) can then be simplified by keeping only the leading terms in this small parameter (c.f., e.g., Schekochihin et al. 2009). As a result, one obtains what we call the reduced electron MHD (REMHD) equations, which can be conveniently written in terms of the two variables, the z-component of the magnetic field, bz, and the z-component of the vector potential, ψ = −Az:


with the same definition of  as in Equation (108).
as in Equation (108).
To elucidate the similarities and differences between the REMHD equations (Equations (128) and (129)) and the previously derived kinetic-Alfvén equations (Equations (118) and (119)), it is instructive to also derive the REMHD equations directly from the electron drift picture, similar to our derivation of the kinetic-Alfvén system (Equations (106) and (107)). For that, we first analyze the force balance in the electron momentum equation. When the electron-density fluctuations are neglected, this equation takes the form of Equation (126). For the considered case of oblique propagation satisfying the critical balance condition, we obtain the following equation for the component perpendicular to the magnetic field
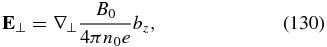
which demonstrates that the perpendicular component of the electric field is almost potential, that is, E⊥ = −∇⊥ϕ, where

This result is also consistent with the linear case, where the whistler electric field is given by Equations (67) and (68), and it becomes almost potential for kz ≪ k⊥.
Substituting the expression for the electric potential (Equation (131)) into Equations (106) and (107) and neglecting the electron-density fluctuations, we rederive the REMHD equations (Equations (128) and (129)). Note the essential difference in the expressions for the electric potential and the electron density used in the derivation of the REMHD equations (Equation (131) and δne ≈ 0) and the corresponding expressions used in the derivation of the kinetic-Alfvén equations (Equations (112) and (113)). These differences reflect the different dynamics of the ions in the two systems.
Similarly to the kinetic-Alfvén case, one can introduce the dimensionless variables
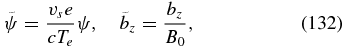
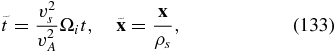
which cast the REMHD system (Equations (128) and (129)) into the form

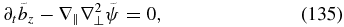
which is structurally equivalent to the kinetic-Alfvén system (Equations (118) and (119)). The corresponding conservation laws are now the conservation of energy and helicity of the magnetic fluctuations
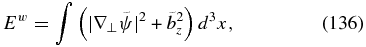

Although the mathematical structure of the obtained system is formally equivalent to that of the kinetic-Alfvén system, the normalization of the fields (Equations (132) and (134)) is different owing to the difference in the ion dynamics between the two systems. The mathematical similarity of the REMHD system and the kinetic-Alfvén system, however, implies similarity in the scaling relations of the corresponding turbulent states, which are discussed in the following sections.
Before we leave the discussion of the nonlinear equations, we note that the considered subproton kinetic-Alfvén and EMHD equations provide examples of systems where a fluid description can be applied to a collisionless, or weakly collisional, plasma. The applicability of the fluid approximation to collisionless plasmas in certain cases is a known fact; other examples and further discussion can be found in, e.g., Ginzburg (1970) and Aleksandrov et al. (1984).
8. KINETIC-ALFVÉN TURBULENCE
In a turbulent state, the energy E cascades toward small scales while the cross-correlation H cascades toward large scales. A standard phenomenological approach addressing the energy cascade at small scales is discussed in, e.g., Vainshtein (1973), Biskamp et al. (1999), Ng et al. (2003), Cho & Lazarian (2004), Howes et al. (2008b) and Cho & Lazarian (2009). This approach assumes that in strong turbulence the critical balance condition, which ensures that both linear and nonlinear terms in Equation (108) are of the same order, should be satisfied at all scales. Let us denote nλ and ψλ the typical (rms) fluctuations of the density and the magnetic flux function, respectively, at the field-perpendicular scale λ, and l as the corresponding scale of those fluctuations parallel to the field. By balancing the linear and nonlinear terms in Equation (108), we estimate l ∼ λ2/ψλ, in which case the time of nonlinear interaction is comparable to the inverse of the linear frequency (Equation (41)), τ ∼ 1/ω ∼ lλ ∼ λ3/ψλ. In addition, we estimate from Equations (118) and (119) that nλ ∼ ψλ/λ. The energy associated with the scale λ can therefore be estimated as  , and the condition of constant energy flux in the turbulent cascade leads to
, and the condition of constant energy flux in the turbulent cascade leads to  , which translates into a scaling of nλ ∼ ψλ/λ ∼ λ2/3 for turbulent fields. The resulting Fourier energy spectrum of strong kinetic-Alfvén turbulence is
, which translates into a scaling of nλ ∼ ψλ/λ ∼ λ2/3 for turbulent fields. The resulting Fourier energy spectrum of strong kinetic-Alfvén turbulence is
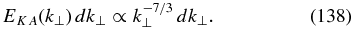
We will numerically study kinetic-Alfvén turbulence based on the dimensionless equations (118) and (119). As was previously explained, the critical balance condition requires that kz ≪ k⊥ in the case of strong turbulence. We note, however, that the ideal equations (118) and (119) admit a rescaling ∂/∂t →  ∂/∂t, ∇z →
∂/∂t, ∇z →  ∇z, n →
∇z, n →  n, and ψ →
n, and ψ →  ψ with arbitrary
ψ with arbitrary  , which preserves the critical balance. This result reflects the fact that equations (118) and (119) lack any frequency scale, since they are derived in the limit of an infinitely large electron gyrofrequency. We may therefore always simultaneously rescale the fields in these equations and the size of the simulation box in the z-direction to satisfy kz ∼ n ∼ ψ ∼ 1. Such a rescaling is assumed in the numerical simulations discussed below.
, which preserves the critical balance. This result reflects the fact that equations (118) and (119) lack any frequency scale, since they are derived in the limit of an infinitely large electron gyrofrequency. We may therefore always simultaneously rescale the fields in these equations and the size of the simulation box in the z-direction to satisfy kz ∼ n ∼ ψ ∼ 1. Such a rescaling is assumed in the numerical simulations discussed below.
To study steady-state turbulence, we supplement Equations (118) and (119) with large-scale random forces that supply the energy to the system:
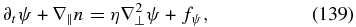
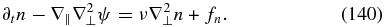
The small dissipation terms serve to remove energy at small scales and they are mostly needed to stabilize the code. We solve these equations on a triply periodic cubic domain (L3, L = 1) using standard pseudo-spectral methods. The random forces fψ and fn are applied in Fourier space at wavenumbers 2π/L ⩽ kx, y ⩽ 2(2π/L), kz = 2π/L. The Fourier coefficients outside the above range are zero and are Gaussian random numbers with amplitudes chosen so that |∇ψ|rms ∼ 1 inside that range. The individual random values are refreshed independently on average every τ = 0.1L/(2π|∇ψ|rms). We choose ν = η = 0.01.
The energy spectrum obtained numerically is shown in Figure 3. It turns out that it is steeper than the spectrum −7/3 predicted by phenomenological theories based on dimensional arguments. It is interesting that a spectrum steeper than −7/3 was also inferred from observations of subproton magnetic and density fluctuations in the solar wind (e.g., Sahraoui et al. 2006; Chen et al. 2010, 2012b; Alexandrova et al. 2011, 2012).
Figure 3. Energy spectrum of strong kinetic-Alfvén turbulence at subproton scales, obtained in two-field numerical simulations with a resolution a 5123 (Boldyrev & Perez 2012) and compensated by k8/3. For comparison, the dash-triple-dot line shows the total spectrum compensated by k7/3. k⊥ is plotted on the horizontal axis.
Download figure:
Standard image High-resolution imageVarious explanations have been proposed for the steeper than −7/3 spectrum of subproton turbulence observed in the solar wind. These explanations include steepening of the spectrum by Landau damping, turbulence weakening, wave–particle interactions, etc. (e.g., Rudakov et al. 2011; Howes et al. 2011). In our analytical and numerical approach, wave–particle interactions are absent, however, the steeper spectrum persists. A possible explanation proposed in Boldyrev & Perez (2012) invoked intermittent corrections that result from two-dimensional structures formed by density and magnetic fluctuations. It was proposed that the spectrum should be close to −8/3, a value consistent with observations and numerical simulations. This fact points to an interesting possibility that the observed scaling is not an artifact of non-universal or dissipative effects; rather, it is an inherent property of the nonlinear turbulent dynamics. The spectrum may therefore be universal, analogous to the Kolmogorov spectrum of fluid turbulence. A definitive numerical study that requires higher numerical resolution will be conducted elsewhere.
We also note that the magnetic energy exceeds the kinetic energy at all scales in the inertial interval. Quite interestingly, the ratio of the density energy to the magnetic energy, the nonlinear electron compressibility, is independent of the wavenumber in the inertial interval, which is similar to the behavior observed in the linear case (cf. Equation (54)). Our additional runs (not shown here) demonstrate that the excess of the magnetic energy is not related to the forcing routine; the excess of magnetic energy in the inertial interval is also observed in simulations where only the density field is forced or where both the density and magnetic fields are forced at large scales. From Figure 3 we estimate |bk⊥|2/|nk|2 ≈ 1.25 in dimensionless units (Equations (114)–(117)).8 We propose that this effect is analogous to the generation of residual energy in MHD turbulence, where magnetic energy also provides the dominant contribution (e.g., Frisch et al. 1975; Müller & Grappin 2005; Podesta et al. 2007; Tessein et al. 2009; Mininni & Pouquet 2009; Boldyrev & Perez 2009; Wang et al. 2011; Boldyrev et al. 2011, 2012; Borovsky 2012; Chen et al. 2013a). We also point out that it is the total energy rather than its density and magnetic field components that exhibits a good scaling in an interval of limited extent, in close analogy with MHD turbulence.
Finally, we discuss the spectrum of the electric field. In our model, its potential part is rigidly related to the density field (cf. Equation (112)). So, we have that E⊥∝k⊥nk and the spectrum of the mostly potential perpendicular electric field should be given by
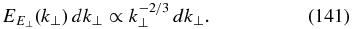
The spectrum of the parallel electric field is then found from  , which gives
, which gives
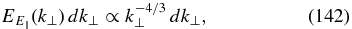
where we take into account the anisotropy predicted in the phenomenological model of Boldyrev & Perez (2012),  . The results of the measurements are shown in Figure 4. The top panel shows the spectrum of the perpendicular component of the electric field, compensated by the predicted k2/3. This component, by definition, follows the density spectrum in Figure 3. In contrast with the total energy spectrum, the density spectrum by itself does not exhibit a good power law in our inertial range of limited extent and neither does the spectrum of E⊥. The bottom panel of Figure 4 shows the spectrum of
. The results of the measurements are shown in Figure 4. The top panel shows the spectrum of the perpendicular component of the electric field, compensated by the predicted k2/3. This component, by definition, follows the density spectrum in Figure 3. In contrast with the total energy spectrum, the density spectrum by itself does not exhibit a good power law in our inertial range of limited extent and neither does the spectrum of E⊥. The bottom panel of Figure 4 shows the spectrum of  , compensated by the best fit power law in the interval k ∈ [5, 15] (the inertial interval in Figure 3). Although no definite power law is observed, the best fit based on this entire range is given by
, compensated by the best fit power law in the interval k ∈ [5, 15] (the inertial interval in Figure 3). Although no definite power law is observed, the best fit based on this entire range is given by  , with
, with  fitting better at the lower end and
fitting better at the lower end and  fitting better at the higher end of this range. Although the −1.4 scaling is close to our phenomenological estimate, the much steeper behavior in the rest of the interval is not yet understood. Note, however, that a steep
fitting better at the higher end of this range. Although the −1.4 scaling is close to our phenomenological estimate, the much steeper behavior in the rest of the interval is not yet understood. Note, however, that a steep  spectrum at subproton scales has also been recently observed in the solar wind (Mozer & Chen 2013).
spectrum at subproton scales has also been recently observed in the solar wind (Mozer & Chen 2013).
Figure 4. Energy spectrum of the electric field perpendicular to the field, E⊥∝∇⊥n (top panel) and the electric field parallel to the field,  (bottom panel) in strong kinetic-Alfvén turbulence at subproton scales, obtained from the numerical simulations of Equations (139) and (140) with a resolution of 5123 (Boldyrev & Perez 2012). k⊥ is plotted on the horizontal axis.
(bottom panel) in strong kinetic-Alfvén turbulence at subproton scales, obtained from the numerical simulations of Equations (139) and (140) with a resolution of 5123 (Boldyrev & Perez 2012). k⊥ is plotted on the horizontal axis.
Download figure:
Standard image High-resolution imageFrom a practical point of view, the electric field is not easy to measure since it depends of the frame of the observations (e.g., Bale et al. 2005; Chen et al. 2011). The electric field measured in the moving frame must be transformed to the rest frame of the plasma before its spectrum is calculated. In the case of the solar wind, this procedure requires subtraction of a large quantity, vsw × B, from the electric field measured by a satellite, where vsw is the solar-wind velocity relative to the satellite. In contrast, the  electric field is Galilean invariant and its measurements are frame-independent.
electric field is Galilean invariant and its measurements are frame-independent.
9. A NOTE ON WHISTLER TURBULENCE
As we pointed out in Section 7, the kinetic-Alfvén equations (118) and (119) are structurally identical to the reduced EMHD equations (128) and (129). This fact ensures that the scaling properties of kinetic-Alfvén turbulence and EMHD turbulence should be identical in the limit  . Strong EMHD turbulence has been numerically studied in the literature previously (e.g., Biskamp et al. 1999; Cho & Lazarian 2009), where a magnetic energy spectrum closer to −7/3 has been reported. As discussed in the previous section, the spectrum observed in our simulations is steeper than −7/3; a complete understanding of this steepening will probably require higher numerical resolution. We should, however, point out that the systems studied in previous works are not identical to our system (Equations (139) and (140)). For example, the studies of Biskamp et al. (1999) addressed three-dimensional decaying EMHD turbulence without a background field. In addition, their equations were also different from Equation (127), as they included terms associated with the finite electron inertia length de = c/ωpe.
. Strong EMHD turbulence has been numerically studied in the literature previously (e.g., Biskamp et al. 1999; Cho & Lazarian 2009), where a magnetic energy spectrum closer to −7/3 has been reported. As discussed in the previous section, the spectrum observed in our simulations is steeper than −7/3; a complete understanding of this steepening will probably require higher numerical resolution. We should, however, point out that the systems studied in previous works are not identical to our system (Equations (139) and (140)). For example, the studies of Biskamp et al. (1999) addressed three-dimensional decaying EMHD turbulence without a background field. In addition, their equations were also different from Equation (127), as they included terms associated with the finite electron inertia length de = c/ωpe.
Work by Cho & Lazarian (2009) contains simulations of EMHD with a strong background magnetic field, which make their setup closer to ours. However, these simulations also concentrate on decaying turbulence, which does not reach a steady state. The initial conditions in those runs deviate from the critical balance that would be needed in order to ensure strongly nonlinear coupling. Considering their ranges of initially populated  and k⊥, one estimates that the parameter
and k⊥, one estimates that the parameter  is somewhere between 0.7 and 5 at large scales, so turbulence may be already on the "weaker" side at the beginning of the evolution (in comparison, in our runs, this parameter is kept between 0.5 and 1). As the fluctuations decay, turbulence becomes progressively weaker since the background field does not change. In addition, both papers (Biskamp et al. 1999; Cho & Lazarian 2009) employ hyperviscosities and run at lower spatial resolutions compared with our runs.
is somewhere between 0.7 and 5 at large scales, so turbulence may be already on the "weaker" side at the beginning of the evolution (in comparison, in our runs, this parameter is kept between 0.5 and 1). As the fluctuations decay, turbulence becomes progressively weaker since the background field does not change. In addition, both papers (Biskamp et al. 1999; Cho & Lazarian 2009) employ hyperviscosities and run at lower spatial resolutions compared with our runs.
The regime of weak whistler turbulence has also been addressed in the literature for the cases of both parallel and oblique propagation with respect to the magnetic field (Livshitz & Tsytovich 1972; Boldyrev 1995; Galtier & Bhattacharjee 2003, 2005). In the limit of oblique propagation, which is more relevant to our consideration, the spectrum of weak whistler turbulence was studied in Boldyrev (1995) and Galtier & Bhattacharjee (2003). In these works, it was found that the kinetic equation for the energy spectrum had a formal steady biscaling solution

which should correspond to a constant energy flux in k-space. Galtier & Bhattacharjee (2003) also presented an elegant heuristic analysis that allowed the deviation of the anisotropic whistler spectrum (Equation (143)) from dimensional arguments. The same energy spectrum has also been derived for weak kinetic-Alfvén turbulence by Voitenko (1998), which agrees with the established similarity between the kinetic-Alfvén equations and the REMHD equations; see our discussion at the end of Section 7. It was, however, pointed out in Boldyrev (1995) that the formal solution (Equation (143)) is non-local, that is, the collision integral in the wave kinetic equation diverges logarithmically for such a spectrum at low wavenumbers. The question of whether the formal solution (Equation (143)) or a solution with the exponents close to those in Equation (143), is physically realizable therefore requires further study (e.g., Zakharov et al. 1992, Chapter 3).
10. CONCLUDING REMARKS
We presented a systematic study of subproton turbulence in a collisionless plasma, in the case of plasma beta ∼1. Our work is based on a full kinetic derivation, which complements previously available fluid-like, gyrokinetic derivations and numerical solutions of the Vlasov–Maxwell equations (e.g., Hollweg 1999; Howes et al. 2006, 2008a; Gary & Smith 2009; Schekochihin et al. 2009; Sahraoui et al. 2012). As we demonstrated, the full kinetic derivation allows one to effectively address the dynamics of kinetic-Alfvén and whistler modes in both linear and nonlinear regimes at subproton scales.
These modes have principal differences, which can be characterized from both formal mathematical and physical points of view. The regions of phase space where the kinetic-Alfvén and the whistler modes exist are shown in Figures 1 and 2. The kinetic-Alfvén modes occupy region I in these figures, both below and above the ion-cyclotron frequency Ωi. More specifically, they exist in the phase space region ω ≪ kvTi and kzρi ≪ 1. The whistler modes occupy an essentially different region II in Figure 1; more specifically, the region kzvTe ≫ ω ≫ kvTi and kzρi ≫ 1.
The physical difference between kinetic-Alfvén and whistler modes is in the dynamics of the ions. In kinetic-Alfvén fluctuations, the ions are dynamically important; they rapidly adjust to the fluctuating electric potential in the plasma. The kinetic-Alfvén fluctuations are essentially compressible and they are described by the kinetic-Alfvén system (Equations (118) and (119)). In the case of whistler modes, on the other hand, the ions are dynamically irrelevant; they provide a uniform stationary background, which, together with the quasi-neutrality condition, ensures effective incompressibility of the whistler modes. The whistler fluctuations are electron fluctuations; they are described by the EMHD equations (Equation (127)) or the REMHD equations (Equations (128) and (129)).
The kinetic-Alfvén and whistler modes share the same dispersion relation scaling, which may cause ambiguity when these waves are identified in numerical simulations or observations. In addition, as we discussed in Section 7, the corresponding non-dimensional fluid-like models have similar structures that may artificially blur their differences. Analysis of the ion dynamics helps to remove a possible ambiguity in such cases. In particular, analysis of the ion dynamics allows one to classify the subproton oscillations obtained by different methods in the literature. For example, according to our results, the modes obtained numerically in Sahraoui et al. (2012, Figure 3) for large propagation angles θ > 80° would be classified as kinetic-Alfvén waves, not whistlers. Indeed, the ion dynamics are essential for these modes since ω < k⊥vTi.9 Similarly, the system of equations derived from gyrokinetics in Schekochihin et al. (2009, Equations (226) and (227)) is essentially the kinetic-Alfvén system in our classification; it agrees with our Equations (118) and (119). Although, as we have demonstrated in the present work, these equations are applicable both above and below the ion gyrofrequency, they are different from the REMHD equations (Equations (134) and (135)); they do not describe oblique whistler waves, for example.
Finally, we comment on an interesting possibility that in the case when the kinetic-Alfvén frequency is comparable to the ion-cyclotron frequency, the kinetic-Alfvén modes may couple to the ion-Bernstein modes (e.g., Howes et al. 2008b; Podesta 2012; Chen et al. 2013b). The ion-Bernstein waves have a frequency satisfying  . The collisionless ion damping of these modes is negligible when
. The collisionless ion damping of these modes is negligible when  . From the dispersion relation of kinetic-Alfvén waves (Equation (41)), we see that ωka ∼ Ωi is satisfied when
. From the dispersion relation of kinetic-Alfvén waves (Equation (41)), we see that ωka ∼ Ωi is satisfied when  , where we assumed βi ∼ 1. The collisionless damping is therefore negligible when
, where we assumed βi ∼ 1. The collisionless damping is therefore negligible when  . In this limit, however, the ion-Bernstein modes occupy a narrow band in frequency space and they may not couple effectively to the kinetic-Alfvén modes. In the opposite case, when k⊥ρi is not large, these modes are relatively strongly damped compared with the kinetic-Alfvén modes (e.g., Podesta 2012) and they also may not be effectively generated.
. In this limit, however, the ion-Bernstein modes occupy a narrow band in frequency space and they may not couple effectively to the kinetic-Alfvén modes. In the opposite case, when k⊥ρi is not large, these modes are relatively strongly damped compared with the kinetic-Alfvén modes (e.g., Podesta 2012) and they also may not be effectively generated.
We are grateful to Christopher Chen and Vladimir Mirnov for useful comments. This work was supported by the U.S. DOE award DE-SC0003888, the DOE grant DE-SC0001794, the NSF grant PHY-0903872, and the NSF Center for Magnetic Self-organization in Laboratory and Astrophysical Plasmas at the University of Wisconsin–Madison. High Performance Computing resources were provided by the Texas Advanced Computing Center (TACC) at the University of Texas at Austin under the NSF-Teragrid Project TG-PHY080013N.
Footnotes
- 3
It is interesting to note that the same dispersion relation also holds for the case of cold electrons, that is, ω ≫ kzvTe, (e.g., Aleksandrov et al. 1984). This situation, however, requires the plasma beta to be small, βe ≪ 1; this limit is not considered here.
- 4
The other solution is the ion-acoustic mode
 , which is not allowed by the condition kvTi ≪ ω ≪ kzvTe, unless Te ≫ Ti. The limit of strongly non-isothermal plasma is, however, not considered in this work.
, which is not allowed by the condition kvTi ≪ ω ≪ kzvTe, unless Te ≫ Ti. The limit of strongly non-isothermal plasma is, however, not considered in this work. - 5
We set aside the fact that the unperturbed distribution function may be non-Maxwellian. We plan to address more general cases in a future study.
- 6
Once again, we do not consider possible non-Maxwellian solutions here.
- 7
This fact can also be seen directly from Equation (1), where we can neglect the term qi[v × B]∂fi/∂p compared with v∂fi/∂x, due to k⊥ρi ≫ 1.
- 8
- 9
In Sahraoui et al. (2012), the mode existing in region I and extending both below and above the ion gyrofrequency is referred to as a kinetic-Alfvén- whistler mode. While this fact is only a semantic difference and our study does not contradict their work, we prefer to adhere to the common definition in order to avoid possible confusion and call the whistler the electron mode (existing in region II), while retaining the term kinetic-Alfvén wave for the mode in region I.









