ABSTRACT
In the version of the single-degenerate scenario of Type Ia supernovae (SNe Ia) studied here, a carbon–oxygen white dwarf explodes close to the Chandrasekhar limit after accreting material from a non-degenerate helium (He) companion star. In the present study, we employ the Stellar GADGET code to perform three-dimensional hydrodynamical simulations of the interaction of the SN Ia ejecta with the He companion star taking into account its orbital motion and spin. It is found that only 2%–5% of the initial companion mass is stripped off from the outer layers of He companion stars due to the supernova (SN) impact. The dependence of the unbound mass (or the kick velocity) on the orbital separation can be fitted to a good approximation by a power law for a given companion model. After the SN impact, the outer layers of a He donor star are significantly enriched with heavy elements from the low-expansion-velocity tail of SN Ia ejecta. The total mass of accumulated SN-ejecta material on the companion surface reaches about ≳ 10−3 M☉ for different companion models. This enrichment with heavy elements provides a potential way to observationally identify the surviving companion star in SN remnants. Finally, by artificially adjusting the explosion energy of the W7 explosion model, we find that the total accumulation of SN ejecta on the companion surface is also dependent on the explosion energy with a power-law relation to a good approximation.
1. INTRODUCTION
Type Ia supernovae (SNe Ia) are instrumental as distance indicators on a cosmic scale to determine the expansion history of the universe (Riess et al. 1998; Schmidt et al. 1998; Perlmutter et al. 1999). However, neither observational nor theoretical approaches have been able to identify the nature of SN Ia progenitors and details of the explosion mechanism remain unclear (see Hillebrandt & Niemeyer 2000; Hillebrandt et al. 2013 for a review). Recently, the nearby SN 2011fe (Nugent et al. 2011; Li et al. 2011) has been used as an important test case to constrain SN Ia explosion scenarios (Röpke et al. 2012) since it can be observed in unprecedented detail. However, additional investigations are still required to put more constraints on SN Ia explosions.
It is widely believed that SNe Ia originate from thermonuclear explosions of carbon–oxygen (CO) white dwarfs (WDs) in binary systems. Depending on the nature of the companion star, the most favored progenitor models of SNe Ia are classified into two general categories, the "single-degenerate" (SD) scenario (Whelan & Iben 1973; Nomoto 1982) and the "double-degenerate" (DD) scenario (Whelan & Iben 1973; Iben & Tutukov 1984; Webbink 1984). In the DD scenario, two CO WDs spiral in and merge due to gravitational wave radiation (GWR), causing a thermonuclear explosion of the merged system. Recently, some observational and hydrodynamical studies support the viability of DD models as the progenitors of SNe Ia (see, e.g., Li et al. 2011; Nugent et al. 2011; Chomiuk et al. 2012; Horesh et al. 2012; Bloom et al. 2012; Schaefer & Pagnotta 2012; Pakmor et al. 2010, 2011, 2012b, 2013). In contrast, previous simulations suggested that the DD scenario likely leads to an accretion-induced collapse rather than a SN Ia (Nomoto & Iben 1985; Timmes et al. 1994).
In the SD scenario, a CO WD increases its mass by accreting material from a non-degenerate companion star (a slightly evolved main sequence (MS) star, a red giant (RG) or a He star (HE)) to approach the critical explosion mass (just below the Chandrasekhar limit MCh ∼ 1.44 M☉) to ignite a SN Ia explosion. There is evidence from observations supporting that the progenitors of some SNe Ia come from the SD channel. For example, the pre-supernova (SN) circumstellar matter has been detected, and the features of the interaction of the SN explosion with circumstellar matter are seen in observations (see, e.g., Patat et al. 2007; Sternberg et al. 2011; Foley et al. 2012; Dilday et al. 2012; Shen et al. 2013). However, only a fairly narrow range of accretion rates is allowed in order to avoid nova explosions in the SD case, making it difficult to explain the observed nearby SN Ia rate (Nomoto 1982; Nomoto et al. 2007; Ruiter et al. 2009; Wang et al. 2010).
In recent years, the WD+MS and WD+RG progenitor models have been invoked to explain the observed long-delay-time (≳ 1 Gyr) population of SNe Ia (see, e.g., Ruiter et al. 2009; Wang & Han 2010; Wang et al. 2010; Maoz & Badenes 2010; Maoz et al. 2010; Maoz & Mannucci 2012). Numerically, the impact of a SN Ia explosion on a MS-like or a RG companion star has been studied with hydrodynamical simulations by several authors (see, e.g., Marietta et al. 2000; Pakmor et al. 2008; Pan et al. 2010, 2012; Liu et al. 2012, 2013). They found that ∼0.03–0.15 M☉ H-rich material can be stripped off from the surface of MS companion stars. For RG companions it is believed that the entire envelope is stripped off by the SN impact. This high stripped mass is far larger than the most stringent upper limit of 0.01 M☉ which Leonard (2007) derived from the non-detection of Hα emission in late-time spectra (see also Shappee et al. 2013). So far, in fact, no direct observation shows the signature of stripped H-rich material, which seriously challenges the SD progenitor scenario.
In the spin-up/spin-down model for SNe Ia,8 however, the donor star might shrink significantly because it exhausts the H-rich envelope before the explosion sets in after a spin-down phase of >105 yr. Thus, the donor star could be too dim to detect by the time of explosion and much smaller than its Roche lobe (see Di Stefano et al. 2011; Justham 2011). This may reduce the possibility of the detection of H lines in SN Ia nebular spectra and possibly provides an explanation for the apparent lack of a "left-over" star in LMC SN remnant SNR 0609-67.5 (Di Stefano & Kilic 2012).
In the so-called WD+HE channel a CO WD accretes material from a He companion star. This may initiate a thermonuclear explosion of the WD. At present, two possible explosion models are frequently discussed: the sub-MCh scenario (Woosley & Weaver 1994; Fink et al. 2007, 2010; Woosley & Kasen 2011) and the MCh scenario (Wang et al. 2009a, 2009b). In this paper, however, we only focus on the WD+HE MCh model. With a binary population synthesis approach, Wang et al. (2009b, hereafter WMCH09) comprehensively and systematically investigated WD+HE MCh systems and showed that this channel can explain SNe Ia with short delay times (≲ 108 yr), which is consistent with recent observational implications of young populations of SN Ia progenitors (Wang et al. 2009a, 2009b).
Recently, Pan et al. (2010, 2012) investigated the impact of SN Ia ejecta on a He companion star including the rotation of the He star by using Eulerian hydrodynamics simulations with the FLASH code. They found the He companion star could be contaminated by the SN Ia ejecta in its outer envelope after the impact, and the nickel contamination is ∼10−4 M☉ (Pan et al. 2010, 2012). This might help to identify surviving companion stars in the remnants of historical SNe Ia even a long time after the explosion. In their simulations, however, the He star companion models were constructed by artificially adopting a constant mass-loss rate to mimic the detailed binary evolutionary models of WMCH09.
In this work, we update the He companion star models with one-dimensional (1D) consistent binary evolution calculations. Then, we perform hydrodynamics simulations of the interaction of SN Ia ejecta with He companion stars. To this end we use the three-dimensional (3D) smoothed particle hydrodynamics (SPH) code Stellar GADGET. In Section 2, the code and the initial setup are introduced. The results of the SPH impact simulations are discussed on the basis of two consistent He companion star models in Section 3. All numerical results are presented in Section 4. Finally, we summarize our results and conclude in Section 5.
2. CODES AND INITIAL MODELS
We use Eggleton's stellar evolution code (Eggleton 1971, 1972, 1973) to follow the detailed binary evolution of WD+HE progenitor systems. The Roche lobe overflow (RLOF) is treated in the code as described by Han & Podsiadlowski (2004). In this work, we only focus on MCh explosions of accreting WDs. The influence of rotation on the He-accreting WDs is not considered in the stellar evolution calculations. Our basic input physics and initial setup in the code are the same as those in WMCH09. The He companion star is evolved without enhanced mixing, i.e., the convective overshooting parameter, δov = 0 (see Dewi et al. 2002). Initial He star models are set up with a He abundance of Y = 0.98 and a metallicity of Z = 0.02. In addition, orbital angular momentum loss due to GWR is included by adopting a standard formula presented by Landau & Lifshitz (1971):
where G, c, MWD and M2 are the gravitational constant, vacuum speed-of-light, mass of the accreting WD and mass of the He companion star, respectively.
We start to trace the binary evolution when the WD+HE binary system is formed. The mass transfer occurs through RLOF once the He donor star fills its Roche lobe. Here, we do not solve the stellar structure equations for the WD star when the structures of the companion stars are constructed. Instead, we used the optically thick wind model of Hachisu et al. (1996, 1999) and adopt the prescription of Kato & Hachisu (2004) for the mass accumulation efficiency of He-shell flashes onto the WD primary. If the mass transfer rate, , is above a critical value, , we assume that He burns steadily on the surface of the WD and that the He-rich material is converted into carbon and oxygen at the rate , while the unprocessed matter is assumed to be lost from the system as an optically thick wind at a mass-loss rate . The critical mass-accretion rate is (Nomoto 1982)
When is smaller than , the following assumptions have been adopted.
- 1.If , it is assumed that there is no mass loss and that He-shell burning is steady, where is the minimum accretion rate of stable He-shell burning from Kato & Hachisu (2004).
- 2.If , He-shell burning is unstable, He-shell flashes occur and a part of the envelope mass is assumed to be blown off from the surface of the WD. Here, is the minimum accretion rate of weak He-shell flashes (Woosley et al. 1986).
- 3.If , He-shell flashes are so strong that no mass can be accumulated by the WD (i.e., the mass-growth rate of the WD is zero).
Finally, two He companion star models based on detailed binary evolution calculations are chosen as representative examples to perform SPH impact simulations. They are named "He01" and "He02." The typical binary evolution calculations of these two models are shown in Figure 1 (He01 model) and Figure 2 (He02 model). In the He01 model (companion mass , orbital separation A = 5.16 × 1010 cm, companion radius R2 = 1.91 × 1010 cm) the companion star remains to be a He MS star (central He burning), whereas in the He02 model (, A = 7.04 × 1010 cm, R2 = 2.48 × 1010 cm) it has evolved slightly into the subgiant phase (central He exhausted) at the onset of the SN Ia explosion. The structure profiles of two companion stars (the He01 and He02 models) at the moment of SN Ia explosion are shown in Figure 3.
Figure 1. (a) The solid, dashed and dash-dotted curves show the mass transfer rate from the secondary, , the mass-growth rate of the CO WD, , and the mass of the CO WD, MWD, varying with time, respectively. (b) The evolutionary track of the He donor star is shown as a solid curve and the evolution of orbital period is shown as a dash-dotted curve. Note that the He companion is still a MS star at the moment of the SN explosion.
Download figure:
Standard image High-resolution imageFigure 2. Same as Figure 1, but for the He companion star that slightly evolves to the subgiant (SG) phase at the moment of SN explosion.
Download figure:
Standard image High-resolution imageFigure 3. Profiles of the density ρ, pressure P, and helium abundance Y as a function of enclosed mass m at the moment of the SN explosion for the He01 model (solid lines) and He02 model (dashed lines).
Download figure:
Standard image High-resolution imageThe hydrodynamical simulations of the impact of SN Ia ejecta on the He companion star are performed with the 3D SPH code Stellar GADGET (Pakmor et al. 2012a; Springel 2005). In our simulation, we use the same method as Liu et al. (2012) to map the 1D profiles of density and internal energy of a 1D companion star model to a particle distribution suitable for the SPH code. To reduce numerical noise introduced by the mapping, the SPH model of each companion star is relaxed for several dynamical timescales (1.0 × 104 s) before we start the actual impact simulations. If the relaxation succeeds, the velocities of the particles stay close to zero. Otherwise, we reject the SPH model, and repeat the relaxation after adjusting the relaxation parameters (Pakmor et al. 2012a).
The SN explosion is represented by the W7 model of Nomoto et al. (1984) and Maeda et al. (2010). This model has been shown to provide a good fit to the observational light curves of SNe Ia (Lentz et al. 2001). Its total explosion energy is 1.23 × 1051 erg, the average velocity of the ejecta 104 km s−1. Based on the 1D W7 model of Nomoto et al. (1984), SPH particles are placed randomly in shells to reproduce the mass (density) profile and gain the radial velocities they should have at their positions (all particles have the same mass). The composition of a particle is then set to the values of the initial 1D model at a radius equal to the radial coordinate of the particle. In our hydrodynamical simulations, the impact of the SN Ia ejecta on the companion is simulated for ⩾2000 s taking into account the orbital motion and spin of the He companion star. Here, we assume that the rotation of the companion star is phase-locked to its orbital motion. Moreover, we set the x − y plane as the orbital plane of the binary system with an assumption of a circular orbit. The z-axis is chosen as the rotation axis, and, when the spin of the companion star is included, the positive z-axis is the direction of the angular momentum.
3. SIMULATIONS
3.1. Resolution Test
We use the W7_He01 model (see Table 1) as a typical case to perform a convergence test to check the sensitivity of unbound mass to different resolutions. By adopting a fixed orbital separation (A = 5.16 × 1010 cm), the resolutions are set up with different numbers of total SPH particles ranging from 2.64 × 104 to 1.05 × 107. The unbound companion mass caused by the SN impact as a function of time since explosion for each resolution is plotted in Figure 4. The unbound mass is calculated by summing up the total mass of all particles that originally belonged to the He companion star but are unbound after the impact. In order to determine whether or not a particle is bound to the star, we calculated the total energy of each particle at each time step, Etot = Ekin + Epot + Ein, where Ekin, Epot and Ein are the kinetic energy (positive), the potential energy (negative) and the internal energy (positive), respectively. If Etot > 0, the particle is unbound. Note that the center-of-mass motion of the star is subtracted when calculating the kinetic energy for each particle.
Figure 4. Unbound companion mass vs. time since explosion in W7_He01 model for different resolutions (∼104–107 SPH particles in the simulations).
Download figure:
Standard image High-resolution imageTable 1. Results of SPH Impact Simulations
| Modela | vorb | vspin | R2 | A | Munbound | vkick | δMtotb | δMFeb | δMNib | MNi/MHe c | MFe/MHe c |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (km s−1) | (1010 cm) | (M☉) | (km s−1) | (10−3 M☉) | (10−3) | (10−3) | |||||
| W7_He01 | ⋅⋅⋅ | ⋅⋅⋅ | 1.91 | 5.16 | 0.027 | 66.39 | 5.22 | 3.52 | 1.59 | 1.63 | 3.62 |
| W7_He02 | ⋅⋅⋅ | ⋅⋅⋅ | 2.48 | 7.04 | 0.056 | 58.75 | 3.12 | 2.16 | 0.88 | 3.54 | 8.72 |
| W7_He01_r | 432 | 301 | 1.91 | 5.16 | 0.028 | 66.94 | 5.37 | 3.49 | 1.81 | 1.85 | 3.57 |
| W7_He02_r | 387 | 237 | 2.48 | 7.04 | 0.057 | 59.74 | 3.14 | 2.02 | 0.96 | 3.86 | 8.11 |
| W708_He01_r | 432 | 301 | 1.91 | 5.16 | 0.019 | 39.93 | 12.06 | 7.49 | 4.44 | 4.52 | 7.61 |
| W710_He01_r | 432 | 301 | 1.91 | 5.16 | 0.024 | 52.53 | 8.30 | 5.29 | 2.91 | 2.97 | 5.39 |
| W714_He01_r | 432 | 301 | 1.91 | 5.16 | 0.033 | 75.89 | 3.97 | 2.57 | 1.38 | 1.38 | 2.64 |
| W716_He01_r | 432 | 301 | 1.91 | 5.16 | 0.037 | 86.08 | 2.71 | 1.80 | 0.87 | 0.90 | 1.86 |
Notes. a"W7" corresponds to the W7 explosion model (Nomoto et al. 1984; Maeda et al. 2010). "W708," "W710," "W714" and "W716" present W7-like models that are produced by adjusting the original W7 model with different explosion energies (0.8, 1.0, 1.4 and 1.6 × 1051 erg). Note that all parameters but the SN energy are kept constant with the values of the original model (see also Pakmor et al. 2008). "He01" and "He02" are two He companion models. "r" means that the orbital motion and spin of the He companion are included. bδMtot, δMFe and δMNi are the total contamination, the accreted Fe and Ni mass at the end of the simulations (≳ 2000 s after the explosion), respectively. cThe ratio of bound Ni and Fe masses (without decay) to the He masses of a surviving star. Please note that the initial metallicity of the He star is not included.
Download table as: ASCIITypeset image
Figure 4 shows that the amount of unbound companion mass asymptotically approaches a final value at late times. For the simulations that span a range of 400 in mass resolution from the lowest to the highest mass resolution the stripped mass measured in those simulations deviates less than 25% from the highest resolution run. Therefore, our results are clearly sufficiently well converged to allow a meaningful comparison to observational constraints, which are still uncertain by a factor of a few (Leonard 2007). Note that we also carried out the convergence test for the amount of SN ejecta that are captured by the companion star after the SN explosion (for different resolutions of ∼2.64 × 104–1.06 × 107, the captured SN-ejecta masses at the end of simulations are 0.0064, 0.0067, 0.0075, 0.0072, 0.0060, 0.0059, and 0.0053 M☉). We found that it is also sufficiently well converged. Therefore, we chose the level of 5 million SPH particles to represent the He companion stars (which corresponds to the total particles of ∼107) in all following impact simulations.
3.2. Typical Evolution after the SN Ia Explosion
Figure 5 illustrates the temporal density evolution of the SN ejecta and companion material of our hydrodynamics simulations for the W7_He01 model. Before the SN explosion, the He companion star is filling its Roche lobe. The WD explodes as a SN Ia on the right side of the companion star. The SN ejecta expand freely for a while before hitting the surface of the donor star which faces toward the explosion (see first snapshot). A shock wave develops while the He-rich material is stripped off from the companion star. This shock wave propagates through the whole companion star and strips off additional material from the far side of the companion. As the SN ejecta flow around the companion star, a cone-shaped hole with an opening angle with respect to the x-axis of ∼35° forms in the SN ejecta (see Figure 5). At the end of the hydrodynamics simulations, about 0.027 M☉ of He-rich material is stripped off due to the SN impact. The companion star survives the explosion, but it is completely out of thermal equilibrium and dramatically expanding due to the SN heating. Compared with our previous work on WD+MS models (Liu et al. 2012), this effect is more significant since He companion stars have higher orbital velocities.
Figure 5. Temporal evolution of the density structure of SN and companion material in impact simulations with the W7_He01 model. The color scale indicates the logarithm to base 10 of density in g cm−3. The plots are made using the freely available SPLASH code (Price 2007).
Download figure:
Standard image High-resolution imageFigure 6 shows how the orbital motion and the spin of the He companion star affect the density structures of the SN ejecta and the companion star. In this work, the hydrodynamics simulations are carried out for He01 and He02 models (see Table 1) by including their orbital and spin velocities. All simulated results are shown in Table 1. Note that "W7" means the W7 explosion model, the letter "r" indicates that the orbital motion and spin of the companion star are included into the simulations. It is evident that the additional unbound mass and kick velocity caused by including the orbital motion and spin are very small (see Table 1), the difference being within 2% compared to non-rotating models.
Figure 6. Same as Figure 5, but for the W7_He01_r model (which includes the orbital motion and spin of He companion). The color scale indicates the logarithm to base 10 of density in g cm−3. The plots are made using the freely available SPLASH code (Price 2007).
Download figure:
Standard image High-resolution image3.3. Parameter Study
At the end of the simulations, only 0.03–0.06 M☉ of He-rich companion material is found to be stripped off in impact simulations of two different He companion models. Meanwhile, the companion star receives a small kick velocity of ∼58–67 km s−1 at the end of the simulations. In order to explore the sensitivity of the numerical results to the orbital separation, we run several simulations by artificially adjusting the binary separations of the "W7_He01" and "W7_He02" models. All other parameters are kept constant at the values of the original model. Figure 7 shows the unbound mass and kick velocity as functions of the binary orbital separations, which is consistent with other similar impact hydrodynamics simulations (Pan et al. 2010, 2012). For a given companion model, the unbound mass decreases as the separation becomes larger. It is found that this relation follows a power law to a good approximation, and can be fitted as (see Figure 7(a)):
where A is the binary separation, R2 is the radius of the He companion star at the onset of the SN explosion, C1 is a constant and α is the power-law index. All fitting parameters are listed in Table 2. Moreover, the dependence of the kick velocity, vkick, on A/R2 can also be fitted by a power law (see Figure 7(b)):
where C2 is a constant and β is the power-law index (see Table 2).
Figure 7. Mass stripped off from the companion (a) and kick velocity (b) as functions of the ratio of the orbital separation to the radius of the companion, A/R2, for a given He companion model. The star and cross symbols represent the results of our impact simulations for the He01 model and He02 model. Lines show fitted power-law relations based on the numerical simulation results.
Download figure:
Standard image High-resolution imageTable 2. Fitting Parameters for Equations (3) and (4)
| Model | Fitting Parameters | |||
|---|---|---|---|---|
| C1 | α | C2 | β | |
| W7_He01 | 0.54 | 2.96 | 689 | 2.37 |
| W7_He02 | 0.34 | 1.75 | 247 | 1.38 |
Download table as: ASCIITypeset image
The different companion star models lead to different fitting parameters. This indicates that the companion structure plays an important role in our impact simulations also. For example, the binding energy of the companion envelope would affect it. In order to compare with other hydrodynamics simulations, the results of the He-WDc model of Pan et al. (2010; M2 = 1.007 M☉, A = 4.0 × 1010 cm and R2 = 1.35 × 1010 cm at the moment of the SN explosion)9 are chosen to compare with our W7_He02 model (M2 = 1.007 M☉, A = 7.04 × 1010 cm and R2 = 2.48 × 1010 cm). The unbound mass and kick velocity in their He-WDc model are more sensitive to the orbital separation than in our W7_He02 model (see Figure 7). The difference might be caused by different companion structures. In their 1D calculations, the mass transfer from the He companion star was modeled by adopting a constant mass-loss rate to mimic the work of WMCH09 (see Pan et al. 2010). The orbital separation at the moment of the SN explosion was calculated using the formulation of Eggleton (1983). In our consistent binary calculations, however, we trace the details of the binary evolution by treating the mass transfer as RLOF, which also fixes the separation of the binary system at this moment.
Based on the distribution of the parameter A/R2 in population synthesis calculations of WMCH09 (see Figure 8(a)), we simply calculate the unbound masses due to the SN impact by using Equation (3). The derived distribution for the unbound mass is shown in Figure 8(b), where the peak unbound mass ranges from 0.02 M☉ to 0.05 M☉.10 The difference between the W7_He02 and He-WDc models again indicates that the details of the companion structures are important for the interaction of SN Ia ejecta with the companion star.
Figure 8. (a) Distribution of the parameter A/R2 based on the population synthesis results for WD+HE models (Wang et al. 2009a). (b) The corresponding distribution of unbound mass due to the SN impact. The unbound mass is calculated by using the power-law relation of Equation (3).
Download figure:
Standard image High-resolution image4. DISCUSSION
4.1. Effect of Ablation
After the SN explosion, the unbound He-rich material from the companion star may result from two mechanisms: ablation (SN heating) and stripping (momentum transfer). Pan et al. (2012) found that the stripped-to-ablated mass ratio for the He-WD scenario was about 0.5–0.8 in their impact simulations with the FLASH code. They argued that previous analytical or semi-analytical work underestimated the unbound mass due to the neglect of ablation.
To obtain the stripped-to-ablated mass ratio, we compare the internal energy of a companion particle to its kinetic energy once it becomes unbound. If the internal energy is larger (or smaller) than the kinetic energy, we think the particle is ablated (or stripped). We then use the SPH particle's ID to trace all these ablated (or stripped) particles to the end of the simulations (2000 s after the impact). The total ablated (stripped) mass is calculated by summing the particles that are ablated (stripped) and still unbound at the end of the simulations. Finally, we obtain a stripped-to-ablated mass ratio of ∼0.5, which is consistent with the results of Pan et al. (2012).
Moreover, we calculate the amount of unbound mass by summing the total mass of all unbound particles for each time step, where we do include internal energy of the particle (i.e., Etot = Ekin + Epot + Ein, which corresponds to the dashed line in Figure 9) or do not (i.e., Etot = Ekin + Epot, which corresponds to the solid line in Figure 9). The companion particles are ablated and stripped and become unbound in an early stage of the explosion. As time goes by, the internal energy of the particles is converted into their kinetic energy. Moreover, some ablated and stripped particles become bound again. Already 1000 s after the explosion most of the internal energy deposited by the impact has been converted into kinetic energy (see Figure 9).
Figure 9. Unbound mass vs. simulation time in impact simulations with the W7_He01 model. The solid line shows the total mass of all particles with a total energy (kinetic plus potential energy) larger than zero. The dashed line also includes the internal energy in the sum.
Download figure:
Standard image High-resolution image4.2. Hole in the Ejecta
The SN impact affects not only the companion star, but also the SN ejecta themselves. He-rich material is stripped off from the companion due to the SN impact and largely confined to the downstream region behind the companion star, creating a hole in the SN ejecta with an opening angle of ∼35° with respect to the x-axis in our simulation (see Figures 5 and 10(a)). Recent hydrodynamic simulations suggest that the cone-hole that is created during the interaction could remain for hundreds of years (García-Senz et al. 2012). Kasen et al. (2004) explored the effect of a hole in the SN ejecta on spectra and light curves, suggesting that the cone-hole might be a source of polarization of SN Ia spectra. For a recent review of spectropolarimetry measurements of SNe Ia see Wang & Wheeler (2008).
Figure 10. (a) Distribution of opening angle of all unbound companion particles with respect to the x-axis at the end of the simulation. (b) Velocity distribution of unbound companion material.
Download figure:
Standard image High-resolution imageAfter the impact, stripped He-rich material is mixed with the SN ejecta (see Figure 11). More SN-ejecta material is found to be mixed into the He-filled hole if the orbital motion and spin of the He companion star are considered. The post-impact velocity distributions of the stripped companion material are shown in Figure 10(b). The peak velocity of ∼800 km s−1 moves rightward to ∼1000 km s−1 when the orbital and spin velocities of the companion star are included. However, this peak velocity is still smaller than the typical ejecta velocity of ∼104 km s−1, which indicates that the stripped He-rich material is largely hidden in the SN ejecta. It might be possible to detect it in late-time spectra of the SN when the ejecta become transparent (see also Pan et al. 2012). The high excitation energy of He, however, may prevent the formation of He lines in the nebular spectra.
Figure 11. Mass fraction of companion material to the SN ejecta in the hydrodynamics simulations of the W7_He01 (left panel) and W7_He01_r models (right panel). The blue end of the color table corresponds to pure SN-ejecta material while the red end of the color table represents pure companion material.
Download figure:
Standard image High-resolution image4.3. Accumulation of Ejecta on the Companion Star
4.3.1. Initial Velocities of Accreted SN Ejecta
The envelope of the companion star may be enriched by heavy elements of the SN Ia ejecta while its He-rich material is stripped off by the SN impact. As a consequence a surviving companion star may show unusual chemical signatures if a significant amount of SN-ejecta material is accumulated onto the donor star. González Hernández et al. (2009) concluded that Tycho G has an unusually high nickel abundance, and they claimed that it can be explained by the accumulation of SN ejecta. However, the measured [Ni/Fe] ratio from a more recent study of Kerzendorf et al. (2012) seems to be not unusual with respect to field stars with the same metallicity. Unusual abundances become a potential approach to identify the He companion stars in SNRs after the nickel radioactively decays.
In the hydrodynamics simulations, we trace all bound particles that originally belonged to the SN ejecta after the explosion. Figure 12 illustrates the temporal evolution of the amount of bound ejecta in the W7_He01 and W7_He02 models. After the SN explosion, it takes some time for the ejecta material to settle onto the surface of the companion star. Early after the SN explosion, most of the bound ejecta material is found at regions close to the SN explosion center. About 600–700 s after the impact, almost all bound ejecta particles fall onto the companion (see Figure 12) and mix with the outer layers of the star. At the end of the simulations (∼2000 s), the total amount of accreted SN ejecta is Mtot ∼ 3–5 × 10−3 M☉ (MNi ∼ 0.8–1.6 × 10−3 M☉ and MFe ∼ 2–4 × 10−3 M☉) for the W7_He01 and W7_He02 models. The bound nickel mass is similar to the results of the hydrodynamics simulations of Pan et al. (2012). In order to check whether some bound ejecta particles become unbound again at late times, we keep running the W7_He01 and W7_He02 models until 7000 s after the impact. It is found that some bound ejecta particles leave the companion star again; however, the change is only 1%–3%. Therefore, we run all other simulations in this work to only 2000–3000 s to save computational resources.
Figure 12. Temporal evolution of bound ejecta masses. Early in the SN explosion, most bound ejecta are found at the regions close to the SN explosion center.
Download figure:
Standard image High-resolution imageFigure 13 shows the abundances of various chemical elements accumulated from the SN ejecta onto the surface of the He companion star at the end of the simulations. Iron-peak elements (especially Fe and Ni) dominate the accreted ejecta (see the vertical gray color range of Figure 13). Note that the masses of unstable isotopes, such as 56Ni, 57Ni and 56Co are also included when summing up the Ni and Co masses. In order to check the original expansion velocity distribution of all accreted ejecta particles, we trace the original positions of all bound ejecta particles in the W7 model (t = 10 s) based on their SPH ID number. The result is shown in Figure 14(a). Most of the contamination is attributed to particles with low expansion velocity in the SN ejecta (i.e., the innermost region of the W7 model). The typical peak expansion velocity of accreted ejecta material is ∼103 km s−1. This result can be explained by the lower kinetic energy of those particles which makes it easier to stay at the surface of the companion star after the momentum transfer. The distribution of initial expansion velocities of all accreted iron-peak elements (Cr, Mn, Fe, Co and Ni, which corresponds to the vertical gray range of Figure 13) is further shown in Figure 14(b). Again, most accreted iron-peak elements come from the low-velocity tail of the SN ejecta. Therefore, we argue that the composition of the ejecta material that pollutes the companion star is very sensitive to the nuclear burning at the center of the explosion and could, if detected, possibly be used as a diagnostic of the explosion mechanism.
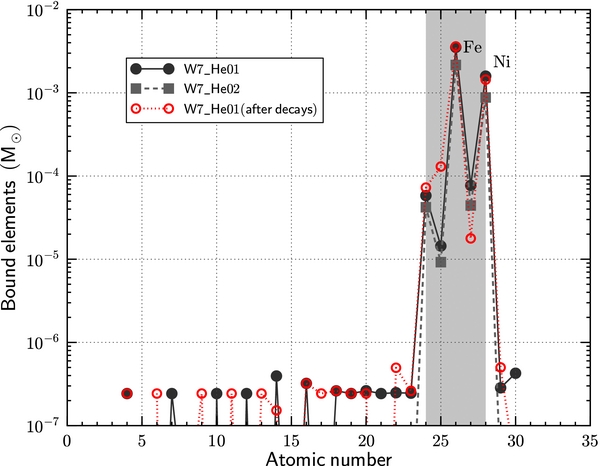
Figure 13. Chemical composition of the accreted ejecta material ∼2000 s after the explosion for the W7_He01 and W7_He02 models. The corresponding composition of the accreted ejecta after decays of unstable isotopes for the W7_He01 model is shown with open circles.
Download figure:
Standard image High-resolution imageFigure 14. (a) Distribution of bound ejecta in their initial expansion velocity space (at 10 s after the explosion). (b) Similar to (a), but only includes the iron-peak elements of the W7_He02 model (Cr, Mn, Fe, Co and Ni) which correspond to the vertical gray range of Figure 13.
Download figure:
Standard image High-resolution image4.3.2. Influence of Orbital Separation
We checked the sensitivity of the level of total contamination to the orbital separation for a given companion model. The orbital separation is adjusted to cover the range of the A/R2 parameter suggested by population synthesis calculations as shown in Figure 8(a). Figure 15 illustrates how the contamination depends on the orbital separation in the W7_He01 and W7_He02 models. The amount of SN Ia ejecta deposited on the surface of the He companion star is seen to vary with the orbital separation for a fixed companion model. Larger orbital separation leads to a lower ram pressure and also a smaller cross section, reducing the contamination from SN Ia ejecta. Note, however, that the changes in the orbital separation of the W7_He01 or W7_He02 model are purely artificial. Therefore, the effect of the nature of the He companion star is ignored. The different amount of contamination between W7_He01 and W7_He02 indicates that the details of the companion structure are also important.
Figure 15. Dependence of bound-ejecta mass on the orbital separation in impact simulations with the W7_He01 (square markers) and W7_He02 models (star markers). All values are measured at the end of the SPH impact simulations.
Download figure:
Standard image High-resolution imageMoreover, the comparison between the results of the W7_He01 (or W7_He02) and W7_He01_r (or W7_He02_r) models shows that the asymmetry due to the orbital motion and spin of the He companion star does not significantly affect the amount of the contamination of SN ejecta in our hydrodynamical simulations (see Table 1).
4.3.3. Influence of the Explosion Energy
A 1D parameterized pure deflagration of a MCh CO WD with a kinetic energy of 1.23 × 1051 erg (i.e., the W7 model; see Nomoto et al. 1984) is used to represent the SN Ia explosion in our hydrodynamics simulations. However, different deflagration and detonation cases cover a typical range of kinetic energies of 0.8–1.6 × 1051 erg (Röpke et al. 2007; Gamezo et al. 2005; Seitenzahl et al. 2013). Here, we study how different explosion energies affect the interaction with the companion star.
For this purpose, we use the same method as Pakmor et al. (2008) to artificially adjust the kinetic energy of the SN ejecta by scaling the velocities vi of the SN particles based on the original W7 model (see also Pakmor et al. 2008):
where and vW7 are the kinetic energy (1.23 × 1051 erg) and homologous expansion velocity of the ejecta (which corresponds to velocities of expanding shells of SN ejecta) of the original W7 explosion model. This scaling preserves the homologous expansion (v∝r) of the ejecta. Four additional W7-based models with different kinetic energies (, and 1.6 × 1051 erg) are studied. The lowest of these kinetic energies is consistent with simulations of pure deflagrations in CO WDs (e.g., Röpke et al. 2007). The upper limit is calculated by assuming that a MCh WD consisting of an equal-by-mass mixture of carbon and oxygen burns completely to 56Ni.
Using the "He01_r" model as a representative case, we investigate the influence of the SN explosion energy on the stripped companion mass, kick velocity and deposited ejecta mass. Numerical results for all W7-based models are shown in Table 1. The stripped mass increases linearly with SN explosion energy (see Figure 16(a)). With a typical range of explosion energies of 0.8–1.6 × 1051 erg, the companion mass stripped by the SN impact changes by a factor of two. This is consistent with the study of Pakmor et al. (2008) for MS companion stars. Moreover, the dependence of kick velocity and captured ejecta mass on the explosion energy can be fitted with a power law to a good approximation (see Figures 16(b) and (c)). It is not surprising to find that the total contamination increases with decreasing explosion energy. For smaller explosion energies, smaller fractions of the ejecta are able to overcome the gravitational potential energy at the end of momentum exchange. Therefore, a high contamination of ∼1.2 × 10−2 M☉ is found in impact simulations with the lowest explosion energy of 0.8 × 1051 erg (W708_He01_r model, see Table 1).
Figure 16. (a) Total stripped mass as a function of the SN explosion energy (see Table 1). (b) Power-law fit of the dependence of total accreted ejecta masses (B1 = 0.005, μ1 = −2.133) on the SN explosion energy (Table 1). (c) Similar to (b), but for the kick velocity (B2 = 65.49, μ2 = 1.114). The star and cross symbols represent the results of the impact simulations. Lines show fitted linear (power-law) relations based on the numerical simulation results.
Download figure:
Standard image High-resolution image4.3.4. Decay of Unstable Isotopes
At the end of our simulations, the envelope of the surviving companion star is enriched by the heavy elements accreted from the low-expansion-velocity tail of the SN ejecta. In order to investigate whether the surviving companion stars would be expected to show observational overabundance signatures, we estimate the ratio of the bound Ni (or Fe) mass to the envelope He mass of a surviving companion (see Table 1) adopting the method of Pan et al. (2010). We also assume uniform mixing of the contaminants in the envelope. With two different companion models, the ratio of accreted Ni mass to the companion envelope He mass, MNi/MHe, is ∼2–4× 10−3, which corresponds to a value of (MNi/MHe)/(MNi/MH + He)☉ ≈ 24–48. At the same time MFe/MHe ∼ 4–9 × 10−3, which corresponds to (MFe/MHe)/(MFe/MH + He)☉ ≈ 2–6. Here, we use the solar composition of Lodders (2003) to obtain the corresponding value of (MNi/MH + He)☉ to compare with our simulation values.
However, the above results neglect the radioactive decay of unstable isotopes. Figure 17 shows that the captured SN-ejecta material contains several unstable isotopes (56Ni, 56Co, 57Co, 55Fe, etc.), although stable species are the primary components. The further decay of unstable isotopes changes the long timescale Fe (or Ni) abundances of the star. However, compared with the solar value of iron/nickel-to-hydrogen plus helium of Lodders (2003), our simulation values after the radioactive decays are still larger (see Figure 13), providing a possible way to identify a surviving companion star in SNRs by detecting its unusual chemical abundance. We note that our previous hydrodynamical simulations for WD+MS-like models showed that the amount of contamination of SN ejecta is ≲ 10−5 M☉ (which corresponds to a small number of ejecta particles). However, this contamination of ≲ 10−5 M☉ is too small to ensure whether it is a real contamination or not.
Figure 17. Details of mass distributions of stable and unstable isotopes of accreted iron-peak elements (Cr, Mn, Fe, Co and Ni, i.e., vertical gray range of Figure 13) in the impact simulations for the W7_He01 model.
Download figure:
Standard image High-resolution image4.3.5. Delayed Detonation Explosion Model
Our hydrodynamics simulations with a classical W7 model show that a surviving companion star in the WD+HE scenario can be significantly enriched by heavy elements of the innermost SN ejecta. However, the precise explosion mechanism of SNe Ia remains unclear. Different composition structures in various SN Ia explosion models might affect the abundance of captured heavy elements after the SN explosion.
To simply predict the effects of different explosion models, mass distributions of ejecta elements of a delayed detonation model (Seitenzahl et al. 2013) after radioactive decays of unstable isotopes are compared with those of the W7 model. Here, we use the "N100 model" of Seitenzahl et al. (2013) as an example realization of the delayed detonation mechanism of a SN Ia (see also Röpke et al. 2012). The detailed comparisons within different SN-ejecta velocities are shown in Figures 18 and 19. The delayed detonation mechanism in the SD scenario has been suggested to be the most promising way of producing observables in reasonable agreement with observations of normal SNe Ia (Khokhlov 1991). In Section 4.3, it is found that most of the captured heavy elements come from the innermost SN ejecta (see Figure 14). Therefore, we restrict the detailed comparisons in Figures 18 and 19 to SN-ejecta regions with an expansion velocity of ≲ 5000 km s−1.
Figure 18. Chemical composition of a delayed detonation model of "N100" (squares; Seitenzahl et al. 2013) and the W7 model (circles) after radioactive decays of unstable isotopes. Different panels show details of the composition for different ejecta regions of the inner 1000, 2000, 3000, 5000 km s−1. For example, the top (or bottom) panel shows the chemical composition of all ejecta material inside the spherical shell at ejecta velocity of 1000 km s−1 (or 5000 km s−1).
Download figure:
Standard image High-resolution imageFigure 19. Similar to Figure 18, but for different isotopes of selected elements from Ca to Zn. Squares are the delayed detonation model (i.e., N100 model) and circles are the W7 model.
Download figure:
Standard image High-resolution imageIn Figure 18, the inner ejecta of the "N100 model" show distinctly smaller masses of stable Ni, Co, Mn and Cr compared to those of the "W7 model," but basically similar stable Fe mass. Therefore, we can roughly expect that a surviving companion star may be less enhanced with Ni, Co, Mn and Cr due to the relatively ineffective enrichment if we use the N100 model instead of the W7 model to carry out the same impact hydrodynamics simulations. However, we do not expect the N100 model will lead to a surviving companion star with significantly different Fe abundance compared to a surviving companion impacted by W7 ejecta. Moreover, a significant amount of stable Si, Ca, S and Ar within 5000 km s−1 in the N100 model indicates that its surviving companion star might show an observable signature of Si, Ca, S and Ar enhancement (see Figure 18).
4.4. Indicators of a Surviving Companion Star
In case some SNe Ia originate from the WD+HE MCh scenario, our simulations indicate that surviving companion stars would show characteristic observational features due to contamination by SN ejecta (see Section 4.3). This may help to identify a surviving companion star even a long time after the SN explosion.
In our simulations, it is found that the kick velocity received by a companion is ∼58–67 km s−1. WMCH09 showed that the He companion has an orbital velocity of ∼300–500 km s−1 at the moment of the SN explosion. This indicates that a surviving companion star will have a high spatial velocity that is similar to its pre-explosion orbital velocity.
A small stripped mass (∼0.03–0.06 M☉) is insufficient to remove the total angular momentum of a He companion (only 13%–38% of initial angular momentum is lost from the star, see Figure 20). Therefore, we expect that He survivors would be rapid rotators (for a detailed discussion of post-impact rotation of surviving companion stars, see Liu et al. 2013; Pan et al. 2013). In WMCH09, it was shown that the pre-explosion rotational velocities of companion stars in the WD+HE MCh channel are 120–380 km s−1 assuming that the rotation of the companion star is phase-locked to its orbital motion due to tidal forces.
Figure 20. Temporal evolution of the total angular momentum of the companion star in the W7_He01_r (top panel) and W7_He02_r (bottom panel) models (see Table 1).
Download figure:
Standard image High-resolution imageAt the end of our simulations, about 0.028–0.056 M☉ of He-rich material are stripped off from the He companion stars. Full radiative transport calculations with the results of our hydrodynamics simulations are required to assess the possibility of detecting He lines in the nebular spectra of the modeled events.
After the SN impact, a surviving companion star dramatically puffs up due to the significant SN heating, and it would become a luminous He star near the SNR center while its equilibrium is reestablished during several centuries after the explosion (Pan et al. 2013). Moreover, it may be a rapidly rotating star with a high spatial velocity (see Pan et al. 2013).
One way to verify the WD+HE progenitor scenario is by identifying a corresponding surviving star in a SN remnant.
5. SUMMARY AND CONCLUSIONS
The primary goal of this work has been to investigate the interaction of SN Ia ejecta with the companion star within the WD+HE MCh explosion scenario. We mainly focused on whether or not a surviving companion shows an unusual abundance signature after the SN explosion. We have performed 3D hydrodynamics impact simulations employing the SPH code Stellar GADGET. The effect of the orbital motion and spin of the companion star were also taken into account. Two representative He companion models were obtained from 1D consistent binary evolution calculations with Eggleton's stellar evolution code, treating the mass loss of the donor star as RLOF. Our main conclusions are summarized as follows.
- 1.In the WD+HE MCh scenario, it is found that only ∼2%–5% of the initial companion mass can be stripped off due to the SN impact. The star receives a small kick velocity of ∼58–67 km s−1.
- 2.
- 3.The orbital motion and spin of a He companion star do not significantly affect the amount of unbound mass and kick velocity caused by the SN impact.
- 4.Our simulations predict that a surviving companion star in the WD+HE MCh channel moves with a high spatial velocity and should be a fast rotator after the SN explosion.
- 5.The He companion star is enriched by the heavy elements with low expansion velocity of the SN Ia ejecta. The total contamination is ≳ 10−3 M☉, providing a potential way to identify a survivor after the SN explosion.
- 6.The amount of contamination from SN Ia ejecta decreases with the increase of SN explosion energy and can be fitted with a power-law relation to a good approximation.
Our results are based on the standard SN Ia explosion model "W7" (Nomoto et al. 1984; Maeda et al. 2010). The comparison in Section 4.3.5 indicates that more comprehensive investigations with various state-of-the-art explosion models are needed to reliably predict whether the surviving companion star in the WD+HE MCh channel would show unusual abundances.
We thank U. Noebauer for very useful discussions. Z.W.L and Z.W.H thank the financial support from the MPG-CAS Joint Doctoral Promotion Program (DPP) and Max Planck Institute for Astrophysics (MPA). This work is supported by the National Basic Research Program of China (grant No. 2009CB824800), the National Natural Science Foundation of China (grant Nos. 11033008 and 11103072) and the Chinese Academy of Sciences (grant No. KJCX2-YW-T24). The work of F.K.R was supported by Deutsche Forschungsgemeinschaft (DFG) via the Emmy Noether Program (RO 3676/1-1) and by the ARCHES prize of the German Federal Ministry of Education and Research (BMBF). The work by K.M. is supported by World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan, and by Grant-in-Aid for Scientific Research for Young Scientists (23740141). S.T. is supported by the DFG through the Transregional Collaborative Research Centre "The Dark Universe" (TRR 33). The simulations were carried out at the Computing Center of the Max Planck Society, Garching, Germany.
Footnotes
- 8
In the SD scenario, a WD accretes and retains companion matter that carries angular momentum. As a consequence the WD spins with a short period which leads to an increase of the critical explosion mass. If the critical mass is higher than the actual mass of the WD, the SN explosion can only occur after the WD increases the spin period with a specific spin-down timescale (see Di Stefano et al. 2011; Justham 2011).
- 9
- 10
Note that we use the same power-law relation for different A/R2 (different companion models) to predict the unbound masses. However, it is found that different companion models would lead to different fitting parameters in SPH simulations (see Figure 7).
- Bloom J. S., Kasen D., Shen K. J. et al. 2012 ApJL 744 L17
- Chomiuk L., Soderberg A. M., Moe M. et al. 2012 ApJ 750 164
- Dewi J. D. M., Pols O. R., Savonije G. J. and van den Heuvel E. P. J. 2002 MNRAS 331 1027
- Dilday B., Howell D. A., Cenko S. B. et al. 2012 Sci 337 942
- Di Stefano R. and Kilic M. 2012 ApJ 759 56
- Di Stefano R., Voss R. and Claeys J. S. W. 2011 ApJL 738 L1
- Eggleton P. P. 1971 MNRAS 151 351
- Eggleton P. P. 1972 MNRAS 156 361
- Eggleton P. P. 1973 MNRAS 163 279
- Eggleton P. P. 1983 ApJ 268 368
- Fink M., Hillebrandt W. and Röpke F. K. 2007 A&A 476 1133
- Fink M., Röpke F. K., Hillebrandt W. et al. 2010 A&A 514 A53
- Foley R. J., Kromer M., Howie Marion G. et al. 2012 ApJL 753 L5
- Gamezo V. N., Khokhlov A. M. and Oran E. S. 2005 ApJ 623 337
- García-Senz D., Badenes C. and Serichol N. 2012 ApJ 745 75
- González Hernández J. I., Ruiz-Lapuente P., Filippenko A. V. et al. 2009 ApJ 691 1
- Hachisu I., Kato M. and Nomoto K. 1996 ApJL 470 L97
- Hachisu I., Kato M. and Nomoto K. 1999 ApJ 522 487
- Han Z. and Podsiadlowski P. 2004 MNRAS 350 1301
- Hillebrandt W., Kromer M., Röpke F. K. and Ruiter A. J. 2013 FrPhy 8 116
- Hillebrandt W. and Niemeyer J. C. 2000 ARA&A 38 191
- Horesh A., Kulkarni S. R., Fox D. B. et al. 2012 ApJ 746 21
- Iben I. Jr. and Tutukov A. V. 1984 ApJS 54 335
- Justham S. 2011 ApJL 730 L34
- Kasen D., Nugent P., Thomas R. C. and Wang L. 2004 ApJ 610 876
- Kato M. and Hachisu I. 2004 ApJL 613 L129
- Kerzendorf W. E., Yong D., Schmidt B. P. et al. 2012 arXiv:1210.2713
- Khokhlov A. M. 1991 A&A 245 114
- Landau L. D. and Lifshitz E. M. 1971 The Classical Theory of Fields (Oxford: Pergamon)
- Lentz E. J., Baron E., Branch D. and Hauschildt P. H. 2001 ApJ 557 266
- Leonard D. C. 2007 ApJ 670 1275
- Li W., Bloom J. S., Podsiadlowski P. et al. 2011 Natur 480 348
- Liu Z.-W., Pakmor R., Roepke F. K. et al. 2013 A&A 554 A109
- Liu Z. W., Pakmor R., Röpke F. K. et al. 2012 A&A 548 A2
- Lodders K. 2003 ApJ 591 1220
- Maeda K., Benetti S., Stritzinger M. et al. 2010 Natur 466 82
- Maoz D. and Badenes C. 2010 MNRAS 407 1314
- Maoz D. and Mannucci F. 2012 PASA 29 447
- Maoz D., Sharon K. and Gal-Yam A. 2010 ApJ 722 1879
- Marietta E., Burrows A. and Fryxell B. 2000 ApJS 128 615
- Nomoto K. 1982 ApJ 253 798
- Nomoto K. and Iben I. Jr. 1985 ApJ 297 531
- Nomoto K., Saio H., Kato M. and Hachisu I. 2007 ApJ 663 1269
- Nomoto K., Thielemann F.-K. and Yokoi K. 1984 ApJ 286 644
- Nugent P. E., Sullivan M., Cenko S. B. et al. 2011 Natur 480 344
- Pakmor R., Edelmann P., Röpke F. K. and Hillebrandt W. 2012a MNRAS 424 2222
- Pakmor R., Hachinger S., Röpke F. K. and Hillebrandt W. 2011 A&A 528 A117
- Pakmor R., Kromer M., Röpke F. K. et al. 2010 Natur 463 61
- Pakmor R., Kromer M. and Taubenberger S. 2013 ApJL 770 L8
- Pakmor R., Kromer M., Taubenberger S. et al. 2012b ApJL 747 L10
- Pakmor R., Röpke F. K., Weiss A. and Hillebrandt W. 2008 A&A 489 943
- Pan K.-C., Ricker P. and Taam R. 2013 ApJ 773 49
- Pan K.-C., Ricker P. M. and Taam R. E. 2010 ApJ 715 78
- Pan K.-C., Ricker P. M. and Taam R. E. 2012 ApJ 750 151
- Patat F., Chandra P., Chevalier R. et al. 2007 Sci 317 924
- Perlmutter S., Aldering G., Goldhaber G. et al. 1999 ApJ 517 565
- Price D. J. 2007 PASA 24 159
- Riess A. G., Filippenko A. V., Challis P. et al. 1998 AJ 116 1009
- Röpke F. K., Hillebrandt W., Schmidt W. et al. 2007 ApJ 668 1132
- Röpke F. K., Kromer M., Seitenzahl I. R. et al. 2012 ApJL 750 L19
- Ruiter A. J., Belczynski K. and Fryer C. 2009 ApJ 699 2026
- Schaefer B. E. and Pagnotta A. 2012 Natur 481 164
- Schmidt B. P., Suntzeff N. B., Phillips M. M. et al. 1998 ApJ 507 46
- Seitenzahl I. R., Ciaraldi-Schoolmann F., Röpke F. K. et al. 2013 MNRAS 429 1156
- Shappee B. J., Stanek K. Z., Pogge R. W. and Garnavich P. M. 2013 ApJL 762 L5
- Shen K. J., Guillochon J. and Foley R. J. 2013 ApJL 770 L35
- Springel V. 2005 MNRAS 364 1105
- Sternberg A., Gal-Yam A., Simon J. D. et al. 2011 Sci 333 856
- Timmes F. X., Woosley S. E. and Taam R. E. 1994 ApJ 420 348
- Wang B., Chen X., Meng X. and Han Z. 2009a ApJ 701 1540
- Wang B. and Han Z. 2010 A&A 515 A88
- Wang B., Li X.-D. and Han Z.-W. 2010 MNRAS 401 2729
- Wang B., Meng X., Chen X. and Han Z. 2009b MNRAS 395 847
- Wang L. and Wheeler J. C. 2008 ARA&A 46 433
- Webbink R. F. 1984 ApJ 277 355
- Whelan J. and Iben I. Jr. 1973 ApJ 186 1007
- Woosley S. E. and Kasen D. 2011 ApJ 734 38
- Woosley S. E., Taam R. E. and Weaver T. A. 1986 ApJ 301 601
- Woosley S. E. and Weaver T. A. 1994 ApJ 423 371