ABSTRACT
The helium-merger gamma-ray burst (GRB) progenitor is produced by the rapid accretion onto a compact remnant (neutron star or black hole) when it undergoes a common envelope inspiral with its companion's helium core. This merger phase produces a very distinct environment around these outbursts and recent observations suggest that, in some cases, we are detecting the signatures of the past merger in the GRB afterglow. These observations allow us, for the first time, to study the specific features of the helium-merger progenitor. In this paper, we couple population synthesis calculations to our current understanding of GRB engines and common envelope evolution to make observational predictions for the helium-merger GRB population. Many mergers do not produce GRB outbursts and we discuss the implications of these mergers with the broader population of astrophysical transients.
1. INTRODUCTION
The black hole accretion disk gamma-ray burst (GRB) engine has become standard for long- and short-duration GRBs alike (Popham et al. 1999). For long-duration bursts, the most commonly invoked progenitor is the collapse of a rapidly rotating massive star down to a black hole. But achieving the high angular momentum needed to produce a disk around the newly formed black hole has proved problematic and a number of progenitors have been invoked to provide these high angular momentum profiles (Fryer & Woosley 1998; Fryer et al. 1999, 2007b; Yoon & Langer 2005; Woosley & Heger 2006; Belczynski et al. 2007; Podsiadlowski & Ivanova 2003; Portegies-Zwart et al. 2005; Bogomazov et al. 2007; van den Heuvel & Yoon 2007; Podsiadlowski et al. 2010).
One such model invokes the merger of a compact remnant with its companion. As the compact remnant spirals into the center of the helium core of an evolved companion, the accretion rate can exceed 0.01 M☉ s−1, enough to power a strong GRB (Fryer & Woosley 1998). The basic idea behind this model is that as the compact remnant spirals into its companion, the orbital energy lost both spins up the helium core and ejects the hydrogen envelope. If the compact remnant is a neutron star, the rapid accretion in the inspiral is likely to cause it to collapse to a black hole. In this manner, the helium-merger model provides a natural way to ensure enough angular momentum to form a disk around a central black hole.
Simulations by Zhang & Fryer (2001) showed that the inspiral would produce both the high angular momenta and accretion rates needed to create a black hole accretion disk engine. Although there is some concern that helium mergers produce disks with too much angular momentum (DiMatteo et al. 2002), current analyses find that this angular momentum is appropriate for accretion disk engines (Komissarov & Barkov 2009; Barkov & Komissarov 2011). The helium-merger model predicts a feature that may be observable in the resultant explosion: the existence of a shell (or torus) of merger-ejecta surrounding the burst.
Initially, Fryer & Woosley (1998) believed the helium-merger model would be difficult to distinguish from normal GRBs because the ejecta from the common envelope phase would lie along the orbital plane (the same plane as the disk) and there would be very little interaction between the ejecta and the GRB jet. This picture changed with the observation of GRB 101225A, the so-called Christmas Burst (Thöne et al. 2011). This burst exhibited blackbody emission arguing for a compact progenitor (∼1011 cm) followed by a second blackbody component with a characteristic radius of ∼1014 cm. Simulations of the jet interactions with more realistic common envelope ejecta profiles (also based on recent simulations) found that the helium-merger model could produce the thermal emission in this burst (Thöne et al. 2011). The X-ray Flare 060218 (and perhaps a few other low-redshift bursts) may have similar characteristics, suggesting that these helium-merger events may be identifiable after all.
To truly compare these systems to the observed data, we must understand the entire population of compact merger events. In this paper, we undertake a series of population synthesis models studying the characteristics of compact merger events. Section 2 describes the population synthesis calculations and presents the basic results of these calculations: rates and characteristics of merging systems. In Section 3, we analyze these results, making predictions for luminosities and ejecta positions for merger outbursts. We conclude with a discussion of the potential observational outcomes of this black hole accretion disk progenitor.
2. NEUTRON STAR/BLACK HOLE MERGER POPULATIONS
2.1. Population Synthesis Calculations
To study the helium-merger progenitor, we use the population synthesis code StarTrack to calculate the numbers and properties of merging systems. The full description of the code can be found in Belczynski et al. (2002, 2008). The code utilizes a set of stellar models (Hurley et al. 2000; slightly modified from its original version) that allow for the evolution of stars at different metallicities. The model for compact object formation adopted in the code has been significantly revised (Dominik et al. 2012). During core collapse, fallback and direct black hole formation is now accounted for (Fryer & Kalogera 2001) and the newly born objects receive natal kicks (Hobbs et al. 2005). The formation of low-mass neutron stars through electron capture supernovae is also accounted for (e.g., Podsiadlowski et al. 2004). Binary interactions are treated in detail, and the various physical processes have been calibrated using either the results of detailed evolutionary calculations (e.g., Wellstein & Langer 1999 for mass transfer sequences), or specific sets of observations (e.g., Levine et al. 2000 for tidal interactions). The mass loss prescription for winds in massive stars, the stellar binding energy used in common envelope evolution, and the compact remnant mass formation prescription have all been updated (Dominik et al. 2012).
2.2. Rates
In each calculation, we have evolved N = 2 × 105 binaries with the primary mass range M1 = 5–150 M☉ and secondary mass range M1 = 0.08–150 M☉. The stars were evolved with solar metallicity (Z = 0.02). Each binary system is initiated by four parameters, which are assumed to be independent: the primary mass M1 (the initially more massive component), the mass ratio q = (M2/M1), where M2 is the mass of the secondary, the semimajor axis a of the orbit, and the orbital eccentricity e.
For both single stars and binary system primaries, we use the initial mass function adopted from Kroupa & Weidner (2003),
where parameter αimf = 2.35–3.2: for our "standard" models, we use an intermediate value of 2.7.
We adopt a flat mass ratio distribution that is consistent with the recent observational results (Kobulnicky & Fryer 2007; Kobulnicky et al. 2012),
in the range q = 0–1. Given value of the primary mass and the mass ratio, we obtain the mass of the secondary M2 = qM1.
The distribution of the initial binary separations is assumed to be flat in the logarithm (Abt 1983),
where a ranges from a minimum value, such that the primary fills at maximum 50% of its Roche lobe at ZAMS, up to 105 R☉.
We adopt the thermal-equilibrium eccentricity distribution for initial binaries,
in the range e = 0–1 (e.g., Heggie 1975; Duquennoy & Mayor 1991).
We have evolved only binaries massive enough to potentially produce at least one compact object and therefore produce a helium merger. If we extend the evolved population to include the entire mass spectrum and if we include single stars as well (with binary fraction fbi = 0.5), each calculation with αimf = 2.7 would correspond to a stellar mass formed in a starburst mass of 4.5 × 107 M☉.
As one might expect, the evolution of the binary in the common envelope is critical for the He-merger population. Within these basic initial conditions for binary populations, we conduct six different calculations, mostly focusing on the behavior in common envelope (Table 1). We vary the treatment for the binding energy of the star (λ) and the survivability in of the merger if it occurs when the star is in the Hertzsprung gap (for more details, see Dominik et al. 2012). We study both solar and 10% solar metallicity models.
Table 1. Population Synthesis Models
| Model | λCE | Hertzsprung Gap | Metallicity |
|---|---|---|---|
| Fatea | |||
| Model 1 | Physical λb | CE formulae | Solar |
| Model 2 | 3×physical λ | CE formulae | Solar |
| Model 3 | Constant λ = 1 | CE formulae | Solar |
| Model 4 | Physical λ | HG always merges | Solar |
| Model 5 | Physical λ | CE formulae | 10% solar |
| Model 6 | Physical λ | HG always merges | 10% solar |
Notes. aStars in the Hertzsprung gap do not have strong entropy gradients dividing the helium core and hydrogen envelope. Without these sharp gradients, every CE phase will proceed through the merger with the helium core. We choose two fates: ignore this entropy argument ("CE formulae") or include this effect and assume that Hertzsprung gap CE scenarios lead to a merged system ("HG always merges"). For more details, see Dominik et al. (2012). bPhysical λ corresponds to the Xu & Li (2010) used by Dominik et al. (2012).
Download table as: ASCIITypeset image
Table 2 shows the total number of mergers produced using 2 × 105 binaries. The rates are divided into three categories: main-sequence merger, mergers with small helium core masses, and mergers with large helium core masses. In each category we include mergers in which the compact object can be either a neutron star or a black hole. These rates correspond to the rate per 4.5 × 107 M☉ of star forming mass. The number in parentheses show the number of the total systems produced because of neutron star kicks. Although kicks produce many of the merging systems (30%), kick-induced mergers account for a smaller fraction (∼10%) of low-mass helium core mergers and almost none (<1%) of the massive helium mergers believed to be GRBs.
Table 2. Merger Rates I (per 4.5 × 107 M☉)
| Model | He-merger Rate | He-merger Rate | Main-sequence |
|---|---|---|---|
| (MHe < 4.0 M☉) | (MHe > 4.0 M☉) | Merger Rate | |
| Model 1 | 718(110)a | 939(0) | 579(175) |
| Model 2 | 507(35) | 406(0) | 1267(411) |
| Model 3 | 967(94) | 227(3) | 1566(478) |
| Model 4 | 929(24) | 1020(2) | 580(175) |
| Model 5 | 1505(1) | 2019(9) | 796(249) |
| Model 6 | 1790(1) | 3033(6) | 755(262) |
Note. aThe left number in each column denotes the total number of systems produced in each category. The numbers in parentheses show the number of these systems formed due to neutron star and black hole kicks.
Download table as: ASCIITypeset image
These rates can be folded with any desired star formation history to give an actual time-dependent helium-merger rate in a given galaxy. Table 3 shows the merger rate per Myr in a Milky-Way-massed galaxy as well as the volumetric (Gpc−3 yr−1) rate assuming a star formation rate equivalent to 10 million Milky Way galaxies per Gpc3. If we wish to compare to GRBs, a rough estimate of the rates should include a combination of solar and low metallicity rates (e.g., 50% each of Models 1 and 5 or 50% each of Models 4 and 6). The resultant rates predicted are 629, 857 Gpc−3 yr−1 for respective models assuming normal CE formulae for Hertzsprung gap mergers versus immediate mergers for these Hertzsprung gap mergers.
Table 3. Merger Rates II (Myr−1, Gpc−3 yr−1)
| Model | He-merger Rate | He-merger Rate | Main-sequence |
|---|---|---|---|
| (MHe < 4.0 M☉) | (MHe > 4.0 M☉) | Merger Rate | |
| Model 1 | 30.8(308.2)a | 40.3(403.0) | 24.9(248.5) |
| Model 2 | 22.0(220.3) | 17.6(176.4) | 55.0(550.5) |
| Model 3 | 43.2(431.5) | 10.1(101.3) | 69.9(69.9) |
| Model 4 | 39.9(399.2) | 43.8(438.3) | 24.9(249.3) |
| Model 5 | 63.7(636.7) | 85.4(854.2) | 33.7(336.8) |
| Model 6 | 75.2(752.4) | 127.5(1274.8) | 31.7(317.3) |
Note. aThe left number in each column denotes a rate per Milky-Way-massed galaxy (Myr−1) assuming a 1.95 M☉ yr−1 star formation rate. The numbers in parentheses show volumetric rate (Gpc−3 yr−1).
Download table as: ASCIITypeset image
The Fryer et al. (1999) Galactic rate for their standard model is 39 Myr−1, very close to our rate of high-mass helium cores. Such high rates mean that even if only 10% of these systems produce GRB jets, they can explain a large fraction of the long-duration GRB rates. Indeed, He-mergers may be the source of the large, relatively hidden, low-luminosity long-duration GRB population (Liang et al. 2007). The low-mass helium star merger and main-sequence merger rate is not significantly higher and, assuming that these mergers produce peculiar supernovae, they can account for no more than 1% of all core-collapse supernovae.
Like most of the proposed long-duration GRB progenitors, He-mergers will closely trace star formation. The delay time from star formation to merged event is limited to the stellar evolution time (in the He-merger case, it is the stellar evolution time of the companion star). For massive helium mergers, the merger occurs within 20 Myr of the initial star formation time (for main-sequence star mergers, the distribution can extend to 100 Myr).
2.3. Mass and Orbital Separation Distributions
Our populations demonstrate that compact remnant mergers can occur for a wide range of star characteristics: mass, evolutionary phase, and, hence, orbital separation at the time of the merger. In Section 3, we will use these characteristics to determine observable features of these mergers. Before we do so, let us review the characteristics of these populations.
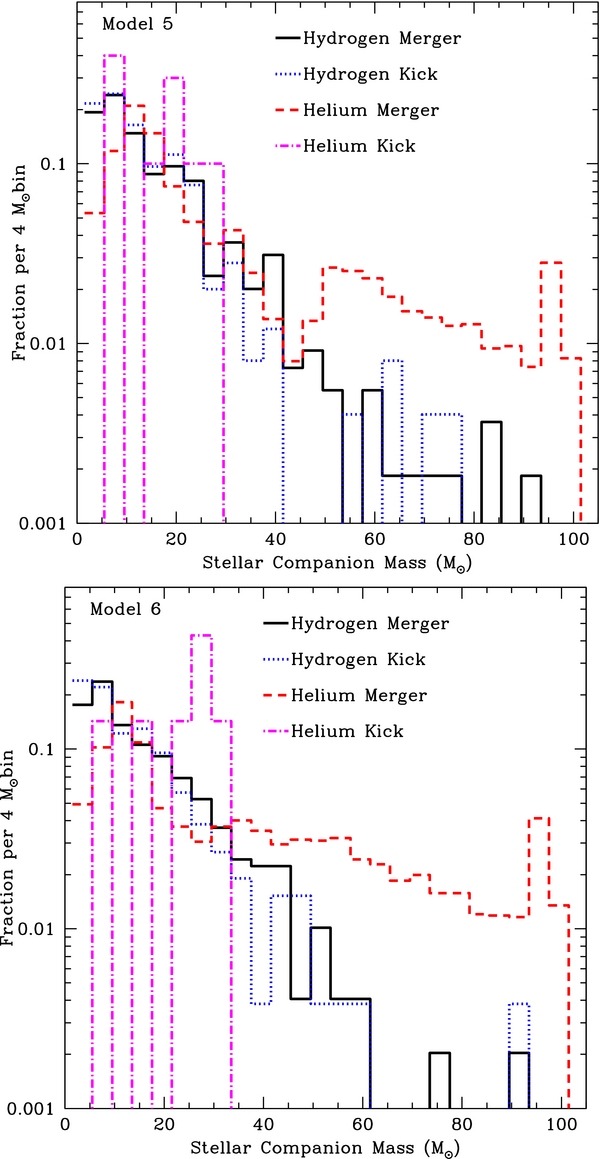
Figures 1 and 2 show the distribution of companion masses for four different merger populations: those with hydrogen cores merging through mass transfer, those with hydrogen cores merging when the compact remnant is kicked into the companion, those with helium cores merging through mass transfer, and those with helium cores merging when the compact remnant is kicked into the companion. As we might expect with our steep initial mass function, the companion masses are peaked to lower mass (below 20 M☉). However, the distribution is broad, extending beyond 60 M☉. He-merging systems have a secondary peak at higher masses and the most massive helium cores will come from this peak. For low-metallicity stars, this secondary peak occurs nearly at 90 M☉.
Figure 1. Companion star mass distribution for four different populations: those with hydrogen cores merging through mass transfer, those with hydrogen cores merging when the compact remnant is kicked into the companion, those with helium cores merging through a common envelope phase, and those with helium cores merging when the compact remnant is kicked into the companion. Except for helium-merger systems (which have companion masses ranging up to 60 M☉, often with a secondary peak at these high masses), most of the systems have companion masses peaking strongly at low masses.
Download figure:
Standard image High-resolution imageFigure 2. Companion star mass distribution for four different populations (see Figure 1). Note that for low metallicity systems, the helium-merger population has a much broader high-mass tail, producing mergers of neutron stars or black holes with stars in excess of 90 M☉.
Download figure:
Standard image High-resolution imageSimilarly, the distribution of companion radii is extremely broad (Figure 3). As expected, the evolved stars (with helium cores) can be much larger (up beyond 5 AU). The helium core sizes tend to lie in a narrow range between 0.5 and 3 R☉.
Figure 3. Companion star radius distribution for four different populations in Figure 1. The evolved stars (with helium cores) have much higher radii (up above 5 AU). Because there is very little variation between models, we show only four of our models.
Download figure:
Standard image High-resolution imageThe wide variation in these systems will produce a wide variation in the observational features of these explosions.
3. OBSERVABLE PROPERTIES
The characteristics of the compact binaries (companion masses, evolutionary phases, radii, and orbital separations) allow us to estimate both the explosion luminosities and spectral features.
3.1. Luminosities
For explosion luminosities, we will divide the discussion into two categories based on the accretion rate. If the system has a massive helium core (>4 M☉), the accretion is sufficient to power a strong black hole accretion disk engine discussed in classical GRBs. In these cases, even the neutrino-annihilation powered engine may be strong. These high accretion-rate systems fit the classic helium-merger model proposed by Fryer & Woosley (1998). We then study low-mass helium core and hydrogen core systems.
3.1.1. Massive Helium-core Merger: GRB-like
Our population synthesis models predict a wide set of merging systems involving a compact remnant (neutron star or black hole) with its companion. As we showed in Section 2.2, ∼10%–50% of these are mergers with evolved stars with helium core masses above 4 M☉. With a rate of 10–120 Myr−1, mergers with massive helium cores can make up a significant fraction of our GRB population. In this section, we use our current understanding of disk-engine models to predict explosion luminosities from the helium core mass distribution.
Zhang & Fryer (2001) studied the accretion onto a neutron star during an inspiral. They found that the more massive the helium core, the higher the accretion rate (and, ultimately, the more energetic GRB explosion). The neutron star will quickly accrete enough material to form a black hole and, unless an outburst is caused during this collapse, the neutron star and black hole systems may be difficult to distinguish. Our population synthesis models provide us with the distributions of helium core masses at the onset of the merger is shown in Figure 4. Although the helium core masses peak at low masses, the distribution of helium core masses for solar metallicity models extends beyond 25 M☉ and roughly half of the systems have helium cores with masses above 4 M☉. At low metallicities, the maximum helium core mass extends to 45 M☉.
Figure 4. Mass distribution of helium cores in our population of He-mergers. The two largest peaks exist for low-mass helium cores: 1.4 and 3.4 M☉. However, the distribution is widespread (half of all merging systems involve helium cores with masses above 4 M☉).
Download figure:
Standard image High-resolution imageWe can estimate the accretion rate onto the compact remnant ():
where tfree-fall is the free-fall timescale, MHe and RHe are the helium core mass and radius respectively, Mrem is the compact remnant mass, and G is the gravitational constant (55%–95% of our remnants are neutron stars, most initially with a mass 1.4 M☉ or less). The accretion rate is less than the typical free-fall time because the material has thermal pressure and considerable angular momentum. To account for this, we include an efficiency parameter η. Fitting to the Zhang & Fryer (2001) results, we find the value of η to be roughly 15%.
By using the helium core radii as a function of mass from the Woosley et al. (2002) pre-collapse helium cores, we derive an accretion rate as a function of helium core mass, shown in Figure 5. These helium cores are evolved (at collapse), but their radii are not too different from the unevolved cores used by Zhang & Fryer (2001). This accretion rate is fairly well fit by a two-part power law:
For helium cores with masses below 4 M☉, the accretion rate drops rapidly. These low-mass cores are less likely to drive strong explosions, and for the purposes of our discussion of helium mergers, we will focus on those helium cores with masses above 4 M☉.
Figure 5. Average accretion rate as a function of helium core mass. The dots show the results using the helium cores from the Woosley et al. (2002) models. The accretion rate data is fit by a two-piece power law of the helium core mass. Below 4 M☉, the power increases dramatically, driving the accretion rate down significantly as the helium core mass decreases.
Download figure:
Standard image High-resolution imageZhang & Fryer (2001) estimated the explosion luminosity as a function of accretion rate for a helium-merger GRB assuming both the Blandford–Znajek (Blandford & Znajek 1977) and neutrino annihilation mechanisms. For neutrino annihilation, we use the formula from Zhang & Fryer (2001):
where arem ≡ (Jremc)/(GM2rem), Jrem is the angular momentum of the remnant, and c is the speed of light. Values of arem for these mergers tend to lie in the range of 0.75–0.95. We will assume 0.9 for our estimates. This estimate assumes a roughly 3 M☉ black hole which, for the purposes of this study, is appropriate. However, other formulae exist that will produce different energy distributions, e.g., Zalamea & Beloborodov (2011). Our prescription produces a broader energy distribution than Zalamea & Beloborodov (2011) and, to demonstrate the range of energy distributions, we will focus on these formulae. However, one should bear in mind that the distribution of neutrino annihilation outbursts may be more narrow than predicted by our results.
The comparable equation for Blandford–Znajek emission is (Popham et al. 1999):
where Bmag is the magnetic field strength. As with Zhang & Fryer (2001), we will assume the magnetic energy density is equal to the kinetic energy density:
where we have approximated the density (ρ) and velocity (v) of the material using the values at the event horizon: rg = 2GMrem/c2. Again, we set arem to 0.9 for our estimates. The corresponding luminosity for both these models as a function of helium core mass is shown in Figure 6. Neutrino annihilation is much more sensitive to the helium core mass and leads to a broader spread of explosion energies. If neutrino cooling is not important, our magnetic-field formula overestimates the luminosity (Kawanaka et al. 2012). There may be a tail of low-luminosity GRBs from a magnetic field engine as well, causing a broader spread in energies.
Figure 6. Luminosity vs. helium core mass for our two power sources: neutrino annihilation () and Blandford–Znajek emission (LBZ). The stronger dependence of neutrino annihilation on the density and temperature (and hence accretion rate) means that the luminosity from neutrino annihilation is extremely sensitive to the helium core mass.
Download figure:
Standard image High-resolution imageThese formulae allow us to estimate the luminosity of the outburst from our helium-merger population. The distributions for both the neutrino annihilation and Blandford–Znajek models are shown in Figure 7. As expected, the sensitivity of the neutrino annihilation emission model leads to a broad spectrum of explosion luminosities. Our simplified Blandford Znajek model predicts a relatively narrow range of luminosities from 1050 to 1052 erg s−1.
Figure 7. Distribution of luminosities from the helium mergers from our population synthesis calculations. The neutrino annihilation model's strong sensitivity on the helium core mass leads to a broad distribution in the explosion energies.
Download figure:
Standard image High-resolution imageThe merger process ejects the hydrogen atmosphere of the star in a shell of material with a density enhancement along the orbital plane. It was this shell that Thöne et al. (2011) exploited to explain the peculiar features of the Christmas burst. They argued that interactions of the jet with this shell produced the late-time, large radius blackbody emission. We estimate the outer extent of this shell using the same analysis of Thöne et al. (2011): assume the inspiral occurs in ∼3 orbits and the material ejected in this common envelope phase moves outward at the escape velocity over these 3 orbits. Although these two assumptions are not strictly true, we cannot yet model this process exactly (e.g., Passy et al. 2012; Ivanova et al. 2012). These assumptions approximate the ultimate result within a factor of two in most cases. Figure 8 shows the distribution of shell positions for our He-merger populations calculated using these assumptions.
Figure 8. Distribution of shell positions of the massive He-mergers derived from our population synthesis models.
Download figure:
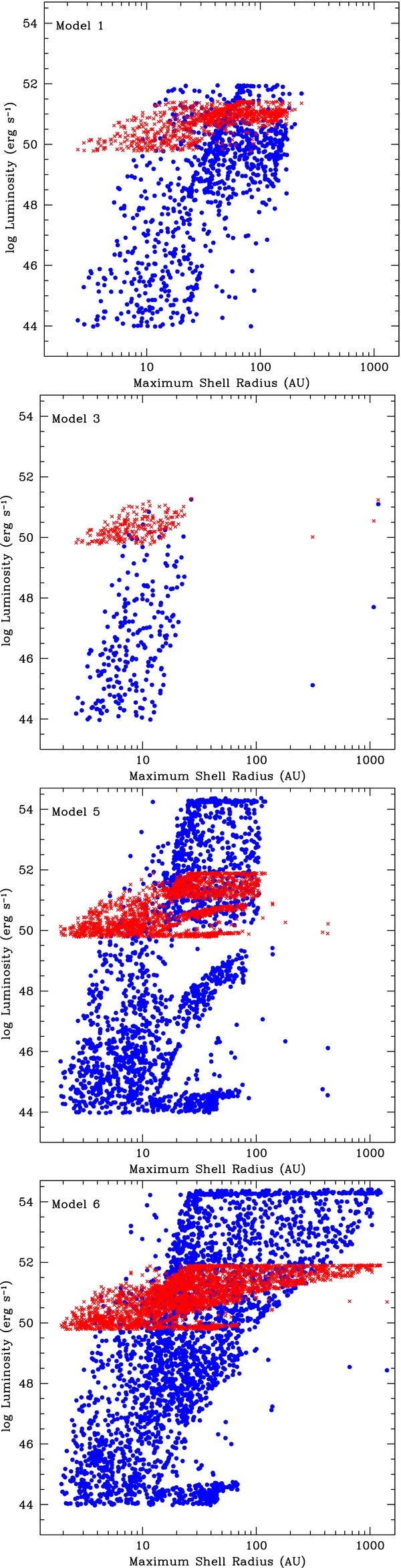
Standard image High-resolution imageOur population helium mergers predicts a range of luminosities versus maximum shell radii (Figure 9). There is considerable scatter in the relationship between the outer shell radii and luminosity. But there is a trend that the most luminous explosions have the furthest shell locations.
Figure 9. Luminosities vs. outer shell radii for our helium-merger population. Our Blandford–Znajek, magnetic field, engine (crosses) tends to produce stronger explosions in general, but the strongest explosion energies arise from our neutrino annihilation model (circles). The strongest energies tend to have the widest separations, but there is considerable scatter in the maximum radius–luminosity relation.
Download figure:
Standard image High-resolution image3.1.2. Supernova-like Explosions: Low-mass Helium Cores and Main-sequence Mergers
If the compact object merges with a lower-mass helium core or a main-sequence star, the accretion rate onto the remnant will be much lower. For these systems, the black hole accretion disk engine is unlikely to be valid and it is more difficult to produce even a rough estimate of the explosion energy.
Before the common envelope phase, many of our systems are likely to be X-ray binaries (Belczynski et al. 2013). At the onset of the common envelope phase, the X-ray binary can evolve, becoming more powerful. The system may even begin to produce strong jets. These so-called micro-quasars have been observed in numerous systems (see Mirabel 2007 for a review).
What happens as the compact remnant spirals into its companion is more difficult to determine. In these mergers, the accretion rate is slow enough that the neutron star may not initially collapse to form a black hole. The accretion rate remains high enough that any neutron star magnetic field is likely to be buried. Even without magnetic fields, these accretion events can produce explosions on par with normal supernova (Fryer et al. 2006a; Fryer 2009).
Presumably, once the compact remnant collapses to a black hole, the accretion disk will produce a jet. In these hydrogen or low-mass helium cores, the accretion rate is insufficient for the neutrino annihilation model to work, but we still do not understand the black hole accretion disk mechanism well enough to predict whether such systems will produce jets with explosions at GRB levels or at sub-supernova levels.
3.2. Nucleosynthetic Yields
Two sites have been identified in long-duration GRBs to produce 56Ni: explosive nucleosynthesis in the shock (this shock burning is what produces the 56Ni in supernovae), or disk-wind nucleosynthesis (Surman et al. 2006, 2011).
Explosive nucleosynthesis produces 56Ni in the silicon and oxygen layers of an evolved core in normal supernovae or classic collapsars. Without an evolved core, it is difficult for the helium-merger model to produce significant 56Ni from shock interactions. Unless considerable material is processed and ejected in the disk, very little 56Ni is produced. Like the fallback GRBs discussed in Fryer et al. (2007a), these GRBs could produce low-nickel yield outbursts. Although this may not affect the peak of the light curve (in most of these systems, shock heating dominates the light curve at peak; Fryer et al. 2007a, 2009), it does mean that if explosive nucleosynthesis is the dominant source of 56Ni, these explosions will not have typical 56Ni decay tails at late times.
However, if disk winds dominate the 56Ni production, the nucleosynthetic yields of GRB-like He-mergers will be indistinguishable from collapsar long-duration GRBs.
3.3. Spectra
Contamination from the ejected hydrogen envelope is the strongest constraint for He-mergers. However, the hydrogen distribution in the helium-merger model is different from typical stellar envelopes. Even though the hydrogen remains within 1015 cm of the central engine, the distribution is very asymmetric. Passy et al. (2012) found that 90% of the mass ejected was distributed within 30° of the equator. It is more difficult to accurately describe the distribution of the remaining 10%. Combined with the fact that the explosion is also asymmetric, it is possible to sweep up very little mass.
How low must the swept-up hydrogen mass be? For symmetric explosions, Hachinger et al. (2012) found that roughly 0.1 solar masses of hydrogen could be hidden in the explosion. For asymmetric supernovae, this number may be a bit greater. This would require only 1%–2% of the stellar-envelope hydrogen remain within the supernova opening angle (perhaps within 30° of the rotation axis).
Either the supernova explosion itself must be asymmetric (e.g., a jet-like explosion), or it must become asymmetric as it expands through the star. The He-merger leaves behind a highly asymmetric density profile, with much lower densities along the orbital angular momentum axis. This density asymmetry is both in the helium shell and the hydrogen ejecta. To determine how well the low density funnel can focus the explosion, we have simulated using the SNSPH code (Fryer et al. 2006b; Ellinger et al. 2012) a 5.6 × 1051 erg explosion focused in a 30° wedge of a 25 M☉ where the density in this wedge is lowered by a factor of 100. The explosion at 0.47 d is shown in Figure 10. In this calculation, roughly 0.0001 M☉ of hydrogen is swept up in the explosion. This hydrogen mass is 3 orders of magnitude lower than typical type IIb supernovae and can easily be hidden in the spectra. This supernova would produce a Ib/c supernova.
Figure 10. SNSPH particle positions for a 5.6 × 1051 erg explosion focused in a 30° wedge of a 25 M☉. The density in this wedge is lowered by a factor of 100 with respect to the rest of the star. The shading shows the different chemical abundances with black denoting hydrogen and lighter shades showing helium, carbon, oxygen and silicon abundances.
Download figure:
Standard image High-resolution imageHow much hydrogen is swept up (and whether or not we will see it in the explosion) depends upon the details of the density profile set by the merger ejecta and the asymmetry in the explosion. For GRB-like jets expected from massive helium-core mergers, the amount swept up should not be detectable. But for main-sequence stars, the explosion may not be so jet-like, and the amount of hydrogen in the explosion could be large.
Finally, like with most collapsar progenitors, the helium in the ejecta must either be burned to C/O in the shock, or must be hidden in the supernova spectra. This remains one of the primary open problems with the Collapsar GRB model as well (Fryer et al. 2007b).
4. COMPARISON TO TRANSIENT POPULATIONS
We have calculated the formation rates of the helium-merger scenarios, the extent of the surrounding hydrogen shells, and the expected accretion rates onto the compact remnant after these mergers. The rates of our massive He-core explosions are on par with the long-duration GRB rate, and the total He-merger and main-sequence merger rate is roughly 1% the supernova rate. In particular, our theoretical massive He-core merger rates for solar metallicity (∼100–400 Gpc−3 yr−1; see Table 3) are consistent with empirically estimated rates based on the Galactic high-mass X-ray binaries: ∼60–180 Gpc−3 yr−1 (Belczynski et al. 2013). For massive (>4 M☉) helium cores, energies can be as high as any black hole accretion disk model. These models produce a range of hydrogen shells surrounding the star at 1–100 AU. But to truly understand the nature of the explosions of these mergers requires a better understanding of the black hole accretion disk engine. In this section, we review some of the possible outcomes of these objects.
4.1. He-mergers and GRBs
We have shown that for a subclass of merging systems, the accretion rates onto the black hole can provide the energetics needed to drive a GRB outburst. In addition, the rate of this subclass is sufficient to explain GRBs. But can these mergers explain the full suite of GRB diagnostics?
Thöne et al. (2011) argued that these mergers could fit a very peculiar subset of GRBs with an unusual optical counterpart. But can helium mergers explain a broader set of GRBs? One of the key constraints of long-duration GRB progenitors is the association of a particular subtype of supernova (Type Ic) with GRBs. The 56Ni estimates for these supernovae tend to be higher than typical Ib/c supernovae with broader line profiles suggesting asymmetric explosions. Is it possible for the He-merger progenitor to reproduce this supernova/GRB association?
If the helium-merger model cannot satisfy these requirements, it may be limited to explaining only a few odd GRBs such as the Christmas burst. The shell position in the Christmas Burst (∼10 AU) is characteristic of our He-merger predictions, but we expect a range shell positions from 1 to 100 AU.
One feature of the helium-merger model is that it typically has an order of magnitude higher angular momenta than the collapsar model. This leads to larger accretion disks with larger accretion times, although for the typical specific angular momenta of 1018 cm2 s−1 Zhang & Fryer (2001), the accretion disk remains with 109 cm and may not produce drastically different characteristics than the Collapsar model. The higher accretion rate may yield weaker explosions and these mergers may explain the potentially large population of low-luminosity GRBs (Liang et al. 2007). Unfortunately, at this point, our lack of understanding of the GRB engine makes it difficult to tie this difference in disk size to an observation. But as we better understand the engine, this difference may lead to observable consequences.
4.2. Peculiar Supernovae
If the explosion is asymmetric but there is too much hydrogen within the supernova explosion to produce a relativistic jet, helium mergers may produce asymmetric Ib/c supernovae or, if they sweep up more hydrogen, some fraction of the type IIb supernova population. These supernovae would be characterized by large asymmetries and, perhaps, larger 56Ni yields.
Alternatively, if the disk explosion model produces more symmetric explosions, the helium-merger model is more likely to produce a small subset of the type IIP supernovae and unless the 56Ni yield is different, it may be difficult to uncover differences between He-merger outbursts from typical core-collapse explosions. Again, it is likely that these bursts exhibit stronger asymmetries than normal supernovae and evidence of these asymmetries may be the only other characteristic differentiating these explosions from normal type IIP supernovae.
Supernovae have been observed that may exhibit a recent shell ejection caused by a helium shell ejection (SN2011ht: Roming et al. 2012). Using the same analysis as Section 3.1.1, we calculate the outer shell radii for both our low-mass helium cores and hydrogen stars; see Figure 11. Low-mass helium and hydrogen core mergers produce more shells with outer radii below 1–2 AU. The explosions from these mergers may, at peak, look very similar to comparable giant stars. A fraction (6% of hydrogen stars, 34% of low-mass helium cores) have outer shell radii beyond 10 AU that may produce the peculiar features of supernovae such as SN2011ht. The broad range of shell separations from these systems is in large part due to the fact that a sizable fraction of these systems (30% of hydrogen stars, 17% of low-mass helium stars) arise from systems in which the compact remnant is injected into its companion via natal kick.
Figure 11. Distribution of outer shell positions of our low-mass helium cores and hydrogen stars. The distribution is much broader than the high-mass helium cores, with many more systems with quite low outer shell radii. The broad range of shell separations from these systems is in large part due to the fact that a sizable fraction of these systems (30% of hydrogen stars, 17% of low-mass helium stars) arise from systems where the compact remnant is kicked into its companion.
Download figure:
Standard image High-resolution image4.3. Radio Bursts
If, in a GRB-like explosion, the jet sweeps up too much hydrogen to become relativistic, we will not observe a GRB. If the engine does not produce much 56Ni but the explosion remains asymmetric (preventing it from sweeping up much mass), the explosion will not produce strong optical emission either from nickel decay or shock heating (the two standard emission mechanisms for supernovae). Nonetheless, the jet will slow down in its surroundings, producing optically weak, radio loud outbursts that might be confused with radio loud outbursts from double neutron star mergers.
We still can not determine whether He-mergers explain a large population of low-luminosity GRBs, a small fraction of peculiar supernovae or other transients. Distinguishing between these possibilities requires more detailed observations of these different outbursts and a better understanding of the black hole accretion disk engine. These calculations provide a first set of diagnostics for comparison with upcoming surveys.
This project was funded in part under the auspices of the U.S. Dept. of Energy, and supported by its contract W-7405-ENG-36 to Los Alamos National Laboratory. K.B. acknowledges support from MSHE grant No. N203 404939.
- Abt H. A. 1983 ARA&A 21 343
- Barkov M. V. and Komissarov S. S. 2011 MNRAS 415 944
- Belczynski K., Bulik T. and Fryer C. L. 2013 ApJ 764 96
- Belczynski K., Bulik T., Heger A. and Fryer C. L. 2007 ApJ 664 986
- Belczynski K., Kalogera V. and Bulik T. 2002 ApJ 572 407
- Belczynski K., Kalogera V., Rasio F. A. et al. 2008 ApJS 174 223
- Blandford R. D. and Znajek R. L. 1977 MNRAS 179 433
- Bogomazov A. I., Lipunov V. M. and Tutukov A. V. 2007 ARep 51 308
- DiMatteo T., Perna R. and Naryan R. 2002 ApJ 579 706
- Dominik M., Belczynski K., Fryer C. L. et al. 2012 ApJ 759 1
- Duquennoy A. and Mayor M. 1991 A&AS 88 281
- Ellinger C. I., Young P. A., Fryer C. L. and Rockefeller G. 2012 ApJ 755 160
- Fryer C. L. 2009 ApJ 699 409
- Fryer C. L., Brown P. J., Bufano F. et al. 2009 ApJ 707 193
- Fryer C. L., Herwig F., Hungerford A. L. and Timmes F. X. 2006a ApJL 646 L131
- Fryer C. L., Hungerford A. L. and Young P. A. 2007a ApJL 662 L55
- Fryer C. L. and Kalogera V. 2001 ApJ 554 548
- Fryer C. L., Mazzali P. A., Prochaska J. et al. 2007b PASP 119 1211
- Fryer C. L., Rockefeller G. and Warren M. S. 2006b ApJ 643 292
- Fryer C. L. and Woosley S. E. 1998 ApJL 502 L9
- Fryer C. L., Woosley S. and Hartmann D. 1999 ApJ 526 152
- Hachinger S., Mazzali P. A., Taubenberger S. et al. 2012 MNRAS 422 70
- Heggie D. C. 1975 MNRAS 173 729
- Hobbs G., Lorimer D. R., Lyne A. G. and Kramer M. 2005 MNRAS 360 974
- Hurley J. R., Pols O. R. and Tout C. A. 2000 MNRAS 315 543
- Ivanova N., Justham S., Chen X. et al. 2012 arXiv:1209.4302
- Kawanaka N., Piran T. and Krolik J. H. 2012 arXiv:1211.5110
- Kobulnicky H. A. and Fryer C. L. 2007 ApJ 670 747
- Kobulnicky H. A., Smullen R. A., Kiminki D. C. et al. 2012 ApJ 756 50
- Komissarov S. S. and Barkov M. V. 2009 MNRAS 397 1153
- Kroupa P. and Weidner C. 2003 ApJ 598 1076
- Levine A. M., Rappaport S. A. and Zojcheski G. 2000 ApJ 541 194
- Liang E., Zhang B., Virgili F. and Dia Z. G. 2007 ApJ 662 111
- Mirabel I. F. 2007 CRPhy 8 7
- Passy J.-C., De Marco O., Fryer C. L. et al. 2012 ApJ 744 52
- Podsiadlowski P. and Ivanova N. 2003 From Twilight to Highlight: The Physics of Supernovae ed W. Hillebrandt and B. Leibundgut (Berlin: Springer) 19
- Podsiadlowski P., Ivanova N., Justham S. and Rappaport S. 2010 MNRAS 406 840
- Podsiadlowski P., Langer N., Poelerands A. J. T. et al. 2004 ApJ 612 1044
- Popham R., Woosley S. E. and Fryer C. L. 1999 ApJ 518 356
- Portegies-Zwart S. F., Dewi J. and Maccarone T. 2005 Ap&SS 300 247
- Roming P. W. A. et al. 2012 ApJ 751 92
- Surman R., McLaughlin G. C. and Hix W. R. 2006 ApJ 643 1057
- Surman R., McLaughlin G. C. and Sabbatino N. 2011 ApJ 743 155
- Thöne C. C., de Ugarte Postigo A., Fryer C. L. et al. 2011 Natur 480 72
- van den Heuvel E. P. J. and Yoon S.-C. 2007 Ap&SS 311 177
- Wellstein S. and Langer N. 1999 A&A 350 148
- Woosley S. E. and Heger A. 2006 ApJ 637 914
- Woosley S. E., Heger A. and Weaver T. A. 2002 RvMP 74 1015
- Xu X.-J. and Li X.-D. 2010 ApJ 716 114
- Yoon S.-C. and Langer N. 2005 A&A 443 643
- Zalamea I. and Beloborodov A. M. 2011 MNRAS 410 2302
- Zhang W. and Fryer C. L. 2001 ApJ 550 357