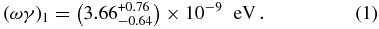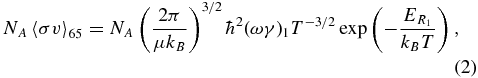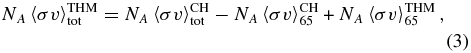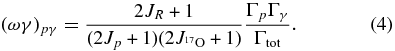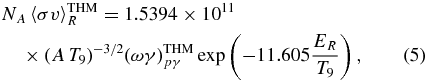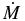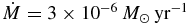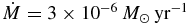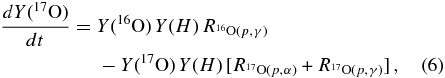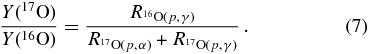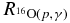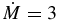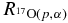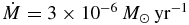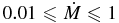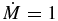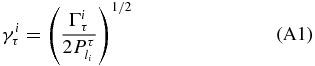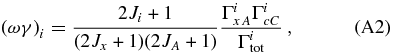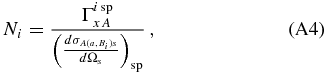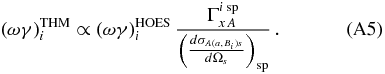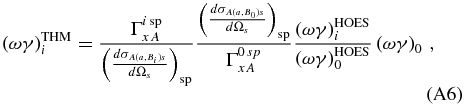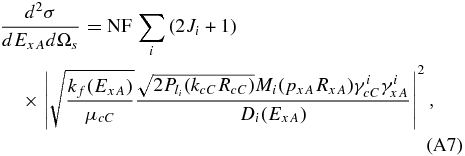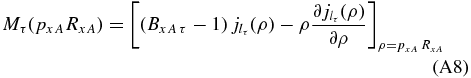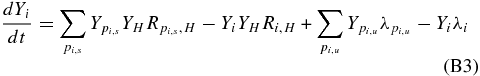ABSTRACT
In recent years, the Trojan Horse Method (THM) has been used to investigate the low-energy cross sections of proton-induced reactions on A = 17 and A = 18 oxygen isotopes, overcoming extrapolation procedures and enhancement effects due to electron screening. In particular, the strengths of the 20 keV and 65 keV resonances in the 18O(p, α)15N and 17O(p, α)14N reactions, respectively, have been extracted, as well as the contribution of the tail of the broad 656 keV resonance in the 18O(p, α)15N reaction inside the Gamow window. The strength of the 65 keV resonance in the 17O(p, α)14N reaction, measured by means of the THM, has been used to renormalize the corresponding resonance strength in the 17O + p radiative capture channel. As a result, more accurate reaction rates for the 18O(p, α)15N, 17O(p, α)14N, and 17O(p, γ)18F processes have been deduced, devoid of systematic errors due to extrapolation or the electron screening effect. Such rates have been introduced into state-of-the-art red giant branch and asymptotic giant branch (AGB) models for proton-capture nucleosynthesis coupled with extra-mixing episodes. The predicted abundances have been compared with isotopic compositions provided by geochemical analysis of presolar grains. As a result, an improved agreement is found between the models and the isotopic mix of oxide grains of AGB origins, whose composition is the signature of low-temperature proton-capture nucleosynthesis. The low 14N/15N found in SiC grains cannot be explained by the revised nuclear reaction rates and remains a serious problem that has not been satisfactorily addressed.
1. INTRODUCTION
Dust grains that form in the outer envelopes of low-mass stars or in ejecta from such stars provide one of the most important sources of information on the isotopic ratios of CNO isotopes in the atmosphere of red giant branch (RGB) and asymptotic giant branch (AGB) stars, as carbon, nitrogen, and oxygen isotopic ratios can be measured to a great accuracy and the production of radioactive nuclei such as 26Al and 41Ca can be measured in those stellar sources (Zinner 1998, 2005). According to the C/O regime in their envelopes, two different kinds of grains may be produced (Sharp & Wasserburg 1995). The condition C/O > 1 determines the formation of silicon carbide (SiC) grains; in the C/O < 1 regime, oxide grains originate, essentially Al2O3. Exhaustive classifications of SiC and oxide grains are reviewed in Zinner (2005) and Nittler (2009), respectively.
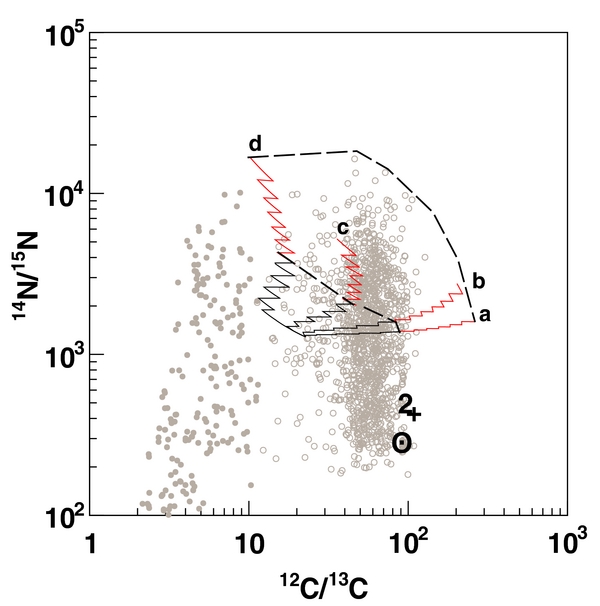
Following the standard classification, SiC grains can be divided into six populations, depending on the carbon and nitrogen isotopic ratios. Mainstream grains (∼93% of the total amount of SiC grains) have 10 ≲ 12C/13C ≲ 100, 200 ≲ 14N/15N ≲ 10, 000, and traces of 26Al, 22Ne, and s-elements (red ellipse in Figure 1). From consideration of the observed C and O isotopic ratios, it is commonly accepted that they condensed in the envelopes of Population I C-rich AGB stars. A + B grains, the second most abundant grains (4%–5%), roughly show the same spread in the nitrogen isotopic ratio but a smaller 12C/13C ratio, ranging in the 3–10 interval (blue ellipse in Figure 1). Different stellar sources have been indicated for these grains, the most likely candidates being AGB stars that underwent a more efficient extra-mixing, though other origins have been suggested (Amari et al. 2001). Nova, X, Y, and Z grains (dark gray, black, green, and light gray ellipses in Figure 1, respectively) are much less abundant and are believed to form in other astrophysical environments such as novae, supernovae, and low-metallicity AGB stars (Zinner et al. 2006).
Figure 1. SiC grain schematic overview (Amari et al. 2001; Zinner 2005) in the 14N/15N vs. 12C/13C isotopic ratio space. Mainstream and A+B grains (the most abundant ones) are indicated by a red and a blue ellipse, respectively. The less abundant X grains are marked by a black ellipse, Y grains are indicated by a green one, Z and nova grains are shown with a dark and a light gray ellipse, respectively.
Download figure:
Standard image High-resolution imageNittler et al. (1997) divided oxide grains into four groups on the basis of their location on the 17O/16O versus 18O/16O isotope space (Figure 2). Group 1 grains (17O/16O>3 × 10−4 and 10−3 < 18O/16O < 3 × 10−3) are considered to be born in the envelope of RGB stars (blue ellipse in Figure 2). Group 2 grains, which are characterized by an excess of 17O and a large 18O depletion with respect to the solar values (Asplund et al. 2009) and an 26Al/27Al ratio laying in the 0.001–0.02 range (red ellipse in Figure 2), are thought to form in oxygen-rich environments (Huss et al. 1992), such as AGB stars with masses <2 M☉ affected by extra-mixing phenomena, which deplete 18O in their envelopes and prevent them from reaching C/O ⩾ 1 (Wasserburg et al. 1995). Group 3 shows oxygen isotopic ratios smaller than the solar values and its origin is still uncertain (green ellipse in Figure 2), while group 4 grains (with 4 × 10−4 ⩽ 17O/16O ⩽ 2 × 10−3 and 2 × 10−3 ⩽ 18O/16O ⩽ 10−2) seem to have supernova progenitors (black ellipse in Figure 2).
Figure 2. Oxide grain subdivision according to Nittler et al. (1997) in the oxygen isotope space. Blue, red, green, and black ellipses are used for group 1–4 grains, respectively. The dashed lines demonstrate the solar 17O/16O and 18O/16O ratios, for the sake of comparison.
Download figure:
Standard image High-resolution imageAs circumstellar dust grains bear the fingerprints of nuclear burning and mixing processes occurring inside evolved stars, they can be effectively used to constrain stellar nucleosynthesis models (see, for instance, Herwig 2005, Nollett et al. 2003, and Palmerini et al. 2011b). Wasserburg et al. (1995) first identified the possibility that deep streams of material from the envelope across the radiative layers, flowing between the H-burning shell and the base of the stellar envelope. This provides a clear explanation of anomalous abundances of carbon and oxygen isotopes found in spectra of giant stars (Harris & Lambert 1984; Kahane et al. 1992; Wasserburg et al. 1995) and in presolar grains having them as progenitors. They also demonstrated the inadequacy of canonical stellar evolution and nucleosynthesis models to reproduce the chemical composition of giant stars (Boothroyd & Sackmann 1999). Since these models did not include such mass transport episodes among the other standard mixing phenomena (dredge-up), they were commonly identified as "extra-mixing."
Extra-mixing has proved successful in the interpretation of the 17O/16O versus 18O/16O isotopic ratios in oxide grains (Wasserburg et al. 1995). However, part of those grains, having 18O/16O < 0.0015 and 17O/16O < 0.005, were found to lay in a region not accessible by the mixing models (the so-called forbidden area marked with G in Figure 16 of Nollett et al. 2003). Recently, Palmerini et al. (2011b) demonstrated that the composition of those grains can also attributed to extra-mixing operating in very low mass AGB stars (M = 1 M☉). However, to reproduce the composition of the group 2 grains richest in 17O (WUSTL Presolar Database: http://presolar.wustl.edu/~pgd/), stars of masses as large as 1.7 M☉ were needed, which do not end as carbon-rich objects because of the occurrence of efficient extra-mixing phenomena.
Despite the fact that this scenario has been validated by several authors, a more difficult and unsolved issue regards the 14N/15N isotopic ratio found in grains of AGB origin, which could not be reproduced by standard models of stellar nucleosynthesis or with extra-mixing. We will here explore whether the revised reaction rates provide a solution to this problem.
In this work, we will focus on nitrogen and oxygen isotopic ratios in AGB and RGB stars in light of the recent 17O(p, α)14N and 18O(p, α)15N reaction cross section measurements at astrophysical energies, namely, for center-of-mass energies from about 0 to few hundreds keV (Sergi et al. 2010b, 2010a; La Cognata et al. 2008a, 2008b, 2009b, 2010a, 2010b). These investigations were triggered by the need of more accurate nuclear data, urged by the existing inconsistencies between the predicted and observed isotopic ratios in grains and by the poor knowledge of the 17O(p, α)14N and of the 18O(p, α)15N cross sections at such low energies (see, for instance, Angulo et al. 1999). The investigations discussed here have been performed by means of the Trojan Horse Method (THM; Spitaleri et al. 2011, and references therein), an indirect technique useful to study charged-particle-induced reactions at astrophysical energies that, with proper modifications, can be applied also to neutron-induced reactions (Tumino et al. 2005; Gulino et al. 2010; Lamia et al. 2008).
2. THE 17O/16O RATIO IN OXIDE GRAINS
Oxygen isotopes in group 1 and 2 oxide grains provide the most stringent constraints to stellar models with extra-mixing due to the fragility of 18O and the sensitivity of 17O abundance to temperature. For the generally adopted mixing rate, 18O is destroyed through the 18O(p, α)15N reaction while the maximum temperature experienced by the circulating material determines the 17O/16O isotopic ratio, which reflects the equilibrium value for CNO burning (Nollett et al. 2003; Palmerini et al. 2011b). The uncertainties on the predicted 17O/16O ratios are mostly attributable to the uncertainty affecting the cross section, in particular to the 65 keV resonance in the 17O(p, α)14N S-factor that dominates the reaction rate for 0.01 < T9 < 0.1 (José & Hernanz 2007).
The 65 keV resonance has been directly measured by Blackmon et al. (1995); the measurement turned out to be very difficult because of the Coulomb barrier suppressing the cross section and leading to Γp ∼ 22 neV, with an uncertainty of about 20%. Moreover, the screening induced in the nuclear Coulomb field by atomic electrons was not taken into account in the original work. At these energies, electron screening might determine an enhancement of the cross section larger than 15% for the 17O + p system, which cannot be neglected for astrophysical purposes (Assenbaum et al. 1987). Conversely, the THM indirect approach is not affected by electron shielding, thus a more accurate result could be achieved. The THM measurement (Sergi et al. 2010b, 2010a) yielded a reaction rate about 20% smaller than the one recommended by Chafa et al. (2007), still in agreement with it because of the experimental uncertainties. Such a discrepancy can derive from the electron screening effect, even though more precise direct and indirect investigations are mandatory for a definite interpretation.
From the discussion so far, it is apparent the pivotal role of the 17O(p, α)14N reaction during the AGB and the previous RGB phase. The first goal of the present work is the assessment of the effect of a slower 17O production due to the revised 17O(p, α)14N reaction rate.
3. THE 14N/15N RATIO IN SiC GRAINS
A long-standing issue concerns the 14N/15N isotopic ratio in SiC grains (Nollett et al. 2003; Palmerini et al. 2011b; Huss et al. 1997). In detail, about 50% of Mainstream and A+B grains show an 14N/15N isotopic ratio that is very small, approaching the solar value or values ∼10 times smaller. This is difficult to explain in any standard evolutionary model (Nollett et al. 2003). Indeed, according to any stellar nucleosynthesis model 15N is destroyed much faster than it is produced. Moreover, extra-mixing phenomena, though affording a reliable explanation for the low 12C/13C ratio found in these grains, lead to 15N destruction and 14N production, increasing the 14N/15N isotopic ratio. Therefore, different sites have been suggested where the lowest 14N/15N could be achieved, like explosive hydrogen burning (Huss et al. 1997). Other isotopic peculiarities characterizing Mainstream and A+B grains are not compatible with this burning scenario. Assuming the 14N/15N ratio in the Jovian atmosphere as the new estimate of the nitrogen isotopic ratio in the solar system (a factor of ∼1.5 larger than the terrestrial one; Fouchet et al. 2000, 2004; Owen et al. 2001) does not help to solve the puzzle (Palmerini et al. 2011b), even if this assumption is in agreement with the recent results of the Genesis mission, which found an 14N/15N in the protosolar nebula of around 440 (Marty et al. 2011). Instead, Nollett et al. (2003) showed that assuming a reduction of the initial 14N/15N ratio, which has to be far smaller than the solar value (∼70), the star would approach the RGB phase with a nitrogen isotopic ratio close to the solar one and the whole region of the Mainstream grains can essentially be filled by the occurrence of extra-mixing during the AGB phase. Such a low value for the nitrogen isotopic ratio in the local interstellar medium seems to be in contrast with the quoted measurements and with the recent finding of Adande & Ziurys (2012) and Gerin et al. (2009). However, the estimate of 14N/15N ratio in the Galaxy is still a widely debated topic because the differences in primary and secondary origins of the two nitrogen isotopes make very difficult to predict their trend in the galactic chemical evolution. Moreover, we have to underscore that the initial 14N/15N in the stars sampled by the dust grains cannot be ascertained and there is a great problem with nova models and yields (Nollett et al. 2003). It is possible that nuclear physics might shed light on 14N/15N isotopic ratio (Huss et al. 1997); in particular, the 15N(p, α)12C and 18O(p, α)15N reactions are the main 15N destruction and production channels, respectively, in H-burning of low-mass giants.
These facts motivated a new measurement of the 15N(p, α)12C reaction down to zero energy by means of the THM, since only extrapolations of direct data were present (Angulo et al. 1999 and references therein). No significant changes in the low-energy astrophysical factor were detected, which could justify a change in the 15N abundance in the outer layers of RGB or AGB stars (La Cognata et al. 2006, 2007, 2009a). Also in the case of the 18O(p, α)15N reaction, only extrapolation or spectroscopic studies were available below ∼70 keV where the presence of a resonance at about 20 keV and of a sub-threshold resonance at about −94 keV could dramatically alter the low-energy S(E)-factor (Angulo et al. 1999 and references therein). In contrast with the 15N(p, α)12C reaction, the THM measurement of the 18O(p, α)15N yielded a reaction rate ∼35% larger than the value in the literature at T9 ∼ 0.03, with an uncertainty about eight times smaller, thanks to an improved knowledge of the 20 keV resonance, while a negligible contribution of the sub-threshold state was confirmed (La Cognata et al. 2010a, 2010b, 2009b, 2008a, 2008b). As pointed out by Huss et al. (1997), converting a sufficient amount of 18O into 15N would result in a lower 14N/15N isotopic ratio, possibly leading to a better agreement with the values measured in the presolar grains.
Therefore, the second goal of the present work is the examination of the effect of the more precise 18O(p, α)15N reaction rate on the predicted 14N/15N values, according to the current models describing nucleosynthesis and mixing phenomena in low-mass giant stars.
4. THE TROJAN HORSE METHOD FOR RESONANCE REACTIONS
As discussed above, resonance reactions play a decisive role in many astrophysical contexts. Indeed, a resonance might dramatically enhance the astrophysical S(E)-factor so, when a resonance is present right at astrophysical energies, its measurement is crucial to pin down the astrophysical scenario. Unknown or unpredicted resonances might introduce large systematic errors in nucleosynthesis models. These considerations apply to low-energy resonances and to sub-threshold resonances as well, as they may produce sizable modifications of the S-factor due to, for instance, destructive interference with another resonance (see Rolfs & Rodney 1988 and Iliadis 2007 for a detailed discussion).
However, the presence of the Coulomb barrier, exponentially hampering the cross section at astrophysical energies, and of atomic electrons, shielding the nuclear charges (at least partially), makes the direct measurement of low-energy resonances not accurate enough or even impossible. Because of the Coulomb barrier, inside the Gamow energy window the cross section for reactions among charged particles drops below 10−12 barn, thus making statistical accuracy and signal-to-noise ratio very poor and the recourse to extrapolation from higher energy mandatory (Rolfs & Rodney 1988; Iliadis 2007).
Atomic electrons preclude the access to the bare-nucleus5 cross section, which is the nuclear physics input parameter for astrophysics (Assenbaum et al. 1987; Fiorentini et al. 1995; Strieder et al. 2001). In fact, electron screening acts differently in stellar plasma and in the laboratory, where projectile and target nuclei are in the form of ions and atoms or molecules, respectively. Atomic electrons screen the nuclear charges, thus determining an enhancement of the cross section at the lowest energies, which is not related to nuclear physics. The bare-nucleus cross section is again deduced through extrapolation of the cross section from higher energies, where the effect of the electron cloud is negligible. As a result, large uncertainties can be introduced into the astrophysical models because of an incorrect estimate of the relevant cross sections. The uncertainty introduced by the electron screening is even larger in the case of resonance reactions, since no extensive investigations are available, in contrast with the non-resonant case (Sergi et al. 2010b; Strieder et al. 2012).
The THM (Baur 1986; Spitaleri 1990; Spitaleri et al. 1999, 2011; Lamia et al. 2007; Pizzone et al. 2005a, 2011; Tumino et al. 2006) allows one to access the low-energy bare-nucleus cross section of an A(x, c)C reaction by extracting the quasi-free (QF) contribution to a suitable A(a, cC)s reaction, having three particles in the exit channel. Particle a, characterized by a prominent x⊕s cluster structure, is referred to as Trojan horse nucleus as it is used to transfer the participant cluster x. Indeed, if the beam energy is chosen larger than the Coulomb barrier for the A+a interacting system, the breakup of the Trojan horse nucleus takes place inside A nuclear field. The transferred particle x is used to feed the excited states of B, later decaying into c+C. In QF kinematics, the other constituent cluster s is emitted without interacting with the system B, thus behaving as a spectator to the A(x, c)C sub-process.
Because the A(a, cC)s reaction is performed at high energies (several tens of MeV), the cross section of the A(x, c)C process is not hindered by the Coulomb interaction of the target–projectile system, while no electron screening enhancement is spoiling the nuclear information. Anyway, particle x is virtual so the A(x, c)C THM cross section is half-off-energy-shell (HOES) and cannot be right juxtaposed to the direct (on-energy-shell, OES) cross section6 (La Cognata et al. 2007). The method has been widely applied to study non-resonant reactions, leading to the extraction of the corresponding S(E)-factor at Gamow energies, devoid of electron screening effects (Spitaleri et al. 2004, 2011; Lamia et al. 2012; La Cognata et al. 2005; Tumino et al. 2011; Pizzone et al. 2003, 2005b; Wen et al. 2008). In the case of resonance reactions, the so-called modified R-matrix approach (Mukhamedzhanov et al. 2008; La Cognata et al. 2009a, 2010a, 2010b; Mukhamedzhanov 2011) has been introduced to extract the physical information of interest from the QF reaction yield.
A detailed discussion about TH formalism for resonance reactions can be found in Appendix A. Here we will focus on the impact of the measured TH reaction rate on astrophysical sites.
5. THE 18O(p, α)15N REACTION RATE
At temperatures of few 107 K, typical of the H-shell of low-mass AGB stars, the energy interval where the 18O(p, α)15N is most effective ranges from about 20 to 70 keV. Though nine resonances show up in the 18O(p, α)15N cross section inside the 0–1 MeV energy interval, only the 20, 144, and the broad 656 keV resonances are relevant to astrophysics as they determine the reaction rate (Angulo et al. 1999). These resonances have been subject of several direct experimental investigations (Mak et al. 1978; Lorenz-Wirzba et al. 1979; Christensen et al. 1990) as well as of many spectroscopic studies (Yagi 1962; Champagne & Pitt 1986; Wiescher & Kettner 1982; Schmidt & Duhm 1970), nevertheless the reaction rate for this process has considerable uncertainty (Angulo et al. 1999). Indeed, only the contribution of the 144 keV resonance has been soundly established by Lorenz-Wirzba et al. (1979).
With regard to the 20 keV resonance, its strength is known only from spectroscopic measurements performed through the transfer reaction 18O(3He, d)19F (Champagne & Pitt 1986) and the direct capture reaction 18O(p, γ)19F (Wiescher et al. 1980). Indeed, because of the Coulomb suppression, the expected strength is exceedingly small, about 2 × 10−18 eV (Wiescher & Kettner 1982), making its measurement very challenging. The values of the resonance strengths ωγ in the literature might be potentially affected by large and not-well-defined uncertainties because they are strongly dependent on the optical model potentials adopted in the data analysis. Since in the THM approach no Coulomb hindrance affects strengths, it is well suited to extract the ωγ parameter of the 20 keV resonance. In particular, since such resonance is very narrow, according to the measurements in the literature, the narrow-resonance formalism of THM has been employed to obtain its resonance strength. A detailed discussion is given in La Cognata et al. (2008a, 2009b, 2010b); here we only report on the results. By normalizing to the well-known resonance at 144 keV (Equation (A6)), our TH measurement results in ωγ = 8.3+3.8−2.6 × 10−19 eV, which is in good agreement with NACRE (Angulo et al. 1999), ωγ = 6+17−5 × 10−19 eV, but 10 times more accurate. Indeed, NACRE-recommended value is based on various kinds of estimates while the THM result is obtained from experimental data, thus the accuracy of the resonance strength has been greatly enhanced. As a cross check, the strength of the 90 keV resonance was extracted as well, leading to ωγ = (1.76 ± 0.33) × 10−7 eV, in good agreement with the strength given by NACRE, (1.6 ± 0.5) × 10−7 eV.
The resonance at 656 keV gives strong contributions both at low and high temperatures, as it is comparatively broad, Γtot varying from 100 to 300 keV according to the different measurements (Yagi 1962; Lorenz-Wirzba et al. 1979; Mak et al. 1978). Such discrepancy is due to the poor knowledge of the α partial width and, as a consequence, no accurate reaction rate could be determined. Angulo et al. (1999), for instance, evaluated the contribution of such resonance to the total reaction rate by averaging the rates resulting from the numerical integration of the cross sections given in Yagi (1962) and Lorenz-Wirzba et al. (1979). As it is discussed in La Cognata et al. (2010a), the origin of such discrepancy is apparent when considering the absolute value of the experimental S(E) factors around Ecm = 660 keV. Systematic errors make the deduced reaction rates potentially flawed and have motivated an indirect study via the THM. As reported in La Cognata et al. (2010a), a simultaneous fit of the direct (Lorenz-Wirzba et al. 1979) and THM S(E)-factor in the 0.5–0.9 MeV energy range has been performed taking into account interference effects to provide a conclusive set of resonance parameters. A total width Γtot = 199 ± 3 keV was obtained, significantly improving the accuracy of the resonance parameter of the 8.65 MeV 19F state, the error on its width changing from ∼50% to 1.5%, while the resonance energy turns out to be about 50 keV smaller than quoted in the literature. As a result, a factor of two increase is found in the reaction rate due to the recommended resonance parameters.
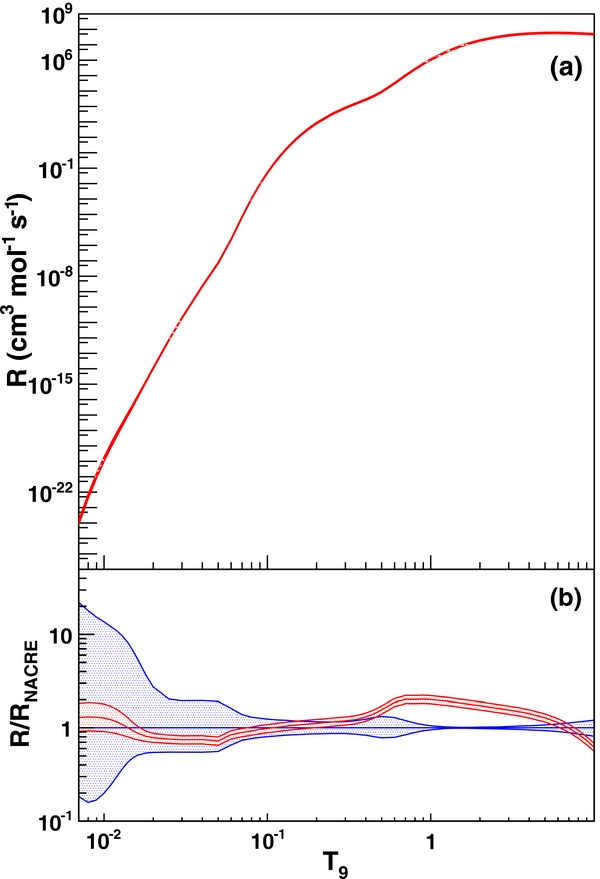
Figure 3(a) shows the reaction rate evaluated by means of the THM data, as a function of the temperature T9, that is, expressed in units of 109 K. To compare it with the one usually adopted in astrophysical calculation, the ratio of the THM rate to the one in NACRE (Angulo et al. 1999) is shown in Figure 3(b) as a red band, the width of the band underscoring the uncertainty affecting the calculated reaction rate. The blue band shows the range on uncertainty characterizing the Angulo et al. (1999) rate. Clearly, the THM reaction rate shows a much narrower band than the NACRE one over the whole temperature range, especially at small values of T9, thanks to the enhanced precision of the strength of the 20 keV resonance as measured be means of the THM.
Figure 3. 18O(p, α)15N reaction rate calculated using the THM nuclear physics input. In panel (a) the reaction rate is shown, in panel (b), for ease of comparison, its ratio to the NACRE one (Angulo et al. 1999) is shown. In particular, the red band marks the reaction-rate interval allowed by experimental uncertainties on the THM data. The blue band is used to display the range on uncertainty characterizing the direct data in the NACRE compilation.
Download figure:
Standard image High-resolution image6. THE 17O(p, α)14N REACTION RATE
The relevant stellar temperatures for the 17O nucleosynthesis are in the ranges T9 = 0.01–0.1 for RGB and AGB stars, and T9 ∼ 0.4 for classical nova explosions (José & Hernanz 2007). Thus, the 17O(p, α)14N reaction cross section has to be precisely known in the center-of-mass energy range Ec.m. = 0.017–0.370 MeV. In this range the 17O(p, α)14N reaction cross section is dominated by two resonances: one at about 65 keV above the 18F proton threshold, corresponding to the Ex = 5.673 MeV 18F level, and the other at 183 keV (Ex = 5.786 MeV).
During the last decades the 17O(p, α)14N reaction cross section has been the subject of several experimental investigations (Brown 1962; Rolfs & Rodney 1975; Kieser et al. 1979; Landre et al. 1989; Blackmon et al. 1995; Fox et al. 2004, 2005; Chafa et al. 2007; Moazen et al. 2007; Newton et al. 2007). In particular, in the last years, several measurements (Chafa et al. 2007; Fox et al. 2004; Moazen et al. 2007) of the Ec.m.R = 183 keV resonance have drastically reduced the uncertainties on both 17O(p, α)14N and 17O(p, γ)18F reaction rates at temperatures relevant for explosive H-burning. By contrast, only the direct measurement of the 65 keV resonance performed by Blackmon et al. (1995) is available for the (p, α) channel. In this work, a proton width Γp = 22 ± 3stat ± 2target+2−1 beam neV was inferred, which is the smallest measured proton-capture width. However, the electron screening effect was not taken into account by Blackmon et al. (1995). Indeed, at these energies, atomic electron clouds can shield the nuclear charges of the interacting nuclei and might determine an enhancement of the cross section larger than 15% (Assenbaum et al. 1987) for the 17O + p system that cannot be neglected for astrophysical purposes.
In Sergi et al. (2010b), the strength of the 65 keV resonance (ωγ)1 was obtained by applying the THM to the QF 2H(17O,14Nα)n reaction. By normalizing to the weighted average of the three values for the 183 keV resonance strength in the literature (Chafa et al. 2007; Moazen et al. 2007; Newton et al. 2007), (ωγ)2 = (1.66 ± 0.10) × 10−3 eV, the following result was obtained for the 65 keV resonance strength (Sergi et al. 2010b):
This result was used to calculate its contribution to the total reaction rate adopting the narrow resonance approximation, whose conditions are satisfied for the resonance under investigation (Rolfs & Rodney 1988; Iliadis 2007). According to this approximation, the contribution of the 65 keV resonance to the rate R is given by
where μ is the reduced mass for the projectile–target system, kB is the Boltzmann constant, and T is the temperature of the astrophysical site.
To perform the calculation of the 17O(p, α)14N reaction rate including the obtained strengths of the 65 keV resonance (ωγ)1, first the 65 keV resonant reaction rate NA〈σv〉CH65 obtained by Chafa et al. (2007) was reproduced by using the parameters reported in Table 1, and then the individual reaction rate NA〈σv〉THM65 for the 65 keV resonance was calculated introducing the (ωγ)1 value from Sergi et al. (2010b) into Equation (2). Thus, the total reaction rate NA〈σv〉THMtot can be calculated using the following relation:
where NA〈σv〉CHtot is the total reaction rate established in Chafa et al. (2007). The reaction-rate calculation performed by Chafa et al. (2007) includes the 5.6034, 5.6716, and 5.7898 MeV levels of 18F and 15 additional levels at higher energies as in Angulo et al. (1999). In particular, in the Chafa et al. (2007) work the interference effect between the two resonances at ER = 183 keV and at ER = 1202.5 keV was investigated and the proton width of the sub-threshold level at 5.6034 MeV revaluated by calculating its single-particle reduced width using a Woods–Saxon potential with the same parameters adopted in Landre et al. (1989) to extract the spectroscopic factor (A. M. Mukhamedzhanov 2011, private communication). Regarding the other levels that are not present in Table 1, the adopted parameters are the same as in NACRE (Angulo et al. 1999).
Table 1. Summary of the Parameters of the Six Most Important States in 18F for the 17O(p, α)14N Reaction-rate Calculation at Temperatures T9 < 0.3 Adopted in Chafa et al. (2007)
| ER | EX | Jπ | Γp | Γα | Γγ |
|---|---|---|---|---|---|
| (keV) | (keV) | (eV) | (eV) | (eV) | |
| −3.12 ± 0.57 | 5603.38 ± 0.27 | 1+ | ⋅⋅⋅ | 42.8 ± 1.6 | 0.485 ± 0.046 |
| 65 ± 0.5 | 5671.6 ± 0.2 | 1− | (19 ± 3)×10−9 | 130 ± 5 | 0.45 ± 0.02 |
| 183.3 ± 0.6 | 5789.8 ± 0.3 | 2− | (3.8 ± 0.5)×10−3 | 6.8 ± 3.0 | (9.4 ± 3.6)×10−3 |
| 556.7 ± 1.0 | 6163.2 ± 0.9 | 3+ | (14.0 ± 0.5)×103 | 3.86 ± 0.72 | (37.7 ± 8.6)×10−2 |
| 676.7 ± 1.0 | 6283.2 ± 0.9 | 2+ | (10.0 ± 0.5)×103 | 13.9 ± 0.55 | 0.64 ± 0.14 |
| 1202.5 ± 5.0 | 6809 ± 5 | 2− | 14.5×103 | 64.5×103 | ⋅⋅⋅ |
Download table as: ASCIITypeset image
Figure 4(a) shows the reaction rate evaluated by means of the THM data, as a function of temperature T9. For better comparison, Figure 4(b) shows the ratio (red middle line) between the reaction rate R extracted here, including the 65 keV resonance strength measured by means of the THM, and the reaction rate RChafa of Chafa et al. (2007). The other red lines mark the position of the upper and lower limits as deduced in Sergi et al. (2010b). The blue band represents the Chafa et al. (2007) reaction-rate range allowed for by the experimental uncertainties. A small difference (∼20%) can be seen in the range T9 = 0.02–0.1, while no significant differences are present for T9 > 0.2 where the contribution of the 65 keV resonance to the reaction rate is negligible.
Figure 4. 17O(p, α)14N reaction rate calculated using the 65 keV resonance strength obtained through the THM. In panel (a) the reaction rate is shown, in panel (b) its ratio to the Chafa et al. (2007) rate is shown. In particular, the red band marks the reaction-rate interval allowed by experimental uncertainties on the 65 keV resonance strength only. The blue band, instead, is used to display the range on uncertainty characterizing direct data (Chafa et al. 2007).
Download figure:
Standard image High-resolution image7. THE 17O(p, γ)18F REACTION RATE
The definition of the resonance strength (Rolfs & Rodney 1988; Iliadis 2007) entails that the ωγ parameter of the ER = 65 keV resonance in the 17O(p, α)14N reaction is proportional to the proton partial width Γp, the exit channel partial width essentially coinciding with the total width, through the statistical factor. Therefore, the 65 keV resonance strength measured by means of the THM (Sergi et al. 2010b, 2010a) requires a rescaling of the partial width Γp and, as a consequence, of the strength of the 65 keV resonance in the 17O(p, γ)18F channel, being proportional to Γp as well:
The THM-scaled resonance strength of the lowest energy resonance is then (ωγ)THMpγ = (1.27+0.26−0.22) × 10−11 eV, to be compared with (1.64 ± 0.28) × 10−11 eV as given in the literature and in the most recent reviews (Chafa et al. 2007; Adelberger et al. 2011; Iliadis et al. 2010). This ∼30% difference between the THM-scaled resonance strength and the value in the literature might determine significant consequences on astrophysics motivating an evaluation of its reaction rate.
Chafa et al. (2007) have reported that the direct capture process strongly affects the total reaction rates for T9 < 0.8. Therefore, thanks to the THM measurement of the (ωγ)pα resonance strength, only the contribution to the reaction rate due to resonance radiative capture can be presently updated. Moreover, the contributions to the reaction rate of resonance tails were found to be small for T9 > 0.03. But at lower temperatures, and in particular inside the 0.006 < T9 < 0.06 range of interest for AGB nucleosynthesis, the tail contribution from the 18F level at Ex = 5.6716 MeV is dominant. Again, the resonance THM approach is sensitive to the area subtended by the resonance peak and not to its shape, allowing for the extraction of the strength parameter but not of the S-factor at the Gamow energy, needed to evaluate the tail contribution (Rolfs & Rodney 1988; Iliadis 2007).
For these reasons, the modified 17O(p, γ)18F reaction rate including the THM-scaled strength of the 65 keV resonance has been obtained by inserting its contribution:
in the place of the corresponding one given by Chafa et al. (2007), into their recommended reaction rate. The THM-modified reaction rate is displayed in Figure 5(a) as a red line. For comparison, its ratio to the Chafa et al. (2007) rate is displayed as a red band in Figure 5(b), the recommended, upper and lower limits marked by red lines. The upper and lower limits account for the uncertainty on the THM-scaled resonance strength. In the same way, a blue band is used to show the Chafa et al. (2007) reaction rate. Figure 5(b) clearly demonstrates that a 20% reduction of the reaction rate between T9 ∼ 0.03 and ∼0.09 is present due to the reduction of the proton partial width Γp as a consequence of the THM measurement of the 65 keV resonance strength. As discussed in Sergi et al. (2010b, 2010a), it can be attributed to the enhancement of the Coulomb barrier penetration due to the electron screening of nuclear charges, though further studies are necessary to achieve sounder conclusions.
Figure 5. 17O(p, γ)18F reaction rate calculated using the THM-scaled strength of the 65 keV resonance. In panel (a) the reaction rate is shown, in panel (b), for ease of comparison, the ratio of results by the THM to that of Chafa et al. (2007) is shown. In particular, the red band marks the reaction-rate interval allowed by experimental uncertainties on the THM strength. The blue band is used to display the range of uncertainty characterizing the direct data.
Download figure:
Standard image High-resolution image8. EFFECT OF THE NEW REACTION RATES ON RGB AND AGB NUCLEOSYNTHESIS
In this section, the astrophysical consequences of the revised rates are reviewed. To this purpose, repercussions on models not including extra-mixing are first analyzed, regarding both abundances and stellar evolution. In the canonical models (not including extra-mixing phenomena), the chemical compositions of low-mass-giant (M ⩽ 2.5–3 M☉) envelopes are determined by convective mixing episodes, namely, the first dredge-up (FDU) at the beginning of the RGB phase and the third dredge-up (TDU), which follow each He-burning thermal instability during the AGB phase. Two facts have to be preliminarily underscored to understand the calculation outcome. The 14N(p, γ)15O reaction, which is the slowest step of the CNO cycle, sets the timescale of shell H-burning that is the main stellar energy source during the RGB and AGB phase. Moreover, since 14N and 16O are the most abundant isotopes of their elements (by a factor of 200) in this region, the rates by which they undergo proton captures also fix the oxygen and nitrogen isotopic mix resulting from the FDU. Consequently, negligible effects arise if the THM reaction rates for 17O(p, α)14N, 18O(p, α)15O, and 17O(p, γ)18F are introduced in the calculations. In the same way, the choice of these reaction rates does not affect the evolution of giant stars nor the evolution of the O/H ratio in the stellar surface.
Following our earlier work (Palmerini et al. 2011b), here we use the revised solar abundances by Asplund et al. (2009), and the 14N(p, γ)15O and 16O(p, γ)17F reaction rates from Adelberger et al. (2011). We run our calculations as a post-process of the last version of the FRANEC evolutionary model in which the new low-temperature opacities are used (Cristallo et al. 2009). Moreover, the new estimate of the nitrogen isotopic ratio in the Jovian atmosphere (Fouchet et al. 2000; Owen et al. 2001) is assumed as the initial one for our models. Such upgrades slightly affect the stellar structure, increasing of about 10% the temperature of the H-burning shell and deepening the penetration of the envelope during the FDU (Palmerini et al. 2011b). By contrast, the 14N/15N isotopic ratio in the stellar envelopes after the FDU is reduced and the 17O/16O is increased because of the these changes. In particular, the nitrogen isotopic ratio is mainly affected by the assumption of a somewhat lower initial value, while the oxygen isotopic composition is affected by both the new abundances and the new rate for proton captures on 14N; for a 2 M☉ and solar-metallicity star, the 17O/16O is larger by a factor of two than in the previous works by Wasserburg et al. (1995), Boothroyd & Sackmann (1999), and Nollett et al. (2003). It is worth noting that the CNO isotopic composition after the FDU of 1.5 and 2 M☉ RGB stars reported by these authors are not far from the ones obtained in more recent studies where the effects of the stellar rotation on surface abundances are considered (e.g., Charbonne & Lagarde 2010)
The modifications in the reaction rates presented here using the THM are found to be important in calculating the O isotopic compositions in AGB and RGB stars. From consideration of the results on oxide grains in stellar ejecta, it remains necessary to have extra-mixing processes to reproduce the 18O/16O, 26Al/27Al, and 12C/13C isotopic ratios observed in grains and stellar spectra. Since extra-mixing takes place at relatively low temperatures (T ⩽ 2–3 × 107 K), the new 17O(p, α)14N, 18O(p, α)15O, and 17O(p, γ)18F reaction rates can affect the star surface composition while the (p, γ) reaction on 14N and 16O are not active, their cross sections being much smaller than those of (p, α) reactions.
From the considerations above, we conclude that no major change is caused by the new reaction rates in normal stellar evolution models without extra-mixing, throughout the AGB stage (when the H-burning temperatures are higher than during the previous RGB phase). We now consider the effect of these revised rates when they are used in the extra-mixing calculations to analyze their impact on p-capture nucleosynthesis coupled with extra-mixing of low-mass RGB and AGB stars. First, we compare our results with those obtained from standard nuclear physics inputs, namely, the reaction rates recommended in Adelberger et al. (2011), Chafa et al. (2007), and Angulo et al. (1999). Second, the computed isotopic ratios are compared with the results from the analysis of oxide and SiC grains of AGB and RGB origin.
8.1. Consequences of the Revised Reaction Rates on the Prediction for Presolar Grain Composition Including Extra-mixing
For the sake of comparison, here we adopt the same code for extra-mixing calculation (see Appendix B for details), the same stellar evolutionary models and solar metallicity as in Palmerini et al. (2011b), limiting the differences to the reaction rates for proton captures on 17O and 18O. The isotopic abundances in the stellar envelopes after the FDU, which are assumed as the initial chemical composition for extra-mixing calculations, are taken from the FRUITY database (http://fruity.oa-teramo.inaf.it), with the exception of oxygen and nitrogen isotope abundances that are from Table 2 of Palmerini et al. (2011b).
8.1.1. Oxide Grains
The C/O < 1 regime, where presolar oxide grains may form, is typical of the envelope of an RGB star. It is attained also during the AGB stage by objects more massive than ∼4.5 M☉ (Boothroyd et al. 1995), where the temperature at the base of the convective envelope is high enough to trigger hot bottom burning (HBB), and by low-mass stars (M ⩽ 1.7 M☉) that undergo a low number of TDU episodes. For these stars, the moderated C-enrichment is compensated for by 12C depletion due to extra-mixing (Nollett et al. 2003; Busso et al. 2010; Palmerini et al. 2011b). It was pointed out by Lugaro et al. (2007) and Iliadis et al. (2008) that massive AGB star nucleosynthesis cannot lead to a possible explanation for the isotopic mix of group 2 grains. Instead, reliable candidate progenitors for these grains are AGB stars with masses ⩽1.7 M☉ affected by extra-mixing phenomena. Stellar models of solar composition are assumed as progenitors of group 1 and 2 oxide grains, M ⩽ 2 M☉ and 1–1.2 M☉, respectively. In this section, we will assess the effects of the new 17O + p reaction rates on low-mass red-giant nucleosynthesis, contrasting our model results with the composition of oxide grains belonging to groups 1 and 2.
In order to understand the effect of the revised reaction rates on the oxygen isotopic ratios in oxide grains, we first compare the results discussed by Nollett et al. (2003) with those obtained by Palmerini et al. (2011b) to pin down the differences in the stellar model. Then, the conclusions of the work by Palmerini et al. (2011b) will be compared with the outcome of the calculations employing the new 17O + p reaction rates.
In Figure 6, the distribution of group 1 (open circles) and 2 (filled circles) oxide grains on the 17O/16O versus 18O/16O plane is displayed. The regions that can be covered by extra-mixing calculations varying the model parameters (Δ, the mixing depth, between 0.1 and 0.22 and , the mixing rate, between 0.03 × 10−6 and 3 × 10−6 M☉ yr-1) are delimited by solid lines. Calculations were performed on stars of solar metallicity, with 1 M☉ ⩽ M ⩽ 1.5 M☉. In more details, the areas demarcated by black and blue solid lines highlight the envelope composition obtained by Nollett et al. (2003) and Palmerini et al. (2011b), respectively. In the same figure, the region of oxygen isotopic ratios that can be populated adopting the Palmerini et al. (2011b) model but using the reaction rates presented in this paper is bound by red lines. Both Nollett et al. (2003) and Palmerini et al. (2011b) assumed the isotopic abundances resulting after the FDU as the initial values for the subsequent extra-mixing calculations. These starting values, for different stellar masses, are indicated by the almost vertical dashed line on the right part of Figure 6, stopping at B (Nollett et al. 2003) or at C (Palmerini et al. 2011b) for a 2 M☉ star. In addition, the FDU composition for models with 1.5 M☉ is marked with D (Nollett et al. 2003) or E (Palmerini et al. 2011b). Figure 6 shows that the 17O/16O range, spanning the 3.7 × 10−4 and 5 × 10−3 interval, is accounted for by the oxygen isotopic mix left by FDU in the envelopes of RGB stars of 1–2 M☉ and solar metallicity, as reported by Palmerini et al. (2011b). They computed the FDU using the new version of the FRANEC code (Cristallo et al. 2009, 2011), including the 14N(p, γ)15O reaction rate from LUNA Collaboration et al. (2006) and Adelberger et al. (2011). By contrast, the 2 M☉ RGB star model by Nollett et al. (2003) reached instead a smaller 17O/16O ratio, which is indicated by the label B. Owing to the larger initial 17O/16O ratio, most of group 1 grains (open circles) gather along stellar model predictions for the RGB phase (maybe including a shallow mixing) and the explanation of grains with 17O/16O ⩾ 0.001 does not require the occurrence of more massive objects of 6–7 M☉, affected by HBB (Wasserburg et al. 1995; Nollett et al. 2003). The introduction of extra-mixing phenomena during the AGB stage allows calculations to reproduce the composition of group 2 oxide grains (solid circles in Figure 6). Anyway, only the red and blue lines encompasses most of the group 2 grains, the ones richest in 17O being missed by Nollett et al. (2003). This has to be attributed to the different reaction rates employed by Nollett et al. (2003), from the NACRE compilation (Angulo et al. 1999), while the red and blue regions have been determined using updated 14N(p, γ)15O and 17O + p reactions rates. Finally, it is worth noting that most of grains belonging to the "forbidden" area G in Figure 6 (using the definition given by Nollett et al. 2003) are now accounted for by extra-mixing models. They are embraced by the blue and red loci, supposing that extra-mixing has occurred in a ∼1 M☉ AGB star that has undergone extra-mixing also during the previous longer RGB stage and introducing into calculations the p-capture rates on oxygen isotopes reported by Chafa et al. (2007) and Adelberger et al. (2011) or in the present work.
Figure 6. Oxygen isotopic mix for a sample of oxide grains. Open and solid circles mark the 17O/16O vs. 18O/16O ratios for group 1 and 2 oxide grains, respectively (data are taken from WUSTL Presolar Database: http://presolar.wustl.edu/~pgd/). The AC dashed curve displays the oxygen isotopic mix left by the FDU in envelopes of solar-metallicity RGB stars with masses from 1 (filled square labeled by A) to 2 M☉ (filled square labeled by C) as resulting from the recent calculation by Palmerini et al. (2011b). The AB dashed curve instead represents the chemical composition after the FDU for the same range of masses but computed using the previous version of the FRANEC code (Straniero et al. 1997) and assumed by Nollett et al. (2003). The black solid curve delimits the area of oxygen isotopic ratios that can be accounted for by extra-mixing at play in AGB stars with masses from 1 to 1.5 M☉ (marked by D) presented by Nollett et al. (2003, see their Figure 16, in particular). Also, the range of values covered by HBB (H area) and the region not accessible by extra-mixing (G area) are displayed. The blue curve delimits the area of oxygen isotopic ratios that can be accounted for by extra-mixing at play during the RGB and AGB phase on stars with masses from 1 to 1.5 M☉ (marked by E), as computed by Palmerini et al. (2011b, which considered cross sections from Chafa et al. 2007 and Adelberger et al. 2011), while the red curve shows the results obtained by repeating the same calculation but by using the TH 17O(p, α)14N and 17O(p, γ)18F reaction rates, discussed in this paper.
Download figure:
Standard image High-resolution imageTo assess the effect of the new 17O + p reaction rates on low-mass red-giant nucleosynthesis, in Figure 7 we present a comparison between extra-mixing computations performed using the 17O(p, α)14N and 17O(p, γ)18F reaction rates discussed in this paper and the ones in Chafa et al. (2007). The almost vertical dashed line on the right (the same as the line AC in Figure 6) indicates the oxygen isotopic mix left in the envelopes of RGB stars with masses from 1 to 2 M☉ by the FDU (black squares are used to mark the results for several stellar masses). As already discussed, extra-mixing phenomena during the RGB and AGB stages are needed to reproduce the composition of group 2 oxide grains lying in the 18O-poor region of Figure 7. Red and black curves represent the results of extra-mixing nucleosynthesis models, different curves referring to distinct extra-mixing sets of parameters, different colors to alternative reaction rates, black for the Chafa et al. (2007) and red for the THM ones. In the case of a 1.2 M☉ AGB star (solid lines), the mixing depth Δ was set to 0.1 and 0.22 while the mixing rate was taken equal to 1 × 10−6 and 3 × 10−6 M☉ yr-1, getting the lines labeled with letters a–d (see Figure 7 caption for details). In the case of a 1 M☉ AGB star (dotted lines), we assumed Δ = 0.22 and during the RGB phase and Δ = 0.1 and during the AGB stage.
Figure 7. Comparison between the oxygen isotopic mix measured in a sample of oxide grains (the same as the ones reported in Figure 6) and extra-mixing calculations performed using the model in the work by Palmerini et al. (2011a) for a 1 M☉ and a 1.2 M☉ solar-metallicity star. The initial values assumed for our calculations correspond to the composition resulting from the FDU, as determined by Palmerini et al. (2011a). For solar-metallicity RGB stars with masses from 1 to 2 M☉, the initial oxygen isotopic mix is given by the almost vertical black dashed line on the right (This curves is the AC one reported in Figure 6). The solid curves show the evolution of the O-isotopic ratios in the envelope of the 1.2 M☉ star calculated for the four most efficient cases, namely, (a) Δ = 0.1, ; (b) Δ = 0.1, ; (c) Δ = 0.22, ; and (d) Δ = 0.22, . The effects of extra-mixing in the composition of the 1 M☉ are shown instead just for Δ = 0.22 and during the RGB phase and Δ = 0.1 and during the AGB stage (dotted lines). The extra-mixing calculations executed using the THM 17O(p, α)14N and 17O(p, γ)18F reaction rates are drawn in red, while the results obtained by using the rates by Chafa et al. (2007) are reported in black.
Download figure:
Standard image High-resolution imageFigure 7 clearly shows that models attain better agreement with the 18O/16O versus 17O/16O values in group 2 grains when introducing into calculations the THM revised reaction rates, for the same extra-mixing conditions. In more details, the lowest 18O/16O values exhibited by group 2 grains can be explained by the most efficient extra-mixing case (Δ = 0.1 and ) applied to a 1.2 M☉ AGB model (curve b). Under this condition, the resulting isotopic mix in the stellar envelope will closely resemble the one of CNO equilibrium at a temperature TP and the 17O/16O "end point" reached by extra-mixing model only depends on the mixing depth. The temporal evolution of 17O abundance during the CNO cycle is determined by the equation
where Y(i) means the abundance in number of the ith isotope and any reaction rate R is temperature and density dependent. From the previous equation, the equilibrium value of the 17O/16O ratio turns out to be
Figure 8 displays the 17O/16O equilibrium abundances deduced from Equation (7) as a function of the temperature T9. This plot has been already proposed by Nollett et al. (2003, compare their Figure 8), where the reaction rates reported in the NACRE compilation (Angulo et al. 1999) had been used to establish the 17O/16O equilibrium values. In Figure 8, the 16O(p, γ)17F reaction rate has been kept fixed at the recommended value of Adelberger et al. (2011). Two rates of the 17O(p, α)14N and 17O(p, γ)18F reactions were instead considered, a black solid line being used when the rates given in Chafa et al. (2007) were introduced into the calculations, a red solid line for the THM rates given in the previous sections. In both cases, short-dashed lines pin down the allowed ranges due to the uncertainties on the reaction rates. The reduced efficiency of proton captures on 17O nuclei shown by the new THM reaction rates leads to an increase of the 17O/16O equilibrium value by about 30% at T ≃ 5 × 107 K, with respect to what was obtained with previous data, while the 16O abundance is untouched by extra-mixing phenomena.
Figure 8. 17O/16O isotopic ratio as a function of the temperature T9 in unit of 109 K (solid lines). Equilibrium values computed by using the recommended values of the 17O(p, α)14N and 17O(p, γ)18F reaction rates from Chafa et al. (2007) are given in black, the ones obtained with the rates in the present work are shown in red. Uncertainties due to upper and lower limits of these rates are expressed by short-dashed lines.
Download figure:
Standard image High-resolution imageFigure 9 illustrates the ratio of the 17O mass fraction, calculated by taking the 17O + p rates of Chafa et al. (2007) (X(17O)CHAFA) and of the present work (X(17O)THM), as a function of time from the onset of the AGB phase, in the most efficient extra-mixing case we considered for the 1.2 M☉ AGB ( and Δ = 0.1, case (b) in Figure 7). Adopting the value for and recommended in this work, the 17O depletion is reduced by 25% and by 4%, respectively, in comparison with the results obtained by considering the reaction rates from Chafa et al. (2007). By contrast, the uncertainty range, delimited by the short-dashed lines, is comparable in the two cases. The changes in 14N and 18O abundances due to the different reaction rates are instead negligible.
Figure 9. Temporal evolution of 17O mass fraction in the envelope of a 1.2 M☉ AGB model calculated using the THM 17O + p rates with respect to the mass fraction obtained from the Chafa et al. (2007) rate (red solid line). For comparison, the 17O mass fraction with Chafa et al. (2007) rate is also given as a black solid line (in this scale, equal to one over the whole time interval). The red and black short-dashed lines highlight the range permitted by the uncertainties affecting the reaction rates. All the calculations were performed for the most efficient extra-mixing case reported in Figure 7 (Δ = 0.1 and , case (b)).
Download figure:
Standard image High-resolution imageBack to Figure 7, one can notice that equilibrium values of the 17O/16O isotopic ratio are larger because of the smaller cross sections of the 17O + p reactions. As a consequence, the extra-mixing calculation performed by means of the TH reaction rate (red curves in Figure 9) better describes the behavior of the 17O/16O values from group 2 grains with respect to those obtained by using the rates of Chafa et al. (2007; black curves in Figure 7). Moreover, for stars with masses ⩽1.5 M☉, 17O-burning through proton capture is less efficient than its enrichment, thus the upper mass limit for group 2 progenitors should be further reduced from 1.5–1.7 M☉ (Palmerini et al. 2011b) to 1.2–1.5 M☉, all the grains with 17O/16O ⩽ 0.0013 being reproduced by extra-mixing models applied to an AGB of 1.2 M☉ and solar metallicity. However, we cannot exclude a contribution to group 2 oxide grains from stars with masses larger than about 1.5 M☉, even if this model represents a peculiar case of perfect equilibrium between 17O production and destruction through p-capture and so no changes in its supply can be accounted for by our extra-mixing model. Finally, extra-mixing during the long RGB and the brief AGB phase of a 1 M☉ star might explain the composition of the small population of group 2 (and part of group 1) grains showing a low 17O/16O ratio, as demonstrated in Figure 7 by means of the two short-dashed lines. In these stars, due to the low temperature of the radiative region, the differences due to nuclear physics input (black and red curves) are less appreciable.
The above results agree with the ones by Palmerini et al. (2011b): Very low mass (⩽1.5 M☉) AGB stars affected by efficient extra-mixing phenomena are suitable progenitors of group 2 oxide grains and ∼1 M☉ stars are a suitable environment for the formation of grains poor in 17O and 18O. These grains were considered to populate a "forbidden region" (the one marked with G in Figure 6), which was not accessible by using the cross sections then available (Nollett et al. 2003). The decrease in the 14N(p, γ)17O reaction rate as well as the updated 17O + p results in Adelberger et al. (2011) allow model predictions to spread over the "forbidden region," as displayed by the blue area in Figure 6, and it has been confirmed by the new nuclear physics inputs discussed in this work, leading to the area encircled by the red line in Figure 6. In the same way, grains with 17O/16O ≳ 0.001 can be accounted for using such updated nucleus physics input (especially the 17O(p, γ)18F and 17O(p, α)14N reaction rates, both recommended by Adelberger et al. 2011 and in this work), a range not accessible by Nollett et al. (2003) because of the Angulo et al. (1999) reaction rates in their calculations. Finally, the use of THM reaction rates results in a general reduction of the mass of progenitors of oxygen presolar grains of AGB origin, as efficient extra-mixing applied to a 1.2 M☉ AGB model is necessary (case b of Figure 7), while a 1.5–1.7 M☉ progenitor was required by Palmerini et al. (2011b). A reduction of progenitor masses also implies a reduction of the temperature of the radiative layers crossed by the mixed materials; therefore, the explanation of 26Al/27Al isotopic ratios higher than 0.01 found in some grains becomes much more difficult. Such an enrichment in 26Al is actually possible only if mixing reaches stellar layers with temperature higher than log T ∼ 7.5, but in very low mass AGB stars this temperature is achieved only in the H-burning shell and a mixing so deep might fatally affect stellar energy balance. Anyway, 26Al-rich group 2 grains could form in a progenitor with mass ⩽1.2 M☉ if the 25Mg(p, γ)26Al is much more efficient at log T ⩽ 7; this should be possible if in a future measurement the strength of the resonance at 53 keV is found to be larger than presently accepted.
8.1.2. SiC Grains
In the above scenario, where extra-mixing strongly contributes to the composition of oxide grains, no significant changes in the resulting oxygen isotopic mix derive from the newly estimated 18O(p, α)15N reaction rate, which should be attributed to the 17O + p reactions. Since this reaction is the main 18O depleting channel and, more importantly, the principal 15N production channel, consequences of this new nuclear physics input on nitrogen nucleosynthesis have been analyzed.
A 2 M☉ and solar-metallicity AGB model star has been assumed as progenitor for SiC grains and several extra-mixing cases have been computed attempting to reproduce the composition of Mainstream and A+B SiC grains. Results are shown in Figure 10. Carbon and nitrogen initial isotopic ratios in the envelope of the considered stellar model are fixed by the FDU and evolve under the effect of extra-mixing and TDU episodes, occurring during the AGB phase and conferring a step-wise trend to isotopic ratio lines. Each TDU episode enriches the stellar surface in 12C, increasing the 12C/13C ratio. This ratio is then decreased by the addition of matter processed by extra-mixing in the interpulse period, as suggested in earlier studies in the literature. Four typical extra-mixing cases are demonstrated in Figure 10, where red lines represent the model during C-rich phases, when SiC grains might be formed, while the C/O ratio is lower than 1 along the black tracks. The two dashed lines limit the area of C and N isotopic ratios that can be accounted for by different extra-mixing scenarios, obtained by varying the parameters and Δ in the whole range of allowed values. The four step-wise curves have Δ = 0.2 and from 0.03 to 1 (from right to left). Under the hypothesis that extra-mixing efficiency decreases as the stellar mass increases (Palmerini et al. 2011b), the mixing parameters adopted in the 2 M☉ AGB star case are less deep and have a lower mixing rate than those chosen for the 1.2 M☉ model.
Figure 10. 14N/15N ratios in SiC grains recovered from pristine meteorites, as a function of their 12C/13C ratios. Solid circles represent the A + B grains, open symbols represent the so-called Mainstream ones (WUSTL Presolar Database: http://presolar.wustl.edu/~pgd/). The two symbols ♃ and ☉ indicate the values of the nitrogen isotopic ratios found in Jupiter, which we use as initial abundance in our models, and in the Sun. Step-wise model curves describe the temporal evolution of 12C/13C and 14N/15N ratios in the envelope of a 2 M☉ star of solar metallicity, starting from initial values set by the FDU, assuming that both TDU and extra-mixing are operating. The black solid lines refer to the initial parts of the AGB phase, having C/O ⩽ 1, while the later C-rich phases, which are needed to account for the SiC grain formation, are graphed in red. Extra-mixing models with Δ = 0.2 and = 0.03 (a), 0.1 (b), 0.3 (c), and 1 (d) are reported as indicated by the labels, while the dashed black lines delimit the region that might be covered considering deeper extra-mixing models or varying their mixing efficiency in the range . The range of carbon isotopic ratios characteristic of Mainstream grains and of part of the A+B grains is reproduced, but the 14N/15N ratios predicted by the models are always significantly larger than the solar values and overlap only with the largest observed values, corresponding to the upper fraction of grains. Nucleosynthesis calculations reported in this plot assume the 18O(p, α)15N reaction rate presented in this work. Indeed, changes in the resulting isotopic ratios, due to different nuclear physics input, cannot be appreciated in the logarithmic scale of this plot.
Download figure:
Standard image High-resolution imageDespite the changes in the reaction rates proposed here using the THM approach, only the portion of grains with large 14N/15N isotopic ratios are matched by the nucleosynthesis models. Changes attributable to the new 18O(p, α)15N reaction rate are very small and the challenging scenario described by Nollett et al. (2003) and Palmerini et al. (2011b) is confirmed by the present calculations. Figure 11 displays what changes on 15N and 18O abundances are caused during the AGB phase by the updated reaction rates discussed in the present work. Modifications of the 18O abundance are of the order of ∼10−5 with respect to Angulo et al. (1999) because 18O is very fragile and so easily destroyed that even an increase of about 30% of the 18O(p, α)15N rate, its most important destruction channel, does not produce any appreciable variation. The resulting increase in 15N production is also negligible, 15N being mostly synthesized through the 14N(p, γ)15O(β+)15N chain. Even if the 14N(p, γ)15O reaction rate per particle pair is smaller by at least a factor of 10 than the one of the 18O(p, α)15N reaction, the 14N abundance is so large compared with the 18O one (by more than three orders of magnitude in stellar layers where extra-mixing occurs, as it is shown in Figure 12) that the 14N(p, γ)15O channel proves the dominant one. After the FDU, the 14N/15N isotopic ratio in the envelope of Population I RGB stars with masses between 1.5 and 2.5 M☉ spans the 750–1900 range, while the 14N/18O values are rather smaller, lying in the 180–300 interval (from the FRUITY database: http://fruity.oa-teramo.inaf.it/), thus 18O burning to 15N could account for the lower nitrogen isotopic ratios found in SiC grains. However, 18O abundance is greatly depleted by extra-mixing during the RGB and AGB phases, as discussed for slightly less massive stars (Palmerini et al. 2011b).
Figure 11. As in Figure 9, the temporal evolution of 18O (upper panel) and 15N (lower panel) mass fractions, calculated with the new reaction rates given here and normalized to the ones obtained with standard nuclear physics input (Angulo et al. 1999), are shown. Computation were performed assuming a 2 M☉ AGB model and that most efficient extra-mixing case reported in Figure 10 (Δ = 0.2 and ) is operating. Black lines are used for the standard reaction rates and red lines for the updated nuclear physics input; solid lines show the recommended values and short-dashed lines show the upper and lower limits. Changes of the order of few 10−5 are apparent.
Download figure:
Standard image High-resolution imageFigure 12. (a) Distribution of the 13C, 14N, 15N, and 18O abundances in the radiative layer between the H-burning shell and the convective envelope of a 2 M☉, solar-metallicity model. The stellar radius increases moving toward the outer stellar layers from left to right. This chemical composition has been computed as for Figure 6 of Palmerini et al. (2011b), but considering the reaction rate for proton-capture reaction on 17O and 18O discussed above. The plot is taken roughly at mid-AGB evolution. The two vertical dotted lines and the dashed one indicate the places where Δ = 0.1 and 0.2, and TH, respectively. (b) Trends of proton-capture reactions involved in 14N and 15N nucleosynthesis in the same stellar layers reported in the upper panel. The rates of the (p, γ) and (p, α) reactions on oxygen isotopes are those presented in the previous sections, while the other ones are from Adelberger et al. (2011). Dashed lines show upper and lower limits of the 17O(p, α)14N and 18O(p, α)15N reaction rates.
Download figure:
Standard image High-resolution imageIn the course of the AGB stage, 18O burning sets off at T ⩾ 3 × 107 K, as it is demonstrated in panel (a) of Figure 12, showing the composition of the radiative region between the H-burning shell and the base of the envelope of a 2 M☉ and solar-metallicity AGB star. At this temperatures, the synthesis of 14N via 13C(p, γ)14N and 17O(p, α)14N is also efficient and then both 14N and 15N are produced and enriched in the stellar envelope if extra-mixing is at play. The production of 14N is much more efficient (at least by a factor of 3, up to 100) than the production of 15N through the 14N(p, γ)15O and 18O(p, α)15N channels.
In our extra-mixing scenario, there is not a set of extra-mixing parameters that might account for the reduction of the 14N/15N ratio needed to explain the low values found in many SiC grains. Furthermore, between the H-burning shell and the base of the envelope, there is no layer where the 14N/15N ratio is smaller than ∼1500, for this reason a pure mixing phenomenon is unable to account for depletion of the nitrogen isotopic ratio. In principle, in the inter-shell region of AGB stars a reservoir of 13C and 14N exists. Proton and neutron captures on the latter nucleus generate 15N at the onset of the thermal pulse, by the activation of the 18O(p, α)15N reaction, but it is not expected to be ejected because it is subsequently destroyed in the He convective burning. Even using the updated and revised reaction rates, no solution to the problem of nitrogen in Mainstream and A + B grains can be given.
Concerning A + B grains, the low 14N/15N and 12C/13C values are difficult to explain with extra-mixing phenomena at play both during the RGB and the AGB stages. Extra-mixing might dilute the 12C/13C ratio down to 4–5, but in this case the C/O⩾1 condition, needed for the formation of SiC grains, is not achieved. Values of 12C/13C < 4 cannot be attained anyway, while part of A + B grains has 2 ⩽ 12C/13C ⩽ 4. Hence, C(N)-AGB stars do not appear to be reliable progenitors of A + B grains and other formation sites have to be investigated, a possible candidate being peculiar objects such as CJ-stars and born-again giants like Sakurai's Objects (Amari et al. 2001).
9. CONCLUDING REMARKS
In this work, we have investigated the effect of the recent THM measurement of the 17O(p, α)14N and 18O(p, α)15N low-energy cross sections on astrophysics, in particular, on nitrogen and oxygen isotopic abundances in RGB and AGB stars. The effect of the 17O(p, γ)18F reaction has also been examined in the view of the revised strength of the 65 keV resonance. CNO isotope supply is very sensitive to extra-mixing phenomena, significantly altering their surface abundance. Strong constraints can be set on models using the observed isotopic ratios in circumstellar condensates found in meteorites. Assuming the extra-mixing model presented in Wasserburg et al. (1995), Nollett et al. (2003), and Palmerini et al. (2011b; see Appendix B for details), the coupled CNO nucleosynthesis has been followed, alternatively introducing into the post-processing codes the THM reaction rates and the ones in the literature (Adelberger et al. 2011; Angulo et al. 1999; Chafa et al. 2007).
The change in the 18O(p, α)15N reaction rate stemming from the revised 20 keV resonance strength does not significantly influence either 15N or 18O abundances, 18O being easily destroyed by proton-capture reactions. For this reason, the introduction of this newly measured cross section into our extra-mixing calculations confirms that the low 14N/15N isotopic ratios found in A + B and Mainstream SiC grains have no nuclear reaction origin related to the 18O(p, α)15N channel. Nitrogen isotopic ratios lower than 1000 in SiC grains remain unexplained by the current AGB nucleosynthesis models and possible solutions to the problem have to be investigated. A candidate explanation suggested by Nollett et al. (2003) is that initial values in progenitor stars were much lower than solar, or grain contamination due to cosmic-ray spallation, where 15N is abundantly produced.
The reduced efficiency of proton captures on 17O nuclei given by the new THM reaction rates shows that an increase of the 17O/16O equilibrium values by about 30% is obtained with respect to the literature. This leads to a better agreement between predicted 17O/16O isotopic ratios and experimental values retrieved from group 2 oxide grains. In particular, grains with 17O/16O ≳ 0.001 can be accounted for using the updated nucleus physics input, especially the 17O(p, γ)18F and 17O(p, α)14N reaction rates, both recommended by Adelberger et al. (2011) and in this work. Therefore, extra-mixing calculations performed with the TH reaction rates strengthen the idea that those grains were formed in the envelope of low-mass AGB stars. According to the present work, the upper limit for the progenitor mass should be reduced to 1.2–1.5 M☉ from 1.5–1.7 M☉ as revised by Palmerini et al. (2011b), 17O/16O ⩽ 0.0013 being well reproduced by extra-mixing models applied to an AGB star of 1.2 M☉ and solar metallicity. Finally, the removal of the "forbidden" region in the 17O/16O versus 18O/16O space is a substantial contribution of this work. Such a region is spanned by models assuming that extra-mixing has occurred in a ∼1 M☉ AGB star that has undergone extra-mixing also during the previous longer RGB stage, and introducing into calculations updated 17O + p rates in the place of Angulo et al. (1999) ones.
The work was supported in part by the Italian MIUR under grant No. RBFR082838. S.P. acknowledges support from Spanish Grant AYA2011-22460.
APPENDIX A: SUMMARY OF THE THM FORMALISM IN THE CASE OF RESONANCE REACTIONS
The modified R-matrix approach has been introduced (Mukhamedzhanov et al. 2008; La Cognata et al. 2009a, 2010a, 2010b; Mukhamedzhanov 2011) to extract the physical information of interest from the QF reaction yield, given by the reduced γ-widths in the case of resonance reactions:
for the ith resonance and the τth channel, with Γiτ partial width and the penetration factor for an orbital angular momentum li, or by their combination in the resonance strength:
where Ji, Jx, and JA are the spins of the ith resonance of the compound system B, and ΓixA, ΓicC, and Γitot are the corresponding partial widths for the entrance and the exit channel and the total widths, respectively.
The resonance strength and the resonance energy Ei are the only nuclear parameters needed to calculate the reaction rate in the case of narrow resonances, namely, in the case Γtot ≪ Ei (Rolfs & Rodney 1988; Iliadis 2007). In the resonance THM approach, a HOES resonance strength is deduced, which has to be corrected to account for the virtual nature of the impinging particle (La Cognata et al. 2008a, 2010b). The measured HOES resonance strength of the ith level is given by
where is the cross section for the transfer process A(a, Bi)s, leading to the population of the ith resonance of the compound system B. A proportionality factor used as the THM cross section is measured in arbitrary units, as better accuracy can be obtained through an alternative normalization procedure discussed later. The calculated factor linking the HOES resonance strength to the OES one is (La Cognata et al. 2008a, 2010b)
the sp index denoting that the quantities in the formula are obtained in a simple single particle approach (shell model). Thus,
In a naive sketch, since the A(x, c)C reaction takes place inside the nuclear field, the Coulomb barrier being overcome by hiding x inside a, the entrance channel penetration factor is missing from the resonance strength and so it has to be restored before comparing it with the OES one. In the plane wave impulse approximation (PWIA), the cross section is easily calculated, strongly limiting the number of model parameters, though only the trend of the cross section is retrieved as the absolute value can largely depart from the measured one. Normalization is achieved by equating the strengths of the same resonance measured in direct and in indirect way, for instance, a resonance lying at high energy, such that it can be accurately observed in direct measurements. The normalized resonance strength is
where the index 0 labels a zeroth resonance of strength (ωγ)0, known from direct reactions. This normalization formula above, though relying on direct data thus being affected by the same uncertainty budget, has two main strong points. The peak in the cross section used in the normalization is absolutely arbitrary, so the one having the most accurately measured resonance strength can be chosen, for instance, one for which several concurring measurements are available. Moreover, since the ratio of the Ni factors for two resonances shows up in the equations, the HOES correction factor model dependence is strongly reduced. For instance, the change on the OES strength due to a variation of the channel radius does not exceed 5% for a reasonable change of ±1 fm (La Cognata et al. 2008a, 2010b).
In the case of broad resonances, Γtot ∼ Ei, the energy dependence of the partial widths cannot be neglected and the full HOES R-matrix formalism has to be used to deduce the reduced γ-widths from the THM cross section (La Cognata et al. 2009a, 2010a). In nuclear astrophysics, R-matrix is widely used to extrapolate the S(E)-factor of reaction of astrophysical importance, as it provides a theoretical scheme to describe the cross section (see Lane & Thomas 1958, Barker 2002, Descouvemont & Baye 2010, and Descouvemont et al. 2004, for instance). Moreover, it is a precious tool used to extract the spectroscopic information of reaction cross section, in particular, the resonance partial widths and the corresponding reduced γ-widths. Therefore, it has been proposed to modify the R-matrix to account for the HOES nature of the A(x, c)C reaction. In the modified R-matrix framework, assuming that the rearrangement reaction A(x, c)C proceeds via isolated non-interfering resonances so that a two-level, one-channel R-matrix formula applies, the cross section of the THM reaction can be written as (La Cognata et al. 2011; Mukhamedzhanov 2011)
in the PWIA approach. Here, NF is a normalization factor, (Q is the Q-value of the A(x, c)C reaction, ExA the x−A-relative energy), RxA and RcC the channel radii for the entrance and exit channels, respectively,
where is the spherical Bessel function, (Bxs the binding energy of the a = x⊕s system), and BixA an arbitrary boundary condition chosen to yield the observable resonance parameters (La Cognata et al. 2010a; Mukhamedzhanov et al. 2008, 2011b). Finally, Di(ExA) is the standard R-matrix denominator in the case of two-level, one-channel R-matrix formulae, containing shift and penetration functions besides the boundary conditions set as above (La Cognata et al. 2011). By introducing the level matrix D (Mukhamedzhanov et al. 2008; La Cognata et al. 2010a), a similar equation can be obtained in the two-level, two-channel case, taking into account interference effects. In general, however, a different inference pattern is obtained, as a different mechanism for the population of the resonance states is acting in the THM approach, the M-factor in Equation (A8) entering the R-matrix expression in the place of the entrance-channel penetration factors.
In the modified R-matrix approach, the same reduced widths appear as in the OES S(E)-factor, the only difference being the absence of any Coulomb or centrifugal penetration factor in the entrance channel, which are responsible for the cross section reduction at low energies (La Cognata et al. 2011). From the fitting of the experimental THM cross section through Equation (A7), the reduced widths γiτ can be obtained and used to deduce the OES astrophysical factor, which turns out to be not affected by the electron screening nor by experimental energy resolution, broadening the experimental resonances. As in the narrow resonance case, normalization is achieved by extending the indirect measurement to an energy region where directly measured resonances are available and scaling the deduced γ-widths to match the values in the literature. The presence of the M-factor of Equation (A8) renormalizing each resonance makes a single normalization constant necessary for the whole investigated energy region. Finally, the ration rate is computed by folding the astrophysical S(E)-factor including the experimental reduced widths with the Maxwell–Boltzmann velocity distribution (Rolfs & Rodney 1988; Iliadis 2007).
APPENDIX B: ESSENTIAL FEATURES OF THE EXTRA-MIXING MODEL
The adopted extra-mixing model is the parametric one presented in Palmerini et al. (2009, 2011a, 2011b) and Busso et al. (2010). It is "two-stream conveyor belt" circulation model as the one proposed by Wasserburg et al. (1995) and Nollett et al. (2003), but implemented into a recently developed program run as a post-process of the FRANEC stellar evolutionary code, as modified by Cristallo et al. (2009). Such a "two-stream conveyor belt" circulation model contains two free parameters: the mixing rate that we express in units of 10−6 M☉ yr-1 and the mixing depth Δ, which is given by the difference Δ = log TH − log TP, TH being the temperature at which the energy production in the H-burning shell is maximum and TP the temperature of the deepest layer reached by mixing. In such a slow-mixing framework, where no assumptions have been made on the physical mechanism generating the mass transport, the mixing velocity is related to the mixing rate through the relation
where f = 0.5 being the fractional areas occupied by the upward and downward mass transport (see Busso et al. 2010; Nollett et al. 2003, for details). Since a small amount of nuclear processing takes place in the circulating material (Nollett et al. 2003), computing extra-mixing generally calls for a description of nuclear physics phenomena coupled with mass transport. This can be obtained by solving a system of differential equations of the type (Palmerini & Busso 2008)
where Yi is the abundance by mole of the ith isotope; m and r the mass and radius coordinates along the stellar radiative layer; the partial derivative with respect to time describes the abundance changes due to nucleosynthesis; finally, the second term of the right-hand side deals with the displacement across the radiative region.
In the slow-mixing framework, the composition changes due to extra-mixing can be followed in a simpler way, which does not require one to solve Equation (B2). Hence, nucleosynthesis results are deduced resorting to the path integral of reaction rates over trajectory, an approach similar to the one adopted by Wasserburg et al. (1995), who integrated the burning rate over mass through the path. Following the same procedure of Busso et al. (2010) and Palmerini et al. (2011b, 2011a), we calculate the evolution of the isotopic composition in the parcel of transported material (in a Lagrangian framework) by integrating a set of equations (one for each isotope i):
where is the abundance of a stable, or long-lived, parent of nucleus i, producing it through p-captures in a parcel of transported material; is an unstable parent of nucleus i, producing it through weak interaction (β± decays or e− captures); is the rate for the corresponding weak interaction process leading to i. A similar definition applies to λi (in this case for destroying i). Ri,H and indicate the reaction rates for proton-capture reactions on nucleus i and pi,s, respectively, and their values depend on the temperature T and the density ρ of the crossed stellar layers, which are functions of the position within the radiative zone. The abundance the ith isotope in the stellar envelope (Yenvi,0) is assumed as the initial value for Yi. The composition of the material reaching the convection interface Ymixi is calculated by integrating Equation (B3) over time (for the interval of time spent by a parcel of material to proceed along the whole circulation path, δτmix). The time a parcel of mixed material takes to cross each layer of the radiative region is fixed by Equation (B1) and the reaction rate values R (or λ) are calculated along the path for the specific T and ρ values.
Therefore, the envelope isotopic composition Xenvi resulting from the mixing is calculated as7
where is the mixed mass in the time interval spent by a parcel of transported material to complete its path along the radiative region and Menv is the mass of the stellar envelope. Once that the new envelope composition has been computed it is assumed as the initial one for other transported material, and the calculation is repeated iteratively to evaluate the evolution of the stellar envelope composition due to extra-mixing during the RGB phase or each inter-pulse period of the AGB stage.
Footnotes
- 5
- 6
Since x is virtual, the (non-relativistic) mass–shell equation Ex = p2x/2mx is not satisfied, that is, x is off-energy-shell. Since c−C are real particles, they fulfill the mass–shell equation. Therefore, the cross section is HOES, as only in the entrance channel the mass-shell relation is violated. In the case of direct measurements, both entrance and exit channels contain real particles thus the cross section is OES.
- 7
The abundance by mass Xi of a nucleus i and the one in number per mole Yi are related by its atomic mass trough the relation Yi = (Xi/Ai).
- Adande G. R. and Ziurys L. M. 2012 ApJ 744 194
- Adelberger E. G., García A., Robertson R. G. H. et al. 2011 RvMP 83 195
- Amari S., Nittler L. R., Zinner E., Lodders K. and Lewis R. S. 2001 ApJ 559 463
- Angulo C., Arnould M., Rayet M. et al. 1999 NuPhA 656 3
- Asplund M., Grevesse N., Sauval A. J. and Scott P. 2009 ARA&A 47 481
- Assenbaum H. J., Langanke K. and Rolfs C. 1987 ZPhyA 327 461
- Barker F. C. 2002 NuPhA 707 277
- Baur G. 1986 NuPhA 458 188
- Blackmon J. C., Champagne A. E., Hofstee M. A. et al. 1995 PhRvL 74 2642
- Boothroyd A. I. and Sackmann I.-J. 1999 ApJ 510 232
- Boothroyd A. I., Sackmann I.-J. and Wasserburg G. J. 1995 ApJL 442 L21
- Brown R. E. 1962 PhRv 125 347
- Busso M., Palmerini S., Maiorca E. et al. 2010 ApJL 717 L47
- Chafa A., Tatischeff V., Aguer P. et al. 2007 PhRvC 75 035810
- Champagne A. E. and Pitt M. 1986 NuPhA 457 367
- Charbonnel C. and Lagarde N. 2010 A&A 522 10
- Christensen N. S., Jensen F., Besenbacher F. and Stensgaard I. 1990 NIMPB 51 97
- Cristallo S., Piersanti L., Straniero O. et al. 2011 ApJS 197 17
- Cristallo S., Straniero O., Gallino R. et al. 2009 ApJ 696 797
- Descouvemont P., Adahchour A., Angulo C., Coc A. and Vangioni-Flam E. 2004 ADNDT 88 203
- Descouvemont P. and Baye D. 2010 RPPh 73 036301
- Fiorentini G., Kavanagh R. W. and Rolfs C. 1995 ZPhyA 350 289
- Fouchet T., Irwin P. G. J., Parrish P. et al. 2004 Icar 172 50
- Fouchet T., Lellouch E., Bézard B. et al. 2000 Icar 143 223
- Fox C., Iliadis C., Champagne A. E. et al. 2004 PhRvL 93 081102
- Fox C., Iliadis C., Champagne A. E. et al. 2005 PhRvC 71 055801
- Gerin M., Marcelino N., Biver N. et al. 2011 A&A 498 L9
- Gulino M., Spitaleri C., Cherubini S. et al. 2010 JPhG 37 125105
- Harris M. J. and Lambert D. L. 1984 ApJ 285 674
- Herwig F. 2005 ARA&A 43 435
- Huss G. R., Hutcheon I. D. and Wasserburg G. J. 1997 GeCoA 61 5117
- Huss G. R., Hutcheon I. D., Wasserburg G. J. and Stone J. 1992 Press Abstracts for the Twenty-third Lunar and Planetary Science Conference (Houston: TX: Lunar and Planetary Institute) 29
- Iliadis C. 2007 Nuclear Physics of Stars (Weinheim: Wiley-VCH Verlag)
- Iliadis C., Angulo C., Descouvemont P., Lugaro M. and Mohr P. 2008 PhRvC 77 045802
- Iliadis C., Longland R., Champagne A. E. and Coc A. 2010 NuPhA 841 251
- José J. and Hernanz M. 2007 JPhG 34 R431
- Kahane C., Cernicharo J., Gomez-Gonzalez J. and Guelin M. 1992 A&A 256 235
- Kieser W. E., Azuma R. E. and Jackson K. P. 1979 NuPhA 331 155
- La Cognata M., Goldberg V. Z., Mukhamedzhanov A. M., Spitaleri C. and Tribble R. E. 2009a PhRvC 80 012801
- La Cognata M., Mukhamedzhanov A. M., Spitaleri C. et al. 2011 ApJL 739 L54
- La Cognata M., Romano S., Spitaleri C. et al. 2006 EPJA 27 249
- La Cognata M., Romano S., Spitaleri C. et al. 2007 PhRvC 76 065804
- La Cognata M., Spitaleri C. and Mukhamedzhanov A. M. 2010a ApJ 723 1512
- La Cognata M., Spitaleri C., Mukhamedzhanov A. M. et al. 2008a PhRvL 101 152501
- La Cognata M., Spitaleri C., Mukhamedzhanov A. M. et al. 2009b PASA 26 237
- La Cognata M., Spitaleri C., Mukhamedzhanov A. M. et al. 2010b ApJ 708 796
- La Cognata M., Spitaleri C., Tribble R. E. et al. 2008b JPhG 35 014014
- La Cognata M., Spitaleri C., Tumino A. et al. 2005 PhRvC 72 065802
- Lamia L., Romano S., Carlin N. et al. 2007 NuPhA 787 309
- Lamia L., Spitaleri C., Carlin N. et al. 2008 NCimC 31 423
- Lamia L., Spitaleri C., La Cognata M., Palmerini S. and Pizzone R. G. 2012 A&A 541 A158
- Landre V., Aguer P., Bogaert G. et al. 1989 PhRvC 40 1972
- Lane A. M. and Thomas R. G. 1958 RvMP 30 257
- Lorenz-Wirzba H., Schmalbrock P., Trautvetter H. P. et al. 1979 NuPhA 313 346
- Lugaro M., Karakas A. I., Nittler L. R. et al. 2007 A&A 461 657
- LUNA Collaboration, Lemut A., Bemmerer D. et al. 2006 PhLB 634 483
- Mak H.-B., Evans H. C., Evan G. T. and MacArthur J. D. 1978 NuPhA 304 210
- Marty B., Chaussidon M., Wiens R. C., Jurewicz A. J. G. and Burnett D. S. 2011 Sci 332 1533
- Moazen B. H., Bardayan D. W., Blackmon J. C. et al. 2007 PhRvC 75 065801
- Mukhamedzhanov A. M. 2011 PhRvC 84 044616
- Mukhamedzhanov A. M., Blokhintsev L. D., Irgaziev B. F. et al. 2008 JPhG 35 014016
- Mukhamedzhanov A. M., La Cognata M. and Kroha V. 2011 PhRvC 83 044604
- Newton J. R., Iliadis C., Champagne A. E., Longland R. and Ugalde C. 2007 PhRvC 75 055808
- Nittler L. R. 2009 PASA 26 271
- Nittler L. R., Alexander C. M. O'D., Gao X., Walker R. M. and Zinner E. 1997 ApJ 483 475
- Nollett K. M., Busso M. and Wasserburg G. J. 2003 ApJ 582 1036
- Owen T., Mahaffy P. R., Niemann H. B., Atreya S. and Wong M. 2001 ApJL 553 L77
- Palmerini S. and Busso M. 2008 NewAR 57 7
- Palmerini S., Busso M., Maiorca E. and Guandalini R. 2009 PASA 26 161
- Palmerini S., Cristallo S., Busso M. et al. 2011a ApJ 741 26
- Palmerini S., La Cognata M., Cristallo S. and Busso M. 2011b ApJ 729 3
- Pizzone R. G., Spitaleri C., Cherubini S. et al. 2005a PhRvC 71 058801
- Pizzone R. G., Spitaleri C., Lamia L. et al. 2011 PhRvC 83 045801
- Pizzone R. G., Spitaleri C., Lattuada M. et al. 2003 A&A 398 423
- Pizzone R. G., Tumino A., degl'Innocenti S. et al. 2005b A&A 438 779
- Rolfs C. and Rodney W. S. 1975 NuPhA 250 295
- Rolfs C. and Rodney W. S. 1988 Cauldrons in the Cosmos (Chicago, IL: Univ. Chicago Press)
- Schmidt C. and Duhm H. H. 1970 NuPhA 155 644
- Sharp C. and Wasserburg G. J. 1995 GeCoA 59 1633
- Sergi M. L., Spitaleri C., Coc A. et al. 2010a NuPhA 834 676
- Sergi M. L., Spitaleri C., La Cognata M. et al. 2010b PhRvC 82 032801
- Spitaleri C. 1990 Problems of Fundamental Modern Physics II ed R. Cherubini, P. Dalpiaz and B. Minetti (Singapore: World Scientific) 21
- Spitaleri C., Aliotta M., Cherubini S. et al. 1999 PhRvC 60 055802
- Spitaleri C., Lamia L., Tumino A. et al. 2004 PhRvC 69 055806
- Spitaleri C., Mukhamedzhanov A. M., Blokhintsev L. D. et al. 2011 PAN 74 1763
- Straniero O., Chieffi A., Limongi M. et al. 1997 ApJ 478 332
- Strieder F., Limata B., Formicola A. et al. 2012 PhLB 707 60
- Strieder F., Rolfs C., Spitaleri C. and Corvisiero P. 2001 NW 88 461
- Tumino A., Spitaleri C., Bonomo C. et al. 2005 EPJA 25 649
- Tumino A., Spitaleri C., Mukhamedzhanov A. M. et al. 2011 PhLB 700 111
- Tumino A., Spitaleri C., Sergi M. L. et al. 2006 EPJA 27 243
- Wasserburg G. J., Boothroyd A. I. and Sackmann I.-J. 1995 ApJL 447 L37
- Wen Q.-G., Li C.-B., Zhou S.-H. et al. 2008 PhRvC 78 035805
- Wiescher M., Becker H. W., Görres J. et al. 1980 NuPhA 349 165
- Wiescher M. and Kettner K. U. 1982 ApJ 263 891
- Yagi K. 1962 JPSJ 17 604
- Zinner E. 1998 AREPS 26 147
- Zinner E. 2005 Treatise of Geochemistry I. Meteorites, Comets, and Planets ed A. M. Davis (Amsterdam: Elsevier) 17
- Zinner E., Nittler L. R., Gallino R. et al. 2006 ApJ 650 350