AUTOMATED UNSUPERVISED CLASSIFICATION OF THE SLOAN DIGITAL SKY SURVEY STELLAR SPECTRA USING k-MEANS CLUSTERING

Stellar spectra contain a wealth of information on the photospheres of stars, including their chemical makeup. In spite of decades of measuring and studying stellar spectra, we have a very limited knowledge of how many stars with a given chemical composition exist in the Galaxy. Large spectroscopic surveys such as RAVE (Steinmetz et al. 2006) or the Sloan Digital Sky Survey (SDSS; e.g., Stoughton et al. 2002) have increased by several orders of magnitude the number of stars with measured spectra, yet these surveys are limited in scope, reaching only a particular cross-section of the stellar population of the Milky Way, and biased, in that they target stars that have been preselected based on their color, distance, or brightness. This situation will soon change as new large projects such as Gaia (e.g., Turon et al. 2005) or HETDEX (Hill et al. 2008), with well-controlled samples, appear on the scene. The advent of these new data sets poses an obvious problem. As the data flow continuously increases, performing systematic studies becomes more of an issue, and new efficient means of analyzing stellar spectra are needed.

The study of stellar spectra to quantify the physical properties of stars requires model atmospheres, radiative transfer calculations, atomic and molecular data, and involves a large number of approximations. The model ingredients and our recipes of applying them to interpret observations are in constant evolution, and so are the values for the inferred quantities. Avoiding such changes is one of the motivations behind spectroscopic classification in general, and in particular of the MK system of Morgan et al. (1943) and Morgan & Keenan (1973), which is still in use today enhanced with extensions. It assigns spectral classes in a way that is purely empirical and repeatable, providing basic information as a preliminary step for further, more detailed analysis.

This kind of classification system based on a series of predefined criteria is feasible as long as the criteria are set and applied by humans. Such systems resemble the taxonomical classification of animal species (see Fraix-Burnet et al. 2006) and, by definition, are not optimal since they rely on subjective judgments. If such systems have to be updated for application to very large number of spectra, the classification has to be easily implemented and performed with computers, in a fast and homogeneous fashion. Moreover, Sandage (2005) maintained that physics must not be used to drive a classification; otherwise the arguments become circular when using the classification to support physics. Thus, one is inclined to consider unsupervised classification systems, which are themselves defined by algorithms and data. The potential of one of such methods, k-means, is explored in this paper. However, it must be stressed that unsupervised does not mean absolute or model independent. The classification criteria are implicitly set by the algorithm, and the resulting classes depend on the specific data set under analysis.

In data mining parlance, the spectrum of a star is a point in the high-dimensional space where each coordinate corresponds to the intensity at a particular wavelength. Given a comprehensive set of stellar spectra, classifying consists of identifying clusters in this high-dimensional space. The problem of finding structures in a multidimensional data set goes also by the name of cluster analysis (see, e.g., Everitt 1995; Bishop 2006). One of the most widely used algorithms is k-means clustering (MacQueen 1967), and it fulfills the requirements put forward above. Moreover, k-means is simple to code and robust, even when exploring clustering in a high-dimensional space. Previous works have shown successful applications of the method to the classification of spectra in various astrophysical contexts, e.g., stars (Balazs et al. 1996; Simpson et al. 2012), solar polarization spectra (Sánchez Almeida & Lites 2000; Viticchié & Sánchez Almeida 2011), X-ray spectra (Hojnacki et al. 2007), spectra from asteroids (Galluccio et al. 2008), and galaxy spectra (Sánchez Almeida et al. 2009, 2010; Morales-Luis et al. 2011).

We now explore its application to medium-resolution stellar spectra from the SDSS. SDSS currently provides the largest available homogenous database of stellar spectra. The original SDSS survey (Stoughton et al. 2002; Abazajian et al. 2009) together with SEGUE and SEGUE-2 contain somewhere over half a million stellar spectra (Yanny et al. 2009). The Baryon Oscillations Spectroscopic Survey (Eisenstein et al. 2011), part of SDSS-III, uses similar but upgraded spectrographs, and in the first two years of operation has already obtained over 100,000 additional spectra of stars. Even though these stars do not provide a fair sample of the Milky Way stellar population, this rich data set is a good place to explore the application of clustering algorithms for classifying stars. Actually, the set has already been used for this purpose. McGurk et al. (2010) apply principal component analysis (PCA) to spectra having narrow color bins, so as to separate stars of the same effective temperature according to their gravity and metallicity. In this case the spectra are not classified directly by the automated procedure, but the color cuts introduce human supervision into the classification. Daniel et al. (2011) apply local linear embedding, which is a type of PCA decomposition that preserves the nonlinear structure within high-dimensional data sets. The stellar spectra are found to form a one-dimensional family when projected into the first three eigenvectors. Finally, Asensio Ramos & Allende Prieto (2010) also use SDSS data to show that stellar spectra are highly compressible, so that a small number of parameters suffice to reproduce the bulk of the observed spectra.

In this paper, we focus on the k-means classification of stars observed as part of the SEGUE and SEGUE-2 surveys (Yanny et al. 2009). Section 2 presents the selection of spectra used in the analysis, and Section 3 describes the basics behind k-means. Section 4 applies the algorithm to SDSS spectra, first considering continuum (Section 4.1), and then without continuum (Section 4.2). The classification allows us to identify outliers, often rare objects that do not show up unless the catalogs are large enough and which turn out to be extremely revealing (e.g., Matijevič et al. 2012). The properties of these outliers are analyzed in Section 5. Section 6 explains the main results and outlines additional uses of the classification.

The spectra come from SEGUE and SEGUE-2 (Yanny et al. 2009). These programs obtained stellar spectra using the SDSS 2.5 m telescope and the SDSS double spectrograph (Gunn et al. 2006; Smee et al. 2012) between 2004 and 2009. The spectra contain 3849 wavelengths covering the range 3800–9200 Å at a resolving power R ≃ 1800. They were downloaded from the SDSS Data Release 8 (DR8; Aihara et al. 2011). SEGUE observed numerous types of targets, from very hot white dwarf (WD) to very cool M and L types, each chosen based on color criteria, and in some cases additional information such as proper motion. The survey observations sample the Galaxy at mid- and high-galactic latitudes, covering very sparsely three-fourths of the sky, with only three plates (less than 0.5% of the spectra) at |b| < 10°.

The sample of DR8 spectra associated with SEGUE and SEGUE-2 programs includes 355,840 spectra in 525 plug-plates. Each plate, as for SDSS, admits 640 fibers. We selected stars with a median signal-to-noise ratio S/N > 10, a radial velocity module smaller than 600 km s⁻¹ (redshift <0.002), and which were not labeled as one of the following classes of objects: GALAXY, NA, QA, ROSAT_D, QSO, SER, and CATY_VAR.

We processed the spectra to eliminate by interpolation the [O iii] nightglow lines at 5577 and 6300 Å, and corrected the Doppler shifts associated with the radial velocities. The original spectra have units of flux per unit wavelength (i.e., erg cm⁻² s⁻¹ Å⁻¹). We normalized them, dividing by the median value of their fluxes in the spectral band between 5000 and 6000 Å. This step preserves the shape of the spectral energy distribution while placing all the spectra on the same scale regardless of the intrinsic luminosity of the stars, their distance, and the amount of interstellar absorption. Missing sections of spectra were patched by interpolation, since any regions with extreme (wrong) values can damage the classification algorithm. A sample 173,390 stellar spectra passed all the selection criteria, and we refer to them as the reference set. Interstellar extinction is not corrected for; however, we analyze a version of the same data with a running mean subtracted from the spectral energy distribution, leaving only absorption features. This procedure is intended to partly remove the reddening produced by interstellar extinction, thus minimizing its potential impact on the results.

Two additional sets of spectra are mentioned in the paper. They were used only for testing in early stages of the work, but they are explicitly mentioned here because the sanity checks performed with them provide confidence in the technique. As far as we can tell, they are equivalent to the reference set in a statistical sense. For lack of imagination, we refer to them as 1st auxiliary set and 2nd auxiliary set. Auxiliary set 1 comprises 63,611 stellar spectra from 3800 to 8000 Å, drawn from SDSS/DR6 and then purged to retain only those with best S/N. They are uniformly resampled in log-wavelength as to have 1617 wavelengths. This set is particularly rich in main-sequence F-type stars, since they were used as spectrophotometric calibrators in the original SDSS survey (only 162 distinct SEGUE plates were included in DR6). Auxiliary set 2 comes from DR8, but the noise thresholding and other selection criteria differ from the reference set, and leaves only 121,272 targets.

Effective temperatures T_eff, surface gravities (log  g), and metallicities ([Fe/H]) computed with the SEGUE Stellar Parameter Pipeline (hereafter SSPP; Lee et al. 2008a, 2008b; Allende Prieto et al. 2008; Lee et al. 2011; Smolinski et al. 2011) are used here to characterize the physical properties of the stars. Each one of these physical parameters results from the robust average of various independent estimates, discarding those which do not seem to be consistent (for details, see Lee et al. 2008a). The MK types of the targets mentioned in the paper are also from the SSPP. Most of our discussion is based on the so-called ELODIE MK types, derived by best-fitting templates from the ELODIE library of synthetic spectra (Prugniel & Soubiran 2001). The distribution of MK types of the reference set is shown in Figure 1. These types encompass a broad range of stellar properties from O to L and included WDs; however, they face some difficulties when interpreting intermediate spectral types (e.g., the distribution of MK types in Figure 1 peaks at type F whereas most of the SEGUE stars have been selected to be of G type; see Yanny et al. 2009). The SSPP also provides a second set of MK types only for cool stars, the Hammer MK types, which were inferred using the spectral typing software developed and described by Covey et al. (2007). They cope much better with types G and F, and we apply them when appropriate.

Zoom In Zoom Out Reset image size

We use k-means to carry out the classification, which is a robust tool commonly used in data mining and artificial intelligence (e.g., Everitt 1995; Bradley & Fayyad 1998). The actual realization of the algorithm employed in our analysis is described in detail by Sánchez Almeida et al. (2010, Section 2), and we refer to that work for details. However, for comprehensiveness, this section sketches the operation of the algorithm, with its pros and cons.

As for most classification algorithms, the stellar spectra are vectors in a high-dimensional linear space, with as many dimensions as the number of wavelengths. Therefore the spectra to be classified are a set of points in this space. The points (i.e., the spectra) are assumed to be clustered around a number of centers. Classifying consists of (1) finding the number of clusters and their centers, (2) assigning each spectrum to one of these centers, and (3) estimating the probability that the choice is correct. The third step should be regarded as a sanity check that allows us to quantify the goodness of the classification for each particular spectrum. In the standard formulation, k-means starts by selecting at random from the full data set a number k of spectra. These spectra are assumed to be the center of a cluster. Then each spectrum of the data set is assigned to the cluster center that is closest in a least-squares sense.³ Once all spectra have been assigned to one of the classes, the cluster centers are recomputed as the average of the spectra in the cluster. The procedure is iterated with the new cluster centers, quitting when most spectra are not re-assigned in two successive steps (99% of them in our realization). The number of clusters is arbitrarily chosen, but the results are insensitive to such selection since only a few clusters possess a significant number of members. Thus, the algorithm provides the number of clusters and their corresponding cluster centers, as well as the classification of all the original spectra now assigned to one of the clusters. This information completes steps (1) and (2) of the classification procedure. In order to estimate the probability that the assignation is correct (step 3), we compute for each cluster the distribution of the distances to the cluster center considering all spectra assigned to the cluster. We then assume that this distribution describes the probability that any star with a given distance from the cluster center belongs to the class. Specifically, the probability that a given star belongs to a cluster is estimated as the fraction of stars in the cluster with distances equal to or larger than the distance of the star. It is a sensible assumption; it gives high probability to spectra close to the cluster center, and then drops down smoothly toward the outskirts of the cluster. The scale of this smooth decrease is provided by the measured distribution of distances in the class.

The algorithm is simple, robust, and fast, which makes it ideal to treat large data sets. It guarantees that similar spectra end up in the same cluster. Moreover, it is unsupervised since no prior knowledge of the stellar properties is used, and the spectra to be classified are the only information passed on to the algorithm.⁴ These two properties ensure that the resulting classification is not biased by our (physical) prejudices, which follows the spirit of a good classification as advocated by Sandage (2005). Unfortunately, it also has three major drawbacks. One of them is technical, whereas the other two deal with the physical interpretation of the classes. The algorithm yields different classifications depending on the random initialization. This difficulty is overcome by repeating the classification multiple times, thus studying the dependence of the final classes on the random seeds. In addition, our implementation refines the initialization so that the random seeds are not chosen uniformly but according to the distribution of points in the classification space (for details, see Sánchez Almeida et al. 2010). The second difficulty has to do with interpreting the classes as actual clusters in the classification space or as parts of larger structures. The algorithm does not guarantee that the derived classes correspond to actual clusters. However, one can figure out whether each particular class is isolated or belongs to a larger structure by studying the distances of the spectra in the class to the other classes. Well-defined classes contain stars that are distant from the other classes. The third difficulty refers to the physical interpretation of the resulting classes, which is not provided by the algorithm. The physical sense of a particular class and its cluster center (dubbed the template spectrum in this paper) has to be figured out later on. Actually, most of this paper is devoted to this task, i.e., to interpreting in terms of known stellar physics the classes resulting from the k-means classification.

3.1. Repeatability of the Classification

As is customary, the dependence of the classification on the random initialization was studied by repeating the classification 100 times, and then comparing the results. This internal comparison was carried out using three parameters that we name: (1) coincidence, for the percentage of spectra in equivalent classes; (2) dispersion, for the rms fluctuations of the spectra in a class with respect its cluster center; and (3) number of classes, for the number of classes that contain 99% of the spectra (major classes). In order to decide which classes in two different classifications are equivalent, we compute the number of stars in common between each pair of classes formed by one class from one classification and the second class from the second classification. The two classes sharing the largest number of stars are assumed to be equivalent. The same criterion is repeated until all the classes of one of the classifications have been paired. This criterion maximizes the number of stars sharing the same class in the two classifications.

Figure 2 shows scatter plots of the three diagnostic parameters corresponding to repeated classifications of the reference data set (Section 2) including continuum. One finds classifications having between 15 and 20 major classes, a dispersion in the range 0.07 to 0.08, and a mean coincidence between 62% and 68%. The ranges in these values are fairly narrow. The fact that the coincidence is about 65% means that one can pair the classes of any two classifications, and they will share about 65% of the spectra. (These apparently low values are discussed below.) The fact that the dispersion is of the order of 0.075 implies that the differences between the class template spectra and the spectra in the class are of the order of 7.5% rms. These numbers refer to the reference data set including continua (Section 4.1) but are similar to those obtained when spectra without continua are used (Section 4.2), or when using the auxiliary sets.

Zoom In Zoom Out Reset image size

In addition to the above tests, we conducted a numerical experiment, splitting the 1st auxiliary set into two randomly chosen disjoint subsets, which were classified independently. The differences give an idea of the dependence of the classes on the particular data set that is employed. The results are summarized in Figure 3, which shows the template spectra of equivalent classes in the two classifications. (Only nine classes are included, but they are representative of the general behavior.) The differences between spectra are also plotted, and turn out to be of a few percent, i.e., smaller than the scatter among the spectra included in each class (the dispersion of these classifications was of the order of 5%). We have also computed the colors of the templates and of the individual stars, and the differences between the colors of the templates (∼0.025 mag) are smaller than the scatter among individual stars in a class (∼0.05 mag).

Zoom In Zoom Out Reset image size

As mentioned above, repeating the classification several times leaves only 60%–70% of the spectra in equivalent classes. This issue with k-means is not directly due to the random initialization—the cluster centers in equivalent classes are very similar, as shown in Figure 3 and in Sánchez Almeida et al. (2010, Section 2.1). It is due to the fact that k-means slices a rather continuum distribution. Then small changes in the borders between clusters produce a significant relocation of the in-between stars. The effect is boosted because the clusters are in a high-dimensional space (see the analytic justification in the Appendix of Sánchez Almeida et al. 2010). We show in Section 4.1 how some of the resulting clusters really have many stars near their borders.

The actual classifications were carried out in parallel using several workstations. The reference data set has a volume of 6.1 GB, and the process requires some two CPU hours per single classification, or two hundred hours for studying the effects of the random initialization. These figures are mentioned to stress that the k-means classification of a sizable data set, including studying initial conditions, is easily doable using standard hardware facilities.

The description given in this section refers to the reference set defined in Section 2, however, the same procedures and analysis have been repeated with the two auxiliary sets, always giving consistent results.

The classifications use all the 3849 wavelengths equally weighted. We consider two cases for the analysis. In the first case, the full spectra are used (Section 4.1). In the second, a running average 193 pixels wide (≡17,400 km s⁻¹) is subtracted from each spectrum (Section 4.2). This high-pass filtering removes the continuum but leaves the spectral lines almost untouched.

4.1. Classes with Continuum

In order to study the dependence of the classes on the random seeds inherent to k-means, we carried out 100 independent classifications (Section 3.1). They are equally valid classifications, but we have to choose from among them one to be used as the classification. Taking advantage of having all these possibilities, we try to select the one that is as representative as possible of all of them, the spectra in their classes are as similar as possible, and has the smallest number of classes. In the parlance used in Section 3.1, we try to select a classification having large coincidence, small dispersion, and few classes. The scatter plots for these three parameters among the 100 independent classifications are shown in Figure 2. Asking the coincidence to be larger than 66%, the dispersion to be smaller than 0.074, and the major classes to be fewer than 17, one finds only two classifications. Those are represented as asterisks in Figure 2. For the lack of a better criterion, we choose one of them at random. Its coincidence is 67%, its dispersion is 0.073, and it has 16 major classes (26 in total, but some seem to correspond to failures of the SDSS pipeline, as we explain later on).

The average of all the spectra in the classes (i.e., the cluster centers or the cluster templates) is shown as solid lines in Figure 4. The figure also includes the standard deviation among all the spectra in each class (the dotted line), which quantifies the intraclass dispersion. The number of stars in each class is represented as a histogram in Figure 5. It shows that the classes have been numbered according to the stars than contain, being class 0 the most numerous, class 1 the second-most numerous, and so on and so forth. Since the template spectra come from averaging thousands of individual spectra, they have extremely high S/Ns—from 200 to 2000 depending on the number of spectra in the class. The spectra of classes 22 and 24 are not included in Figure 4. They collect faulty spectra that are similar to class 17 (see the template spectrum in Figure 4 that has a large unphysical spike at the bluest wavelength). The templates are also represented in Figure 6 as a stack-plot ordered so that the image looks as smooth as possible. This image excludes those classes that are failures of the pipeline (classes 17, 22, and 24) and binary systems (classes 20 and 21; see below).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

As we discuss in Section 3, k-means does not guarantee the inferred classes to be real clusters in the classification space. They may be parts of larger structures that have been sliced by the algorithm. A way to study whether or not the classes are isolated was explored in Sánchez Almeida et al. (2010), and it is used here too. One can estimate the probability that each particular star belongs to the class it was assigned to. It depends on how far from the cluster center the star is as compared to the other members in its class. Similarly, one can estimate the probability of the star belonging to any other class. Well-defined clusters will have most of their elements with a probability of belonging to any other cluster significantly smaller than the probability of belonging to the cluster. Figure 7 shows histograms of the ratios between probabilities of belonging to the second-nearest cluster and to the assigned cluster for a few representative classes. There are classes where the histogram peaks at low ratios, thus indicating a well-defined structure in the classification space (e.g., class 0 in Figure 7). Conversely, other classes present a rather flat histogram indicating a dispersed structure (e.g., class 3 in Figure 7). Classes 3, 5, 11, and 19 represent spreadout classes, whereas the rest are clustered classes. Note, however, that even the histograms of well-defined clusters have a significant tail toward large ratios, indicating the presence of many stars in the boundaries between clusters. Those stars are partly responsible for the non-uniqueness of the classification studied in Section 3.1.

Zoom In Zoom Out Reset image size

The physical interpretation of some of the classes is relatively straightforward. Classes 20 and 21, with upturns in both the blue and the red, are most likely composite spectra of systems with two (or more) stars with very different effective temperatures (T_eff). They can be gravitationally bounded stellar systems or stars that happen to be along the line of sight. The luminosity of the stars that contribute to the combined spectrum has to be similar, therefore, in case of binary systems both stars cannot be in the main sequence because the hot star would outshine any cold companion. One common possibility is a hot WD and a cold dwarf or giant, and this is indeed the conclusion reached when trying to reproduce the templates of classes 20 and 21 as a linear superposition of templates of two other classes. The best fit is obtained by combining classes 16 and 18, as shown in Figure 8. As we discuss later on, class 16 contains WDs, and class 18 corresponds to K-type giants. We note that the templates of classes 20 and 21 resemble spectra of post-common envelope binaries, as identified and studied using SDSS data (e.g., Rebassa-Mansergas et al. 2007, 2008; Schreiber et al. 2008). Some other classes are really awkward, and so are difficult to interpret unless they are associated with failures in the reduction pipeline (e.g., classes 17 and 19).

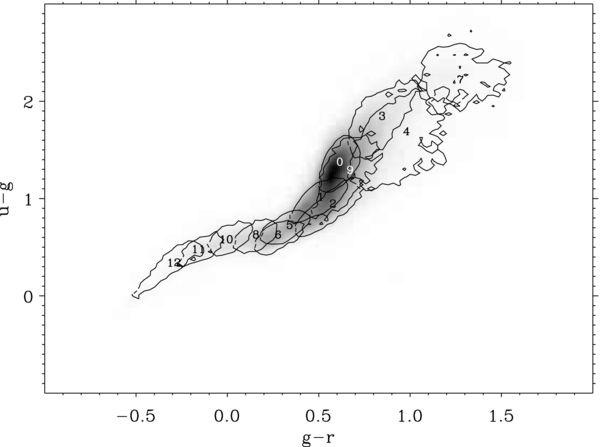
Zoom In Zoom Out Reset image size

Figure 9 shows an image with the distribution of u − g versus g − r colors of the full set, with the individual classes overlaid as contours containing 68% of the stars. The colors have been derived from the spectra using the transmission bandpasses of the broadband SDSS filters. Note that the classification is basically a color classification. Disregarding classes gathering failures of the pipeline (classes 17, 19, 22, and 24) and multiple systems (classes 20 and 21), the k-means classification of stellar spectra with continuum seems to separate stars according to their position on the color–color plot. The classes form a one-dimensional set in the diagram, with a bifurcation at g − r ≃ 0.5. The bifurcation separates dwarf stars (on top) from giant stars, a result further discussed below. We note, in passing, that multiple systems are well separated in this color–color plot and, therefore, it can be used to select them.

Zoom In Zoom Out Reset image size

Main-sequence stars have log (g) larger than 3.8 (with the surface gravity g in cm s⁻²), which is even larger (log (g) > 4) for stars with T_eff < 9000 K (e.g., Drilling & Landolt 2000). Figure 10 shows the two-dimensional distribution of log (g) versus T_eff, together with contours with the region containing 68% of the stars in the class. The gravities and effective temperatures of individual stars have been taken from the SSPP (parameters labeled ADOP), as we explain in Section 2. The plot does not include all the classes since many of them overlap and would clutter the figure. Only those classes relevant for our argumentation are included, in particular classes 0 and 3 have similar T_eff but are parts of the two different branches of the color sequence (see Figure 9). Note that class 0 gathers only main-sequence stars (log (g) > 4) whereas most class 3 targets are giants. Something similar occurs with the pairs of classes 1 and 5, and 8 and 11. Classes 0, 1, 4, and 8 contain only main-sequence stars (see classes 0 and 8 in Figure 10). Classes 14 and 18 contain only giant stars (see class 18 in Figure 10). Several classes do not have enough valid T_eff and log (g) to know their location in the log (g) versus T_eff plot, including the classes with faults plus classes 16 and 25. Class 25 is a minor class with few elements, but class 16 is not. The lack of effective temperatures and gravities for class 16 seems to be associated with the fact that it collects WDs, for which no proper physical data are provided by the SSPP (but see, e.g., Eisenstein et al. 2006; Kleinman 2010; Tremblay et al. 2011). We note that classes 20 and 21, multiple systems whose spectra combine hot and cold components (see Figures 4 and 8), appear in Figure 10 as main-sequence stars with T_eff between 5000 K and 6000 K. They are also metal rich systems according to the plot discussed in the next paragraph.

Zoom In Zoom Out Reset image size

Figure 11 shows the two-dimensional distribution of [Fe/H] versus T_eff, together with contours with the region containing 68% of the stars in the class. As the rest of physical parameters of stars, the metallicity [Fe/H] comes from the SSPP. The figure shows how the classes often contain both high- and low-metallicity stars. If the threshold between low and high metallicities is set at one-tenth of the solar value (i.e., [Fe/H] =−1), the classes that contain only high-metallicity stars are 0, 1, 4, 8, 14, and 18. Similarly, classes 12 and 15 include only low-metallicity stars. Some of these classes are included in Figure 11. Class 18 contains low-gravity, low-temperature high-metallicity stars—probably K giants. Class 15 contains low-gravity, high-temperature low-metallicity stars.

Zoom In Zoom Out Reset image size

The k-means classes do not exactly coincide with the classical MK types assigned to the stars by Lee et al. (2008b; see Section 2). Figure 12 presents the histogram of MK types corresponding to the k-means classes in Figures 10 and 11. As the histograms show, most classes can be ascribed to a single MK type or to a narrow range of them (e.g., classes 0, 8, and 9). However, the spread in MK types is sometimes large (e.g., class 18), becoming extreme in the bluest classes (e.g., class 15), which often group A-type stars (mainly on the horizontal branch) with WD.

Zoom In Zoom Out Reset image size

To recapitulate, the k-means classification of spectra with continuum seems to be basically a color classification. The stellar colors are driven mostly by the overall continuum shape, therefore, the k-means classes separate stars according to their continua.

4.2. Classes with Continuum Removed

As explained in the previous section, the k-means classification of stellar spectra with continuum is essentially a color classification. Since the colors are dictated mostly by the continuum, the classification is driven by the shape of the continuum. Dust extinction and errors in the spectro-photometric calibrations corrupt continua but not so much spectral lines, which retain the information on the stellar properties. In order to study the potential of k-means to identify and separate spectra according to subtle spectral-line differences, we repeated the classification using spectra without continuum. Explicitly, the spectra to be classified are the original spectra after removal of a running mean filter 193 pixels wide, which corresponds to 170 Å in the blue and 400 Å in the red. The width of the numerical filter was determined as a trade off to be broader than most spectral features, yet narrow enough to be representative of the local continua. Because SDSS spectra are sampled in log wavelength, our constant width in pixels represents a single Doppler broadening of the order of 17,400 km s⁻¹.

The procedure leading to the classification is similar to that used for the full spectra described in Section 4.1. The dispersion, coincidence, and number of major classes were used to select one among 100 independent initializations. The selection criteria try to make this classification as representative of the rest as possible. The selected class has coincidence = 75.7%, dispersion = 0.051, 13 mayor classes, and 1 minor class. Note that the coincidence is larger than that for the classification with continuum, and the dispersion and number of classes smaller. The number of stars in each class is shown in Figure 13. As we did for the classes resulting from classifying the spectra with continuum (Section 4.1), the new classes are also named class 0, class 1, and so on, with the number increasing as the elements in the class decrease. The average spectra of all the stars in each class are shown in Figure 14. We just show a small portion of the blue spectrum where individual spectral lines can be appreciated. (Two spectra spanning the full spectral range are shown for illustration, but then it is impossible to appreciate details of the lines.) Note that each template spectrum is the average of thousands of individual spectra, so all the small noise-looking wiggles are real spectral features. The full templates are shown as a stack-plot image in Figure 15 (cf. Figure 6). They have been ordered so that the sequence looks as smooth as possible. The Balmer lines, which are the only ones present in class 12, decrease in strength as one moves up in the image. The conspicuous molecular bands of TiO are present only in class 7. Figure 16 also shows the average spectra of the classes, but this average was computed using the original spectra with their continua intact. The comparison of these spectra with those corresponding to the classification including continuum (Figure 4) renders a few differences. First, the faulty classes with a fake emission peak in the blue (e.g., class 17 in Figure 4) have disappeared. This is a side effect of removing the continuum from the spectra, which in our implementation blacks out the 193 pixels in the extreme wavelengths, thus removing the problem. Second, there is a new class that shows spectra with emission lines (class 9), which most probably are not real but poorly corrected sky lines at the wavelengths of the Ca ii IR triplet (see, e.g., Lee et al. 2008b). Finally, the spectra corresponding to binary systems do not form a separate class, so that they have to show up as outliers of the classification (Section 5).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The classes are shown in the u − g versus g − r color plot in Figure 17. They overlap more than the classes inferred when the continuum is included; see Figure 9. There are several conclusions to be drawn from the comparison of these two figures. The continua influence the classification or, in other words, the classifications with and without continua do not fully agree. However, most classes can be viewed as mergers of classes with continuum. Even if the continuum is not included for classifying, the different classes have different colors—classes 0 and 9 represent an exception since they overlap in the color–color plot (see Figure 17). The color–color plot also shows two parallel sequences that split at g − r ∼ 0.2 (or at class 6). As it happens with the classification including continuum, the upper branch corresponds to main-sequence stars whereas the lower branch includes giants. This separation by stellar size is more clear in Figure 18, which shows the two-dimensional distribution of log (g) versus T_eff for the stars in a number of selected classes—the classes in the lower branch of Figure 17 include low-gravity stars in Figure 18 (see classes 6 and 2). Figure 19 shows the two-dimensional distribution of [Fe/H] versus T_eff for the full set of stars, together with contours with the region containing 68% of the stars in selected classes. Note how well separated are the classes in this plot, in contrast with the overlap present in the color–color plot (Figure 17). The behavior is opposite to that of the classes resulting from classifying spectra with continua, which are well separated in the color–color plot (Figure 9), but overlap in the [Fe/H]–T_eff diagram (Figure 11). Note also that classes 5 and 6 occupy the same region of the color–color plot and overlap in the log (g)–T_eff plot, but they have different metallicities. These are F stars that approximately split according to their membership to the thick disk and the halo (Allende Prieto et al. 2006); therefore, the classification provides a quick-look tool to separate disk and halo stars. Class 12 is dominated by DA WDs (see below and the class template in Figure 16), however, it shows up as extremely low metallicity in Figure 18. Since the SSPP does not deal with WDs, these must have been confused with A-type stars and analyzed as such, finding that they are best matched with no metals.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 20 shows the distribution of MK spectral types corresponding to the k-means classes. Note how each class tends to belong to a single spectral type, but not always. Moreover, the correspondence seems to be better than that for the classification including continuum (cf. Figure 12). Note how class 12 is basically formed by WDs, whereas classes 8, 10, and 11 are made of type A stars. The most numerous class 0 contains almost exclusively F9 stars, as it also happens with the classification with continuum (Figure 12). We think that the concentration of class 0 around a particular type is real, but the particular type is not, since most stars selected by SEGUE are G-type rather than F-type (see Section 2). There seems to be a problem with the MK typing based on ELODIE templates because, as expected, the Hammer MK types associated with class 0 are late G types. Figure 21 is equivalent to Figure 20 but showing Hammer types (Section 2). Class 0 corresponds to types between G6 and K2. Note, in passing, that the classes of hot stars have disappeared from the histograms since Hammer typing does not allocate classes to them.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table 1 gives a summary of the physical properties of the classes, namely, it contains mean values and standard deviations for colors, temperatures, gravities, and metallicities. (Class 13 has been excluded since it seems to be collecting faulty spectra.) Note that some classes present a fairly small range of physical parameters. For instance, if a star is assigned to class 0 then we know its temperature, gravity, and metallicity with standard deviations of 190 K, 0.25 dex, and 0.36 dex, respectively. These uncertainties are comparable to those associated with other approaches currently used to estimate effective temperature and gravity. This fact opens up the possibility of using k-means for a quick-look estimate of the main physical parameters of the stars at a minimum computational cost. Once the classes are known, assigning a new spectrum to one of them is virtually instantaneous—it is just a matter of computing the difference between the new spectrum and the class templates, and then selecting the class of least rms deviation.

Table 1. Properties of the Stellar Classes from Spectra without Continuum

Class	g − r	u − g	Teffa	log (g)b	[Fe/H]c
0	0.64 ± 0.08	1.39 ± 0.20	5370 ± 190	4.51 ± 0.25	−0.53 ± 0.36
1	0.53 ± 0.10	1.03 ± 0.17	5660 ± 290	4.13 ± 0.47	−0.79 ± 0.40
2	0.60 ± 0.13	0.96 ± 0.21	5450 ± 340	3.33 ± 0.75	−1.71 ± 0.53
3	0.87 ± 0.13	1.86 ± 0.29	4830 ± 230	4.61 ± 0.22	−0.52 ± 0.40
4	1.02 ± 0.25	1.70 ± 0.44	5260 ± 440	3.74 ± 0.74	−0.55 ± 0.50
5	0.36 ± 0.12	0.74 ± 0.13	6400 ± 300	3.98 ± 0.35	−0.79 ± 0.45
6	0.30 ± 0.20	0.64 ± 0.23	6500 ± 330	3.74 ± 0.47	−1.86 ± 0.61
7	1.31 ± 0.17	2.24 ± 0.33	4290 ± 150	4.39 ± 0.34	−0.55 ± 0.42
8	0.18 ± 0.14	0.64 ± 0.17	7250 ± 340	4.05 ± 0.37	−0.90 ± 0.62
9	0.69 ± 0.16	1.31 ± 0.35	5340 ± 330	4.24 ± 0.47	−0.89 ± 0.50
10	0.02 ± 0.14	0.59 ± 0.17	8020 ± 340	4.12 ± 0.40	−0.98 ± 0.70
11	−0.14 ± 0.08	0.49 ± 0.12	8700 ± 350	3.80 ± 0.47	−1.36 ± 0.66
12	−0.27 ± 0.13	0.35 ± 0.18	8890 ± 410	4.67 ± 0.17	−3.03 ± 0.66

Notes. ^aEffective temperature in K. ^bGravity g in cm s⁻². ^cMetallicity in logarithmic scale referred to the Sun.

Download table as:  ASCIITypeset image

Having a classification automatically provides outliers, i.e., uncommon objects which therefore do not belong to any of the classes. We can easily identify them since, in addition to assigning class memberships, our algorithm estimates the probability of belonging to the class (see Section 3). Outliers are therefore those objects whose probability of belonging to their class is below a threshold. We set the threshold to 0.01, which implies selecting as outliers the 1% spectra furthest from their clusters' centers. The actual threshold is both arbitrary and unimportant, since our purpose was figuring out the type of spectra that do not fit in the classification. The adopted threshold renders some 2200 spectra that were inspected individually.

We carried out the inspection for both classifications, the one including continuum and the one without continuum. In both cases, the vast majority of the outliers are noisy spectra or failures of the SDSS pipeline (e.g., gaps, unsuccessful removal of telluric lines, mismatches between the red and the blue spectrograph arms, and so on). These problematic spectra represent three-quarters of the outliers for the classification using continuum, and a bit less when continuum is removed. (This difference is to be expected since subtracting the continuum automatically cancels many of the calibration problems.) Here, we focus on the outliers of the classification with continuum, although they are qualitatively similar to those of the classification with the continuum subtracted. In this case we count 548 genuine outliers. They are illustrated in Figure 22 and described in the following list ordered from more to less common.

• 1.  
  Quasars (QSOs) at redshift between 2 and 4, so that Lyα appears in the visible spectral range (e.g., Figure 22(a)—we identified the observed lines in the QSO spectrum template by Francis et al. 1991). Most outliers are of this kind (some 320 or 60% of the sample). They represent only 0.3% of QSOs in the latest SDSS QSO catalog (Schneider et al. 2010), but they tend to appear in the redshifts where the SDSS identification algorithm has known problems (redshifts 2.9 and 3.2). A bad redshift assignation at these particular redshifts would explain the presence of a large number of QSOs contaminating our stellar sample.
• 2.  
  Broad absorption line (BAL) QSOs at the same high redshifts (Figure 22(b)). Those are believed to be active galactic nuclei with very rapid outflows (of a few times 10⁴ km s⁻¹) along the line of sight (Gibson et al. 2009). We get 33 of these objects, which represent 6.0% of the outliers and 9.3% of the QSO—a percentage that seems to be normal for BAL QSOs (e.g., Gibson et al. 2009).
• 3.  
  Composite spectra of blue and red stars combined (e.g., Figure 22(c), where Hα shows up in emission). They may be genuine binary systems with the two stars gravitationally bounded or just two or more stars that happen to be along our line of sight. We ignore why these stars appear as outliers rather than elements of existing classes (classes 20 or 21 in Figure 4), but it may be due to having an excess of blue upturn as compared to the template spectra.
• 4.  
  Flat spectra, showing absorption line feature characteristics of hot stars in the blue, and of cold stars in the red (e.g., Figure 22(d)). They may be composite spectra like in Figure 22(c), but with the luminosities of the stars fine-tuned so that the combination looks spectrally flat.
• 5.  
  Extreme spectra. They look-like the corresponding templates, but seem to be extreme cases (e.g., extreme colors or particularly deep absorption lines). Figure 22(e) shows a particularly cold star or sub-stellar object—the spectrum and the corresponding template are shown as solid and dotted lines, respectively. Figure 22(f) shows the spectrum of a star (the solid line) hotter than its template (the dotted line).
• 6.  
  Star-forming galaxies at intermediate redshifts (e.g., Figure 22(g)).
• 7.  
  QSOs at redshifts around one (e.g., Figure 22(h)).
• 8.  
  Strongly dust-reddened blue stars (e.g., Figure 22(p)).
• 9.  
  Carbon rich WDs with strong C₂ bands (e.g., Figure 22(i) and 22 j)—see the observed and synthetic spectra in Wegner & Yackovich (1984).
• 10.  
  Carbon stars (e.g., Figure 22(o)), where the photospheric opacity is dominated by C-bearing molecules. The carbon, dredged up to the photosphere, comes from the He burning shell characteristic of low-mass stars during their late stages of evolution (e.g., Aringer et al. 2009). Figure 22(o) should be compared with C-star spectra in, e.g., Loidl et al. (2001, Figure 4) and Aringer et al. (2009, Figure 3).
• 11.  
  Strange-looking spectra. They may be failures of the reduction pipeline, but they may be genuine abnormal objects as well. Figures 22(k)–(n) show a few of them, chosen only when they are not the sole representative of its class. They include spectra with strong emission lines (e.g., Figure 22(m)) or spectra with a single absorption line (e.g., Figure 22(n)).

Zoom In Zoom Out Reset image size

The traditional approach to classify stellar spectra has to be adapted to process the volume of data produced by large surveys underway (see Section 1). There is a need for new automated techniques of analysis. In this work, we explore the use of the algorithm k-means for the task, i.e., as a tool for the automated unsupervised classification of massive stellar spectrum catalogs. The algorithm has already proven its potential for fast processing other astronomical spectra (Section 1), and we expected it to be useful in this context as well.

For this exploratory application of k-means, we selected the data set of stellar spectra associated with the SEGUE and SEGUE 2 programs. Even though it is not a fair sample of the Milky Way stellar populations, it contains a rich variety of stellar types and so it is a good test bench for the classification algorithm. After discarding faulty cases, the reference data set consists of 173,390 stellar spectra from 3800 to 9200 Å sampled in 3849 wavelengths. Therefore, the problem for k-means is to find clusters among 173,390 vectors defined in a 3849 dimensional space. The full data set occupies 6.1 GB and is classified using a standard up-to-date workstation for about two hours (see Section 3.1).

We apply the classification to the original spectra and also to the spectra with the continuum removed. The latter data set contains only spectral lines, and it is less dependent on observational and instrumental problems like dust extinction, spectro-photometric miscalibrations, or failures in the reduction pipeline.

The classification of the spectra with continuum renders 16 major classes, with 99% of the objects, and 10 minor classes with the remaining 1% (Section 4.1). Roughly speaking, the stars are split according to their colors, with enough finesse to distinguish dwarf and giant stars (Figure 9). Figure 4 shows the template spectra representative of all the classes: there are classes for WDs (class 15), A-type stars (class 9), F-type stars (class 0), K-type stars (class 8), M-type stars (class 23), dust-reddened intrinsically blue stars (class 18), binary systems (class 21), and even classes with faulty spectra (classes 17 and 19). It must be stressed, however, that there is not a one-to-one correspondence between the classes we derived and the MK types. Often our classes mix-up several MK types, and vice versa. The classification is able to separate stars with similar temperatures but different surface gravities (compare classes 0 and 3 in Figure 10), but has difficulties separating stars with different metallicities (Figure 11).

The classification of spectra without continuum renders less classes (Section 4.2)—13 major classes and only 1 minor class that probably collects faults of the reduction pipeline (Figures 14 and 16). In this case, the color separation is not as sharp as it is for the classification with continuum included (cf. Figures 9 and 17). However, it is able to separate stars in classes with the same effective temperatures but different metallicities (Figure 19). The behavior is opposite to that of the classes resulting from classifying spectra with continua, which are well separated in the color–color plot but overlap in [Fe/H] versus T_eff.

Some classes include starts with a fairly small range of physical parameters, as assigned by the SSPP. The mean value and dispersion of the effective temperature, surface gravity, and metallicity of the classes without continuum are listed in Table 1. A small dispersion implies that our classification can be used to estimate the main physical parameters of the stars at a minimum computational cost. One only has to assign the problem spectrum to one of the existing classes, e.g., to the one of minimum residual. Then the properties of the class can be passed on to the new spectrum, thus providing its main physical properties. For example, if the problem spectrum happens to belong to class 0, then we know its temperature, gravity, and metallicity within a standard deviation of 190 K, 0.25 dex, and 0.36 dex, respectively. These uncertainties are probably upper limits since the estimate of the physical parameters by the SSPP has non-negligible internal errors that are included in the dispersions. Note that the uncertainties are comparable with those associated with other approaches currently used to estimate effective temperature and gravity, which are far more time consuming. Moreover, since we derive physical parameters from spectra without continuum, the estimates are fairly robust against dust reddening and other observational issues, which are often a serious problem when dealing with stars at low galactic latitudes.

The classification also provides a means of finding rare but scientifically interesting objects, e.g., unusually low-metallicity stars, odd spectral types, etc. By definition, rare objects must be outliers of any classification, otherwise they would be common and would have classes associated with them. Our rendering of k-means gives the goodness of the assignation, i.e., the probability that each star belongs to the class it has been assigned to. Therefore, the outliers of the classification are easy to pinpoint as those spectra whose probability of a correct assignation is low enough. The nature of the outliers thus selected was examined in Section 5—see Figure 22. Most outliers are faulty data or failures of the SDSS reduction pipeline. The remaining 25% is first formed by high-redshift QSOs. Since they are in the appropriate redshift range, we speculate that these QSOs may be those lost by a known problem in the SDSS QSO identification algorithm. There is a large number of outliers corresponding to composite spectra formed by either real or fake double or multiple stellar systems. The spectrum is that of a hot star in the blue and a cold star in the red. There are also reddened stellar spectra and galaxy spectra. Finally, there are odd spectral types whose nature we did not manage to figure out, and which we plan to observe in follow-up work.

One obvious use of the present classification is identifying spectra having instrumental problems or being produced by flaws of the reduction pipeline. We find classes containing faulty spectra when the problem is common, and then we find faulty spectra as outliers of the classification when the problem is unusual.

Stellar spectra are known to be highly compressible so that they can be characterized using only a few independent parameters (see Section 1). Then the fact that the classes present a regular behavior was somehow expected, and this fact is not the main outcome of our exercise. Instead, our exploratory work shows that k-means provides a viable tool for the systematic classification of large data sets of stellar spectra. Moreover, there is plenty of room for improving the procedure, i.e., for upgrades that have not been considered in the paper, but which may be of interest in future uses. One can focus the classification in a particular spectral range (or set of ranges) particularly sensitive to the physical parameter one wants to select (say, the metallicity if searching for classes of extremely metal-poor stars). Then the resulting classes would emphasize this particular aspect of the spectra. Obviously, using smaller spectral ranges for classification also speeds up the procedure. One can also resort to nested k-means classifications, where the spectra of a given class are separated into subclasses. This can be used for fine-tuning separation.

Finally, we want to indicate that the template spectra from the classifications with and without continuum are publicly available through the online journal and at ftp://stars:kmeans@ftp.iac.es.

Thanks are due to J. Casares, L. Girardi, and C. Ramos-Almeida for help with deciphering the nature of some of the outliers, and to I. Ferreras and B. Gustafsson for illuminating discussions. In addition, we thank the referee, C. Bailer-Jones, for his constructive criticisms that tempered the statements made in the paper. This work has been partly funded by the Spanish Ministry for Science, project AYA 2010-21887-C04-04. J.S.A. is member of the Consolider-Ingenio 2010 Program, grant MICINN CSD2006-00070: First Science with GTC. Funding for SDSS, SDSS-II, and SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, University of Cambridge, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.

Facility: Sloan (DR8, spectra) - Sloan Digital Sky Survey Telescope