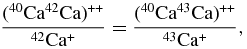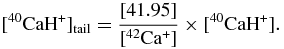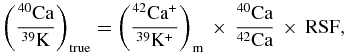ABSTRACT
The short-lived radionuclide 41Ca plays an important role in constraining the immediate astrophysical environment and the formation timescale of the nascent solar system due to its extremely short half-life (0.1 Myr). Nearly 20 years ago, the initial ratio of 41Ca/40Ca in the solar system was determined to be (1.41 ± 0.14) × 10−8, primarily based on two Ca–Al-rich Inclusions (CAIs) from the CV chondrite Efremovka. With an advanced analytical technique for isotopic measurements, we reanalyzed the potassium isotopic compositions of the two Efremovka CAIs and inferred the initial ratios of 41Ca/40Ca to be (2.6 ± 0.9) × 10−9 and (1.4 ± 0.6) × 10−9 (2σ), a factor of 7–10 lower than the previously inferred value. Considering possible thermal processing that led to lower 26Al/27Al ratios in the two CAIs, we propose that the true solar system initial value of 41Ca/40Ca should have been ∼4.2 × 10−9. Synchronicity could have existed between 26Al and 41Ca, indicating a uniform distribution of the two radionuclides at the time of CAI formation. The new initial 41Ca abundance is 4–16 times lower than the calculated value for steady-state galactic nucleosynthesis. Therefore, 41Ca could have originated as part of molecular cloud materials with a free decay time of 0.2–0.4 Myr. Alternative possibilities, such as a last-minute input from a stellar source and early solar system irradiation, could not be definitively ruled out. This underscores the need for more data from diverse CAIs to determine the true astrophysical origin of 41Ca.
1. INTRODUCTION
Studies of the initial abundance and distribution of the short-lived radionuclide 41Ca (decays to 41K with a t1/2 = 0.1 Myr; Jörg et al. 2012) in the early solar system provide important constraints on the origin of this radioactivity, which is crucial for understanding the astrophysical environment in which the Sun was born. The origin of 41Ca (and some other radioactivities with half-lives around a few Myr present in the early solar system) still remains a matter of debate. From theoretical viewpoints, 41Ca can be delivered into the solar nebula as a nucleosynthetic product of different stars (supernova (SN), asymptotic giant branch (AGB) stars, or Wolf–Rayet (WR) stars) and/or is produced by nuclear reactions induced by energetic charged particles bombarding ambient gas or dust near the proto-Sun (e.g., Meyer 2005; Lee et al. 1998; Gounelle et al. 2001, 2006; Arnould et al. 2006; Wasserburg et al. 2006). These contrasting origins would then have different implications for the processes and timescales of solar system formation (Dauphas & Chaussidon 2011). In a stellar origin hypothesis, the expected uniformity of 41Ca abundance in the solar nebula (as a result of hydrodynamic mixing, e.g., Boss 2007, 2011) would not only make it potentially useful for chronology, but also provides a stringent constraint on the time span between its nucleosynthesis and incorporation into the early solar system material. In contrast, in situ irradiation production could have resulted in variable 41Ca abundances throughout the nebula, rendering chronological applications invalid. It is however not possible to favor one source over the other unless a comprehensive understanding of the abundances of 41Ca and its relationship with other short-lived radioisotopes in the oldest solar system materials, namely Ca–Al-rich Inclusions (CAIs), is constructed.
In the past 20 years, there have only been limited data reported for 41Ca primarily due to analytically challenging mass spectrometry (see below). Earlier studies carried out on small-geometry Secondary Ion Mass Spectrometers (SIMS) have revealed large excesses of radiogenic 41K (≡ 41K*) in correlation with the 40Ca/39K ratios of the phases (primarily fassaite, a Ti-rich pyroxene) measured in CAIs from the CV3 chondrites Allende and Efremovka and a CM2 chondrite Murchison, indicating the existence of 41Ca in the early solar system at the level of 41Ca/40Ca ∼ 1.4 × 10−8, albeit with large analytical uncertainties (Srinivasan et al. 1996; Sahijpal et al. 2000). Such a discovery implies, if 41Ca was injected into the solar nebula from a dying star, a short timescale (<1 Myr) for its nucleosynthetic production, transit, and incorporation into CAIs (Srinivasan et al. 1996). This interpretation was strengthened by the later discovery of the correlated presence or absence between 26Al (t1/2 = 0.7 Myr) and 41Ca in both CV CAIs and CM hibonite (CaAl12O19) grains: samples characterized by the "canonical" 26Al/27Al ∼ 5 × 10−5 contained 41Ca/40Ca ∼ 1.4 × 10−8; in contrast, the 26Al-free inclusions were devoid of 41Ca (Sahilpal et al. 1998). Given that widespread 26Al/27Al = 5.2 × 10−5 in the early solar system during CAI formation is believed to have resulted from an injection of 26Al from a stellar source followed by hydrodynamic mixing in the nebula (e.g., Boss 2007, 2011), this correlation could then be understood as a consequence of co-injection and co-homogenization in the solar nebula after some CAIs have formed (Sahijpal & Goswami 1998).
It should, however, be noted that the assessment of true 41K* level in a mineral relies significantly on the accuracy of estimates and correction for all interferences at mass/charge (m/e) 41. For example, three different initial 41Ca/40Ca ratios, (8 ± 3) × 10−9, (1.2 ± 0.2) × 10−8, and (4.1 ± 2.0) × 10−9, inferred from the isotope analyses performed on small-geometry SIMS (the first two; see Hutcheon et al. 1984 and Sahijpal et al. 2000) and large-geometry SIMS (the last one; Ito et al. 2006), have been reported for the CAI EGG3. Although these controversial results have been attributed to isotope disturbances of potassium in that CAI by Sahijpal et al. (2000) and Ito et al. (2006), the robustness of corrections for all the peaks interfering with 41K could have also been a cause. The large systematic uncertainties derived from deconvolving the interferences from real 41K* and the limited amount of data available so far have not allowed for a quantitative evaluation of the level of 41Ca/40Ca in the solar nebula. To better quantify the true initial 41Ca abundance, the first step is to reexamine the potassium isotopic compositions with a new high mass-resolution, high transmission ion microprobe (SIMS) in the CAIs where fossil records of 41Ca have been previously demonstrated. Here we report the new isotopic results of the 41Ca–41K system in two CAIs from Efremovka, where evidence of in situ decay of 41Ca was revealed (Srinivasan et al. 1996), and discuss the implications for the origins of short-lived 41Ca and solar system formation.
2. EXPERIMENTAL
2.1. Samples
The samples studied here are the E44 and E65 CAIs from the CV chondrite Efremovka. They are of particular importance in potassium isotopic analyses because the prior existence of 41Ca/40Ca = 1.4 × 10−8 in the solar system was primarily inferred in them (Srinivasan et al. 1996). Other earlier studies on their petrology, mineral chemistry, and magnesium and boron isotopic compositions can be found in Goswami et al. (1994), Young et al. (2005), McKeegan et al. (2001), and Srinivasan & Chaussidon (2012). Recent high precision analyses of Mg isotopes revealed that E44 and E65 are characterized by 26Al/27Al ratios of (4.8 ± 0.3) × 10−5 and (4.46 ± 0.25) × 10−5 (Young et al. 2005; Srinivasan & Chaussidon 2012), respectively. The two inclusions have also been shown to preserve fossil records of 10Be (t1/2 = 1.3 Myr; Korschinek et al. 2010), with 10Be/9Be = (8.4 ± 1.9) × 10−4 and (7.0 ± 1.7) × 10−4 consistent with one another within analytical uncertainties (McKeegan et al. 2001; Srinivasan & Chaussidon 2012).
2.2. Mass Spectrometry
Measurements of potassium isotopes were made on the CAMECA 1280 HR2 ion microprobe at CRPG, Nancy. The major challenge in obtaining the true radiogenic component of 41K is to accurately quantify the magnitudes of all interferences at m/e = 41, including (40Ca42Ca)++ and scattered ions from 40Ca+ and 40CaH+ tails, and correct for them. Given that the initial 41Ca/40Ca ratio in the early solar system appears to be ≈10−8, only phases with 40Ca/39K exceeding 5 × 105 (K concentrations <200 ng g−1) could potentially provide large enough 41K excesses compared to the analytical errors. However, two problems come with such high 40Ca/39K ratios. First, low K count rates, especially at mass 41, limit the analytical precision. Second, intensities of Ca-related interferences at m/e = 41 become significant relative to that of 41K+, making accurate determinations of 41K/39K ratios very difficult. These challenges, in theory, could be eased by using a large-geometry SIMS, whose high throughput and high mass resolution (compared to those of smaller ones, e.g., CAMECA 3-7f) help improve analytical precision as well as separation between interferences and the peaks of interest.
The 1280HR2 was operated with a mass resolution (M/ΔM) of 8000, sufficient to separate 40CaH+ from 41K+, and other minor interferences from the peaks of interests (Figure 1). Since the major interference at mass 41, (40Ca42Ca)++, was not resolvable under any available mass resolution (M/ΔM = 34,000 is needed), we estimated its contribution indirectly by assuming that the following equality holds (see Hutcheon et al. 1984; Srinivasan et al. 1996):
(40Ca43Ca)++ can be found at m/e = 41.5. Due to its extremely low intensity (<1 counts s−1), the location of (40Ca43Ca)++ (41.4607 amu) was set by anchoring the magnetic field to the reference peak (40Ca27Al16O)++ (41.4695 amu). The high transmission of the instrument enabled the measurement of (40Ca43Ca)++ to determine (40Ca43Ca)++/43Ca+ for every spot analysis, as opposed to stand-alone characterizations of this ratio independent of K isotope analyses (see Srinivasan et al. 1996). We confirmed that (40Ca43Ca)++/43Ca+ is matrix dependent (Hutcheon et al. 1984; Srinivasan et al. 1996), and the values obtained here are identical within errors to those in Srinivasan et al. (1996). We used the measured (40Ca43Ca)++/43Ca+ ratio in each run to estimate the level of (40Ca42Ca)++ in that given spot and correct for it.
Figure 1. Mass spectrum obtained on a hibonite standard at m/e = 41 and 41.5 on the CAMECA 1280 HR2 ion microprobe at CRPG, Nancy, at a mass resolution = 8000. Extra counts on the low-mass side of (40Ca43Ca)++ are derived from the dynamic background.
Download figure:
Standard image High-resolution imageIn addition to (40Ca42Ca)++, we carefully evaluated the levels of scattered ions from the tails of 40Ca+ and 40CaH+ at m/e = 41. The former, which was not accounted for in Srinivasan et al. (1996), was found at ≈3 × 10−10 × 40Ca+ by measuring in steps of 0.2 amu between masses 40 and 41, whereas the latter was estimated by measuring the signal at mass 41.95 and applying the following relationship (assuming the peak shape of 42Ca+ on the low-mass side is the same as that of 40CaH+):
Under our analytical condition, the ratio of scattered ions at m/e = 41 to the intensity of 40CaH+ was found to be 3 × 10−6. Such a correction is relatively minor (<1% of the total counts) compared to that for (40Ca42Ca)++ due to full separation between 40CaH+ and 41K. The dynamic background of the counting system was measured for 60 s at the beginning of each analytical cycle, and the typical count rates range from 0.02 to 0.05 counts s−1. This dynamic background was preferred over static background of ∼0.005 counts s−1 measured overnight for 10 hr at 60 s interval because the latter may lead to under correction. The true 41K/39K ratio of a spot was then obtained after summing up counts over the entire analysis (e.g., Ogliore et al. 2011) and stripping off the interferences:
In our analytical protocol, a polished sample was sputtered with a 10 nA 16O− primary beam, and secondary ions were collected by the axial electron multiplier (EM) in a peak-jumping mode, with the mass sequence of 38.7, 39K+, 41K+, 40CaH+, (40Ca43Ca)++, (40Ca27Al16O)++, 42Ca+, and 43Ca+. 40Ca was not measured to avoid additional uncertainties derived from the cross calibration between a Faraday cup and the axial EM. Before each analysis, ∼25 minute presputtering was applied to the sample surface to minimize the contaminations. The field aperture width was set at 2500 μm to block out scattered K ions from the vicinity of the analysis spot. An energy window of 50 eV was used. To correct for the peak and magnetic field drifts during a long analysis, both mass calibration and surface charging compensation were performed every five cycles. The count time on 41K+ and (40Ca43Ca)++ was set at 60 s to achieve sufficient counting statistics. Each measurement consisted of 25–50 cycles and required ∼2–4 hr of analysis time. Two terrestrial calcite standards with high 40Ca/39K ratios (>106, see Figure 2) were analyzed to ensure that the mass spectrometry and the interference correction scheme were properly performed. Although 40K was not measured, normal 41K/39K ratios within errors (0.072; Garner et al. 1975) obtained in all standard analyses indicated that the instrumental mass fractionation and the matrix effect on K isotope compositions were insignificant and would not affect the determination of 41K* in extraterrestrial samples.
Figure 2. Potassium isotopic compositions of the two terrestrial calcite standards. The 41K/39K ratios obtained are consistent with the terrestrial ratio (dashed line). Errors are 2σ.
Download figure:
Standard image High-resolution imageThe relative sensitivity factor (RSF) of Ca to K was determined to be 2.53 ± 0.01 (2σ) on a NIST 614 glass with known Ca and K concentrations (CaO = 12 wt% and K = 30 μg g−1; NBS Tech Report 1982). Given that Ca isotopes exhibited very limited instrumental mass fractionation in the NBS 614 glass (<2 amu−1), we calculated the true 40Ca/39K ratio of a measured phase as follows:
where 40Ca/42Ca = 151.03 (Niederer & Papanastassiou 1984).
3. RESULTS
The potassium isotopic compositions of E44 and E65 are tabulated in Table 1 and plotted in Figure 3. Only fassaite and melilite yielded high enough 40Ca/39K (>5 × 105) for determination of 41K*, with 39K+ count rates ranging from 15 to 1000 counts s−1. The (40Ca42Ca)++ interference comprises 5%–87% of the total measured signal at mass 41, depending on the 40Ca/39K ratio of the phase measured (Figure 4). In E44, an error-weighted-least-squares regression through all the data points yields (41Ca/40Ca)0 = (2.6 ± 0.9) × 10−9 (2σ, χ2 = 2.0), and the intercept (41K/39K)0 = 0.0721 ± 0.0004 is consistent with the terrestrial ratio. Similarly, low (41Ca/40Ca)0 = (1.4 ± 0.6) × 10−9 and normal (41K/39K)0 = 0.0725 ± 0.0002 (2σ) were found in the E65 CAI, although the scatter in the fitting appears to be larger (χ2 = 3.6) than that of E44. The new values are about a factor of 7–10 lower than the previously claimed (1.41 ± 0.14) × 10−8 by Srinivasan et al. (1996), but overlap 41Ca/40Ca = (4.1 ± 2.0) × 10−9 in EGG3 pyroxene determined by Ito et al. (2006).
Figure 3. Isochron diagrams for E44 and E65 CAIs. δ41K is defined as ((41K/39K)/(0.072) − 1) × 1000. Errors are 2σ.
Download figure:
Standard image High-resolution imageFigure 4. Fractions of different components that comprise the total signal at mass 41 in CAIs. The proportions of scattered ions from 40Ca+ and 40CaH+ are too small to be shown (<1%).
Download figure:
Standard image High-resolution imageTable 1. Potassium Isotopic Compositions of E44 and E65 CAIs
| Sample | 40Ca/39K (±2σ) | 41K/39K (±2σ) |
|---|---|---|
| E44 px1 | (5.38 ± 0.13) × 105 | 0.07442 ± 0.00154 |
| E44 px2 | (1.82 ± 0.11) × 106 | 0.07644 ± 0.00656 |
| E44 px3 | (7.24 ± 0.28) × 105 | 0.07162 ± 0.00269 |
| E44 px4 | (8.27 ± 0.21) × 105 | 0.07612 ± 0.00198 |
| E44 px5 | (8.37 ± 0.63) × 106 | 0.08722 ± 0.01766 |
| E44 px6 | (8.78 ± 0.38) × 105 | 0.07681 ± 0.00344 |
| E44 px7 | (3.67 ± 0.18) × 106 | 0.08283 ± 0.00744 |
| E44 px8 | (4.28 ± 0.20) × 106 | 0.08184 ± 0.00768 |
| E44 px9 | (7.37 ± 0.21) × 105 | 0.07468 ± 0.00214 |
| E44 px10 | (6.63 ± 0.17) × 105 | 0.07112 ± 0.00176 |
| E44 px11 | (6.13 ± 0.13) × 105 | 0.07308 ± 0.00142 |
| E44 px12 | (2.04 ± 0.61) × 106 | 0.07943 ± 0.00338 |
| E44 px13 | (1.74 ± 0.02) × 105 | 0.07259 ± 0.00054 |
| E65 px1 | (3.28 ± 0.05) × 105 | 0.07405 ± 0.00084 |
| E65 px2 | (1.08 ± 0.01) × 105 | 0.07259 ± 0.00052 |
| E65 px3 | (8.15 ± 0.26) × 105 | 0.07577 ± 0.00232 |
| E65 px4 | (3.93 ± 0.07) × 105 | 0.07296 ± 0.00102 |
| E65 px5 | (1.38 ± 0.22) × 107 | 0.10169 ± 0.04468 |
| E65 px6 | (1.38 ± 0.01) × 105 | 0.07218 ± 0.00048 |
| E65 px7 | (7.38 ± 0.06) × 104 | 0.07198 ± 0.00332 |
| E65 px8 | (1.45 ± 0.05) × 106 | 0.07394 ± 0.00332 |
| E65 px9 | (7.20 ± 0.18) × 105 | 0.07196 ± 0.00184 |
| E65 px10 | (6.27 ± 0.14) × 105 | 0.07359 ± 0.00148 |
| E65 mel1 | (2.04 ± 0.09) × 106 | 0.08046 ± 0.00394 |
| E65 mel2 | (5.43 ± 0.11) × 105 | 0.07552 ± 0.00114 |
| E65 mel3 | (1.67 ± 0.07) × 106 | 0.07756 ± 0.00344 |
| E65 mel4 | (9.70 ± 0.03) × 105 | 0.07205 ± 0.00222 |
| E65 mel5 | (1.90 ± 0.07) × 106 | 0.07164 ± 0.00309 |
| E65 mel6 | (7.46 ± 0.17) × 105 | 0.07242 ± 0.00138 |
| E65 mel7 | (2.38 ± 0.08) × 106 | 0.07396 ± 0.00331 |
| E65 mel8 | (5.57 ± 0.14) × 105 | 0.07435 ± 0.00144 |
| E65 mel9 | (7.98 ± 0.49) × 106 | 0.08432 ± 0.01008 |
| E65 mel10 | (1.36 ± 0.06) × 106 | 0.07078 ± 0.00262 |
Notes. The error of true 41K/39K was calculated by propagating the counting errors of stripped components ((40Ca42Ca)++, 40CaH+tail, and 40Ca+tail) into those of potassium isotopes. From counting statistics, (40Ca42Ca)++ contributes roughly <2% to the final error of 41K/39K, whereas the contributions from 40CaH+tail and 40Ca+tail are negligible because the two components comprise <1% of the total signals at mass 41 (see Figure 4).
Download table as: ASCIITypeset image
4. DISCUSSION
4.1. A New Estimate for Initial 41Ca/40Ca in the Early Solar System
The results obtained in this study are much lower than the previous value of Srinivasan et al. (1996), probably because the new SIMS enabled better separation between interferences and peaks of interest and more accurate corrections for the scattered ions at m/e = 41. However, it should be noted that the two CAIs could have been thermally processed after their formation, as was implied by their lower-than-canonical 26Al/27Al ratios. Given that K self-diffusivity is only marginally slower than that of Mg in melilite (e.g., 6.74 × 10−19 and 9.43 × 10−19 m2 s−1 at 1200 °C, respectively; Ito & Ganguly 2004; the diffusion coefficient of K in fassaite is not available), the extent to which the K isotopes were disturbed should be similar to (or slightly less than) the Mg isotopes. This suggests that the 41Ca/40Ca ratios inferred from our measurements should not represent the true solar system initial. Applying the resetting times of ∼80,000 years and ∼155,000 years to E44 and E65, respectively, as were calculated by scaling their 26Al/27Al ratios back to 5.2 × 10−5, we obtain converging values of 41Ca/40Ca = 4.55+2.60− 1.57 × 10−9 and 4.10+2.04− 1.30 × 10−9. Such 41Ca/40Ca ratios are perfectly consistent with the inferred 41Ca/40Ca = (4.1 ± 2.0) × 10−9 by Ito et al. (2006) in the EGG3 CAI that is also characterized by the canonical 26Al/27Al of (5.29 ± 0.39) × 10−5 (Wasserburg et al. 2011). This surprisingly good agreement between CAIs from two different meteorites suggests synchronicity between 41Ca and 26Al, albeit based on only three CAIs. As 26Al is believed to have been homogeneously distributed at 26Al/27Al = 5.2 × 10−5 in the solar nebula during the epoch of CAI formation (Jacobsen et al. 2008; Villeneuve et al. 2009), this apparent synchronicity would not only imply a uniformity of 41Ca/40Ca = (4.1–4.5) × 10−9 at the same time, but render 41Ca chronology legitimate. Considering the error associated with each value, we propose that 41Ca/40Ca ∼ 4.2 × 10−9 should be considered the best estimated initial ratio in the early solar system.
4.2. Possible Origins for 41Ca
The new initial 41Ca/40Ca ratio has important implications for the origin of this radionuclide and the timescale of solar system formation. Earlier explanations for 41Ca/40Ca = 1.4 × 10−8 involved a last-minute addition to the solar nebula, either by an injection from a stellar source or by in situ early solar system irradiation (e.g., Huss et al. 2009; Gounelle et al. 2001). This is because the expected "average" 41Ca/40Ca value in the interstellar medium (ISM) 4.5 billion years ago is only ∼(2–8) × 10−8, as can be calculated from Galactic Chemical Evolution (GCE; e.g., Wasserburg et al. 2006; Huss et al. 2009). Given the million-year (or longer) timescale for the formation of a molecular cloud and for a fragment of that cloud to collapse and form the Sun (Hartmann et al. 2001; Glover & Mac Low 2007), 41Ca directly inherited from the average ISM would have almost decayed away by the time of CAI formation. Even if 41Ca/40Ca = (2–8) × 10−8 happened to characterize the molecular cloud fragment from which the Sun was formed (which is possible since local 41Ca abundances in different parts of the ISM could be significantly different from the average value), the time span between the collapse of that fragment and the solar system formation would still make 41Ca/40Ca lower than 1.4 × 10−8 when CAIs formed.
Our revised initial 41Ca/40Ca ratio of 4.2 × 10−9 for the early solar system falls below the GCE prediction by about a factor of 4–16, albeit there are large uncertainties associated with such calculations. Although it is impossible to completely rule out a last-minute input of 41Ca from a dying star or protosolar irradiation, the need is certainly eased. It should also be pointed out that 41Ca produced by in situ neutron capture on 40Ca in the Efremovka parent body due to recent exposure to Galactic cosmic rays (GCRs) is still at least 10-fold lower than the observed 41Ca abundance (Srinivasan et al. 1996).
4.2.1. A Stellar Origin
Many studies have proposed that 26Al and 41Ca (along with some other short-lived radioisotopes besides 10Be) could have been derived from a stellar source (SN, AGB star, or WR star) present shortly before the time of solar system formation (for a review, see Huss et al. 2009). The main arguments in support of such an origin largely come from the inferred presence of 60Fe (t1/2 = 2.6 Myr; Rugel et al. 2009), a radionuclide that requires exclusively a stellar origin, in the early solar system. By fine tuning the free decay time (ΔT) and dilution factor, one can arrive at a self-consistent solution for 26Al, 41Ca, and 60Fe to match their initial abundances in the early solar system5 (e.g., Huss et al. 2009). With the new 41Ca/40Ca ratio ∼3 times lower than initially thought, a ∼0.15 Myr increase in ΔT is required. This time increase would not change the abundances of 26Al and 60Fe because of their longer half-lives. Therefore, 41Ca could in theory be brought into the nascent solar system along with 26Al and 60Fe. The synchronicity as well as the correlated presence and absence between 26Al and 41Ca observed here and in earlier studies (e.g., Sahijpal & Goswami 1998) could be understood in this context. However, very recent work on 60Fe has shown that the initial 60Fe/56Fe ratio could have been more than an order of magnitude lower than previously estimated (∼10−8; e.g., Tang & Dauphas 2012). Although one could still potentially obtain a self-consistent solution to explain the new abundances of 41Ca and 60Fe by fine-tuning different parameters of an injection model (e.g., ΔT, dilution factor, nucleosynthetic yields, mass cut, etc.), whether the new model parameters are physical will need to be scrutinized. Considering the new 60Fe results with our new 41Ca/40Ca initial ratio, it calls into question the need for a last-minute input from a dying star to explain the presence of 41Ca.
4.2.2. Early Solar System Irradiation
Evidence for intense irradiation occurring at the earliest stage of the solar system derives from the high but variable abundances of 10Be in CAIs, with 10Be/9Be ranging from 3 × 10−4 to ∼10−2, which were interpreted as a consequence of proton fluence variations (McKeegan et al. 2000; Chaussidon et al. 2006; Liu et al. 2010; Gounelle et al. 2012). With a favorable target chemistry (i.e., enriched in refractory elements, such as a CAI-like composition), irradiation processes involving nuclear reactions with energetic protons and alpha particles can be conducive to producing 10Be and 41Ca, but not 26Al. It should be pointed out that the abundances of 10Be and 41Ca can still be inferred by means of isochrons in this scenario because of two reasons. First, the daughter elements of 10Be and 41Ca, B and K, respectively, are too volatile to condense out of the nebula gas at the CAI-forming temperatures (∼1400 K or above); therefore, the initial Be/B and Ca/K ratios of a CAI should be infinity. Any B and K seen in CAI minerals must have been due to late addition, either in the meteorite parent bodies or in the cold regions of solar nebula. Depending on the degree to which different mineral phases were contaminated, which resulted in variations in elemental ratios, an isochron can certainly be formed to infer the abundance of 10Be or 41Ca. Second, some CAIs show isotopic and petrological evidence of remelting and recrystallization (e.g., MacPherson et al. 2012). These thermal processes can redistribute 10Be and 41Ca inside a CAI and make their initial abundances inferable through an isochron.
The two CAIs studied here are characterized by essentially the same 10Be/9Be ∼ 8 × 10−4 (Srinivasan & Chaussidon 2012; McKeegan et al. 2001; unfortunately no 10Be/9Be data exist for EGG3). This indicates that, assuming similar Be contents in E44 and E65, they have suffered similar degrees of proton spallation (i.e., fluence), and therefore should have similar amounts of spallogenic 41Ca produced within them. That the initial 41Ca/40Ca ratios in E44 and E65 are consistent with one another can be easily understood in this context. However, it has been shown that the proton fluence that yields 10Be/9Be ∼ 9 × 10−4 is capable of producing collateral 41Ca/40Ca ≈ 2 × 10−8 in a target with CAI chemistry, ∼4 times higher than our preferred initial ratio (e.g., Lee et al. 1998). It is difficult to reconcile the overproduction of 41Ca by irradiation unless one attributes it to the uncertainties associated with the calculations (e.g., uncertainties of cross section measurements, projectile compositions, and energy spectrum). Moreover, there are two other problems that an irradiation origin hypothesis is faced with. First, under the assumption of 41Ca being produced by irradiation of solids, a variation in 41Ca/40Ca among different CAIs, as is the case for 10Be, is expected. This would mean that in CAIs with 10Be/9Be different from 9 × 10−4, 26Al and 41Ca would show different synchronicity from what we observed here. More coordinated high-precision measurements for 41Ca and 10Be are needed to settle this issue. The other problem is the existence of 10Be in the samples devoid of 26Al and 41Ca, for example, platy hibonite crystals from CM chondrites (e.g., Liu et al. 2009, 2010). It has been argued that 26Al, 41Ca-free platy hibonite crystals could not have formed late, but instead are older than normal CAIs, due to the preservation of large anomalies (up to ∼40%) in neutron-rich isotopes (48Ca and 50Ti; e.g., Sahijpal & Goswami 1998; Liu et al. 2009). The decoupling between 41Ca and 10Be in these solids requires a certain irradiation condition that was only conducive to the production of 10Be but not of 41Ca. However, such a condition still remains unknown to us. Trapping of GCR 10Be by the molecular cloud core could potentially be a solution for the decoupling between 10Be and 41Ca (Desch et al. 2004), but this model still faces challenges in explaining the observed variations in 10Be/9Be ratios in CAIs and platy hibonite crystals (Liu et al. 2010).
4.2.3. Inheritance from the Molecular Cloud
The third possible origin for 41Ca in the early solar system involves an inheritance from the parent molecular cloud. The calculated average 41Ca/40Ca in the ISM is higher than our inferred solar system initial ratio. If the parent molecular cloud of the solar system was characterized by the ISM 41Ca/40Ca ratio, the abundance difference would allow for the possibility that 41Ca was inherited from the molecular cloud and incorporated into CAIs after a free decay time of 0.2–0.4 Myr. Such a timescale is broadly consistent with the general free-fall timescale of a fragment of a molecular cloud to form a star, which is on the order of 105–106 years depending on the density of the cloud fragment (e.g., Heitsch & Hartmann 2008; Banerji et al. 2009). A homogeneous distribution of 41Ca in the solar nebula and the concordant decay between 26Al and 41Ca would be natural consequences in this molecular cloud origin hypothesis. However, one should note that if 41Ca had come in as part of molecular cloud material, it would have to predate any refractory materials that formed in the solar nebula. The lack of 41Ca in platy hibonite crystals would certainly not fit into this picture, unless some later processes reset the potassium isotopes after41Ca had finished decaying in these crystals.
5. CONCLUSION
The reanalysis of the potassium isotopic compositions of E44 and E65 CAIs yielded inferred 41Ca/40Ca ratios of (2.6 ± 0.9) × 10−9 and (1.4 ± 0.6) × 10−9 (2σ), respectively, a factor of 7–10 lower than previously determined by Srinivasan et al. (1996). By scaling the 26Al/27Al of the two CAIs back to 5.2 × 10−5, we obtain an initial 41Ca/40Ca for the two CAIs merging around 4.2 × 10−9. We consider this the best representative initial abundance of 41Ca in the solar system. The synchronous decay between 26Al and 41Ca implies that the two radionuclides were homogeneously distributed in the solar nebula at least in the formation regions of refractory minerals and therefore they both could be used as chronometers. However, the low abundance of 41Ca makes an understanding of its astrophysical origins more difficult than it used to be. More measurements for 41Ca/40Ca in CAIs are certainly needed to shed light on which source contributed the most to the 41Ca inventory in the solar nebula.
We thank Matthieu Gounelle for invaluable comments and the referee for a critical review, which greatly improve the presentation of this paper. This work was supported by grants from National Science Council (Taiwan, ROC) NSC 101-2116-M-001-014 (M.-C. Liu), from European Research Council (ERC grant FP7/20072013 Grant Agreement No. [226846] Cosmochemical exploration of the first two Million Years of the Solar System–CEMYSS), -ANR-08-BLAN-0260-CSD6 (M. Chaussidon), and from NASA Cosmochemistry (K. D. McKeegan), for which we are appreciative. This is CRPG publication number 2207.
Footnotes
- 5
26Al/27Al = 5 × 10−5, 41Ca/40Ca = 1.5 × 10−8, and 60Fe/56Fe ∼ 7 × 10−7 were usually used in such studies.
- Arnould M., Goriely S. and Meynet G. 2006 A&A 453 653
- Banerji M., Viti S., Williams D. A. and Rawlings J. M. C. 2009 ApJ 692 283
- Boss A. P. 2007 ApJ 660 1707
- Boss A. P. 2011 ApJ 739 61
- Chaussidon M., Robert F. and McKeegan K. D. 2006 Geochim. Cosmochim. Acta 70 224
- Dauphas N. and Chaussidon M. 2011 Annu. Rev. Earth Planet. Sci. 39 351
- Desch S. J., Connolly H. C. Jr. and Srinivasan G. 2004 ApJ 602 528
- Garner E. L., Murphy T. J., Gramlich J. W., Paulsen P. J. and Barnes I. L. 1975 J. Res. Natl. Bur. Stand. 79A 713
- Glover S. C. O. and Mac Low M.-M. 2007 ApJ 659 1317
- Goswami J. N., Srinivasan G. and Ulyanov A. A. 1994 Geochim. Cosmochim. Acta 58 431
- Gounelle M., Chaussidon M. and Rollion-Bard C. 2012 ApJ in press
- Gounelle M., Shu F. H., Shang H. et al. 2001 ApJ 548 1051
- Gounelle M., Shu F. H., Shang H. et al. 2006 ApJ 640 1163
- Hartmann L., Ballesteros-Paredes J. and Bergin E. A. 2001 ApJ 562 852
- Heitsch F. and Hartmann L. 2008 ApJ 689 290
- Huss G. R., Meyer B. S., Srinivasan G., Goswami J. N. and Sahijpal S. 2009 Geochim. Cosmochim. Acta 73 4922
- Hutcheon I. D., Armstrong J. T. and Wasserburg G. J. 1984 Lunar Planet. Sci. Conf. 15 387
- Ito M. and Ganguly J. 2004 Meteorit. Planet. Sci. 39 1911
- Ito M., Nagasawa H. and Yurimoto H. 2006 Meteorit. Planet. Sci. 41 1871
- Jacobsen B., Yin Q.-z., Moynier F., Amelin Y. et al. 2008 Earth Planet. Sci. Lett. 272 353
- Jörg G., Amelin Y., Kossert K. and Lierse v. Gostomski C. 2012 Geochim. Cosmochim. Acta 88 51
- Korschinek G., Bergmaier A., Faestermann T. et al. 2010 Nucl. Instrum. Methods Phys. Res. B 268 187
- Lee T., Shu F. H., Shang H., Glassgold A. E. and Rehm K. E. 1998 ApJ 506 898
- Liu M.-C., McKeegan K. D., Goswami J. N. et al. 2009 Geochim. Cosmochim. Acta 73 5051
- Liu M.-C., Nittler L. R., Alexander C. M. O'D. and Lee T. 2010 ApJ 719 L99
- MacPherson G. J., Kita N. T., Ushikubo T., Bullock E. S. and Davis A. M. 2012 Earth Planet. Sci. Lett. 331 43
- McKeegan K. D., Chaussidon M., Krot A. N. et al. 2001 Lunar Planet. Sci. Conf. 32 2175
- McKeegan K. D., Chaussidon M. and Robert F. 2000 Science 289 1334
- Meyer B. S. 2005 ASP Conf. Ser. 341, Chondrites and Protoplanetary Disk ed A. N. Krot, E. R. Scott and B. Reipurth (San Francisco, CA: ASP) 515
- National Bureau of Standards 1982 National Bureau of Standards Certificate of Analysis—Standard Reference Materials: 614 and 615 Wafers
- Niederer F. R. and Papanastassiou D. A. 1984 Geochim. Cosmochim. Acta 48 1279
- Ogliore R. C., Huss G. R. and Nagashima K. 2011 Nucl. Instrum. Methods Phys. Res. B 269 1910
- Rugel G., Faestermann T., Knie K. et al. 2009 Phys. Rev. Lett. 103 072502
- Sahijpal S. and Goswami J. N. 1998 ApJ 509 137
- Sahijpal S., Goswami J. N. and Davis A. M. 2000 Geochim. Cosmochim. Acta 64 1989
- Sahijpal S., Goswami J. N., Davis A. M., Lewis R. S. and Grossman L. 1998 Nature 391 559
- Srinivasan G., Sahijpal S., Ulyanov A. A. and Goswami J. N. 1996 Geochim. Cosmochim. Acta 60 1823
- Srinivasan G. and Chaussidon M. 2012 Earth Planet. Sci. Lett. in press
- Tang H. and Dauphas N. 2012 Lunar Planet. Sci. Conf. 43 1703
- Villeneuve J., Chaussidon M. and Libourel G. 2009 Science 325 985
- Wasserburg G. J., Busso M., Gallino R. and Nollett K. M. 2006 Nucl. Phys. A 777 5
- Wasserburg G. J., Wimpenny J. and Yin Q.-z. 2011 Workshop on Formation of the First Solids in the Solar System 9038
- Young E. D., Simon J. I., Galy A. et al. 2005 Science 308 227