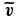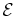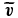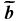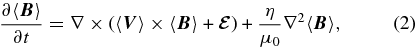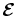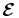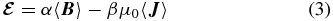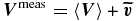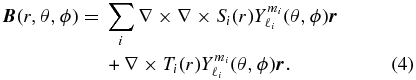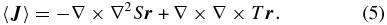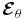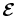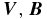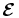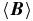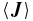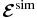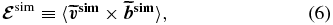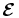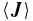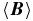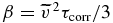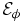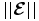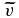DIRECT OBSERVATION OF THE TURBULENT emf AND TRANSPORT OF MAGNETIC FIELD IN A LIQUID SODIUM EXPERIMENT

Modeling astrophysical processes like stellar convection and accretion disk turbulence is accomplished only by assuming diffusivities for momentum, temperature, and magnetic fields far in excess of microphysical values. This assumption is one of the main challenges in the description of high Reynolds number flows and is a fundamental requirement for numerical modeling due to the many decades of separation between large-scale flows and dissipation scales. Molecular diffusivity, however, is irrelevant in these large systems compared with the effective mixing driven by turbulence in explaining the transport of momentum in accretion disks (Ji et al. 2006) and the transport of magnetic fields in the Earth and the Sun (Miesch & Toomre 2009; Glatzmaier & Roberts 1995).

Much effort at modeling turbulent transport has concerned the transport of scalar fields (e.g., temperature, concentration). Mixing length models provide a basic formulation of the problem (e.g., Böhm-Vitense 1958; Germano et al. 1991; Pope 2000). The transport of vector fields, like the magnetic fields that can dominate dynamics in astrophysical objects, is much more complicated. For instance, the topological properties of the flow are often essential for the description of elementary processes. Even in simple systems it is unclear whether the turbulent transport is adequately captured by parameterized treatments, e.g., if the transport is simply an enhanced diffusion or a combination of two or more underlying processes. Measurements of the turbulent electromotive force (emf) in low-beta plasma regimes (Ji & Prager 2002) and direct numerical simulations have studied the transport of magnetic fields and suggest that simple transport models might actually apply (Brandenburg & Subramanian 2005a), but, until now, only partial aspects have been confirmed experimentally (Reighard & Brown 2001; Stepanov et al. 2006; Spence et al. 2007; Frick et al. 2010).

Here we report the direct measurement of the three-dimensional (3D) turbulent electromotive force in isotropic turbulence where hydrodynamic instabilities drive the fluctuations and the magnetic stress is weak. Our essential finding is that the turbulent motions enhance the magnetic diffusivity: they generate an emf in opposition to the local current density. The measured emf is consistent with the calculated resistivity from mean-field theory.

Our present understanding of turbulence is still fragmentary. In particular the turbulent transport of vector quantities like momentum or magnetic fields is an area of active study. Turbulence is the natural state of all fluid or plasma systems that are driven sufficiently strongly. Turbulent flow patterns and dynamics are complex, and one of the key features of turbulent flows is that they lead to enhanced mixing. In hydrodynamic (non-magnetic) turbulence, mixing of momentum is the dominant process. Momentum is transported by nonlinear velocity interactions which are described by the Reynolds stress tensor ($\tau \equiv -\langle \widetilde{v}_i \widetilde{v}_j\rangle$, i.e., the correlation in the fluctuating velocity components). Measurements of τ have been essential in the evaluation of hydrodynamic turbulent transport models (Speziale 1991)—for instance, τ has been measured directly in model flows (Tao et al. 2002), in coastal ocean regions especially in the presence of surface waves (Rosman et al. 2008), and also has been measured in magnetically confined fusion plasmas (Hidalgo et al. 2000).

In magnetohydrodynamic (MHD) flows, the transport of magnetic flux is governed by the turbulent electromotive force (emf). Small-scale turbulent fluctuations in the velocity $\boldsymbol{\widetilde{v}}$ induce magnetic field fluctuations $\boldsymbol{\widetilde{b}}$. They coherently interact to produce, on average, an emf ${\cal E}$,

$$\begin{equation} \boldsymbol{\cal E} \equiv \langle\boldsymbol{\widetilde{v}}\times \boldsymbol{\widetilde{b}}\rangle. \end{equation} \tag{ 1 }$$

It is this turbulent emf that we study in our experiment by measuring $\boldsymbol{\widetilde{v}}$ and $\boldsymbol{\widetilde{b}}$ directly. $\boldsymbol{\cal E}$ affects the large-scale fields in the induction equation

$$\begin{equation} \frac{\partial \langle \boldsymbol{B}\rangle}{\partial t} = \nabla \times \left(\langle \boldsymbol{V}\rangle \times \langle \boldsymbol{B}\rangle + \boldsymbol{\cal E} \right) + \frac{\eta }{\mu _0} \nabla ^2 \langle \boldsymbol{B}\rangle, \end{equation} \tag{ 2 }$$

where 〈 · 〉 denote either a time average or a spatial average, and $\langle \boldsymbol{V}\rangle, \langle \boldsymbol{B}\rangle$ are the mean components of the flow and magnetic field, $\boldsymbol{\widetilde{v}}, \boldsymbol{\widetilde{b}}$ represent the fluctuating parts of flow and field, η is the resistivity, and μ₀ the vacuum permeability. In analogy with the turbulent eddy viscosity models developed for simple hydrodynamic turbulence, the so-called mean-field theory of MHD turbulence (Blackman & Field 2002; Brandenburg & Subramanian 2005b; Rädler & Stepanov 2006) has proposed closure models in which $\boldsymbol{\cal {E}}$ is related to the large-scale magnetic field and its derivative. For isotropic, homogeneous, helical turbulence, $\boldsymbol{\cal E}$ is expressed as

$$\begin{equation} \boldsymbol{\cal E} = \alpha \langle \boldsymbol{B}\rangle - \beta \mu _0 \langle \boldsymbol{J}\rangle\, \end{equation} \tag{ 3 }$$

with α, β transport coefficients related to the statistical properties of the turbulent flow. This simple parameterization leads to very mathematically efficient models of astrophysical dynamos (Ruzmaikin et al. 1989). The α contribution is often attributed to the stretching and twisting of magnetic fields lines (Pétrélis et al. 2003). The β contribution corresponds to an enhanced magnetic diffusion, analogous to the eddy viscosity in hydrodynamic turbulence. In the idealized framework of homogeneous and isotropic fluctuations, β is a scalar quantity which can be expressed as $\beta \approx \widetilde{v}^2 \tau _\mathrm{corr}/3 \sim \tilde{v} \ell / 3$, where τ_corr is the autocorrelation time of the velocity fluctuations and we have defined a correlation length $\ell = \tilde{v} \tau _\mathrm{corr}$. Introducing the magnetic Reynolds number ${\rm Rm}_{{\rm turb}} \approx \mu _0 \widetilde{v} \ell / \eta$ of the fluctuations, the net magnetic resistivity is obtained from Equation (2) as η_turb ∼ η(1  +  Rm_turb). Compared to laboratory experiments in astrophysical systems, Rm_turb ≫ 1 is usually enormous, and very large magnetic resistivities are expected. When applied to dynamo generation in the context of mean-field models, this enhanced resistivity may inhibit the magnetic field generation. It may be balanced by the α term (here mainly related to the flow helicity) which corresponds to a current generation in the direction of the background, large-scale, magnetic field—it is controversial in very turbulent systems (Hughes & Cattaneo 2008; Käpylä et al. 2009; Hughes et al. 2011; Blackman & Field 2002), in part due to a strong predicted quenching as dynamos transition from unmagnetized to magnetized states. Whatever the magnitude of the α-effect is, the existence and characterization of the β-effect and an enhanced resistivity η_turb is essential as it greatly increases the transport of magnetic fields. It is addressed here using the liquid sodium Madison Dynamo Experiment (MDE; shown in Figure 1) and related numerical modeling.

Zoom In Zoom Out Reset image size

MDE studies the role of turbulent magnetohydrodynamic processes in the onset conditions for magnetic field growth. Several laboratory experiments have generated self-sustained dynamos in turbulent flows either strongly constrained in geometry (Gailitis et al. 2001) or using ferromagnetic boundaries (Verhille et al. 2010). In many natural astrophysical and geophysical systems, like our Sun (Miesch & Toomre 2009), other stars (Brown et al. 2010), or Earth's core (Kageyama et al. 2008), the underlying flows are unconstrained. Very high Reynolds numbers and strong shear in the flow of MDE lead to vigorous turbulence. Measurements using water in a similar apparatus show that, at smaller scales, the turbulence is locally isotropic and homogenous (Nornberg et al. 2006), while at large scale it has strong poloidal and toroidal circulation (Dudley & James 1989). The experiment is operated in a regime where the magnetic field plays a limited role in the fluid dynamics and any back-reaction of the magnetic field on the flow can be neglected (Nornberg et al. 2006). Within this kinematic regime the magnetic field can be considered as a passive vector transported by the turbulent flow. In the case of strong growing magnetic fields, the back-reaction can no longer be neglected and simple parameterization models, like Equation (3), no longer apply. Although the measurement technique for observing the turbulent emf, which is used for the present studies, is still valid, the interpretation of the results requires more complex models (Bhattacharjee & Yuan 1995). Nevertheless the kinematic approach covers most important basic features in many astrophysical systems (Brandenburg & Subramanian 2005a; Ruzmaikin et al. 1989).

For the first time it is possible to directly observe all three components of the turbulent emf at a local position in the experiment. The probe used for direct measurements of the local turbulent emf (in the following paragraphs called the 3D emf probe) is based on a miniaturization (Noskov et al. 2009) of the well-known principles for velocity measurements in liquid metals by Ricou & Vives (1982). Compared to probes that have been used in other experiments (Noskov et al. 2009; Ricou & Vives 1982; von Weissenfluh 1985), our newly designed 3D emf probe, which will be described in detail in the following two paragraphs, combines a 3D velocity component measurement with a simultaneous measurement of all three magnetic components.

For each of the three directions of the velocity, radial r, latitudinal θ, and longitudinal ϕ, the potential difference between two silver-coated copper electrodes which hold a small NdFeB permanent magnet (size: 2 × 2 × 10 mm³, surface field: 0.2 T) in between, is measured simultaneously (Figure 2). Due to the strong local magnetic field of the permanent magnet $\boldsymbol{B}^\mathrm{pm}$, which is two orders of magnitude higher than the background field, the potential difference $\Phi = \int ^{P1}_{P2}(\boldsymbol{V}^\mathrm{meas}\times \boldsymbol{B}^\mathrm{pm})\,{\cdot}\, \rm {\boldsymbol{d}}\boldsymbol{l}$ yields a direct measurement of the fluctuations and time-averaged mean values of the flow components (von Weissenfluh 1985; Noskov et al. 2009) $\boldsymbol{V}^\mathrm{meas} = \langle \boldsymbol{V}\rangle+\boldsymbol{\widetilde{v}}$ for frequencies smaller than the system-based cutoff frequency f_cs ≫ 1/(μ₀σd²) (Noskov et al. 2009). Here f_cs ≈ 80 kHz with d = 1 mm, which is a typical length for changes of the strong local magnetic field given by the size of the permanent magnets used. Compared to alternative methods for flow measurements in liquid metals (e.g., applying strong global magnetic fields, where the relationship between the measured potential and flow becomes uncertain, imposing a local magnetic field with a permanent magnet yields a direct approximation of f_cs which, for the present work, is well above the relevant driving frequencies in the flow (Reuter et al. 2011). P1 and P2 are the positions of the two electrodes and their distance is l = 3 mm. As in the hot wire technique, the distance between the electrodes sets the spatial resolution of the measurement, which leads to a cutoff frequency (Bolonov et al. 1976) of f_co = 1.5F(R/l)^(2/3) ≈ 0.14–1.4 kHz with the rotation frequency of motors F = 3–30 Hz and the radius of the sphere R = 0.5 m. f_co is still about 1–2 orders of magnitude higher than typical driving frequencies in the flow. The measured potential differences are amplified with an amplifier type AM502 and processed by 16-bit digitizers on PC-based data acquisition cards with a sample rate of 1 kHz per channel. The signal-to-noise ratio of the velocity measurements is S/N_V ≈ 10². The time-resolved signals are filtered by a standard second-order Butterworth filter at 15 Hz and the resulting mean velocities are averaged over the length of the electrode.

Zoom In Zoom Out Reset image size

The tip of the 3D emf probe also holds a set of magnetic Hall sensors (4 cm away from the latitudinal and longitudinal electrodes; Figure 2), which measure the 3D mean and fluctuating parts of the magnetic field $\boldsymbol{B}^\mathrm{meas} = \langle \boldsymbol{B}\rangle+\boldsymbol{\widetilde{b}}$. These Hall sensors are far enough from the probe tip to neglect the induced field due to the advection of the magnetic field of the small permanent magnet, but well within the magnetic diffusion length of about 10 cm (Nornberg et al. 2006). The signal-to-noise ratio of the magnetic measurements is S/N_B ≈ 10⁴. Simultaneous measurements of $\boldsymbol{\widetilde{v}}$ and $\boldsymbol{\widetilde{b}}$ allow us to obtain the local turbulent emf directly.

In addition to the single 3D emf probe described above, magnetic fields $\boldsymbol{B}$ in MDE are measured by about 300 Hall sensors inside and on the surface of the experiment. Their positions can be seen in Figure 1(a). To determine the local current density $\langle \boldsymbol{J}\rangle$ the derivatives of $\langle \boldsymbol{B}\rangle$ are needed. In an axisymmetric spherical geometry it is common to convert the magnetic and velocity fields from a spatial domain to a spectral domain by decomposing them into vector spherical harmonics (Dudley & James 1989) represented by

$$\begin{eqnarray} \boldsymbol{B}(r,\theta ,\phi) &=& \sum \limits _i \nabla \times \nabla \times S_i(r) Y_{\ell _i}^{m_i}(\theta ,\phi) \boldsymbol{r} \nonumber\\ && + \nabla \times T_i(r) Y_{\ell _i}^{m_i}(\theta ,\phi) \boldsymbol{r}. \end{eqnarray} \tag{ 4 }$$

$\boldsymbol{B}(r,\theta ,\phi)$ expands in poloidal and toroidal vector fields, S_i(r) and T_i(r), with $Y_{\ell _i}^{m_i}(\theta ,\phi)$ being spectral harmonics, where l and m describe the latitudinal and longitudinal mode number, respectively. The measured fields are used to constrain radial profiles of S_i(r) and T_i(r) that are approximated by low-order splines in radius. The reconstructions are truncated to a spectral resolution of l = 7. The geometry is found experimentally to be statistically axisymmetric; thus only m = 0 harmonics are used. From Equation (4) the current is found as

$$\begin{equation} \langle \boldsymbol{J}\rangle=-\nabla \times \nabla ^2 S \boldsymbol{r}+\nabla \times \nabla \times T \boldsymbol{r}. \end{equation} \tag{ 5 }$$

In addition $\langle \boldsymbol{B}\rangle$ can be directly computed from the kinematic response of the system to an externally applied magnetic field, assuming that the velocity field is known and that the turbulent emf is a small correction. The predicted $\langle \boldsymbol{B}\rangle$ from the kinematic calculation is also consistent with the Hall probe measurements.

Figure 1(b) shows three example time traces for the radial flow (top), longitudinal magnetic field (center), and latitudinal turbulent emf (bottom). The data were taken with an externally applied axial dipole field of 50 G at Rm^tip = 160 (i.e., the maximal Rm given at the tip of the impeller). The corresponding mean values (time-averaged over 60 s) and standard deviations are given next to each time trace. The correlation of the fluctuating flow and magnetic field yields the turbulent emf directly. The component of the turbulent emf depicted is averaged by using the magnetic diffusion time τ_σ = μ₀σR² ≈ 3 s (thick black line in $\boldsymbol{\cal E}_{\theta }$) as the smoothing parameter. All three signals show high fluctuation level compared to the mean values, i.e., σ_r/〈V_r〉 ≈ σ_ϕ/〈B_ϕ〉 ≈ 30% for the radial velocity and longitudinal magnetic field components shown. In the case of the latitudinal component of the emf $\boldsymbol{\cal E}_{\theta }$, the fluctuations are almost 3.5 times higher compared to the mean value. Similar very strong turbulent fluctuations and small non-zero mean values are also found for the two remaining components ${\cal E}_r, {\cal E}_{\phi }$ (not shown here).

A turbulent emf had previously been inferred from the mean-field response to applied seed fields in MDE. A combined analysis of magnetic data, taken in MDE, and laser Doppler velocimetry data, recorded in a similarly sized water experiment, yielded an estimate of $\boldsymbol{\cal E}$ which was of the same order of magnitude as the mean flow induction $\langle \boldsymbol{V}\rangle \times \langle \boldsymbol{B}\rangle$(Spence et al. 2007). There was strong evidence that velocity fluctuations generating $\boldsymbol{\cal E}$ occurred at the system scale. In the situation studied experimentally here, the system-scale fluctuations have been strongly reduced by introduction of an equatorial baffle (Kaplan et al. 2011). The equatorial baffle reduces the amplitude of the largest-scale turbulent eddies, but it also now provides the scale separation needed for the mean-field ansatz used in Equation (3) to describe the role of turbulent fluctuations. With the 3D emf probe all three components of $\boldsymbol{V}, \boldsymbol{B}$, and $\boldsymbol{\cal E}$ are now directly measured. The ratio $\langle \boldsymbol{V}\rangle \times \langle \boldsymbol{B}\rangle/\boldsymbol{\cal E} \gtrsim 10$ for 0 < Rm^tip < 160 confirms that the turbulent emf is more than an order of magnitude smaller compared to the mean-field emf after installing the equatorial baffle.

Figure 3(a) shows the angle between the unit vector of the turbulent emf with respect to the unit vector of the magnetic field $\angle (\boldsymbol{\cal E}, \langle \boldsymbol{B}\rangle)$ (dashed line) as well as with respect to the unit vector of the corresponding local current $\angle (\boldsymbol{\cal E}, \langle \boldsymbol{J}\rangle)$ (solid line), where $\langle \boldsymbol{J}\rangle$ is obtained from Equation (5). With increasing Rm^tip, $\boldsymbol{\cal E}$ becomes almost orthogonal to $\langle \boldsymbol{B}\rangle$ and anti-parallel to $\langle \boldsymbol{J}\rangle$. The 3D vector diagram in Figure 3(b) (shown for Rm^tip = 140) indicates that the measured turbulent emf $\boldsymbol{\cal E}$ (thick red arrow) almost entirely describes a vector anti-parallel to $\langle \boldsymbol{J}\rangle$ (black arrow). The figure also includes the results of a numerical simulation, $\boldsymbol{\cal E}^{\rm sim}$ (thin light red arrow), in which the turbulent emf is computed using a parallelized version of the magnetohydrodynamic ${\tt DYNAMO}$ code (Reuter et al. 2011), which solves numerically the induction equation and Navier–Stokes equation in an incompressible electrically conducting fluid including magnetic diffusivity. An accurate numerical copy of the two counter-rotating impellers, as used in MDE, generates a similar two-vortex flow collinear to the motor axis. The numerical simulations are done at Rm = 40 and dipolar seed fields of 20 G. Time traces of the magnetic and velocity fluctuations are given at the position of the 3D emf probe. The turbulent emf $\boldsymbol{\cal E}^\mathrm{sim}$,

$$\begin{equation} \boldsymbol{\cal E}^\mathrm{sim} \equiv \langle \boldsymbol{\widetilde{v}^\mathrm{sim}}\times \boldsymbol{\widetilde{b}^\mathrm{sim}}\rangle, \end{equation} \tag{ 6 }$$

as depicted in Figure 3(b), is obtained by using the same techniques as for the experimental data. Considering that the fluid Reynolds number for the simulations (Re ⩽ 2000) is several orders of magnitude lower compared to MDE (Re ≈ 10⁷), it is remarkable that the resulting simulated turbulent emf $\boldsymbol{\cal E}^{\rm sim}$ aligns well with the measured one. Hence, measurement and numerical simulation clearly show that the turbulent emf, in the kinematic regime considered, is dominated by the second term on the right-hand side of Equation (3), which describes the β-effect.

Zoom In Zoom Out Reset image size

This conclusion is also confirmed quantitatively. The directly measured velocity fluctuations $\widetilde{v}$ and autocorrelation times τ_corr give $\beta =\widetilde {v}^{\,2} \tau _\mathrm{corr}/3$ for different Rm^tip (Table 1). Together with the current determined from the magnetic reconstruction, one can compute the diffusive term $\beta \mu _0 \langle \boldsymbol{J}\rangle$ in Equation (3), which is shown in Figure 4(a), red. One observes that, within the accuracy of the estimation, this diffusive term accounts for the majority of the directly measured turbulent emf $||\boldsymbol{\cal E}||$ (Figure 4(a), black). A rough estimate for the local α-effect due to flow helicity (the first term in Equation (3)) can be determined by a linear fit of the longitudinal component ${\cal E}_{\phi }$ as a function of the locally measured longitudinal component B_ϕ for different Rm^tip (Figure 4(b) and Table 1). Including the estimated α-effect in Equation (3), represented by the blue squares in Figure 4(a), does not change the overall trend and confirms the dominance of the β-effect. It is noted that up to the present day no self-excited magnetic field growth has been observed in MDE. In order to achieve dynamo action further experiments including stronger motors for driving the impellers and extra sets of rotatable baffles (in addition to the previously mentioned equatorial baffle) to optimize the ratio between poloidal and toroidal flows and to increase the flow helicity are planned.

Zoom In Zoom Out Reset image size

Table 1. The Measured Values of $\tilde{v}, \tau _\mathrm{corr}, \beta$, and α^fit for Different Rm^tip used in Figure 4(a) to Calculate the Corresponding Terms of Equation (3)

Rmtip	$\widetilde{v}$	τcorr	β	αfit
	(m s−1)	(s)	(m2 s−1)	(m s−1)
60	0.55	0.025	0.002	−0.029
100	0.82	0.047	0.01	−0.031
140	1.34	0.037	0.02	−0.034
160	1.74	0.032	0.03	−0.048

Download table as:  ASCIITypeset image

In summary, this work presents direct observations of the 3D turbulent emf in a turbulent flow of liquid sodium. The measurements support the ansatz of an enhanced eddy resistivity predicted by simple mean-field theory models. This is the first time such a measurement has been possible in a laboratory setting, as described here. Future studies of the turbulent emf using multiple arrays of 3D emf probes are in preparation. These and other forthcoming experimental measurements of the global structure of MHD turbulence will provide detailed insight into key questions addressing the effect of large-scale and small-scale helicity (α-effect) and the role of molecular diffusivity in mediating the turbulent transport of magnetic fields.

The measurements discussed here were taken in a laboratory experiment, but the general nature of the findings has great impact for our understanding of the turbulent transport of vector quantities within astrophysical objects. In particular, for isotropic turbulence where the magnetic stresses are weak, these measurements strongly support simple mean-field closure methods that have been of vital importance in the modeling of magnetic transport in astrophysics, particularly for the dynamo problem (Blackman & Field 2002; Brandenburg & Subramanian 2005b). The turbulent transport of magnetic fields likely also plays a vital role in planet and star formation, and in MHD dynamics on galactic scales. Just such an enhanced magnetic diffusion may be essential for setting the solar activity cycle (Charbonneau 2010) and also the rate of star formation in the magnetic interstellar medium (Gaensler et al. 2011). Turbulence in astrophysical settings can be significantly non-isotropic or dominated by magnetic stresses, and those parameter regimes are a direction for future experiments.

The authors thank Ingrid Reese, John Wallace, and Paul Brooks for technical assistance and probe work at the MDE. This project is funded by the National Science Foundation and is a member experiment of the Center for Magnetic Self Organization in Laboratory and Astrophysical Plasmas (CMSO). B.P.B. is supported in part by NSF Astronomy and Astrophysics postdoctoral fellowship AST 09-02004. CMSO is supported by NSF grant PHY 08-21899.