ABSTRACT
Recent studies on the Galactic supernova remnant (SNR) G344.7–0.1 have commonly claimed its origin to be a core-collapse supernova (SN) explosion, based on its highly asymmetric morphology and/or proximity to a star-forming region. In this paper, however, we present an X-ray spectroscopic study of this SNR using Suzaku, which is supportive of a Type Ia origin. Strong K-shell emission from lowly ionized Fe has clearly been detected, and its origin is determined, for the first time, to be the Fe-rich SN ejecta. The abundance pattern is highly consistent with that expected for a somewhat-evolved Type Ia SNR. It is suggested, therefore, that the X-ray point-like source CXOU J170357.8–414302 located at the SNR's geometrical center is not associated with the SNR but is likely to be a foreground object. Our result further indicates that G344.7–0.1 is the first possible Type Ia SNR categorized as a member of the so-called mixed-morphology class. In addition, we have detected emission from He-like Al at ∼1.6 keV, the first clear detection of this element in the spectrum of an extended X-ray source. The possible enhancement of the Al/Mg abundance ratio from the solar value suggests that the ambient interstellar medium has a relatively high metallicity (not less than 10% of the solar value). We also report the marginal detection of Cr and Mn, although the measured fluxes of these lines have large statistical and systematic uncertainties.
1. INTRODUCTION
The supernova remnant (SNR) G344.7–0.1 was discovered in radio observations (Caswell et al. 1975) and exhibits largely asymmetric structure with a diameter of ∼10' and a bright western part (Dubner et al. 1993; Whiteoak & Green 1996). In X-rays, the SNR was first identified by the ASCA Galactic Plane Survey (Sugizaki et al. 2001). Yamauchi et al. (2005) found that the ASCA spectrum can be reproduced by an optically thin thermal plasma with an electron temperature of ∼1 keV. Owing to the limited photon statistics, however, they could not determine whether the plasma had achieved collisional ionization equilibrium (CIE) or was still in non-equilibrium ionization (NEI). Another interesting result from ASCA was the possible detection of Fe-Kα emission with an energy of 6.4 (±0.2) keV. Its origin was suggested to be either fluorescence from cold dense clouds or low-ionized plasma, but was not definitively determined.
The X-ray morphology of the SNR was examined in detail during Chandra and XMM-Newton observations. The emission correlates relatively well with the radio structure (Combi et al. 2010), but the X-ray peak is located more interior with respect to that in the radio (Giacani et al. 2011). It was argued that the irregular morphology of this SNR may be due to expansion through a dense interstellar medium (ISM) with a density gradient toward the western part. Giacani et al. (2011) suggested that this dense environment interacting with the SNR's shock is a plausible counterpart of the unidentified TeV γ-ray source HESS J1702–420 (Aharonian et al. 2008). Notably, Combi et al. (2010) discovered a point-like source, CXOU J170357.8–414302, at the geometrical center of the SNR with no significant extended emission to indicate a pulsar wind nebula. The source was, therefore, suggested to be a possible candidate for a compact central object (CCO) physically associated with the SNR. However, the absorption column of the point source was found to be significantly smaller than that of the SNR, implying that the source is a foreground object. In fact, the infrared/optical object coinciding with CXOU J170357.8–414302 exhibits typical characteristics of an early-K star (Combi et al. 2010).
The progenitor of G344.7–0.1 is currently not well identified, but most of the previous works are supportive of a core-collapse (CC) origin, based mainly on its associations with a nearby molecular cloud or a wind-blown bubble (Combi et al. 2010; Giacani et al. 2011). In fact, infrared emission from shocked molecular gas has been observed in this SNR, which is more common in CC SNRs than in Type Ia remnants (Reach et al. 2006; Andersen et al. 2011). Furthermore, it has recently been argued that its highly asymmetric X-ray morphology is somewhat similar to other CC SNRs (Lopez et al. 2011). In these studies, however, the abundances of heavy elements could not be measured accurately, and the detection of the Fe K-shell emission was not clear or only marginal. Since production of Fe (56Ni, before nuclear decay) is significantly different between CC and Type Ia supernovae (SNe; e.g., Iwamoto et al. 1999), clear detection and diagnostics of the Fe emission as well as accurate measurements of the elemental abundances could help resolve the nature of its progenitor and environment.
In this paper, we present the results of the Suzaku observation of G344.7–0.1, utilizing its high spectral sensitivity especially in the Fe K-shell X-ray (6–7 keV) band. The errors quoted in the text and tables are at the 90% confidence level, and the error bars given in the spectra are for 1σ confidence, unless otherwise stated.
2. OBSERVATION AND RESULTS
G344.7–0.1 was observed by Suzaku on 2007 February 21, using X-ray imaging spectrometers (XISs). Each XIS consists of three active X-ray sensors. Two of them are installed with front-illuminated (FI) sensors, while the other is installed with a back-illuminated (BI) sensor. We used the standard tools of HEADAS version 6.11 for the data reduction. The archival data were reprocessed with the calibration database released on 2011 August 11 and reduced in accordance with the recommended screening criteria.5 The total effective exposure time after the screening was about 44 ks. Only grade 0, 2, 3, 4, and 6 events were used in the following analysis.
2.1. Imaging Analysis
In Figure 1, we present narrowband images of the SNR in the energy ranges of (a) 0.7–1.2 keV, (b) 1.81–1.90 keV, (c) 2.41–2.51 keV, (d) 4.2–6.0 keV, and (e) 6.34–6.57 keV (hereafter "soft," "Si-K," "S-K," "hard," and "Fe-K," respectively). In the soft image, we can see a point-like source located nearly at the center of the remnant. The peak position of the source is (R.A., decl.)J2000.0 = (17h03m56s, −41°42'56''), consistent with the location of CXOU J170357.8–414302 within the position uncertainty of the XIS (∼1'; Uchiyama et al. 2008).
Figure 1. XIS images of G344.7–0.1 in the energy bands of the soft continuum ((a) 0.7–1.2 keV), Si-K ((b) 1.81–1.90 keV), S-K ((c) 2.41–2.51 keV), hard continuum ((d) 4.2–6.0 keV), and Fe-K ((e) 6.34–6.57 keV), and the equivalent-width map of the Fe-K emission (f). North is up and east is to the left. The scale is linear. Intensity contours for the MOST 843 MHz radio emission (Whiteoak & Green 1996) are shown in the images (a) and (b), whereas those for the Si-K emission are overlaid on the images (c), (d), (e), and (f). The regions used in the spectral analysis are indicated in (b); the green circle is centered on the position (R.A., decl.)J2000 = (17h03m50 7, −41°42'41'').
7, −41°42'41'').
Download figure:
Standard image High-resolution imageTo compare the surface brightness distribution among the different energy bands, intensity contours for the Si-K emission are superimposed on the images in Figures 1(c)–(f). The spatial profiles of the S-K and hard continuum emission are highly correlated with the Si-K image, whereas the peak of the Fe-K emission is slightly shifted toward the south. An equivalent-width (EW) map for the Fe-K line is shown in Figure 1(f), where the continuum level was estimated by scaling the hard image with a bremsstrahlung model fitting for the 4.2–6.0 keV spectrum. The Fe-K EW is enhanced at the southeastern part of the remnant, and not spatially correlated with the Si-K emission.
2.2. Spectral Analysis
We extracted the XIS spectra of the entire SNR from a circular region with a radius of 3 2 (shown in Figure 1(b)), but the central point source was excluded. The two FI spectra were summed up to improve the photon statistics, since their characteristics are almost identical. The background data were taken from an annulus surrounding the SNR with inner and outer radii of 5
2 (shown in Figure 1(b)), but the central point source was excluded. The two FI spectra were summed up to improve the photon statistics, since their characteristics are almost identical. The background data were taken from an annulus surrounding the SNR with inner and outer radii of 5 0 and 7
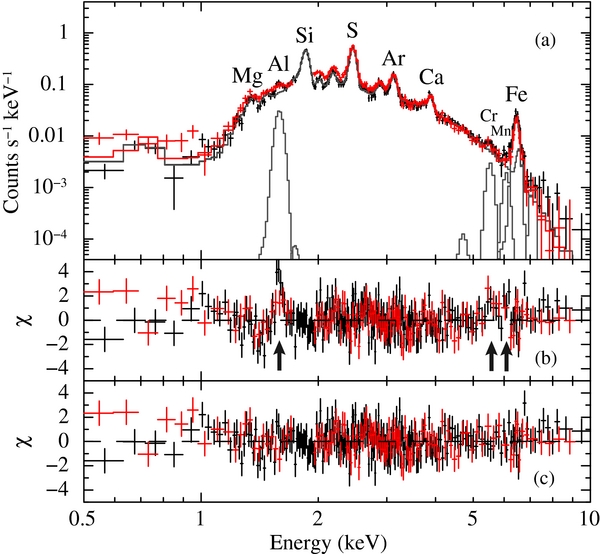
0 and 7 0, respectively. The resultant spectra are shown in Figure 2(a). We see the Fe-Kα line detected with good statistics. Using XSPEC (Arnaud 1996), we first fitted the spectra with an absorbed NEI plasma model, wabs × vnei (K. Borkowski6). The free parameters were the absorption column density (NH), electron temperature (kTe), ionization timescale (net), volume emission measure (VEM), and elemental abundances of Mg, Si, S, Ar, Ca, and Fe relative to the solar values of Anders & Grevesse (1989). The photoelectric absorption cross sections were taken from Morrison & McCammon (1983). The gain calibration of the XIS is known to be problematic around the energy of the neutral Si K-edge (e.g., Yamaguchi et al. 2009). Therefore, we ignore the energy range of 1.75–1.90 keV in the BI spectrum, similar to Yamaguchi et al. (2009). In addition, a significant inconsistency between the FI and BI data was found below 1 keV. Although we also attempted to use background data from a blank sky region and pure non-X-ray background data, instead of the data taken from the outer annulus region, the inconsistency remained in all cases. We conclude that the problem is not caused by the background subtraction but is due to issues related to the source spectra. One of the possible origins is an incomplete calibration of the thickness of contamination material accumulated on the optical blocking filters of the XIS (Koyama et al. 2007). Although this is not definitive, we excluded the data below 1.0 keV from the following analysis.
0, respectively. The resultant spectra are shown in Figure 2(a). We see the Fe-Kα line detected with good statistics. Using XSPEC (Arnaud 1996), we first fitted the spectra with an absorbed NEI plasma model, wabs × vnei (K. Borkowski6). The free parameters were the absorption column density (NH), electron temperature (kTe), ionization timescale (net), volume emission measure (VEM), and elemental abundances of Mg, Si, S, Ar, Ca, and Fe relative to the solar values of Anders & Grevesse (1989). The photoelectric absorption cross sections were taken from Morrison & McCammon (1983). The gain calibration of the XIS is known to be problematic around the energy of the neutral Si K-edge (e.g., Yamaguchi et al. 2009). Therefore, we ignore the energy range of 1.75–1.90 keV in the BI spectrum, similar to Yamaguchi et al. (2009). In addition, a significant inconsistency between the FI and BI data was found below 1 keV. Although we also attempted to use background data from a blank sky region and pure non-X-ray background data, instead of the data taken from the outer annulus region, the inconsistency remained in all cases. We conclude that the problem is not caused by the background subtraction but is due to issues related to the source spectra. One of the possible origins is an incomplete calibration of the thickness of contamination material accumulated on the optical blocking filters of the XIS (Koyama et al. 2007). Although this is not definitive, we excluded the data below 1.0 keV from the following analysis.
Figure 2. (a) XIS spectra of the entire SNR. Black and red represent the FI and BI spectra, respectively. Individual components of the best-fit model are shown with gray lines. Panels (b) and (c) display the residuals from the models without and with the Gaussian components of Al-Kα, Cr-Kα, and Mn-Kα, respectively. Note that the energies below 1.0 keV are ignored from the spectral fitting.
Download figure:
Standard image High-resolution imageThe model described above gave a good fit to the emission lines at energies below 4 keV and the overall continuum spectrum, but failed to reproduce the Fe-Kα line profile; the peak energy was lower in the data than in the model. Although we temporarily used a plane-parallel shock model (vpshock; Borkowski et al. 2001) instead of the simple vnei model, no significant improvement was achieved. This implies that the residual Fe-Kα emission arises from either another plasma component with a lower ionization timescale or fluorescence of neutral matter. To reveal its nature, we examined the Fe-Kα line parameters with an additional Gaussian model. Hereafter, the Fe abundance in the vnei component was fixed to unity, as for the other fixed parameters (C, N, O, and Ne). The center energy and EW of the additional Fe-Kα component were obtained to be 6.44 (±0.01) keV and 3.7 (±0.4) keV, respectively. Since the former value is significantly different from the energy of Kα emission from neutral Fe (6.40 keV), we can safely reject the fluorescence scenario. Furthermore, the EW corresponds to an Fe abundance higher than 10 solar for any electron temperature, implying that the predominant origin of the emission is likely to be the ejecta rather than the ISM. Interestingly, the measured Fe-Kα centroid is fully consistent with that observed in Tycho's SNR (Tamagawa et al. 2009), suggesting a similar ionization state of Fe in both SNRs. Tamagawa et al. (2009) also reported the detection of the Fe-Kβ line in the Suzaku spectrum of Tycho's SNR, with Kβ/Kα intensity ratio of ∼0.05. We followed this result to add another Gaussian at 7.11 keV by assuming the same intensity ratio. The best fit thereby obtained had kTe = 1.0 keV and χ2/dof = 410/309. The residual with this model is shown in Figure 2(b).
Although the fit is now almost acceptable, a prominent line-like residual is still observed at ∼1.6 keV (in both the FI and BI spectra). We tried two-component vnei models, but this residual did not disappear even with independent free parameters including abundances between the components. Given that the vnei component already takes into account the Kβ emission of Mg xi (1.58 keV), the most likely origin of this feature is Al xii Kα blend (e.g., 1.60 keV for the resonance line) that is not included in the vnei code in XSPEC. Introducing a Gaussian to account for this emission, we achieved a significant reduction in the χ2/dof value (from 410/309 to 354/306). In addition, we still see small residuals at ∼5.5 keV and ∼6.1 keV (indicated by black arrows in Figure 2(b)), possibly due to Cr- and Mn-Kα emissions, respectively. Adding a Gaussian for the former resulted the reduction in χ2 of 15, while that for the latter resulted the additional reduction of 9. The best-fit parameters and residuals from the model obtained after adding these emission features are given in the "Model Ax" column in Table 1 and Figure 2(c), respectively.
Table 1. Spectral Parameters
| Component | Parameter | Model Ax | Model Bx | Model As | Model Bs |
|---|---|---|---|---|---|
| Absorptiona | NH (1022 cm−2) | 4.7+0.2−0.2 | 5.1+0.3−0.3 | 4.6+0.1−0.1 | 4.6+0.2−0.1 |
| NEI plasmab | kTe (keV) | 0.98+0.04−0.03 | 0.92+0.04−0.04 | 1.01+0.04−0.04 | 0.96+0.05−0.06 |
| Mg (solar) | 0.52+0.18−0.15 | 0.87+0.37−0.30 | 0.66+0.18−0.15 | 0.60+0.17−0.14 | |
| Al (solar) | ... | ... | 1.9+0.5−0.4 | 1.6+0.4−0.4 | |
| Si (solar) | 1.1+0.1−0.1 | 1.3+0.2−0.2 | 1.3+0.1−0.1 | 1.1+0.1−0.1 | |
| S (solar) | 1.9+0.1−0.1 | 2.0+0.1−0.1 | 2.2+0.1−0.1 | 2.0+0.1−0.1 | |
| Ar (solar) | 2.0+0.2−0.2 | 2.1+0.2−0.2 | 2.3+0.2−0.2 | 2.2+0.2−0.2 | |
| Ca (solar) | 2.2+0.2−0.2 | 2.2+0.3−0.3 | 2.8+0.4−0.4 | 2.7+0.4−0.4 | |
| net (1011 cm−3 s) | 1.7+0.2−0.2 | 2.2+0.5−0.3 | 1.2+0.2−0.2 | 1.3+0.2−0.2 | |
| VEM (1012 cm−5)c | 7.0+0.7−0.8 | 8.0+0.9−0.9 | 6.1+0.7−0.5 | 7.2+1.0−0.8 | |
| Fe ejecta | E (eV) | 6447+11−12 | ... | 6455+11−11 | ... |
| kTe (keV) | ... | 3.6+1.2−0.8 | ... | 2.8+7.0−0.7 | |
| net (109 cm−3 s) | ... | 9.3+2.2−2.0 | ... | 7.2+1.5−1.1 | |
| σ (eV) | 78+18−20 | 67+18−23 | 85+20−22 | 75+17−19 | |
| Normalizationd | 2.8+0.3−0.3 | 1.4+1.2−0.6 | 3.0+0.3−0.3 | 2.2+3.5−1.5 | |
| Al-Kα | E (eV) | 1585+10−9 | 1585+9−10 | ... | ... |
| σ (eV) | 8+21−8 | 12+24−12 | ... | ... | |
| Flux (10−4 photons cm−2 s−1) | 3.7+1.2−1.0 | 5.6+2.5−1.7 | ... | ... | |
| Cr-Kαe | E (eV) | 5526+70−66 | 5524+72−69 | 5530+76−68 | 5527+80−71 |
| Flux (10−6 photons cm−2 s−1) | 3.6+1.6−1.4 | 3.4+1.5−1.5 | 3.6+1.7−1.5 | 3.3+1.5−1.5 | |
| Mn-Kαe | E (eV) | 6085+107−120 | 6106+117−126 | 6076+113−126 | 6088+121−131 |
| Flux (10−6 photons cm−2 s−1) | 2.4+1.2−1.3 | 2.4+1.7−1.4 | 2.3+1.4−1.4 | 2.2+1.5−1.4 | |
| χ2/dof | 330/302 | 319/301 | 370/304 | 362/303 | |
Notes. aThe absorption cross sections were taken from Morrison & McCammon (1983). bSolar abundances of Anders & Grevesse (1989) are assumed. The values for C, N, O, Ne, Fe, and Ni are fixed to unity. cVolume emission measure, ∫nenHdV/(4πD2), where V and D are the emitting volume (cm3) and distance to the source (cm), respectively. dFlux (10−5 photons cm−2 s−1) for Models Ax/As and ∫nenFedV/(4πD2) (108 cm−5) for Models Bx/Bs. eGaussian widths are linked to that of the Fe-Kα line.
Download table as: ASCIITypeset image
As a final step, we replaced the 6.44 keV Gaussian (Fe-Kα) with a vnei model which consists purely of Fe ions and electrons, because the Fe-rich ejecta may contribute to the L-shell emission as well. We found that the Fe-Kα line is broadened to a width greater than that expected for a single vnei or vpshock model, and thus introduced a gsmooth model to convolve the second vnei (Fe-ejecta) component with a Gaussian with a finite width. In addition, since the vnei model does not include the Fe-Kβ line data, we left the 7.11 keV Gaussian by fixing its flux to the best-fit value from Model Ax. The resultant spectral model is shown in Figure 3, and the best-fit parameters are given in the "Model Bx" column in Table 1. All the values are consistent with those in Model Ax within the statistical errors. This implies that neither uncertainty in Fe L-shell emissivity nor an electron temperature of the Fe-ejecta component crucially affects the abundance measurement.
Figure 3. Same as Figure 2, but a pure Fe plasma model is used instead of the Fe-Kα Gaussian. The model components with solid lines and residuals are for Model Bx. The blue dotted line indicates the contribution of the Fe-ejecta component in the best fit of Model Bs. The Fe L-shell flux is weaker than that in Model Bx.
Download figure:
Standard image High-resolution imageWe further analyzed the spectrum with the same procedure but using the SPEX software package (Kaastra et al. 1996), so as to estimate the systematic uncertainties in the results as carefully as possible. Since the NEI model in SPEX includes the Al K-shell emission, the Gaussian at 1.6 keV was removed. The results are given in the columns of "Model As" and "Model Bs" in Table 1. Again, no significant variation is found among the results with different models or atomic codes. The contribution of the Fe-ejecta component in Model Bs is shown as a blue dotted line in Figure 3. We found that the emissivity ratio of the Fe L-shell to K-shell emissions is generally given to be lower in SPEX for an identical electron temperature. This makes limits of the temperature and normalization more difficult to determine in Model Bs, since the temperature of the Fe-ejecta component is mainly determined by the Fe L-shell-to-K-shell intensity ratio.
The elemental abundances of the first vnei component ("NEI plasma" in Table 1) are moderately higher than the solar values, with the exception of Mg, suggesting the origin of this component to be a mixture of the ejecta and swept-up ISM. This interpretation will be discussed more quantitatively in Section 3.2.
3. DISCUSSION AND CONCLUDING REMARKS
3.1. Distance to the SNR
The distance to G344.7–0.1 is highly uncertain, despite its importance for determination of the SNR's physical properties. It had once been estimated to be ∼14 kpc from the Σ–D relation (Dubner et al. 1993), but this phenomenological method is notoriously unreliable with large intrinsic dispersion. Based on H i absorption and emission features possibly associated with the SNR, Giacani et al. (2011) recently estimated a distance of 6.3 (±0.1) kpc. However, this estimate is also uncertain (see Hayato et al. 2010 and references therein for the case of the Tycho's SNR), and is suspected to be unreasonably small due to the following reasons.
We have obtained a foreground absorption column density of NH = (4.5–5.4) × 1022 cm−2 (Table 1), which is consistent with all previous results (Yamauchi et al. 2005; Combi et al. 2010; Giacani et al. 2011). According to the DL map (Dickey & Lockman 1990) and the LAB map (Kalberla et al. 2005), the total Galactic H i column density N(H i) toward the direction of G344.7–0.1 is given to be 1.8 × 1022 cm−2 and 1.5 × 1022 cm−2, respectively. It is known that averaged number densities of molecular hydrogen and neutral atomic hydrogen are comparable with each other in the Galactic plane, while that of ionized hydrogen is negligibly small (e.g., Ferrière 2001). We hence obtain a total Galactic hydrogen column density of N(total) = N(H i) + 2N(H2) = (4.5–5.4) × 1022 cm−2. This value is fully consistent with the measured absorption column for G344.7–0.1, suggesting that the SNR is situated near the opposite edge of the Galactic plane, or at least farther than the Galactic tangent point of this direction (8.2 kpc; a distance to the Galactic center is assumed to be 8.5 kpc). In fact, the distances to SNRs CTB 37A (G348.5+0.1) and CTB 37B (G348.7+0.3), located in a similar direction, are respectively known to be ∼11 kpc (Reynoso & Mangum 2000) and ∼10 kpc (Caswell et al. 1975), but have smaller NH values of (3–4) × 1022 cm−2 (Sezer et al. 2011; Nakamura et al. 2009). Although Giacani et al. (2011) also performed similar estimates to support their claim, they assumed that 2/3 of the total Galactic hydrogen (and associated heavy elements) is distributed in the SNR's foreground. This assumption is quite unreasonable, given that the claimed distance of 6.3 kpc is closer than the Galactic tangent point. Therefore, the distance to the SNR is assumed to be 14 kpc in the following discussion, even though this value is not definitive either.
3.2. Fe Emission and Possible Progenitor
We have clearly detected strong Fe K-shell emission and determined its origin to be the SN ejecta, for the first time. The Fe ejecta can be characterized by a pure-metal plasma whose electron temperature and ionization timescale are different from those of the other plasma component with abundant α-elements (i.e., Mg, Si, S, Ar, and Ca). Combi et al. (2010) argued that the wideband X-ray spectrum, including the Fe-Kα emission, can be well represented by a one-component vpshock model with kTe = 1.17 keV and τu (a maximum value of ionization timescales) = 2.5 × 1011 cm−3 s. However, photon statistics of the Chandra and XMM-Newton data are too low around the Fe-Kα emission to independently determine its center energy. We found that the vpshock model applied by Combi et al. (2010) predicts an Fe-Kα centroid of ∼6.57 keV. This value is significantly higher than the energy derived from the Suzaku spectra, and hence at least two components are absolutely needed.
In addition to the plasma condition, the emitting volumes of both components are also likely to be different from each other (see Figure 1). Therefore, direct comparison of the abundances (and hence masses) among the Fe and α-elements is not straightforward, although this comparison is the most credible way to distinguish the SN type. However, we should note that strong Fe emission is observationally very common in Type Ia SNRs and is unusual in CC SNRs (e.g., Hughes et al. 1995). Furthermore, the ionization timescale for the Fe ejecta in G344.7–0.1 is found to be about one order of magnitude lower than that for the other elements (Table 1), which is another typical characteristic of Type Ia SNRs (Hwang et al. 1998; Kosenko et al. 2008; Yamaguchi et al. 2008a; Badenes et al. 2003, 2007). This can be explained by a stratified ejecta composition with Fe in the interior that is theoretically expected (e.g., Gamezo et al. 2005; Maeda et al. 2010a) and has also been confirmed by optical observations of standard Type Ia SNe (e.g., Tanaka et al. 2011). Although there are a few of well-established CC SNRs (e.g., Cas A, W49B, and N132D) that exhibit relatively strong Fe K-shell emission, the Fe is highly ionized in all of them, unlike in G344.7–0.1 and other Type Ia SNRs (Maeda et al. 2009; Ozawa et al. 2009; Xiao & Chen 2008). Since highly ionized atoms generally have higher emissivity than lowly ionized ones, the large Fe flux in these CC SNRs is achieved even with relatively low abundance of this element.
The abundance pattern of the α-elements we obtained is also supportive of the Type Ia SN origin. The estimated masses of the hydrogen and α-elements for each applied model are given in Table 2, where a 3 2-radius sphere for the X-ray emitting region, with a filling factor of unity, is assumed. Here, we compare these values with yields of different SN nucleosynthesis models. Since the large hydrogen mass of ≳150 M☉ implies that the SNR is dominated by the swept-up ISM, we take into account both the ejecta and ISM contributions. The total observed mass of the hydrogen or heavy elements Z can be phenomenologically divided into those of the ejecta and ISM components as MH = MH, ej + MH, ISM or MZ = MZ, ej + MZ, ISM. (MH, ej should be 0 for Type Ia SNe.) The relation between MZ, ISM and MH, ISM is given as
2-radius sphere for the X-ray emitting region, with a filling factor of unity, is assumed. Here, we compare these values with yields of different SN nucleosynthesis models. Since the large hydrogen mass of ≳150 M☉ implies that the SNR is dominated by the swept-up ISM, we take into account both the ejecta and ISM contributions. The total observed mass of the hydrogen or heavy elements Z can be phenomenologically divided into those of the ejecta and ISM components as MH = MH, ej + MH, ISM or MZ = MZ, ej + MZ, ISM. (MH, ej should be 0 for Type Ia SNe.) The relation between MZ, ISM and MH, ISM is given as
where AZ(ISM) is the abundance of the ISM component (relative to the solar value) and the ratio mZ/mH corresponds to the average mass number of element Z. Therefore, we obtain
for each element Z. In Figure 4, we show the observed mass ratio MZ/MH of the different elements normalized by the solar values. On the other hand, theoretical values can be derived by substituting nucleosynthesis products of various SN models for MH, ej and MZ, ej in Equation 2. Here we employ the Type Ia deflagration or delayed-detonation models (Iwamoto et al. 1999) and the CC SN models with various progenitor masses (Kobayashi et al. 2006). The representative results of the comparison are shown in Figure 4, where for AZ(ISM) we consider several values in the range of 0.5–1.0 solar. We find that the abundance pattern is broadly consistent with the Type Ia models, but does not match with any CC models. We also considered several other nucleosynthesis models for CC SNe (e.g., Woosley & Weaver 1995; Thielemann et al. 1996), and reached essentially the same conclusion. Although our estimates of the element masses is largely affected by an assumed distance and a filling factor, we note that the enhanced abundance ratios of S/Mg, Ar/Mg, and Ca/Mg can be explained only by an evolved Type Ia SN. This is because no CC model predicts an Mg abundance less than a half of the heavier α-elements' abundances.
Figure 4. Elemental mass abundances relative to the solar values compared with those expected from several nucleosynthesis models for Type Ia SNe: W7 (red solid lines), WDD1 (red dashed lines), WDD2 (magenta solid lines), and WDD3 (magenta dashed lines) from Iwamoto et al. (1999), and for CC SNe with different progenitor masses of 13 M☉ (green solid lines), 15 M☉ (green dashed lines), 18 M☉ (blue solid lines), 20 M☉ (blue dashed lines), 25 M☉ (cyan solid lines), and 30 M☉ (cyan dashed lines) from Kobayashi et al. (2006). Note that contributions of the swept-up ISM are taken into account (see the text for details). The applied spectral models and assumed ISM abundances are indicated in each panel.
Download figure:
Standard image High-resolution imageTable 2. Masses of the Hydrogen and α-elements
| Element | Mass (M☉) | |||
|---|---|---|---|---|
| Model Ax | Model Bx | Model As | Model Bs | |
| H | 164 | 175 | 153 | 166 |
| Mg | 0.078 | 0.14 | 0.092 | 0.091 |
| Si | 0.18 | 0.23 | 0.20 | 0.18 |
| S | 0.16 | 0.18 | 0.17 | 0.17 |
| Ar | 0.043 | 0.048 | 0.046 | 0.048 |
| Ca | 0.033 | 0.035 | 0.039 | 0.041 |
Download table as: ASCIITypeset image
A Type Ia SNR in a dense environment (e.g., near molecular clouds) is quite rare (e.g., Andersen et al. 2011). In fact, Giacani et al. (2011) identified G344.7–0.1 as a CC SNR, based on its spatial association with H i clouds possibly created by recent (∼106 yr ago) star formation. Lopez et al. (2011) were also supportive of its CC origin, since the strong asymmetry in its X-ray morphology was analogous to other CC SNRs. However, these preceding works lacked statistically sufficient spectral information, especially of Fe emission, that is so crucial in distinguishing SN types. Similar situations have occurred with RCW 86 and N103B. RCW 86 was found to be evolving within a wind-blown bubble and thus suggested to be a CC SNR (Vink et al. 2006). Possible evidence of interaction with a molecular cloud was also pointed out in this SNR (Yamaguchi et al. 2008b). However, recent observations and a theoretical work strongly suggest its origin to be a Type Ia SN (Williams et al. 2011; Yamaguchi et al. 2011b). N103B was also initially classified as a CC SNR because of its proximity to the young star cluster NGC 1850B with an age of ∼4 Myr (Chu & Kennicutt 1988; Gilmozzi et al. 1994), but the ASCA and Chandra spectra revealed its Type Ia SN origin (Hughes et al. 1995; Lewis et al. 2003). Moreover, Badenes et al. (2009) found that the progenitor was possibly associated with star formation at 50–150 Myr ago, suggesting no direct relationship between the SNR's progenitor and NGC 1850B. It is worth noting that Lewis et al. (2003) discovered that the EW maps of Si and S K-shell emission exhibit nearly symmetric shell-like structure, in contrast to the strong east–west asymmetry in the line emission measure (i.e., plasma density). In the morphological study by Lopez et al. (2011), the symmetry of G344.7–0.1 was investigated only with the broad X-ray band image, which can be biased by density inhomogeneity in the ambient ISM. EW maps of specific elements could display an uncontaminated ejecta distribution, which could be more symmetric if G344.7–0.1 is indeed a Type Ia remnant. This will be explored in our future work combining high-resolution images of Chandra and XMM-Newton.
The point-like soft X-ray source CXOU J170357.8–414302, located at the SNR's geometrical center, has been suggested to be either a CCO associated with the SNR or a foreground K0 star (Combi et al. 2010). Since our result suggests a Type Ia origin of G344.7–0.1, the latter possibility is preferred.
From the morphological features in the radio and X-ray bands, G344.7–0.1 can be classified as a mixed-morphology (MM) SNR (Rho & Petre 1998; see also Giacani et al. 2011 who revealed the complete shell structure in the radio including the faint eastern region). Despite continuous efforts by a number of authors (e.g., White & Long 1991; Cox et al. 1999; Shelton et al. 1999; Petruk 2001; Slane et al. 2002), evolutionary characteristics that have led to the observed properties of MM SNRs are not well understood. It should be noted that all the MM SNRs for which progenitor types have been well identified are known to have CC origins. Therefore, if our conclusion about the progenitor type of G344.7–0.1 is correct, this result would demonstrate that Type Ia SNe can also form remnants of this class.7 This may support an idea that the formation mechanism of this unusual morphology is not related to the nature of progenitors, but rather associated with their environment, as was assumed in the several previous works (e.g., White & Long 1991; Shelton et al. 1999). Interestingly, recent Suzaku observations have discovered overionized plasmas in several MM SNRs (e.g., Yamaguchi et al. 2009; Ozawa et al. 2009), which are quite different from the ionization conditions in G344.7–0.1. Future works are warranted to comprehensively understand the evolution of both the morphology and ionization in MM SNRs.
The EW of the Fe-Kα emission is not uniform but is enhanced in the southeast region (Section 2.1). For more quantitative studies, we extracted spectra from two elliptical regions, "SE" and "NW" shown in Figure 1(f), and fitted with the same models as used in Section 2.2. The Fe-Kα EWs for SE and NW are 5.1 (±0.7) keV and 3.3 (±0.5) keV, respectively. If the temperature of the Fe ejecta is constant across the entire remnant, the surface brightness of the Fe emission is approximately proportional to n2Fe. Therefore, the ejecta density in the SE region may be higher than that in the NW region by a factor of ∼1.2. An inhomogeneity of hot ejecta can arise from the interaction of SNRs with nonuniform ambient matter, as was observed, for example, in Kes 27 (Chen et al. 2008); the reflected shock after the collision between the blast wave and dense ISM can propagate backward and enhance the X-ray emission from the ejecta. In the case of G344.7–0.1, however, no evidence of dense matter is found around the SE region, but the NW rim is, in contrast, likely to have encountered a molecular cloud (Combi et al. 2010). Therefore, one of the possible origins of the enhancement is an inhomogeneous ejecta distribution caused by an asymmetric SN explosion. The small asymmetry in 56Ni production with a density variation of factor ∼1.2 is within the range that can be theoretically explained by an established delayed-detonation Type Ia SN model (e.g., Maeda et al. 2010b). Alternatively, an overall SE–NW temperature gradient can explain the inhomogeneity, but unfortunately, the electron temperature of the Fe-ejecta component is difficult to constrain because of the relative weakness of its bremsstrahlung flux (see Figure 3).
3.3. Al Emission and ISM Metallicity
The emission line of He-like Al at ∼1.6 keV has clearly been detected. This is the first detection of this element in the X-ray spectrum of an extended celestial source. Although we looked at spectra from several smaller regions of the SNR, no spatial concentration of this emission was found. We also carefully repeated the analysis with different background regions and confirmed that the spectral feature is not due to inaccurate background subtraction. Note that the intensity of neutral Al emission in the intrinsic background of the XIS is extremely low and stable compared with XMM-Newton/EPIC (Yamaguchi et al. 2006). We emphasize that this capability has enabled us to detect this emission robustly. Chandra/ACIS has a similarly low background level, but the effective area around this energy is about a factor of two smaller than that of the XIS. The energy resolution is also lower in the ACIS, which makes detection of weak emission more difficult.
Since Al emission-line data are not available in the vnei code in XSPEC, we refer to AtomDB8 and calculate the emissivity for the He-like Al-K blend to estimate the Al abundance, AAl. The relation between the line flux FHe-like and emissivity for He-like Al is given as
where (nAl/nH)☉ is the number ratio of Al to H in the solar (Anders & Grevesse 1989). For the NEI plasma with the best-fit kTe and net values for Models Ax and Bx (Table 1), we obtain ε = 1.4 × 10−11 cm3 s−1 and 1.3 × 10−11 cm3 s−1, respectively. Therefore, the flux of the 1.6 keV Gaussian corresponds to an Al abundance of 1.3+0.4−0.3 solar for Model Ax and 1.8+0.8−0.6 solar for Model Bx, slightly higher than the solar value. Since a Type Ia SN scarcely produces Al (Iwamoto et al. 1999), this abundance enhancement indicates either (1) the ambient ISM has been enriched with Al by preceding CC SNe, or (2) the SNR really has a CC origin against our argument in Section 3.2. We consider the former is the case as we discuss below.
It has been suggested that chemical yields of 27Al and other neutron-rich elements in CC SNe strongly depend on the metallicity of progenitor stars (e.g., Kobayashi et al. 2006). This is because these elements are enhanced upon SN explosive nucleosynthesis by excess neutrons in 22Ne, which is transformed from 14N during the He-burning phase of the progenitor (see Chapter 9 of Arnett 1996). Since both Mg and Al arise from C/Ne burning, the Al-to-Mg abundance ratio can be used to indicate the metallicity. In fact, a strong metallicity dependence of the Al/Mg ratio has been confirmed by several stellar observations (Gehren et al. 2004, 2006; Andrievsky et al. 2010, and references therein). Notably, most stars with a sub-solar Mg abundance (Mg/H = 0.5–1 solar) exhibit enhanced Al/Mg values of 1–2 solar (see Figure 9 of Andrievsky et al. 2010 9), suggesting that the Al abundance in the Sun is anomalously low (and/or the Mg abundance is high) compared with nearby Galactic stars. In metal-poor stars (Mg/H < 0.1 solar), on the other hand, the Al/Mg ratio is depleted to less than 0.3 solar.
Figure 5 shows confidence contours for the abundance of Al relative to that of Mg. We obtain the Al/Mg abundance ratios of 2.5+1.5−1.0 solar and 2.1+1.1−0.7 solar for Models Ax and Bx, respectively. The ratios are, furthermore, found to be higher than unity at >99% confidence in both cases and even more significant in the case of Models As and Bs. To estimate systematic uncertainties, we fitted the spectra with the same plasma models but replaced the wabs component with an updated absorption model of Wilms et al. (2000; tbabs) where photon extinction by interstellar dust grains is additionally taken into account. We found that this change did not affect significantly the measurement of the Al/Mg ratio. We also repeated the spectral fitting by assuming different Fe abundances in the "NEI plasma" component (which can be regarded as an Fe abundance in the ISM), and obtained no significant difference in the result. The enhanced relative abundance of Al/Mg as well as the slightly depleted value of the absolute Mg abundance are consistent with the chemical characteristics in the typical Galactic stars. Therefore, we propose that the Mg and Al emission from G344.1–0.7 originates predominantly from the blast-shocked ISM with the metallicity of a solar-like value (not less than 0.1 solar). The moderate metallicity of the ambient ISM can be due to preceding CC SNe in nearby regions. However, there is still a large difficulty in the abundance measurement of Al due to the limited energy resolution (see Section 3.5), and thus future efforts are essential for more definitive conclusion.
Figure 5. Confidence contours at 68% (thin lines), 90% (thick lines), and 99% (thin dotted lines) for the abundance ratio of Al to Mg. The solar abundance ratio is shown by the dashed lines.
Download figure:
Standard image High-resolution image3.4. Cr and Mn Emissions and Progenitor's Metallicity
We have also found possible evidence of Cr and Mn emission. The centroids of these lines are fully consistent with those observed in Tycho's SNR (Tamagawa et al. 2009). We should note, however, that there are many sources of systematic uncertainties that we have not yet taken into account. For instance, we simply assume a single-temperature plasma for the NEI plasma component. The value of kTe is, therefore, determined mainly by the Kβ/Kα intensity ratios of Si and S, since these lines have a large number of photon statistics. If we allow multiple temperatures, which can be the case for most evolved SNRs, the continuum level increases slightly around the Cr and Mn features. This results in slightly lower fluxes for the weak line components; for example, adding another NEI plasma with a different electron temperature to Model Bx or Bs, we obtained a ∼20% lower flux of the Cr-Kα emission. Therefore, the detection of these features is still marginal, and we absolutely need deeper and higher energy-resolution observations to confirm their presence.
Nevertheless, it would be meaningful to make a rough estimate of the mass ratio of Mn to Cr, because this ratio is suggested to be a good metallicity tracer for Type Ia progenitors (Badenes et al. 2008) for reasons similar to those mentioned above. The progenitor's metallicity should not necessarily be consistent with that of the swept-up ISM (i.e., the source of Mg and Al), since the ISM metallicity is likely to have been modified by recent CC SNe after the Type Ia progenitor had been created. Using the best-fit values of Model Bx (Table 1), we derive the Mn/Cr flux ratio to be 0.67+0.55−0.48. Given that the ionization states of both the elements are lower than He-like, similar to Fe, the Cr and Mn ions are likely to be associated with the Fe-rich plasma. Thus, the electron temperature and ionization timescale should be in the ranges of 2–10 keV and (6–12) × 109 cm−3 s, respectively. According to Figure 4 of Badenes et al. (2008), the emissivity ratio of εMn/εCr is estimated to be 0.5–0.75. Therefore, the Mn-to-Cr mass ratio is constrained in the range of 0.1–1.0. Since the relation between the mass ratio and progenitor's metallicity is given as MMn/MCr = 5.3 × Z0.65 (Badenes et al. 2008), we obtain Z = 0.002–0.07. Although the uncertainty is relatively large, this does not conflict with the single-degenerate scenario as a candidate for the Type Ia progenitor system, where the metallicity must be higher than Z ∼ 0.001 for the "optically thick wind" to be driven effectively (Kato & Hachisu 1994; Hachisu et al. 1996; Kobayashi et al. 1998).
3.5. Future Prospect
Finally, we briefly mention the remaining problems and prospect for future observations. Although we have detected the possible feature of Al emission, our abundance estimates is still inconclusive. With the energy resolution of semiconductor detectors (e.g., the XIS), the He-like Al-Kα line is totally blended with the Mg-Kβ line, and both of them as well as the Mg-Kα line are blended with Fe L-shell emissions. Since the L-shell emissivities are generally uncertain due to the limitation of atomic data, determination of the Mg and Al abundances can be systematically affected. Interstellar dust scattering of X-ray photons out of the line of sight (e.g., Draine 2003) and abundance inhomogeneity in the foreground ISM, which were not taken into account in this paper, are potential additional sources of the uncertainties. Moreover, nonuniform temperatures and ionization timescales, expected in evolved SNRs such as G344.7–0.1, also complicate the abundance measurement.
In 2014, ASTRO-H (Takahashi et al. 2010) will be launched and will carry a micro-calorimeter (Soft X-ray Spectrometer: SXS) with greater spectral resolution for diffuse objects than has been available with previous instruments. This will enable us to resolve the K-shell lines of Mg and Al from the Fe L-shell lines and to measure the abundances much more accurately. In Figure 6, we show examples of simulated spectra for the brightest part of G344.7–0.1. The full width at half-maxima (FWHMs) are assumed to be 7 eV and 4 eV, which are the "requirement" and "goal" designs for the SXS, respectively (Mitsuda et al. 2010). In the case that the latter resolution is achieved, the fluxes of the Al-Kα and Mg-Kβ lines can be determined almost independently. We can also expect that emission from low-abundance elements, such as Al, will be observed in a large number of other SNRs. Diagnostics using such weak lines will provide us fruitful information about detailed nature of SNRs' progenitor, environment, and SN explosion mechanism.
Figure 6. Simulated ASTRO-H/SXS spectra for G344.7–0.1 with the total exposure of 300 ks, in the energies around the Al-Kα lines. The FWHM of 7 eV (top) or 4 eV (bottom) is assumed. Resonance (w), intercombination (x+y), and forbidden (z) lines of Al, and He-like Mg-Kβ line are clearly separated in the bottom.
Download figure:
Standard image High-resolution imageThe authors appreciate a number of constructive suggestions from the anonymous referee. We are also grateful to Drs. Laura A. Lopez and Kazimierz J. Borkowski for helpful discussions and Dr. Yoh Takei for providing information about ASTRO-H/SXS. H.Y. is supported by Japan Society for the Promotion of Science (JSPS) Research Fellowship for Research Abroad, and acknowledges funding from NASA ADP grant NNX09AC71G.
Footnotes
- 5
- 6
This model is based on the ion balance and emissivity calculations by Astrophysical Plasma Emission Code (APEC; Smith et al. 2001), but emission caused by inner-shell ionization and excitation is included as well. Detailed information is found at http://space.mit.edu/home/dd/Borkowski/APEC_nei_README.txt.
- 7
- 8
- 9