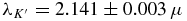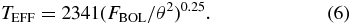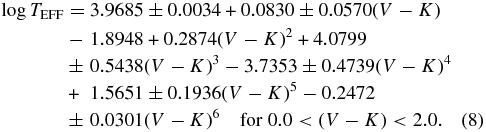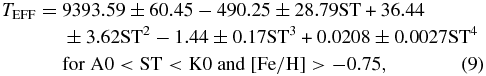ABSTRACT
We have executed a survey of nearby, main-sequence A-, F-, and G-type stars with the CHARA Array, successfully measuring the angular diameters of forty-four stars with an average precision of ∼1.5%. We present new measures of the bolometric flux, which in turn leads to an empirical determination of the effective temperature for the stars observed. In addition, these CHARA-determined temperatures, radii, and luminosities are fit to Yonsei–Yale model isochrones to constrain the masses and ages of the stars. These results are compared to indirect estimates of these quantities obtained by collecting photometry of the stars and applying them to model atmospheres and evolutionary isochrones. We find that for most cases, the models overestimate the effective temperature by ∼1.5%–4% when compared to our directly measured values. The overestimated temperatures and underestimated radii in these works appear to cause an additional offset in the star's surface gravity measurements, which consequently yield higher masses and younger ages, in particular for stars with masses greater than ∼1.3 M☉. Additionally, we compare our measurements to a large sample of eclipsing binary stars, and excellent agreement is seen within both data sets. Finally, we present temperature relations with respect to (B − V) and (V − K) colors as well as spectral type, showing that calibration of effective temperatures with errors ∼1% is now possible from interferometric angular diameters of stars.
1. INTRODUCTION
The direct measurement of the stellar angular diameter is a valuable key in determining fundamental properties of a star, particularly the linear radius and effective temperature. These properties of a star provide the link between the theory of stellar structure and evolution to model atmospheres. For nearby, main-sequence stars, where we know their distances well, the angular diameters are difficult to measure due to their tiny sizes compared to their evolved counterparts. The high angular resolution obtained through long-baseline optical/infrared interferometry has enabled us to resolve the photospheric disks of such nearby stars.
Several decades ago, a survey carried out at the Narrabri Stellar Intensity Interferometer (NSII; Hanbury Brown et al. 1974a; Code et al. 1976) was conducted to measure the angular diameters of 32 stars. This survey extended from O- to F-type stars, 11 of which were roughly on the main sequence (luminosity class V or IV).7 For several decades, luminosity class I, II, and III stars were observed with interferometers such as the Mark III and the Palomar Testbed Interferometer, but no main-sequence star earlier than A7 was measured (Davis 1997).
As an update, the CHARM2 Catalogue (Richichi et al. 2005) provides a compilation of stellar diameters by means of direct measurements by high angular resolution methods, as well as indirect estimates. The CHARM2 Catalogue includes all results as of 2004 July, a total of 8231 entries. Filtering out the entries to include only unique sources where direct measurements exist with errors in the angular diameter measurements of less than 5%, this number drops to 242, and only 24 of these reside on the main sequence (luminosity class V or IV).
In a recent work by Holmberg et al. (2008), they remark that measurements of the angular diameters of main-sequence F and G stars need to be better than 2%, yielding temperatures to 1%, in order for offsets in the color–temperature calibrations to be minimal. At that time, only nine stars met this criterion. This precision limit reiterates the target accuracy proposed by Blackwell et al. (1979) for the limits to the Infrared Flux Method that a good TEFF determination goal should be 1% to match the best atomic data available for abundance determinations and log g estimates (Davis 1985; Booth 1997).
The long baselines of the CHARA Array are uniquely suited for observing diameters of main-sequence stars to great precision. In this paper, we present the angular diameters of 44 main-sequence A-, F-, and G-type stars measured with the CHARA Array, the most extensive interferometric survey of main-sequence stars to date. Details on the observing strategy and observations are in Section 2, and the results are presented and discussed in Section 3. In Section 3, we also discuss the consistency of our results compared to the recent work of van Belle & von Braun (2009), who used the Palomar Testbed Interferometer to observe a few dozen main-sequence stars, where 14 of these stars are common sources with this work. Section 4 introduces the fundamental stellar properties of linear radii, luminosities, and effective temperatures for the stars observed. In the discussion (Section 5), we use our data to derive empirical temperature relations to (B − V) and (V − K) colors and spectral type. We also present masses and ages for the sample obtained via isochrone fitting and masses computed by combining our radii with published values of surface gravities. Our results are compared to three surveys in the literature that have a large percentage of stars in common with our survey, as well as a large sample of non-interacting eclipsing binaries. We summarize in Section 6.
2. OBSERVATIONS WITH THE CHARA ARRAY
2.1. Instrument
The CHARA Array is an optical/infrared interferometric array located at Mount Wilson Observatory in the San Gabriel mountains of southern California (a detailed description of the instrument can be found in ten Brummelaar et al. 2005). Briefly, the CHARA Array consists of six, 1 m aperture telescopes in a Y-shaped configuration spread across the mountaintop of the Observatory. With the six telescopes, there are 15 available baseline combinations, ranging from 34 to 331 m, at a variety of position angle orientations ψ. The CHARA Array currently is the longest baseline operational optical/infrared interferometer in the world.
There are several beam combiners available for the CHARA Array, and for this project, the observations were made using the CHARA Classic beam combiner in two-telescope mode. CHARA Classic is a pupil-plane beam combiner, which is used in the K' band, empirically measured in Bowsher et al. (2010) to have a central wavelength of m. Fringes are detected and recorded on the Near Infrared Observer (NIRO) camera, which is based upon an HgCdTe PICNIC Array readout at high speed. Nearly all (98.5%) of the observing for this work was performed remotely from Georgia State University's Cleon Arrington Remote Operations Center (AROC) in Atlanta, GA during the 2007, 2008, and 2009 observing seasons.
2.2. Target Selection
The main goal of this survey is to determine the angular diameters of a large number of stars to high precision. We limited the stars observed by selecting only those for which the predicted precision of the measured angular diameter will be better than 4%. The precision of a measurement of the stellar angular diameter depends on how far down the visibility curve one is able to sample. The expression of the uniform disk visibility function of a single star (Equation (1)) is dependent on B the projected baseline, θ the angular diameter of the star, and λ the wavelength of observation:
where
and J1 is the first-order Bessel function. By knowing the λ and B utilized in a given observation, we can estimate the optimum resolution range resulting from the precision with which we can measure the object visibility. To ensure that we reach the precision goal of σθ < 4% for our observations, we find the approximate limiting resolution is θ ∼ 0.65 mas for K'. In reality, this number will vary (for example, see Baines et al. 2008), but its use to establish a first-order cutoff for a preliminary sample selection is appropriate.
Each star we chose to observe was then hand selected from a Hipparcos catalog query. This process was initiated from assumptions of the nominal linear size of a main-sequence star from Cox (2000) based on B − V colors, in order to determine a maximum distance to be sampled for each spectral type before reaching the θ = 0.65 mas resolution limit. Additionally, the luminosity class of the star was restricted by apparent V magnitudes to only admit roughly main-sequence stars (Cox 2000). The declination limit to this survey was restricted to targets above −10° declination. All stars were easily within the magnitude limits for observing with the CHARA Array, with magnitudes ranging from 2.5 < V < 6.4 and 1.6 < K < 4.4.8 Table 1 lists the names, coordinates, spectral types, magnitudes, metallicity [Fe/H], and Hipparcos distance of the stars observed.
Table 1. Target Sample of A, F, and G Dwarfs
| HD | HR | HIP | Other | R.A. | Decl. | Spectral | Spectral | V | K | (B − V) | [Fe/H]d | π ± σe |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Namea | (hh mm ss.xx) | (dd mm ss) | Typeb | Typec | (mag) | (mag) | (mag) | (mas) | ||||
| 4614 | 219 | 3821 | 24 η Cas A | 00 49 06.29 | 57 48 54.67 | F9V | G0V | 3.46 | 2.05 | 0.587 | −0.30 | 168.01 ± 0.48 |
| 5015 | 244 | 4151 | GJ 41 | 00 53 04.20 | 61 07 26.29 | F8V | F8V | 4.80 | 3.54 | 0.540 | 0.00 | 53.35 ± 0.33 |
| 6582 | 321 | 5336 | 34 μ Cas A | 01 08 16.39 | 54 55 13.22 | G5Vb | G5Vp | 5.17 | 3.36 | 0.704 | −0.83 | 132.40 ± 0.60 |
| 10780 | 511 | 8362 | GJ 75 | 01 47 44.84 | 63 51 09.00 | G9V | K0V | 5.63 | 3.84 | 0.804 | 0.05 | 99.34 ± 0.53 |
| 16895 | 799 | 12777 | 13 θ Per A | 02 44 11.99 | 49 13 42.41 | F7V | F7V | 4.10 | 2.78 | 0.514 | −0.12 | 89.88 ± 0.23 |
| 19373 | 937 | 14632 | ι Per | 03 09 04.02 | 49 36 47.80 | G0IV-V | G0V | 4.05 | 2.70 | 0.595 | 0.09 | 94.87 ± 0.23 |
| 20630 | 996 | 15457 | κ Cet | 03 19 21.70 | 03 22 12.71 | G5V | G5Vvar | 4.84 | 3.34 | 0.681 | 0.00 | 109.39 ± 0.27 |
| 22484 | 1101 | 16852 | 10 Tau | 03 36 52.38 | 00 24 05.98 | F9IV-V | F9V | 4.29 | 2.93 | 0.575 | −0.09 | 71.60 ± 0.54 |
| 30652 | 1543 | 22449 | 1 π3 Ori | 04 49 50.41 | 06 57 40.59 | F6IV-V | F6V | 3.19 | 2.07 | 0.484 | −0.03 | 123.94 ± 0.17 |
| 34411 | 1729 | 24813 | 15 λ Aur | 05 19 08.47 | 40 05 56.59 | G1V | G0V | 4.69 | 3.24 | 0.630 | 0.05 | 79.18 ± 0.28 |
| 39587 | 2047 | 27913 | 54 χ1 Ori | 05 54 22.98 | 20 16 34.23 | G0IV-V | G0V | 4.39 | 2.97 | 0.594 | −0.16 | 115.42 ± 0.27 |
| 48737 | 2484 | 32362 | 31 ξ Gem | 06 45 17.37 | 12 53 44.13 | F5IV-V | F5IV | 3.35 | 2.30 | 0.443 | 0.01 | 55.55 ± 0.19 |
| 56537 | 2763 | 35350 | 54 λ Gem | 07 18 05.58 | 16 32 25.38 | ⋅⋅⋅ | A3V | 3.58 | 3.27 | 0.106 | ⋅⋅⋅ | 32.36 ± 0.22 |
| 58946 | 2852 | 36366 | 62 ρ Gem | 07 29 06.72 | 31 47 04.38 | ⋅⋅⋅ | F0V | 4.16 | 3.32 | 0.320 | −0.31 | 55.41 ± 0.25 |
| 81937 | 3757 | 46733 | 23 h UMa | 09 31 31.71 | 63 03 42.70 | ⋅⋅⋅ | F0IV | 3.65 | 2.82 | 0.360 | 0.06 | 41.99 ± 0.16 |
| 82328 | 3775 | 46853 | 25 θ UMa | 09 32 51.43 | 51 40 38.28 | F5.5IV-V | F6IV | 3.17 | 2.02 | 0.475 | −0.12 | 74.18 ± 0.13 |
| 82885 | 3815 | 47080 | 11 LMi | 09 35 39.50 | 35 48 36.48 | G8+V | G8IV-V | 5.40 | 3.70 | 0.770 | 0.06 | 87.96 ± 0.32 |
| 86728 | 3951 | 49081 | 20 LMi | 10 01 00.66 | 31 55 25.22 | G4V | G3V | 5.37 | 3.82 | 0.676 | 0.20 | 66.47 ± 0.32 |
| 90839 | 4112 | 51459 | 36 UMa | 10 30 37.58 | 55 58 49.93 | F8V | F8V | 4.82 | 3.54 | 0.541 | −0.16 | 78.26 ± 0.29 |
| 95418 | 4295 | 53910 | 48 β UMa | 11 01 50.48 | 56 22 56.74 | A1IV | A1V | 2.34 | 2.35 | 0.033 | 0.06 | 40.89 ± 0.16 |
| 97603 | 4357 | 54872 | 68 δ Leo | 11 14 06.50 | 20 31 25.38 | A5IV(n) | A4V | 2.56 | 2.26 | 0.128 | 0.00 | 55.82 ± 0.25 |
| 101501 | 4496 | 56997 | 61 UMa | 11 41 03.02 | 34 12 05.89 | G8V | G8V | 5.31 | 3.53 | 0.723 | −0.12 | 104.03 ± 0.26 |
| 102870 | 4540 | 57757 | 5 β Vir | 11 50 41.72 | 01 45 52.98 | F8.5IV-V | F8V | 3.59 | 2.33 | 0.518 | 0.11 | 91.50 ± 0.22 |
| 103095 | 4550 | 57939 | CF UMa | 11 52 58.77 | 37 43 07.24 | K1V | G8Vp | 6.42 | 4.38 | 0.754 | −1.36 | 109.98 ± 0.41 |
| 109358 | 4785 | 61317 | 8 β CVn | 12 33 44.55 | 41 21 26.93 | G0V | G0V | 4.24 | 2.72 | 0.588 | −0.30 | 118.49 ± 0.20 |
| 114710 | 4983 | 64394 | 43 β Com | 13 11 52.39 | 27 52 41.46 | G0V | G0V | 4.23 | 2.90 | 0.572 | −0.06 | 109.53 ± 0.17 |
| 118098 | 5107 | 66249 | 79 ζ Vir | 13 34 41.59 | −00 35 44.95 | A2Van | A3V | 3.38 | 3.11 | 0.114 | −0.02 | 44.01 ± 0.19 |
| 126660 | 5404 | 70497 | 23 θ Boo | 14 25 11.80 | 51 51 02.68 | F7V | F7V | 4.04 | 2.78 | 0.497 | −0.14 | 68.83 ± 0.14 |
| 128167 | 5447 | 71284 | 28 σ Boo | 14 34 40.82 | 29 44 42.47 | F4VkF2mF1 | F3V | 4.47 | 3.52 | 0.364 | −0.36 | 63.16 ± 0.26 |
| 131156 | 5544 | 72659 | 37 ξ Boo | 14 51 23.38 | 19 06 01.66 | G7V | G8V | 4.54 | 2.96 | 0.720 | −0.33 | 149.03 ± 0.48 |
| 141795 | 5892 | 77622 | 37  Ser Ser |
15 50 48.97 | 04 28 39.83 | kA2hA5mA7V | A2m | 3.71 | 3.43 | 0.147 | ⋅⋅⋅ | 46.28 ± 0.19 |
| 142860 | 5933 | 78072 | 41 γ Ser | 15 56 27.18 | 15 39 41.82 | F6V | F6V | 3.85 | 2.66 | 0.478 | −0.19 | 88.85 ± 0.18 |
| 146233 | 6060 | 79672 | 18 Sco | 16 15 37.27 | −08 22 09.99 | G2V | G1V | 5.49 | 3.55 | 0.652 | −0.02 | 71.93 ± 0.37 |
| 162003 | 6636 | 86614 | 31 ψ Dra | 17 41 56.36 | 72 08 55.84 | F5IV-V | F5IV-V | 4.57 | 3.43 | 0.434 | −0.17 | 43.79 ± 0.45 |
| 164259 | 6710 | 88175 | 57 ζ Ser | 18 00 29.01 | −03 41 24.97 | F2V | F3V | 4.62 | 3.66 | 0.390 | −0.14 | 42.44 ± 0.33 |
| 173667 | 7061 | 92043 | 110 Her | 18 45 39.73 | 20 32 46.71 | F5.5IV-V | F6V | 4.19 | 2.89 | 0.483 | −0.15 | 52.06 ± 0.24 |
| 177724 | 7235 | 93747 | 17 ζ Aql | 19 05 24.61 | 13 51 48.52 | A0IV-Vnn | A0Vn | 2.99 | 2.92 | 0.014 | −0.68 | 39.27 ± 0.17 |
| 182572 | 7373 | 95447 | 31 b Aql | 19 24 58.20 | 11 56 39.90 | ⋅⋅⋅ | G8IV | 5.17 | 3.53 | 0.761 | 0.33 | 65.89 ± 0.26 |
| 185144 | 7462 | 96100 | 61 σ Dra | 19 32 21.59 | 69 39 40.23 | G9V | K0V | 4.67 | 2.78 | 0.786 | −0.24 | 173.77 ± 0.18 |
| 185395 | 7469 | 96441 | 13 θ Cyg | 19 36 26.54 | 50 13 15.97 | F3+V | F4V | 4.49 | 3.52 | 0.395 | −0.04 | 54.55 ± 0.15 |
| 210418 | 8450 | 109427 | 26 θ Peg | 22 10 11.99 | 06 11 52.31 | ⋅⋅⋅ | A2V | 3.52 | 3.22 | 0.086 | −0.38 | 35.34 ± 0.85 |
| 213558 | 8585 | 111169 | 7 α Lac | 22 31 17.50 | 50 16 56.97 | ⋅⋅⋅ | A1V | 3.76 | 3.75 | 0.031 | ⋅⋅⋅ | 31.80 ± 0.12 |
| 215648 | 8665 | 112447 | 46 ξ Peg | 22 46 41.58 | 12 10 22.40 | F6V | F7V | 4.20 | 2.87 | 0.502 | −0.24 | 61.37 ± 0.20 |
| 222368 | 8969 | 116771 | 17 ι Psc | 23 39 57.04 | 05 37 34.65 | F7V | F7V | 4.13 | 2.89 | 0.507 | −0.08 | 72.91 ± 0.15 |
Notes. aBayer-Flamsteed or GJ (Kostjuk 2004). bGray et al. (2001, 2003). cSIMBAD (Wenger et al. 2000). dHolmberg et al. (2007), when available. For stars without metallicity estimates from Holmberg et al. (2007), the [M/H] values from Gray et al. (2003, 2006; HD 82885, HD 97603, HD 118098, HD 131156, HD 177724, HD 210418), and Takeda et al. (2005; HD 182572) are used. Stars with no metallicity measurements are HD 56537, HD 141795, and HD 213558. evan Leeuwen (2007).
Download table as: ASCIITypeset image
2.3. Data Calibration
We follow the standard routine for interferometric observing where a calibrator star with known size is observed before and after every observation of a science object,9 which enables us to remove the instrumental response of the system as well as effects from local seeing conditions. A description of the ideal calibrator and the propagation of errors to the true visibility measurements of the science star can be found in van Belle & van Belle (2005). The calibrator stars used in this work were initially selected from the getCal web interface10 and were restricted by angular distance in the sky to the object, magnitude, and its estimated angular size. In most cases, the calibrator star was less than 6° from the object, and never lying further than ∼10°. The closeness of the object to the calibrator is crucial for quickly acquiring brackets, where under typical observing conditions, there is approximately 4–5 minutes between observations. The magnitudes of the calibrator stars were chosen from observability limits with our telescopes and instrument. Finally, the estimated angular size of the calibrator was the attribute that is most weighted in the calibrator searching process.
With CHARA's long baselines, unwanted biases may be introduced if the calibrator is resolved. If possible, calibrators were chosen to have a angular diameter less than 0.45 mas, following the example described in van Belle & van Belle (2005) for CHARA's maximum baseline of 331 m. In order to estimate the calibrator's angular size, θSED, a Kurucz model spectral energy distribution (SED) was fit to Johnson UBV (Mermilliod 1997), Strömgren uvby (Hauck & Mermilliod 1998), and Two Micron All Sky Survey (2MASS) JHK (Cutri et al. 2003) flux-calibrated photometry.11 The calibrators used in this work are listed in Table 2. Table 2 also shows the calibrator Johnson, Strömgren, and 2MASS magnitudes, and θSED fit for each star. The last column lists the science object(s) observed with that calibrator.
Table 2. Calibrators Observed
| Calibrator | V | B − V | U − B | v | b − y | m1 | c1 | J | H | K | θSED ± σ | Target (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HD | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | (mag) | (mas) | HD |
| 71 | 6.990 | 1.187 | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | 5.193 | 4.459 | 4.214 | 0.682 ± 0.024 | 4614 |
| 6210 | 5.838 | 0.547 | 0.110 | 5.800 | 0.356 | 0.183 | 0.475 | 4.755 | 4.794 | 4.445 | 0.519 ± 0.012 | 4614, 5015, 6582, 10780 |
| 9407 | 6.530 | 0.684 | 0.236 | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | 5.296 | 4.941 | 4.888 | 0.430 ± 0.017 | 4614 |
| 20675 | 5.932 | 0.441 | −0.015 | 5.950 | 0.293 | 0.167 | 0.495 | 5.274 | 4.922 | 4.875 | 0.415 ± 0.012 | 16895, 19373 |
| 21790 | 4.727 | −0.093 | −0.260 | 4.738 | −0.036 | 0.107 | 0.833 | 5.282 | 4.960 | 4.886 | 0.308 ± 0.009 | 20630, 22484 |
| 22879 | 6.689 | 0.540 | −0.086 | 6.693 | 0.365 | 0.126 | 0.272 | 5.588 | 5.301 | 5.179 | 0.342 ± 0.021 | 20630, 22484 |
| 28355 | 5.025 | 0.218 | 0.120 | 5.023 | 0.115 | 0.225 | 0.909 | 4.793 | 4.656 | 4.534 | 0.425 ± 0.030 | 30652 |
| 30739 | 4.355 | 0.009 | −0.016 | 4.370 | 0.010 | 0.153 | 1.107 | 3.825 | 4.208 | 4.166 | 0.461 ± 0.018 | 30652 |
| 31295 | 4.644 | 0.085 | 0.095 | 4.661 | 0.044 | 0.178 | 1.007 | 4.846 | 4.517 | 4.416 | 0.439 ± 0.043 | 30652 |
| 34904 | 5.540 | 0.120 | 0.120 | 5.540 | 0.084 | 0.163 | 1.101 | 5.144 | 5.124 | 5.112 | 0.345 ± 0.013 | 34411 |
| 38558 | 5.527 | 0.274 | 0.249 | 5.400 | 0.196 | 0.148 | 1.176 | 4.944 | 4.746 | 4.483 | 0.422 ± 0.008 | 39587 |
| 42807 | 6.442 | 0.660 | 0.160 | 6.440 | 0.415 | 0.228 | 0.292 | 5.253 | 5.010 | 4.849 | 0.429 ± 0.016 | 48737 |
| 43042 | 5.201 | 0.434 | −0.011 | 5.207 | 0.291 | 0.166 | 0.443 | 4.008 | 3.827 | 4.129 | 0.591 ± 0.030 | 39587 |
| 43795 | 7.640 | 0.958 | ⋅⋅⋅ | 7.645 | 0.593 | 0.293 | 0.483 | 5.940 | 5.522 | 5.409 | 0.376 ± 0.008 | 48682 |
| 50277 | 5.765 | 0.265 | 0.089 | 5.764 | 0.154 | 0.184 | 0.872 | 5.308 | 5.232 | 5.088 | 0.346 ± 0.011 | 48737 |
| 50973 | 4.897 | 0.029 | 0.053 | 4.917 | 0.013 | 0.159 | 1.107 | 5.055 | 4.941 | 4.793 | 0.361 ± 0.026 | 48682 |
| 58551 | 6.544 | 0.460 | 0.000 | 6.539 | 0.322 | 0.129 | 0.355 | 5.534 | 5.380 | 5.245 | 0.357 ± 0.009 | 56537 |
| 59037 | 5.011 | 0.112 | 0.119 | 5.084 | 0.063 | 0.201 | 1.015 | 4.818 | 4.793 | 4.744 | 0.389 ± 0.018 | 58946 |
| 65583 | 6.999 | 0.713 | 0.181 | 6.975 | 0.450 | 0.232 | 0.231 | 5.539 | 5.170 | 5.095 | 0.406 ± 0.033 | 58946 |
| 79439 | 4.832 | 0.186 | 0.087 | 0.113 | 0.196 | 0.892 | 2.833 | 4.481 | 4.353 | 4.291 | 0.482 ± 0.035 | 82328 |
| 80290 | 6.160 | 0.420 | −0.110 | 6.132 | 0.300 | 0.139 | 0.392 | 5.219 | 5.067 | 4.972 | 0.385 ± 0.016 | 82328 |
| 83951 | 6.140 | 0.360 | 0.000 | 6.000 | 0.244 | 0.162 | 0.594 | 5.355 | 5.246 | 5.169 | 0.360 ± 0.006 | 82885, 86728 |
| 87141 | 5.749 | 0.476 | 0.043 | 5.700 | 0.318 | 0.169 | 0.478 | 4.987 | 4.730 | 4.503 | 0.476 ± 0.022 | 81937, 82328, 95418 |
| 88986 | 6.460 | 0.600 | 0.160 | 6.440 | 0.397 | 0.209 | 0.363 | 5.247 | 4.946 | 4.884 | 0.432 ± 0.013 | 82885, 86728 |
| 89389 | 6.450 | 0.540 | 0.080 | 0.369 | 0.181 | 0.370 | 2.602 | 5.340 | 5.091 | 5.020 | 0.398 ± 0.013 | 81937, 82328, 90839, 95418 |
| 91480 | 5.159 | 0.335 | −0.020 | 5.140 | 0.228 | 0.159 | 0.574 | 4.922 | 4.688 | 4.334 | 0.518 ± 0.014 | 81937, 90839, 95418 |
| 99285 | 5.610 | 0.345 | −0.017 | 5.640 | 0.251 | 0.154 | 0.595 | 4.815 | 4.723 | 4.624 | 0.456 ± 0.017 | 97603 |
| 99984 | 5.964 | 0.493 | −0.025 | 5.800 | 0.340 | 0.148 | 0.429 | 4.900 | 4.657 | 4.591 | 0.483 ± 0.020 | 103095 |
| 102124 | 4.838 | 0.176 | 0.091 | 4.858 | 0.090 | 0.196 | 0.926 | 4.634 | 4.542 | 4.409 | 0.466 ± 0.022 | 102870 |
| 102634 | 6.145 | 0.520 | 0.069 | 6.153 | 0.329 | 0.176 | 0.439 | 5.212 | 5.081 | 4.921 | 0.404 ± 0.010 | 102870 |
| 103799 | 6.622 | 0.469 | −0.026 | 0.326 | 0.139 | 0.422 | 2.618 | 5.594 | 5.386 | 5.338 | 0.343 ± 0.013 | 101501, 103095, 109358 |
| 110897 | 5.956 | 0.548 | −0.044 | 5.958 | 0.374 | 0.147 | 0.284 | 5.173 | 4.667 | 4.465 | 0.492 ± 0.022 | 109358 |
| 114093 | 6.830 | 0.910 | 0.000 | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | 5.115 | 4.739 | 4.564 | 0.572 ± 0.014 | 114710 |
| 116831 | 5.956 | 0.187 | 0.125 | 5.973 | 0.095 | 0.206 | 0.972 | 5.668 | 5.577 | 5.531 | 0.278 ± 0.020 | 118098 |
| 120066 | 6.329 | 0.621 | 0.151 | 6.329 | 0.399 | 0.188 | 0.397 | 5.212 | 4.997 | 4.851 | 0.428 ± 0.013 | 118098 |
| 128093 | 6.332 | 0.397 | −0.022 | 6.200 | 0.300 | 0.131 | 0.476 | 5.460 | 5.287 | 5.222 | 0.351 ± 0.011 | 128167 |
| 129153 | 5.915 | 0.218 | 0.045 | 0.131 | 0.206 | 0.813 | 2.816 | 5.447 | 5.402 | 5.365 | 0.309 ± 0.010 | 131156 |
| 132254 | 5.639 | 0.496 | −0.003 | 5.600 | 0.338 | 0.174 | 0.410 | 4.685 | 4.464 | 4.408 | 0.520 ± 0.015 | 126660 |
| 135101 | 6.689 | 0.680 | 0.260 | 6.685 | 0.433 | 0.220 | 0.368 | 5.403 | 5.090 | 5.030 | 0.409 ± 0.014 | 131156 |
| 139225 | 5.950 | 0.280 | 0.020 | 5.800 | 0.222 | 0.160 | 0.681 | 5.175 | 5.099 | 5.023 | 0.380 ± 0.122 | 142860 |
| 140775 | 5.571 | 0.035 | 0.059 | 5.568 | 0.024 | 0.150 | 1.107 | 5.466 | 5.463 | 5.428 | 0.275 ± 0.013 | 141795 |
| 145607 | 5.420 | 0.120 | 0.120 | 5.443 | 0.059 | 0.172 | 1.083 | 5.170 | 5.307 | 5.052 | 0.325 ± 0.020 | 146233 |
| 150177 | 6.390 | 0.490 | −0.100 | 6.333 | 0.334 | 0.119 | 0.395 | 5.353 | 5.064 | 4.977 | 0.391 ± 0.019 | 146233 |
| 154099 | 6.300 | 0.240 | 0.110 | 6.308 | 0.158 | 0.180 | 0.944 | 5.706 | 5.633 | 5.604 | 0.283 ± 0.005 | 162003 |
| 158352 | 5.418 | 0.227 | 0.094 | 5.420 | 0.148 | 0.183 | 0.923 | 4.813 | 4.883 | 4.805 | 0.407 ± 0.013 | 164259 |
| 162004 | 5.808 | 0.531 | 0.032 | 5.780 | 0.346 | 0.160 | 0.379 | 5.001 | 4.590 | 4.527 | 0.498 ± 0.015 | 162003 |
| 167564 | 6.350 | 0.200 | 0.150 | 6.354 | 0.123 | 0.158 | 1.148 | 5.891 | 5.791 | 5.750 | 0.259 ± 0.004 | 165259 |
| 174897 | 6.550 | 1.050 | 0.850 | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | ⋅⋅⋅ | 4.797 | 4.384 | 4.096 | 0.652 ± 0.038 | 182572 |
| 176303 | 5.239 | 0.530 | 0.066 | 5.267 | 0.356 | 0.168 | 0.452 | 4.324 | 4.039 | 3.930 | 0.659 ± 0.016 | 173667, 177724, 182572 |
| 180317 | 5.640 | 0.110 | 0.000 | 5.600 | 0.068 | 0.184 | 1.072 | 5.330 | 5.381 | 5.302 | 0.309 ± 0.007 | 173667, 177724 |
| 183534 | 5.750 | 0.000 | −0.020 | 5.750 | −0.003 | 0.157 | 1.023 | 5.632 | 5.690 | 5.674 | 0.241 ± 0.012 | 185395 |
| 191195 | 5.826 | 0.418 | −0.030 | 5.817 | 0.284 | 0.153 | 0.506 | 5.239 | 4.834 | 4.766 | 0.432 ± 0.014 | 185395 |
| 193664 | 5.919 | 0.585 | 0.058 | 5.922 | 0.382 | 0.180 | 0.323 | 4.879 | 4.690 | 4.451 | 0.494 ± 0.019 | 185144 |
| 204485 | 5.797 | 0.304 | 0.009 | 5.700 | 0.200 | 0.198 | 0.648 | 5.156 | 5.020 | 4.955 | 0.381 ± 0.011 | 201091, 201092 |
| 210715 | 5.393 | 0.154 | 0.069 | 5.400 | 0.076 | 0.200 | 0.967 | 5.013 | 5.016 | 4.959 | 0.366 ± 0.015 | 213558 |
| 211976 | 6.178 | 0.450 | −0.052 | 6.183 | 0.300 | 0.148 | 0.423 | 5.323 | 5.160 | 5.050 | 0.373 ± 0.013 | 210418, 215648 |
| 214923 | 3.406 | −0.086 | −0.217 | 3.406 | −0.035 | 0.113 | 0.868 | 3.538 | 3.527 | 3.566 | 0.611 ± 0.029 | 215648 |
| 216735 | 4.906 | −0.002 | 0.003 | 4.915 | −0.006 | 0.159 | 1.083 | 5.222 | 5.012 | 4.840 | 0.321 ± 0.022 | 215648, 222368 |
| 218470 | 5.680 | 0.417 | −0.039 | 5.687 | 0.290 | 0.146 | 0.486 | 4.819 | 4.670 | 4.649 | 0.462 ± 0.014 | 213558 |
| 222603 | 4.502 | 0.202 | 0.078 | 4.500 | 0.105 | 0.203 | 0.891 | 4.372 | 4.204 | 4.064 | 0.577 ± 0.032 | 222368 |
| 225003 | 5.704 | 0.329 | −0.007 | 5.699 | 0.209 | 0.155 | 0.645 | 5.077 | 5.008 | 4.910 | 0.386 ± 0.017 | 222368 |
Notes. Johnson UBV (Mermilliod 1997), Stromgren uvby (Hauck & Mermilliod 1998), and 2MASS JHK (Cutri et al. 2003) magnitudes for the calibrator stars. Refer to Section 2.3 for details.
Download table as: ASCIITypeset image
Two-thirds of the calibrators used meet the θSED < 0.45 mas criteria.12 In many cases, the science stars were observed with more than one calibrator, on more than one occasion, in order to reduce the likelihood of biases being introduced (for example, see HD 30652; Table 3). In some instances, we were not so fortunate to observe stars with multiple calibrators having the ideal angular size of θSED < 0.45 mas. For instance, the stars HD 5015, HD 6582, and HD 10780 were observed with only one calibrator, HD 6210 (θSED = 0.519 mas). However, we note that the observations of the star HD 4614 were also obtained with this calibrator as well as two additional calibrators, one of which meets the ideal criterion for being completely unresolved (HD 9407, θSED = 0.430 mas). We find that all the calibrated data sets for HD 4614 agree flawlessly in the final diameter fits. Thus, using the slightly resolved calibrator star HD 6210 is not a cause of concern. Only four stars, HD 97603, HD 185144, HD 126660, and HD 114710 have observations with only one calibrator with 0.45 mas < θSED < 0.57 mas, but consistency in the calibration process seen with stars observed with more than one calibrator (such as HD 4614) provides assurance that this issue is not a problematic one. Additionally, the maximum CHARA baseline of 331 m was never reached for a significant amount of these observations, thus pushing the theorized ideal maximum angular size for the calibrator to larger sizes.
Table 3. Observation Log
| Object | UT Date | Baseline | No. of | Calibrator |
|---|---|---|---|---|
| HD | (yyyy/mm/dd) | Brackets | HD | |
| 4614 | 2007/06/29 | W1/E1 | 2 | 6210 |
| 2007/06/30 | W1/E1 | 5 | 6210 | |
| 2007/07/01 | W1/E1 | 3 | 6210 | |
| 2007/07/18 | S1/E1 | 3 | 6210 | |
| 2007/07/19 | S1/E1 | 3 | 6210 | |
| 2007/11/16 | S1/E1 | 4 | 6210 | |
| 2008/10/02 | W1/E1 | 4 | 6210, 9407 | |
| 2009/11/21 | S1/E1 | 3 | 71 | |
| 5015 | 2007/10/10 | W1/E1 | 10 | 6210 |
| 2007/11/03 | W1/E1 | 7 | 6210 | |
| 2007/11/17 | S1/E1 | 8 | 6210 | |
| 6582 | 2007/07/01 | W1/E1 | 3 | 6210 |
| 2007/07/17 | S1/E1 | 6 | 6210 | |
| 2007/07/18 | S1/E1 | 8 | 6210 | |
| 2007/09/08 | S1/E1 | 10 | 6210 | |
| 10780 | 2007/06/29 | W1/E1 | 2 | 6210 |
| 2007/07/19 | S1/E1 | 10 | 6210 | |
| 2007/10/10 | W1/E1 | 10 | 6210 | |
| 16895 | 2007/09/08 | S1/E1 | 7 | 20675 |
| 2007/11/03 | W1/E1 | 8 | 20675 | |
| 2007/12/24 | S1/E1 | 6 | 20675 | |
| 19373 | 2007/01/25 | S1/E1 | 8 | 20675 |
| 2007/08/28 | W1/S1 | 2 | 20675 | |
| 2007/09/08 | S1/E1 | 10 | 20675 | |
| 2007/11/04 | W1/E1 | 6 | 20675 | |
| 20630 | 2007/09/09 | S1/E1 | 9 | 21790 |
| 2008/10/01 | S1/E1 | 4 | 22879 | |
| 2008/11/17 | S1/E1 | 5 | 22879 | |
| 2008/11/18 | S1/E1 | 5 | 21790, 22879 | |
| 22484 | 2006/12/05 | S1/E1 | 2 | 21790 |
| 2006/12/07 | S1/E1 | 3 | 21790 | |
| 2007/09/09 | S1/E1 | 8 | 21790 | |
| 2008/10/01 | S1/E1 | 6 | 22879 | |
| 2008/10/02 | W1/E1 | 4 | 22879 | |
| 30652 | 2007/11/05 | S1/E1 | 16 | 30739 |
| 2008/10/01 | S1/E1 | 10 | 28355, 31295 | |
| 2008/10/02 | W1/E1 | 3 | 31295 | |
| 34411 | 2007/01/26 | S1/E1 | 5 | 34904 |
| 2007/11/03 | W1/E1 | 8 | 34904 | |
| 2007/11/15 | S1/E1 | 4 | 34904 | |
| 2007/11/17 | S1/E1 | 7 | 34904 | |
| 39587 | 2006/12/07 | S1/E1 | 3 | 38558 |
| 2007/03/06 | S1/E1 | 8 | 38558 | |
| 2008/11/18 | S1/E1 | 11 | 38558, 43042 | |
| 48737 | 2006/12/07 | S1/E1 | 4 | 50277 |
| 2008/11/17 | S1/E1 | 12 | 42807, 50277 | |
| 2008/11/18 | S1/E1 | 11 | 42807, 50277 | |
| 56537 | 2007/02/21 | S1/E1 | 1 | 58551 |
| 2007/02/25 | S1/E1 | 7 | 58551 | |
| 2007/03/11 | S1/E1 | 6 | 58551 | |
| 2007/11/04 | S1/E1 | 5 | 58551 | |
| 2007/12/23 | S1/E1 | 5 | 58551 | |
| 58946 | 2007/01/25 | S1/E1 | 6 | 65583 |
| 2007/11/16 | S1/E1 | 7 | 59037 | |
| 2007/11/17 | S1/E1 | 7 | 59037 | |
| 81937 | 2007/11/29 | S2/E2 | 9 | 91480 |
| 2009/11/20 | S1/E1 | 12 | 87141, 89389, 91480 | |
| 2009/11/21 | S1/E1 | 4 | 87141 | |
| 2009/11/22 | S1/E1 | 2 | 91480 | |
| 82328 | 2007/11/02 | W2/E2 | 9 | 87141 |
| 2009/11/20 | S1/E1 | 7 | 79439, 80290, 89389 | |
| 2009/11/22 | S1/E1 | 3 | 79439 | |
| 82885 | 2007/02/03 | S1/E1 | 2 | 83951 |
| 2007/11/03 | W1/E1 | 7 | 83951 | |
| 2007/11/07 | S1/E1 | 9 | 83951 | |
| 2007/12/24 | S1/E1 | 5 | 83951 | |
| 2009/11/21 | S1/E1 | 3 | 88986 | |
| 86728 | 2007/11/15 | S1/E1 | 10 | 83951 |
| 2007/11/16 | S1/E1 | 2 | 83951 | |
| 2007/12/24 | S1/E1 | 6 | 83951 | |
| 2008/11/16 | S1/E1 | 10 | 83951, 88986 | |
| 2009/11/21 | S1/E1 | 4 | 88986 | |
| 90839 | 2007/11/16 | S1/E1 | 10 | 89389 |
| 2008/04/17 | W1/S1 | 5 | 89389, 91480 | |
| 95418 | 2007/04/04 | S1/E1 | 7 | 91480 |
| 2007/11/07 | S1/E1 | 6 | 91480 | |
| 2008/04/17 | W1/S1 | 5 | 89389, 91480 | |
| 2009/11/21 | S1/E1 | 3 | 87141 | |
| 2009/11/22 | S1/E1 | 4 | 91480 | |
| 97603 | 2007/02/21 | S1/E1 | 10 | 99285 |
| 2007/03/10 | S1/E1 | 2 | 99285 | |
| 2007/03/11 | S1/E1 | 5 | 99285 | |
| 101501 | 2007/11/15 | S1/E1 | 7 | 103799 |
| 2007/12/24 | S1/E1 | 3 | 103799 | |
| 102870 | 2007/03/09 | S1/E1 | 6 | 102124 |
| 2007/12/23 | S1/E1 | 4 | 102124 | |
| 2008/04/19 | W1/S1 | 8 | 102124 | |
| 2008/04/22 | S1/E1 | 9 | 102124 | |
| 2008/04/23 | S1/E1 | 7 | 102634 | |
| 103095 | 2007/11/16 | S1/E1 | 7 | 103799 |
| 2007/12/24 | S1/E1 | 10 | 103799 | |
| 109358 | 2007/05/26 | S1/E2 | 3 | 110897 |
| 2008/04/18 | W1/S1 | 5 | 103799, 110897 | |
| 114710 | 2008/04/21 | W1/S1 | 10 | 114093 |
| 2008/06/27 | S1/E1 | 6 | 114093 | |
| 118098 | 2007/03/10 | S1/E1 | 6 | 120066 |
| 2007/03/30 | S1/E1 | 5 | 120066 | |
| 2007/12/23 | S1/E1 | 2 | 120066 | |
| 2010/04/10 | S1/E1 | 4 | 116831, 120066 | |
| 126660 | 2007/05/24 | W1/S1 | 5 | 132254 |
| 2007/07/16 | S1/E1 | 6 | 132254 | |
| 2008/07/25 | S1/E1 | 4 | 132254 | |
| 128167 | 2008/06/28 | S1/E1 | 5 | 128093 |
| 2008/07/06 | S1/E1 | 12 | 128093 | |
| 2008/07/24 | S1/E2 | 10 | 128093 | |
| 131156 | 2007/03/12 | S1/E1 | 5 | 135101 |
| 2008/04/18 | W1/S1 | 5 | 135101, 129153 | |
| 2008/04/19 | W1/S1 | 6 | 135101 | |
| 2008/06/27 | S1/E1 | 9 | 135101, 129153 | |
| 141795 | 2008/07/22 | S1/E1 | 8 | 140775 |
| 142860 | 2007/07/20 | S1/E1 | 3 | 139225 |
| 2007/07/21 | S1/E1 | 6 | 139225 | |
| 2008/04/21 | W1/S1 | 10 | 139225 | |
| 146233 | 2008/04/19 | W1/S1 | 11 | 145607, 150177 |
| 2008/04/21 | W1/S1 | 6 | 145607, 150177 | |
| 2008/04/22 | S1/E1 | 9 | 145607, 150177 | |
| 2008/04/23 | S1/E1 | 6 | 145607, 150177 | |
| 2008/05/16 | W1/E2 | 4 | 150177 | |
| 162003 | 2007/07/17 | S1/E1 | 8 | 154099 |
| 2007/07/18 | S1/E1 | 2 | 162004 | |
| 2007/10/10 | W1/E1 | 6 | 162004 | |
| 2007/11/17 | S1/E1 | 4 | 162004 | |
| 2008/06/26 | S1/E1 | 5 | 162004 | |
| 164259 | 2008/04/22 | S1/E1 | 6 | 167564, 158352 |
| 2008/04/23 | S1/E1 | 3 | 158352 | |
| 2008/06/20 | W1/S1 | 3 | 158352 | |
| 2008/06/28 | S1/E1 | 5 | 158352 | |
| 2008/07/27 | W1/S1 | 6 | 158352 | |
| 173667 | 2007/07/20 | S1/E1 | 3 | 180317 |
| 2007/07/21 | S1/E1 | 9 | 176303 | |
| 2008/04/21 | W1/S1 | 3 | 176303 | |
| 2008/06/28 | S1/E1 | 8 | 176303 | |
| 2008/07/07 | W1/S1 | 1 | 176303 | |
| 2008/07/21 | W1/S1 | 1 | 176303 | |
| 2008/07/22 | S1/E1 | 6 | 176303 | |
| 2008/07/23 | W1/E1 | 6 | 176303 | |
| 177724 | 2008/06/28 | S1/E1 | 10 | 176303 |
| 2008/07/07 | W1/S1 | 5 | 176303 | |
| 2008/07/21 | W1/S1 | 4 | 176303 | |
| 2008/07/22 | S1/E1 | 6 | 176303 | |
| 2008/07/23 | W1/E1 | 6 | 176303 | |
| 2008/10/01 | S1/E1 | 4 | 176303 | |
| 182572 | 2007/07/21 | S1/E1 | 6 | 174897 |
| 2007/09/09 | S1/E1 | 10 | 174897 | |
| 2008/07/22 | S1/E1 | 5 | 174897 | |
| 2008/07/24 | S1/E2 | 5 | 174897 | |
| 2008/09/30 | S1/E1 | 7 | 176303 | |
| 185144 | 2007/05/24 | W1/S1 | 3 | 193664 |
| 2007/05/25 | W1/S1 | 4 | 193664 | |
| 2007/06/28 | W1/E1 | 1 | 193664 | |
| 2007/06/29 | W1/E1 | 4 | 193664 | |
| 2007/06/30 | W1/E1 | 1 | 193664 | |
| 2007/07/01 | W1/E1 | 2 | 193664 | |
| 185395 | 2007/05/26 | S1/E2 | 3 | 183534 |
| 2007/07/19 | S1/E1 | 11 | 191195 | |
| 2007/11/02 | W1/E2 | 5 | 191195 | |
| 2008/07/25 | S1/E1 | 8 | 191195 | |
| 201091 | 2007/06/30 | W1/E1 | 3 | 204485 |
| 201092 | 2007/06/30 | W1/E1 | 3 | 204485 |
| 210418 | 2008/06/28 | S1/E1 | 6 | 211976 |
| 2008/07/22 | S1/E1 | 9 | 211976 | |
| 2008/07/24 | S1/E2 | 4 | 211976 | |
| 2008/10/01 | S1/E1 | 3 | 211976 | |
| 213558 | 2007/09/08 | S1/E1 | 7 | 218470 |
| 2007/10/10 | W1/E1 | 10 | 210715 | |
| 2007/12/24 | S1/E1 | 6 | 218470 | |
| 2008/07/21 | S1/E1 | 5 | 218470 | |
| 215648 | 2007/07/16 | S1/E1 | 4 | 211976 |
| 2007/07/21 | S1/E1 | 14 | 214923 | |
| 2008/07/24 | S1/E2 | 5 | 214923 | |
| 2008/09/30 | S1/E1 | 4 | 211976 | |
| 2008/10/01 | S1/E1 | 8 | 211976, 216735 | |
| 222368 | 2006/12/07 | S1/E1 | 4 | 222603 |
| 2007/07/20 | S1/E1 | 11 | 222603 | |
| 2007/09/09 | S1/E1 | 5 | 222603 | |
| 2008/09/30 | S1/E1 | 10 | 222603, 225003 | |
| 2008/10/01 | S1/E1 | 8 | 216735 |
Note. Refer to Section 2.3 for details.
The observing log is shown in Table 3 and lists the identifications of the 44 stars observed in this work (Column 1), UT date (Column 2), CHARA baseline (Column 3), number of brackets (Column 4), and the calibrator(s) used on that date (Column 5). The specifics of the CHARA baseline configurations are displayed in Table 4. We include the observations of HD 6582, HD 10780, and HD 185144 here for completeness, because they are an original part of this survey, but their results have been previously presented in Boyajian et al. (2008).
Table 4. CHARA Baseline Configurations
| Telescope | B | ψ |
|---|---|---|
| Pair | (m) | (°) |
| W2/E2 | 156.28 | 63.3 |
| S2/E2 | 248.13 | 17.7 |
| W1/E2 | 251.34 | 77.6 |
| W1/S1 | 278.50 | 320.9 |
| S1/E2 | 278.77 | 14.5 |
| W1/E1 | 313.54 | 253.2 |
| S1/E1 | 330.67 | 22.1 |
Download table as: ASCIITypeset image
3. ANGULAR DIAMETERS
Angular diameters for each star were determined by fitting our interferometric measurements to the visibility curve for a single star's uniform disk θUD and limb-darkened θLD (Hanbury Brown et al. 1974b) angular diameters from the calibrated visibilities by χ2 minimization (Markwardt 2009). To account for limb darkening, we use the K-band limb-darkening coefficients computed in Claret (2000). Limb-darkening corrections are at the 2% level in the infrared, and for these types of stars the uncertainty of this correction is at most a tenth of a percent, well within our error budget.
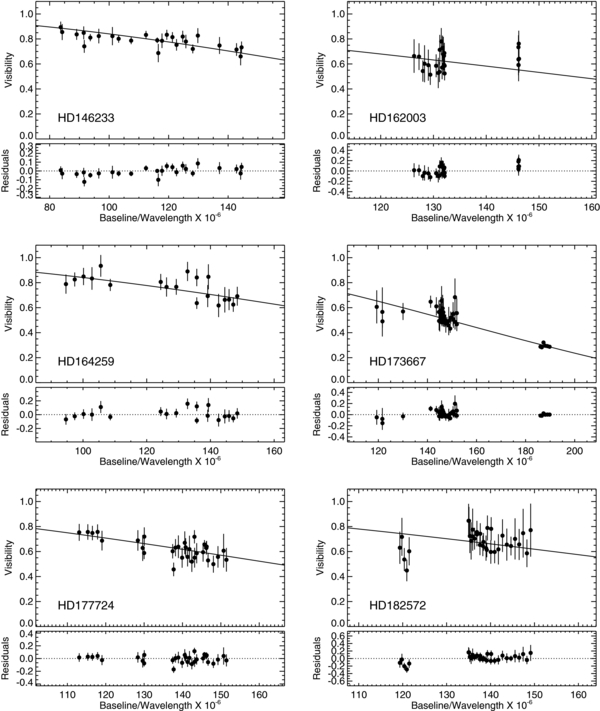
We find that in most cases the value of the reduced χ2 is less than 1.0, meaning that we have overestimated the errors on the calculated visibilities for the star. The results presented here adjust those error estimates to assume a reduced χ2 = 1 to compensate for the uncertainty in the visibility error estimates (Berger et al. 2006). Table 5 presents the total number of observations, reduced χ2, uniform disk diameter θUD, limb-darkening coefficient μK, and limb-darkened diameter θLD for each star. The resulting fit for each star is plotted in Figure 1. Overall, we successfully measure the angular diameters of 8 A stars, 20 F stars, and 16 G stars, with an average precision of ∼1.5%.
Download figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageFigure 1. Calibrated observations plotted with the limb-darkened angular diameter fit for each star observed. See Section 3 and Table 5 for details.
Download figure:
Standard image High-resolution imageTable 5. Angular Diameters
| Star | No. of | Reduced | θUD ± σ | μK | θLD ± σ |
|---|---|---|---|---|---|
| HD | Observations | χ2 | (mas) | (mas) | |
| 4614 | 27 | 1.43 | 1.578 ± 0.004 | 0.280 | 1.623 ± 0.004 |
| 5015 | 22 | 0.45 | 0.846 ± 0.010 | 0.270 | 0.865 ± 0.010 |
| 6582 | 26 | 0.96 | 0.947 ± 0.009 | 0.320 | 0.972 ± 0.009 |
| 10780 | 22 | 0.78 | 0.744 ± 0.018 | 0.310 | 0.763 ± 0.019 |
| 16895 | 21 | 1.02 | 1.078 ± 0.008 | 0.270 | 1.103 ± 0.009 |
| 19373 | 22 | 0.90 | 1.217 ± 0.007 | 0.270 | 1.246 ± 0.008 |
| 20630 | 21 | 1.15 | 0.914 ± 0.024 | 0.290 | 0.936 ± 0.025 |
| 22484 | 23 | 1.05 | 1.056 ± 0.014 | 0.280 | 1.081 ± 0.014 |
| 30652 | 34 | 0.60 | 1.488 ± 0.004 | 0.260 | 1.526 ± 0.004 |
| 34411 | 18 | 1.07 | 0.958 ± 0.015 | 0.290 | 0.981 ± 0.015 |
| 39587 | 17 | 0.33 | 1.027 ± 0.009 | 0.280 | 1.051 ± 0.009 |
| 48737 | 24 | 1.49 | 1.369 ± 0.009 | 0.180 | 1.401 ± 0.009 |
| 56537 | 20 | 0.52 | 0.824 ± 0.013 | 0.250 | 0.835 ± 0.013 |
| 58946 | 15 | 0.51 | 0.837 ± 0.013 | 0.230 | 0.853 ± 0.014 |
| 81937 | 18 | 0.34 | 1.113 ± 0.009 | 0.260 | 1.133 ± 0.009 |
| 82328 | 19 | 0.54 | 1.591 ± 0.005 | 0.320 | 1.632 ± 0.005 |
| 82885 | 25 | 0.45 | 0.800 ± 0.012 | 0.290 | 0.821 ± 0.013 |
| 86728 | 28 | 0.62 | 0.753 ± 0.012 | 0.260 | 0.771 ± 0.012 |
| 90839 | 19 | 0.38 | 0.778 ± 0.014 | 0.180 | 0.794 ± 0.014 |
| 95418 | 29 | 1.41 | 1.133 ± 0.014 | 0.210 | 1.149 ± 0.014 |
| 97603 | 16 | 1.59 | 1.304 ± 0.008 | 0.310 | 1.328 ± 0.009 |
| 101501 | 10 | 0.22 | 0.887 ± 0.009 | 0.270 | 0.910 ± 0.009 |
| 102870 | 32 | 0.54 | 1.396 ± 0.006 | 0.320 | 1.431 ± 0.006 |
| 103095 | 16 | 0.08 | 0.679 ± 0.005 | 0.280 | 0.696 ± 0.005 |
| 109358 | 12 | 1.97 | 1.209 ± 0.030 | 0.280 | 1.238 ± 0.030 |
| 114710 | 16 | 0.40 | 1.100 ± 0.011 | 0.180 | 1.127 ± 0.011 |
| 118098 | 15 | 0.17 | 0.840 ± 0.009 | 0.260 | 0.852 ± 0.009 |
| 126660 | 15 | 0.43 | 1.086 ± 0.007 | 0.250 | 1.109 ± 0.007 |
| 128167 | 26 | 0.40 | 0.824 ± 0.013 | 0.320 | 0.841 ± 0.013 |
| 131156 | 30 | 1.92 | 1.163 ± 0.014 | 0.210 | 1.196 ± 0.014 |
| 141795 | 8 | 0.10 | 0.756 ± 0.017 | 0.260 | 0.768 ± 0.017 |
| 142860 | 19 | 0.11 | 1.191 ± 0.005 | 0.290 | 1.217 ± 0.005 |
| 146233 | 25 | 0.46 | 0.763 ± 0.017 | 0.250 | 0.780 ± 0.017 |
| 162003 | 25 | 2.23 | 0.930 ± 0.025 | 0.240 | 0.949 ± 0.026 |
| 164259 | 19 | 0.56 | 0.761 ± 0.027 | 0.250 | 0.775 ± 0.027 |
| 173667 | 42 | 1.06 | 0.979 ± 0.006 | 0.170 | 1.000 ± 0.006 |
| 177724 | 31 | 1.05 | 0.883 ± 0.016 | 0.320 | 0.895 ± 0.017 |
| 182572 | 33 | 1.91 | 0.823 ± 0.025 | 0.320 | 0.845 ± 0.025 |
| 185144 | 15 | 1.00 | 1.219 ± 0.011 | 0.240 | 1.254 ± 0.012 |
| 185395 | 25 | 0.86 | 0.845 ± 0.015 | 0.200 | 0.861 ± 0.015 |
| 210418 | 20 | 0.32 | 0.849 ± 0.017 | 0.180 | 0.862 ± 0.018 |
| 213558 | 27 | 0.84 | 0.625 ± 0.021 | 0.260 | 0.634 ± 0.022 |
| 215648 | 34 | 1.06 | 1.068 ± 0.008 | 0.260 | 1.091 ± 0.008 |
| 222368 | 36 | 0.90 | 1.059 ± 0.009 | 0.260 | 1.082 ± 0.009 |
Note. Refer to Section 3 for details.
Download table as: ASCIITypeset image
3.1. Notes on Individual Star Groups
3.1.1. A Stars
The results for the A-type stars (eight total) are special cases. A-type stars are approaching the range at which stars begin to be seen with the highest rotational velocities (B-type stars), resulting in oblate shapes and apparent gravity darkening due to their rapid rotation (for example, see Zhao et al. 2009). This oblateness factor depends on the star's θLD, rotational velocity v sin i, and mass (see Equation (5) in Absil et al. 2008). The most extreme case that we observed is HD 177724, which is among one of the fastest rotating A stars, with a rotational velocity v sin i = 317 km s−1 (Royer et al. 2006), which leads to a predicted apparent oblateness of 1.307 (Absil et al. 2008). Using all measurements and assuming the object to be round, we present the mean diameter for HD 177724 of θLD = 0.897 ± 0.017 mas (Table 5). This value is in excellent agreement with the predicted mean angular diameter from Absil et al. (2008) of θ = 0.880 ± 0.018 mas. The rotational velocity for all of the A stars in this project (except for HD 141795; v sin i = 47 km s−1) are fairly high (HD 56537 = 154 km s−1, HD 97603 = 180 km s−1, HD 118098 = 222 km s−1, HD 210418 = 144 km s−1, and HD 213558 = 128 km s−1; Royer et al. 2006). Although their predicted oblateness is likely to be undetectable with the precision of our measurements, we should consider the angular diameter measured for these stars as the mean angular diameter. The rotational velocities of the F- and G-type stars observed are far below the critical, therefore they are assumed to be round.
3.1.2. Multiplicity
Our targets were selected to only include single stars because incoherent light from a companion affects the visibility of the primary star and biases the diameter measurement. We admit binary stars only with separations greater than 2 arcsec or with large ΔK magnitudes.13 For example, the star HD 39587 (G0 V + M5 V; Han & Gatewood 2002) is a single-lined spectroscopic binary. Our data do not reveal the imprint of a companion (reduced χ2 = 0.33), and the diameter is assumed to be unaffected by the presence of a secondary star with the assumption that the Δ magnitude is quite large (ΔK > 4 mag).
The diameter fit for the star HD 162003 has the largest reduced χ2 of 2.23. Very recent radial velocity survey work has identified HD 162003 to have a long-term trend in radial velocity of +220 m s−1 yr−1 (Toyota et al. 2009).14 We suspect that the reason our diameter fit for this star shows the highest value of reduced χ2 is that we are actually detecting a mild signature of the secondary star in the visibilities. Another target in this survey HD 173667 is identified by Nidever et al. (2002) to have σrms = 124 m s−1 over a period of 5165 days. However, unlike the diameter fit for HD 162003, the reduced χ2 is typical of a fit from a single star (reduced χ2 = 1.34). Lastly, we note that the stars HD 4614 and HD 10935815 were once referred to as spectroscopic binaries by Abt & Levy (1976). However, Morbey & Griffin (1987) disputed this result, and HD 109358 is now used as a radial velocity standard (for example, see Behr et al. 2009; Konacki 2005).
3.2. CHARA versus Palomar Testbed Interferometer Diameters
Angular diameters of a few dozen main-sequence stars measured with the Palomar Testbed Interferometer (PTI) were presented by van Belle & von Braun (2009). Their work provides measurements of 14 stars in common with the CHARA stars measured here and is the only alternate source of direct angular diameter measurements of our program stars. The longest baseline obtainable with PTI is 110 m, a factor of three shorter than those of the CHARA Array, and accurate measurements were quite difficult with this instrument due to the small angular sizes of these stars.
Table 6 lists the 14 stars in common with van Belle & von Braun (2009), the limb-darkened angular diameters and errors, and how many σ the two values differ from each other. For these stars, the errors on the PTI angular diameters are anywhere from 2 to 12 times (with an average of 6.5 times) the errors on the CHARA angular diameters. However, this comparison can still point to any systematic offsets in the results from each instrument. Comparing the angular diameters from this work and van Belle & von Braun (2009), we find that the weighted mean ratio of CHARA to PTI diameters is θCHARA/θPTI = 1.052 ± 0.062. Van Belle & von Braun (2009) make this same comparison of their diameters compared to diameters from Baines et al. (2008), who used the CHARA Array to measure the diameters of exoplanet host stars, and find that the ratio of the four stars they have in common is θCHARA/θPTI = 1.06 ± 0.06, very similar to the results found here, indicating again that there is a slight preference for smaller PTI diameters, and larger CHARA diameters, although the displacement is at the <1σ level.
Table 6. CHARA versus PTI Angular Diameters
| HD | CHARA | Error | PTIa | Error | ΔθLD/σCb |
|---|---|---|---|---|---|
| θLD ± σ | (%) | θLD ± σ | (%) | ||
| 16895 | 1.103 ± 0.009 | 0.8 | 1.086 ± 0.056 | 5.2 | 0.3 |
| 19373 | 1.246 ± 0.008 | 0.6 | 1.331 ± 0.050 | 3.8 | −1.7 |
| 20630 | 0.936 ± 0.025 | 2.7 | 0.895 ± 0.070 | 7.8 | 0.6 |
| 22484 | 1.081 ± 0.014 | 1.3 | 0.911 ± 0.123 | 13.5 | 1.4 |
| 30652 | 1.526 ± 0.004 | 0.3 | 1.409 ± 0.048 | 3.4 | 2.4 |
| 39587 | 1.051 ± 0.009 | 0.9 | 1.124 ± 0.056 | 5.0 | −1.3 |
| 97603 | 1.328 ± 0.009 | 0.7 | 1.198 ± 0.053 | 4.4 | 2.4 |
| 109358 | 1.238 ± 0.030 | 2.4 | 1.138 ± 0.055 | 4.8 | 1.6 |
| 114710 | 1.127 ± 0.011 | 1.0 | 1.071 ± 0.057 | 5.3 | 1.0 |
| 126660 | 1.109 ± 0.007 | 0.6 | 1.130 ± 0.055 | 4.9 | −0.4 |
| 142860 | 1.217 ± 0.005 | 0.4 | 1.161 ± 0.054 | 4.7 | 1.0 |
| 185144 | 1.254 ± 0.012 | 1.0 | 1.092 ± 0.057 | 5.2 | 2.8 |
| 215648 | 1.091 ± 0.008 | 0.7 | 1.022 ± 0.059 | 5.8 | 1.2 |
| 222368 | 1.082 ± 0.009 | 0.8 | 1.062 ± 0.057 | 5.4 | 0.3 |
Notes. Refer to Section 3.2 for details. aFrom van Belle & von Braun (2009). bHere, ΔθLD is the difference between PTI and CHARA limb-darkened angular diameters, and σC is the combined error, σC = (σ2CHARA + σ2PTI)0.5.
Download table as: ASCIITypeset image
The preference to larger diameters compared to other interferometric measurements was also seen in Boyajian et al. (2009), where the diameters of the four Hyades giants were measured with the CHARA Array. In that work, two of the stars,  Tau and δ1 Tau, were measured previously with other interferometers (Mark III, NPOI, and PTI), all of which lead to smaller diameters than those measured with CHARA. However, Boyajian et al. (2009) find that models for the Hyades age and metallicity match flawlessly with the CHARA observations, and the smaller angular diameters from other works in turn lead to temperatures that are too hot for these stars.
Tau and δ1 Tau, were measured previously with other interferometers (Mark III, NPOI, and PTI), all of which lead to smaller diameters than those measured with CHARA. However, Boyajian et al. (2009) find that models for the Hyades age and metallicity match flawlessly with the CHARA observations, and the smaller angular diameters from other works in turn lead to temperatures that are too hot for these stars.
A main distinction that could lead to offsets in measured diameters is the estimated size of the calibrator stars. For instance, van Belle & von Braun (2009) discuss the calibrator selection in their work compared to Baines et al. (2008). Van Belle & von Braun (2009) set a limit to a sufficiently unresolved calibrator at CHARA to be <0.5 mas in diameter, a criterion which all but a few calibrators in this work meet. However, to investigate the possibility that the estimated size of the calibrators in this work is offset to the calibrators used in van Belle & von Braun (2009), we compare the estimated sizes of the calibrators in the Palomar Testbed Interferometer Calibrator Catalog (PTICC; van Belle et al. 2008) to the ones derived here. Twenty-nine of the 63 calibrators used in this work are included in the PTICC. Overall, the ratio of the estimated diameter of the calibrator in this work to the PTICC is 0.97 ± 0.06, a less than 1σ difference.
Twelve of the 14 stars in common with van Belle & von Braun (2009) were observed with calibrators whose diameters are also included in the PTICC. For each of these 12 calibrators, the estimated angular diameter θSED is presented in Table 7, along with the ratio of the CHARA to PTI SED diameters. The object employing the calibrator is also listed in Table 7 along with the ratio of the CHARA to PTI measured limb-darkened diameters. Here, there is no pattern in the calibrator SED diameter ratio and the object diameter ratio. In fact, the effects of a slight offset in the calibrator's estimated diameter listed above (ratio θCHARA/θPTI = 0.97 ± 0.06) would actually contribute counterproductively to the slight offset in the diameter measurements (ratio θCHARA/θPTI = 1.05 ± 0.06). For instance, in the case of our data, the size of the calibrator θSED is typically smaller, thus the true visibility of the calibrator would be greater (i.e., it would be more unresolved). If the true visibility of the calibrator is greater, it would in turn make the true visibility of the object larger in the calibration process. Thus, the object would appear more unresolved (having larger calibrated visibilities) if we were using a SED diameter of the same calibrator but with a larger value. Because we do not see the case of smaller CHARA diameters, this indicates that the calibrators are not the cause of any offset, if present, in each data set.
Table 7. CHARA versus PTI Calibrators
| Calibrator | CHARA | PTIa | Calibrator SED | Object | Object Measured |
|---|---|---|---|---|---|
| HD | θSED (mas) | θSED (mas) | θCHARA/θPTI | HD | θCHARA/θPTIb |
| 20675 | 0.415 ± 0.012 | 0.424 ± 0.020 | 0.98 ± 0.05 | 16895 | 1.02 ± 0.05 |
| 20675 | 0.415 ± 0.012 | 0.424 ± 0.020 | 0.98 ± 0.05 | 19373 | 0.94 ± 0.04 |
| 22879 | 0.342 ± 0.021 | 0.369 ± 0.009 | 0.93 ± 0.06 | 20630 | 1.05 ± 0.09 |
| 22879 | 0.342 ± 0.021 | 0.369 ± 0.009 | 0.93 ± 0.06 | 22484 | 1.19 ± 0.16 |
| 28355 | 0.425 ± 0.030 | 0.401 ± 0.012 | 1.06 ± 0.08 | 30652 | 1.08 ± 0.04 |
| 30739 | 0.461 ± 0.018 | 0.544 ± 0.025 | 0.85 ± 0.05 | 30652 | 1.08 ± 0.04 |
| 31295 | 0.439 ± 0.043 | 0.470 ± 0.022 | 0.93 ± 0.10 | 30652 | 1.08 ± 0.04 |
| 38558 | 0.422 ± 0.008 | 0.442 ± 0.033 | 0.95 ± 0.07 | 39587 | 0.94 ± 0.05 |
| 43042 | 0.591 ± 0.030 | 0.655 ± 0.017 | 0.90 ± 0.05 | 39587 | 0.94 ± 0.05 |
| 99285 | 0.456 ± 0.017 | 0.454 ± 0.026 | 1.00 ± 0.07 | 97603 | 1.11 ± 0.05 |
| 110897 | 0.492 ± 0.022 | 0.504 ± 0.009 | 0.98 ± 0.05 | 109358 | 1.09 ± 0.06 |
| 132254 | 0.520 ± 0.015 | 0.542 ± 0.013 | 0.96 ± 0.04 | 126660 | 0.98 ± 0.05 |
| 193664 | 0.494 ± 0.019 | 0.552 ± 0.011 | 0.89 ± 0.04 | 185144 | 1.15 ± 0.06 |
| 211976 | 0.373 ± 0.013 | 0.377 ± 0.009 | 0.99 ± 0.04 | 215648 | 1.07 ± 0.06 |
| 214923 | 0.611 ± 0.029 | 0.552 ± 0.094 | 1.11 ± 0.20 | 215648 | 1.07 ± 0.06 |
| 216735 | 0.321 ± 0.022 | 0.330 ± 0.020 | 0.97 ± 0.09 | 215648 | 1.07 ± 0.06 |
| 216735 | 0.321 ± 0.022 | 0.330 ± 0.020 | 0.97 ± 0.09 | 222368 | 1.02 ± 0.06 |
| 222603 | 0.577 ± 0.032 | 0.533 ± 0.014 | 1.08 ± 0.07 | 222368 | 1.02 ± 0.06 |
Notes. Refer to Section 3.2 for details. aFrom the PTICC (van Belle et al. 2008). bThe limb-darkened diameter presented here versus the value in van Belle & von Braun (2009).
Download table as: ASCIITypeset image
In Figure 2, we show a plot of the measured limb-darkened angular diameters presented here compared to the computed SED diameters for the stars in this survey. The 14 stars in common with the van Belle & von Braun (2009) work are highlighted in color, red indicating a CHARA measurement and blue for a PTI measurement. It is apparent here that the majority of the PTI diameters are deceptively low compared to the SED estimates.
Figure 2. Top: plot showing the measured limb-darkened angular diameters vs. the SED angular diameters and the 1σ errors (black). Measurements for the 14 stars in common with this work are highlighted in color with red indicating a CHARA measurement presented in this paper and blue for a PTI measurement measured in van Belle & von Braun (2009). Bottom: plot showing the fractional difference between the SED and limb-darkened angular diameters. The dotted line shows an equal agreement of both measurements. See Section 3.2 and Tables 5 and 6 for details.
Download figure:
Standard image High-resolution imageFigure 3 shows the fractional difference of the measured limb-darkened versus SED angular diameter as a function of (B − V) color index. For stars with a (B − V) <0.4, the measured θLD is always larger than the estimated θSED. There is a lot of scatter for stars redder than (B − V) ∼0.4, but no systematics are seen. However, in this region the two most metal-poor stars, HD 6582 and HD 103095, are the most extreme outliers, where θLD > θSED in both cases. Additionally, HD 182572 (B − V = 0.761; [Fe/H] = 0.33) is the most metal-rich star observed in this work and shows the largest disagreement here where θLD < θSED. Perhaps there is a lack of sufficient data to show if there is in fact a trend in either the color index or metallicity of a star and the estimated θSED.
Figure 3. Top: the difference between limb-darkened angular diameters and the SED angular diameters from this work vs. (B − V) color index. Bottom: the same as above with respect to metallicity. The dotted line shows an equal agreement of both measurements. A provisional fit to the data is shown as a solid line and is suspect to a cautious interpretation due to the sparse amount of data available. See Section 3 for details.
Download figure:
Standard image High-resolution image4. STELLAR PARAMETERS
4.1. Bolometric Fluxes
We present new measures of the bolometric flux FBOL for each star in this work that follows the method used previously in support of interferometric observations (van Belle et al. 2008; van Belle & von Braun 2009). The fit involves a collection of flux-calibrated photometry for each source available in the literature (see Table 8) that is subsequently fit with a template spectra from the Pickles (1998) library. Reddening is for the most part absent for the sample;16 however, we fit it here to the photometric data using reddening corrections based upon the empirical reddening determination described by Cardelli et al. (1989), which differs little from van de Hulst's theoretical reddening curve number 15 (Johnson 1968; Dyck et al. 1996).
Uncertainties in FBOL are for our data, on average 1.9%, and tend to be dominated by uncertainty in the reddening fit and poor photometry in the 0.6–1.2 μm range. Each science object is listed in Table 9 along with the fitting parameters: Pickles (1998) template spectral type, number of photometry points, and reduced χ2 of the fit, as well as the resulting integrated FBOL and AV. In Figure 4, we show an example SED fit.
Figure 4. Example of SED fit for HD 142860. The (red) pluses indicate flux-calibrated photometry from the literature with corresponding errors (y-direction) and bandwidth of the filter (x-direction). The (black) crosses show the flux value of the spectral template integrated over the filter transmission for each point. The spectral template is plotted by a blue line. The lower panel shows the residuals. See Section 4 for details.
Download figure:
Standard image High-resolution image4.2. Luminosities, Temperatures, and Radii
These FBOL measurements are then simply used in combination with the Hipparcos distance d to solve for the absolute luminosity L:
Additionally, we can express the effective temperature of a star as defined through the Stephan–Boltzmann law:
where F is the total emergent flux of the star and σ is the Stefan–Boltzmann constant. Transforming this equation to observables at Earth, we arrive at the expression
The effective temperature TEFF is found by solving Equation (5) in terms of FBOL and θLD, where in Equation (6), FBOL is in units of 10−8 erg s−1 cm−2 and θLD is in units of mas. This yields the relation
Finally, using Hipparcos parallaxes from van Leeuwen (2007), we transform the measured angular diameters of these stars into linear radii R. Each of these derived parameters are presented in Table 10. Graphical representations of these data sets are presented in Figures 5 and 6.
Figure 5. Luminosities and temperatures of the stars in the survey are plotted with their 1σ errors. Lines of constant radii are plotted as dotted lines. The shading of the symbol represents the metallicity of the star [Fe/H]. See Section 4.2 for details.
Download figure:
Standard image High-resolution imageFigure 6. Luminosity and (B − V) color index plotted of the stars in this survey. The shading of the symbol represents the metallicity of the star [Fe/H]. See Section 4.2 for details.
Download figure:
Standard image High-resolution imageTable 8. Target Photometry
| Object | System/ | Bandpass | Value | Error | Reference |
|---|---|---|---|---|---|
| HD | Wavelength | Bandwidth | (mag) | (mag) | |
| HD 4614 | 1240 | 248 | 2.41 | 0.05 | Selby et al. (1988) |
| HD 4614 | 1250 | 250 | 2.36 | 0.05 | Johnson (1965b) |
| HD 4614 | 1250 | 250 | 2.36 | 0.05 | Johnson et al. (1966) |
| HD 4614 | 1250 | 250 | 2.35 | 0.05 | Johnson et al. (1968) |
| HD 4614 | 1250 | 250 | 2.35 | 0.05 | Voelcker (1975) |
| HD 4614 | 1250 | 250 | 2.41 | 0.05 | Blackwell et al. (1990) |
| HD 4614 | 1270 | 254 | 2.35 | 0.05 | Bergeat & Lunel (1980) |
| HD 4614 | 1620 | 324 | 2.02 | 0.05 | Bergeat & Lunel (1980) |
| HD 4614 | 1650 | 330 | 2.02 | 0.05 | Johnson et al. (1968) |
| HD 4614 | 1650 | 330 | 2.02 | 0.05 | Voelcker (1975) |
Notes. Refer to Section 2.3 for details.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 9. Bolometric Fluxes
| Star | Template | No. of | Reduced | FBOL ± σ | AV ± σ |
|---|---|---|---|---|---|
| HD | Sp.Ty. | PHOT | χ2 | (10−8 erg s−1 cm−2) | (mag) |
| 4614 | G0V | 80 | 1.04 | 113.90 ± 1.71 | 0.001 ± 0.014 |
| 5015 | F8V | 95 | 0.74 | 31.50 ± 0.56 | 0.005 ± 0.016 |
| 6582 | G5V | 165 | 2.63 | 24.48 ± 0.39 | 0.000 ± 0.014 |
| 10780 | K0V | 86 | 0.75 | 16.43 ± 0.33 | 0.000 ± 0.018 |
| 16895 | F6V | 94 | 0.70 | 58.21 ± 1.04 | 0.000 ± 0.016 |
| 19373 | G0V | 89 | 0.41 | 63.29 ± 0.93 | 0.016 ± 0.013 |
| 20630 | G5V | 205 | 0.59 | 32.46 ± 0.55 | 0.000 ± 0.015 |
| 22484 | G0V | 171 | 0.33 | 51.23 ± 0.69 | 0.000 ± 0.012 |
| 30652 | F6V | 251 | 0.72 | 139.80 ± 1.50 | 0.000 ± 0.009 |
| 34411 | G1V | 151 | 0.49 | 35.01 ± 0.45 | 0.000 ± 0.011 |
| 39587 | G0V | 139 | 0.28 | 46.44 ± 0.78 | 0.011 ± 0.015 |
| 48737 | F5III | 85 | 0.60 | 115.20 ± 2.37 | 0.000 ± 0.018 |
| 56537 | A5V | 136 | 1.11 | 95.40 ± 2.18 | 0.000 ± 0.019 |
| 58946 | F0V | 156 | 0.41 | 54.87 ± 0.88 | 0.020 ± 0.014 |
| 81937 | F02IV | 69 | 1.69 | 85.77 ± 1.88 | 0.035 ± 0.019 |
| 82328 | F6.5IV | 96 | 0.32 | 139.70 ± 2.81 | 0.000 ± 0.018 |
| 82885 | G8V | 189 | 1.32 | 19.57 ± 0.18 | 0.032 ± 0.008 |
| 86728 | G5V | 150 | 0.26 | 19.63 ± 0.39 | 0.000 ± 0.017 |
| 90839 | F8V | 83 | 0.43 | 31.69 ± 0.82 | 0.000 ± 0.023 |
| 95418 | A0IV | 106 | 0.82 | 339.90 ± 7.05 | 0.038 ± 0.017 |
| 97603 | A4V | 105 | 1.55 | 250.90 ± 3.87 | 0.053 ± 0.013 |
| 101501 | G6.5V | 138 | 0.41 | 21.27 ± 0.30 | 0.011 ± 0.012 |
| 102870 | G0V | 222 | 0.35 | 96.43 ± 1.41 | 0.000 ± 0.013 |
| 103095 | G9V | 244 | 3.85 | 8.27 ± 0.08 | 0.000 ± 0.009 |
| 109358 | G0V | 137 | 0.57 | 52.11 ± 0.84 | 0.000 ± 0.014 |
| 114710 | G0V | 216 | 0.43 | 52.49 ± 0.56 | 0.000 ± 0.010 |
| 118098 | A5V | 104 | 2.29 | 111.80 ± 1.57 | 0.000 ± 0.013 |
| 126660 | F7V | 98 | 0.50 | 63.08 ± 1.47 | 0.000 ± 0.020 |
| 128167 | F2V | 182 | 1.88 | 44.52 ± 0.54 | 0.062 ± 0.010 |
| 131156 | G8V | 90 | 1.45 | 46.18 ± 1.05 | 0.043 ± 0.019 |
| 141795 | A5V | 101 | 1.13 | 83.87 ± 2.05 | 0.020 ± 0.020 |
| 142860 | F6V | 156 | 0.31 | 77.38 ± 1.30 | 0.014 ± 0.014 |
| 146233 | G3.5V | 116 | 0.62 | 17.65 ± 0.46 | 0.000 ± 0.022 |
| 162003 | F6V | 96 | 0.44 | 39.22 ± 0.95 | 0.000 ± 0.021 |
| 164259 | F3.5V | 134 | 0.43 | 36.34 ± 0.74 | 0.000 ± 0.018 |
| 173667 | F6V | 84 | 0.33 | 55.02 ± 1.19 | 0.002 ± 0.019 |
| 177724 | A0V | 163 | 1.16 | 191.50 ± 3.12 | 0.002 ± 0.014 |
| 182572 | G8IV | 95 | 1.86 | 26.66 ± 0.63 | 0.000 ± 0.021 |
| 185144 | K0V | 240 | 0.72 | 39.93 ± 0.56 | 0.000 ± 0.012 |
| 185395 | F2V | 143 | 0.25 | 40.91 ± 0.86 | 0.015 ± 0.018 |
| 210418 | A2IV | 83 | 1.21 | 98.86 ± 2.46 | 0.000 ± 0.022 |
| 213558 | A0V | 109 | 0.94 | 93.04 ± 2.21 | 0.015 ± 0.020 |
| 215648 | F8V | 154 | 0.66 | 57.33 ± 1.05 | 0.000 ± 0.016 |
| 222368 | F8V | 279 | 0.40 | 60.95 ± 0.99 | 0.000 ± 0.014 |
Notes. For details, see Section 4.1.
Download table as: ASCIITypeset image
Table 10. Radii, Luminosities, and Temperatures
| Star | R | L | TEFF |
|---|---|---|---|
| HD | (R☉) | (L☉) | (K) |
| 4614 | 1.039 ± 0.004 | 1.252 ± 0.019 | 6003 ± 24 |
| 5015 | 1.743 ± 0.023 | 3.432 ± 0.061 | 5963 ± 44 |
| 6582 | 0.790 ± 0.009 | 0.428 ± 0.007 | 5264 ± 32 |
| 10780 | 0.825 ± 0.021 | 0.516 ± 0.010 | 5396 ± 72 |
| 16895 | 1.319 ± 0.011 | 2.235 ± 0.040 | 6157 ± 37 |
| 19373 | 1.412 ± 0.009 | 2.181 ± 0.032 | 5915 ± 29 |
| 20630 | 0.919 ± 0.025 | 0.841 ± 0.014 | 5776 ± 81 |
| 22484 | 1.622 ± 0.024 | 3.042 ± 0.042 | 5997 ± 44 |
| 30652 | 1.323 ± 0.004 | 2.822 ± 0.030 | 6516 ± 19 |
| 34411 | 1.331 ± 0.021 | 1.732 ± 0.022 | 5749 ± 48 |
| 39587 | 0.979 ± 0.009 | 1.081 ± 0.018 | 5961 ± 36 |
| 48737 | 2.710 ± 0.021 | 11.574 ± 0.238 | 6480 ± 39 |
| 56537 | 2.777 ± 0.047 | 28.306 ± 0.648 | 8007 ± 77 |
| 58946 | 1.655 ± 0.028 | 5.542 ± 0.089 | 6899 ± 63 |
| 81937 | 2.902 ± 0.026 | 15.086 ± 0.330 | 6693 ± 45 |
| 82328 | 2.365 ± 0.008 | 7.871 ± 0.158 | 6300 ± 33 |
| 82885 | 1.003 ± 0.016 | 0.784 ± 0.007 | 5434 ± 45 |
| 86728 | 1.247 ± 0.021 | 1.378 ± 0.027 | 5612 ± 52 |
| 90839 | 1.091 ± 0.020 | 1.605 ± 0.042 | 6233 ± 68 |
| 95418 | 3.021 ± 0.038 | 63.015 ± 1.307 | 9377 ± 75 |
| 97603 | 2.557 ± 0.020 | 24.973 ± 0.385 | 8085 ± 42 |
| 101501 | 0.940 ± 0.010 | 0.609 ± 0.009 | 5270 ± 32 |
| 102870 | 1.681 ± 0.008 | 3.572 ± 0.052 | 6132 ± 26 |
| 103095 | 0.681 ± 0.006 | 0.212 ± 0.002 | 4759 ± 20 |
| 109358 | 1.123 ± 0.028 | 1.151 ± 0.018 | 5653 ± 72 |
| 114710 | 1.106 ± 0.011 | 1.357 ± 0.014 | 5936 ± 33 |
| 118098 | 2.079 ± 0.025 | 17.885 ± 0.252 | 8247 ± 52 |
| 126660 | 1.733 ± 0.011 | 4.131 ± 0.096 | 6265 ± 41 |
| 128167 | 1.431 ± 0.023 | 3.461 ± 0.042 | 6594 ± 55 |
| 131156 | 0.863 ± 0.011 | 0.645 ± 0.015 | 5580 ± 46 |
| 141795 | 1.783 ± 0.040 | 12.134 ± 0.296 | 8084 ± 102 |
| 142860 | 1.472 ± 0.007 | 3.039 ± 0.051 | 6294 ± 29 |
| 146233 | 1.166 ± 0.026 | 1.058 ± 0.028 | 5433 ± 69 |
| 162003 | 2.329 ± 0.067 | 6.343 ± 0.153 | 6014 ± 90 |
| 164259 | 1.961 ± 0.071 | 6.251 ± 0.127 | 6529 ± 118 |
| 173667 | 2.064 ± 0.017 | 6.296 ± 0.136 | 6376 ± 39 |
| 177724 | 2.449 ± 0.046 | 38.492 ± 0.627 | 9205 ± 95 |
| 182572 | 1.379 ± 0.042 | 1.904 ± 0.045 | 5787 ± 92 |
| 185144 | 0.776 ± 0.008 | 0.410 ± 0.006 | 5255 ± 31 |
| 185395 | 1.697 ± 0.030 | 4.265 ± 0.090 | 6381 ± 65 |
| 210418 | 2.623 ± 0.083 | 24.549 ± 0.610 | 7951 ± 97 |
| 213558 | 2.143 ± 0.074 | 28.552 ± 0.678 | 9131 ± 167 |
| 215648 | 1.912 ± 0.016 | 4.722 ± 0.087 | 6167 ± 36 |
| 222368 | 1.595 ± 0.014 | 3.555 ± 0.058 | 6288 ± 37 |
Notes. For details, see Section 4.2.
Download table as: ASCIITypeset image
5. DISCUSSION
5.1. Empirical Temperature Relations
With the results in Table 10, we may begin to define a foundation of empirically based color–temperature relations. These relationships are extremely useful in extending our knowledge to a larger number of stars, at distances too far to accurately resolve their sizes. For giants and supergiants, temperature scales accurate to the 2.5% level are obtainable, and are currently limited by the distances to these objects, not the sensitivities of our interferometric observations (van Belle et al. 1999, 2009). Recently, and more similarly comparable to this work, van Belle & von Braun (2009) present relations for main-sequence stars, ranging from (V − K) ∼ 0.0 to 4.0 (spectral types of ∼A-M). These scales are slightly better than the aforementioned evolved classes of stars and are accurate to the ∼2% level. The authors note here that the limitations to these relations are in the angular diameter measurements themselves.
5.1.1. (B − V)–TEFF
Here, we derive color–temperature relations based on the precise TEFF measurements presented in Table 10 in the form of a sixth-order polynomial. The solution for the (B − V) color–temperature relation is expressed as
This solution, in the form of a sixth-order polynomial, defines the shape of the data inflection point at (B − V) ∼0.3 better than a lower order polynomial function, as well as a power-law function (see Figure 7). We are also cautious that the stars with low metallicity will affect the (B − V)–TEFF transformation too severely to be useful for stars of solar-type abundances, and we refrain from using these in this analysis.17 A preliminary fit to the data yields a median deviation in temperature of 68 K, and a median deviation in temperature of 55 K is found for an identical solution if we omit three obvious outliers lying more than 5σ away, HD 210418, HD 182572, and HD 162003 (offset of −6.7σ, −5.7σ, and +6.5σ, respectively). The statistical summary for the solution to the polynomial can be found in Table 11.18
Table 11. Solutions to TEFF Relations
| (B − V) | (V − K) | Spectral Type | |
|---|---|---|---|
| Equation in text | (8) | (9) | (10) |
| n ... | 39 | 44 | 41 |
| Range ... | 0.05–0.80a | 0.0–2.0 | A0–K0a |
| Reduced χ2 ... | 5.97 | 6.04 | 12.1 |
| Median dTEFF ... | 55 | 64 | 90 |
Notes. Refer to Section 5.1 for details. aMetallicity [Fe/H] >−0.75.
Download table as: ASCIITypeset image
In Figure 7, we show our data and the solution for the fit. We also show the solution from several other sources, Code et al. (1976), Gray (1992), and Lejeune et al. (1998). All the solutions shown here are approximately identical in the range of (B − V) >0.45.
Figure 7. Data and solution for the temperature–(B − V) relation shown as circles and a solid line, respectively. The data omitted from the fit are plotted as open circles and can be identified (from left to right) as HD 210418, HD 162003, HD 6582, HD 182572, and HD 103095. The inverted triangles show the data from Code et al. (1976) and the empirical solution based on these data is plotted as a dotted line. The 1σ errors in temperature are displayed, but are typically smaller than the data point. The dash-dotted line is the calibration presented in Gray (1992), using a menagerie of data sources (see reference). The solution for solar metallicity from Casagrande et al. (2010) is shown as a triple-dot-dashed line. The entirely model-based solution from Lejeune et al. (1998; dashed line) is also shown. For details, see Section 5.1.1 and Equation (8).
Download figure:
Standard image High-resolution imageSimilar to our work, the results from Code et al. (1976) are derived solely on empirical measurements. In that milestone paper, Code et al. (1976) measure the diameters of 32 stars using the NSII, all being objects hotter than the Sun and most having evolved luminosity classes. We show in Figure 7 the nine data points from Code et al. (1976) that have a (B − V) >0 (∼A-type and later) with luminosity class V or IV (eight A-type objects and one F-type object), as well as the fit from Code et al. (1976). Comparing this fit to ours, we note that it is a few hundred Kelvin hotter than our own for 0.05 < (B − V) <0.3, converging at the bluest range of (B − V) ∼0, as well as the reddest range (B − V) ∼0.4. The offset is likely strongly connected to the fit's dependence on the sparse amount of data in this intermediate range.
The function presented in Gray (1992) also uses a sixth-order polynomial to fit (B − V) to TEFF (their Equation (15.14)). This is a fit to a compilation of data, including the NSII data from Code et al. (1976), but mostly data obtained via the infrared flux method (IRFM; see Blackwell & Shallis 1977), yielding a semi-empirical approach in obtaining the angular diameter, and consequentially the effective temperature, of a star. There is an impressive correlation with our fit throughout the range of (B − V) colors. A deviation only begins to appear at the bluest colors ((B − V) ∼0). Our sample stops here, but it can be readily seen in Gray (1992) that there is another inflection point at this color index, producing a steeper curve at more negative color indices. Because of this, we caution against the use of the relation presented here for colors bluer than (B − V) <0.05.
As an update, the work presented in Casagrande et al. (2010) presents an excellent analysis and improvement to the IRFM temperature scales that have been proposed over the years. In Figure 7, we also show the Casagrande et al. (2010) solution for solar metallicity for comparison (valid in the ranges of (B − V) > 0.3). This relation is distinguishable from ours only when 0.3 < (B − V) < 0.4, where at this point, the Casagrande et al. (2010) relation begins to predict ∼100 K higher temperatures. However, we suspect that the likely explanation for this difference is that their solution is in the form of a third-order polynomial, which has been shown not to model the inflection point in this region properly.
For an additional comparison on the (B − V) to TEFF relations, we also show the entirely model-based solution from Lejeune et al. (1998; dashed line). This solution is intermediate to ours (as well as the one in Gray 1992) and the one from Code et al. (1976) for the mid-A- to mid-F-type stars.
The median error in the temperature measurement for these stars (45 K) is lower than the median deviation to the fit, suggesting the potential for improvement. Iterating on the fit and removing outliers that lie further than 3σ gives an identical solution, but reduces the number of points used from 39 to 33. However, it does not improve the error of the fit by much. The scatter in the points with a (B − V) >0.6 are clearly the cause of the ill-correlated relation, as illustrated in Figure 7.
5.1.2. (V − K)–TEFF
We also present a fit of the temperature versus (V − K) color index (Equation (9) and Figure 8), the benefit here being that (V − K) colors are less sensitive to the stellar abundances than the (B − V) colors. A solution including all stars gives a median deviation in temperature of 67 K, with only one extreme outlier, HD 162003 (+5.8 σ).19 Omitting this star, we arrive at our final solution, practically identical from the first, with a median temperature deviation of 64 K. The statistical overview for this solution can be found in Table 11, and Figure 8 illustrates the fit. We note that the solution is identical when clipping stars that lie more than 3.5σ from the fit (instead of 5-σ) and has an improved median deviation in temperature of 56 K. As expected, the temperatures for the two previously mentioned metal-poor stars, HD 6582 and HD 103095, agree exceptionally well with the temperature–(V − K) relation:
Figure 8. Data points plotted as filled circles depict the observations presented here, and open triangles are the measurements from van Belle & von Braun (2009). The 1σ errors in temperature are shown, but are typically smaller than the data point. Our solution for the temperature–(V − K) relation shown as a solid line (Equation (9)), whereas the relation from van Belle & von Braun (2009) is shown as a dashed line. For details, see Section 5.1.2 and Equation (9).
Download figure:
Standard image High-resolution image5.1.3. Spectral-type–TEFF
We next derive a useful (albeit less accurate) relation between spectral type and temperature. We do this by converting the spectral types for each star into a numerical value, following the scheme: A0, A1, A2 ... F0, F1, F2 ... G0, G1, G2, ..., K0 → 0, 1, 2, ..., 10, 11, 12, ..., 20, 21, 22, ..., 30. Again, we omit the two metal-poor stars previously mentioned and fit a fourth-order polynomial to arrive at the relation
where in this equation, the variable ST refers to the numerical value for the spectral-type index. The fit for Equation (10) has a median absolute deviation of 90 K and is plotted in Figure 9. In the range from F6 to G5, we also show the fit from the data in Table 7 from van Belle & von Braun (2009; Figure 10 is a close-up view of this range) and our results are consistent with each other.
Figure 9. Data and solution for the temperature–spectral-type relation shown as circles and a solid line, respectively. The 1σ errors in temperature are shown, but are typically smaller than the data point. The data from Table 7 in van Belle & von Braun (2009) are displayed as open triangles. For details, see Section 5.1.3 and Equation (10).
Download figure:
Standard image High-resolution image5.2. Comparison to Indirectly Determined Temperatures
In the literature, three surveys exist of nearby stars that include objects that overlap with the majority of stars in this sample: Allende Prieto & Lambert (1999), Holmberg et al. (2007), and Takeda (2007). The number of stars in common with each survey respectively are 37, 34, and 25. We compare our results to these works in this section.
Figure 10. Zoomed-in version of Figure 9, showing the region that overlaps with the solution presented in van Belle & von Braun (2009). Our data and solution for the temperature–spectral-type relation are shown as circles and a solid line, respectively. The 1σ errors in temperature are shown, but are typically smaller than the data point. The data from Table 7 in van Belle & von Braun (2009) are displayed as open triangles. For details, see Section 5.1.3 and Equation (10).
Download figure:
Standard image High-resolution imageAllende Prieto & Lambert (1999, hereafter APL99) derive fundamental parameters for the stars in their survey by fitting model evolutionary tracks from Bertelli et al. (1994) to observed (B − V) photometry and absolute V-band magnitude MV. The Geneva–Copenhagen survey of the solar neighborhood II, done by Holmberg et al. (2007, hereafter GCS07), utilizes the Padova models (Girardi et al. 2000; Salasnich et al. 2000) to derive the stellar parameters based on Strömgren uvby calibrations to TEFF and MV. Last, Takeda (2007, hereafter Tak07) use the Yonsei–Yale (Y2) stellar isochrones (Yi et al. 2001; Kim et al. 2002; Yi et al. 2003; Demarque et al. 2004) to fit their spectroscopically determined TEFF along with the photometrically derived L (from the absolute magnitude and bolometric correction; see Takeda et al. 2005 for details). GCS07 demonstrate that these model isochrones (among others) show minimal differences when compared to each other, also seen in Boyajian et al. (2008). However, we choose to compare all three sources since the target overlap is not identical or complete with respect to our own, as well as the fact that different data sets and photometric indices were used for each group.
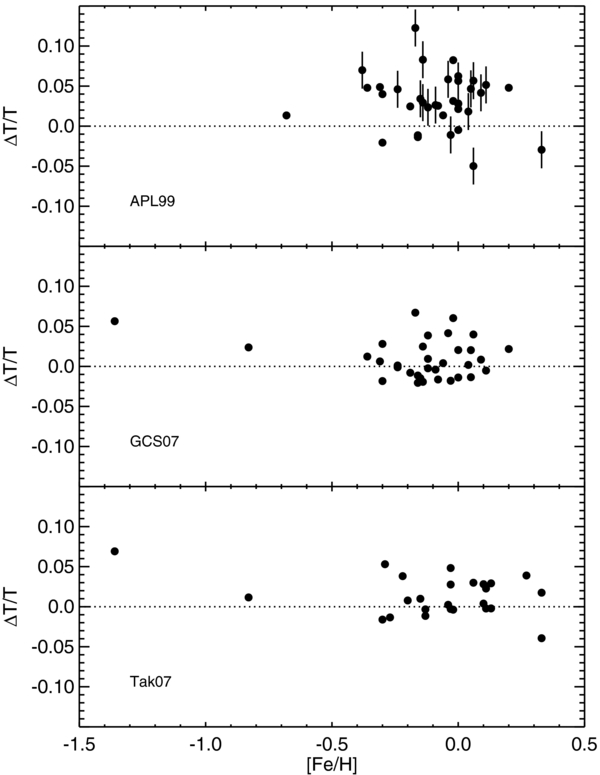
In Figure 11, we compare our temperatures to the temperatures of the stars in common in each reference. The most apparent discrepancies appear when comparing our results to those in APL99. For most cases seen here, APL99 overestimate the effective temperature of the star through the entire range of effective temperatures by about 5%, up to 15%. GCS07 and Tak07 are less drastic in comparison, but there is still a tendency of the models to overestimate the temperatures by a couple percent. Figures 12 and 13 plot the fractional offset of the stellar temperature from each method versus (B − V) color index and metallicity. For the hottest/bluest of stars (TEFF > 6500, B − V < 0.4, a range mostly covered by APL99 only), a positive offset is seen for all but one measurement. Likewise, temperatures of stars with the lowest metallicity are also overestimated in each reference compared to the temperatures presented here, but no trend can be identified with the sparse quantity of data available in this range.
Figure 11. Data plotted show the dependence on the measured temperature vs. the fractional differences between model temperatures determined by Allende Prieto & Lambert (1999, APL99), Holmberg et al. (2007, GCS07), and Takeda (2007, Tak07) and the empirical values determined in this project, along with 1σ errors for each. The dotted line marks a zero deviation between each source.
Download figure:
Standard image High-resolution imageFigure 12. Data plotted show the dependence on the (B − V) color index vs. the fractional differences between model temperatures determined by Allende Prieto & Lambert (1999, APL99), Holmberg et al. (2007, GCS07), and Takeda (2007, Tak07) and the empirical values determined in this project, along with 1σ errors for each. The dotted line marks a zero deviation between each source.
Download figure:
Standard image High-resolution imageFigure 13. Data plotted show the dependence on the metallicity vs. the fractional differences between model temperatures determined by Allende Prieto & Lambert (1999, APL99), Holmberg et al. (2007, GCS07), and Takeda (2007, Tak07) and the empirical values determined in this project, along with 1σ errors for each. The dotted line marks a zero deviation between each source.
Download figure:
Standard image High-resolution imageThe stars with the largest offsets in the effective temperatures of GCS07 are HD 103095 (5.5%), HD 146233 (5.8%) and HD 162003 (6.4%). Interestingly enough, these stars also have high discrepancies between their SED diameter and the limb-darkened diameter measured with CHARA. However, stars such as HD 10780 and HD 109358 also have high deviation in the SED diameter versus the limb-darkened diameter measured by CHARA, but their agreement with the temperature from GCS07 is at the ∼1% level. It is interesting to note that the star HD 146233 (18 Sco), which was first identified by Porto de Mello & da Silva (1997) to be a solar twin, is one of these stars with a large offset in effective temperature.
The agreement in temperature with Tak07 is better than both the APL99 and GCS07 surveys, but there is still a preference to higher temperatures than what we measure. The largest outliers in temperature offsets compared to Tak07 are HD 103095 (6.6%) and HD 128167 (5.2%). Comparing these outliers to the GCS07 outliers, there are no two stars in each that show large deviations from the model versus CHARA temperature, with the exception of the very metal poor star, HD 103095. Again, it does not appear that a star's metallicity or color index is related to the deviation in temperatures of each source.
5.3. Isochrone Masses and Ages
We determine an estimate of the stellar mass and age by fitting our temperatures and luminosities presented in Section 4.2 to the Y2 stellar isochrones (Yi et al. 2001; Kim et al. 2002; Yi et al. 2003; Demarque et al. 2004). We are able to do this for most stars observed for this work, but unfortunately, useful results are not obtainable when fitting isochrones to stars with L < 0.75 L☉, because sensitivity to age in this region is minimal.20 To run the model isochrones, input estimates are required for the abundance of iron [Fe/H] (Table 1) and α elements [α/Fe].21 For each star, isochrones were generated in increments of 0.1 Gyr, in the range of 0.1–15 Gyr. We fit the model isochrones in the theoretical temperature–luminosity plane, where the solutions from the model are purely from the theory of stellar structure. This eliminates any dependence of the color table used in transforming the model isochrone temperature to observed photometric colors (Lejeune et al. 1998). Once a best-fit isochrone is established, an age along with the associated mass for this best-fit isochrone is recorded for each star. We show an example of this routine in Figure 14, and the results are listed in Table 12.
Figure 14. Stellar isochrones generated for HD 142860. The asterisk depicts best age fit to our data and is plotted as a solid line. The luminosity and temperature and the 1σ errors for this star are also plotted. These measurement errors show that the error in the x-direction (temperature) is the least constrained input for the isochrone fit.
Download figure:
Standard image High-resolution imageTable 12. Y2 Model Isochrone Results for Stars with L > 0.75 L☉
| Star | Mass ± σ | Age ± σ |
|---|---|---|
| HD | (M☉) | (Gyr) |
| 4614 | 0.972 ± 0.012 | 5.4 ± 0.9 |
| 5015 | 1.182 ± 0.011 | 5.4 ± 0.3 |
| 16895 | 1.138 ± 0.010 | 4.0 ± 0.4 |
| 19373 | 1.169 ± 0.013 | 4.8 ± 0.5 |
| 20630 | 1.037 ± 0.042 | 0.2 ± 3.1 |
| 22484 | 1.139 ± 0.016 | 5.7 ± 0.4 |
| 30652 | 1.283 ± 0.006 | 1.3 ± 0.2 |
| 34411 | 1.041 ± 0.015 | 8.1 ± 0.8 |
| 39587 | 1.029 ± 0.029 | 2.0 ± 1.8 |
| 48737 | 1.706 ± 0.012 | 1.7 ± 0.1 |
| 56537 | 2.111 ± 0.010 | 0.8 ± 0.0 |
| 58946 | 1.355 ± 0.013 | 2.1 ± 0.2 |
| 81937 | 1.824 ± 0.016 | 1.4 ± 0.1 |
| 82328 | 1.506 ± 0.095 | 2.4 ± 0.7 |
| 82885 | 0.910 ± 0.020 | 10.6 ± 2.2 |
| 86728 | 1.034 ± 0.036 | 8.5 ± 1.8 |
| 90839 | 1.119 ± 0.035 | 1.5 ± 1.4 |
| 97603 | 2.061 ± 0.006 | 0.8 ± 0.0 |
| 102870 | 1.324 ± 0.005 | 3.3 ± 0.1 |
| 109358 | 0.852 ± 0.023 | 14.2 ± 2.1 |
| 114710 | 1.045 ± 0.013 | 4.6 ± 0.9 |
| 118098 | 1.940 ± 0.006 | 0.7 ± 0.0 |
| 126660 | 1.232 ± 0.058 | 4.2 ± 0.8 |
| 128167 | 1.194 ± 0.013 | 3.1 ± 0.4 |
| 141795 | 1.820 ± 0.026 | 0.5 ± 0.2 |
| 142860 | 1.184 ± 0.012 | 3.9 ± 0.3 |
| 146233 | 0.887 ± 0.019 | 14.9 ± 2.0 |
| 162003 | 1.311 ± 0.016 | 3.8 ± 0.1 |
| 164259 | 1.429 ± 0.013 | 2.4 ± 0.2 |
| 173667 | 1.422 ± 0.009 | 2.6 ± 0.1 |
| 177724 | 1.984 ± 0.006 | 0.8 ± 0.0 |
| 182572 | 1.186 ± 0.015 | 4.5 ± 0.8 |
| 185395 | 1.342 ± 0.011 | 2.8 ± 0.2 |
| 210418 | 1.858 ± 0.024 | 1.1 ± 0.1 |
| 213558 | 2.209 ± 0.037 | 0.4 ± 0.1 |
| 215648 | 1.192 ± 0.011 | 4.8 ± 0.2 |
| 222368 | 1.268 ± 0.009 | 3.4 ± 0.2 |
Notes. Isochrones are not sensitive to stars with L < 0.75 L☉ which includes these stars in our survey: HD 6582, HD 10780, HD 101501, HD 103095, HD 131156, and HD 185144. Errors are calculated assuming the 1σ errors on temperature and luminosity. Refer to Section 5.3 for details.
Download table as: ASCIITypeset image
We calculate the errors on the best-fit isochrone mass and age using the 1σ temperature and luminosity maximum offset for the isochrone solution. It is worth noting that the metallicity input for the model isochrones has an impact on the derived age (and in turn also on the derived mass). Lower metallicity isochrones shift down and to the left on these diagrams, so for a star with a true metallicity less than the input value, a higher isochrone age would be found. The opposite is true for stars with higher values of metallicity, where a younger age would result. For our isochrone fits, we adopt fixed values of metallicity measured from a uniform source (in this case Holmberg et al. 2007) that are used in the model input for computations. Thus, relative ages may be correct while absolute ages are highly uncertain.22
5.4. Gravity Masses
With the linear radii known for all stars in the CHARA sample, we are able to determine the mass of a star using log g estimates published in APL99 and Tak07 using the relation
where G is the gravitational constant, M* is the mass of the star, R* is the radius of the star, and g* is the surface gravity of the star. Hereafter, we will refer to the mass derived in this manner as Mg–R.
5.5. Comparative Analysis
Masses derived from isochrone fitting (MIso) and those obtainable when the surface gravity and radius are known through Equation (10) (Mg–R) are compared in Figure 15 for the stars with gravity measurements published by APL99 and Tak07. There is significant scatter; however, we find that for stars greater than ∼1.3 M☉, the masses are overpredicted when using gravities from APL99. It is possible that the offset links back to the temperature offsets discussed in the previous section. For instance, if the model temperature used to fit the spectral lines to determine log g values for the stars is offset, this will in turn lead to spurious values of log g. Presumably, these overestimated temperatures will lead to a slightly more massive star because hotter stars on the main sequence are more massive than their cooler counterparts. Sure enough, this trend can be seen in Figure 16 when comparing the deviation in temperatures and masses for these stars. Ages derived are also affected in the sense that the stars will appear younger if their temperature or log g is artificially offset to higher values. In fact, a slight trend may be seen in Figure 17 to support this when comparing our ages to the ages in GCS07 and Tak07 (APL99 did not publish ages), where our ages are typically greater.
Figure 15. Masses derived from the Y2 isochrones MIso compared to masses of stars calculated from the combination of log g estimates and our CHARA radii Mg-R. References for log g data for stars in common with the APL99 and Tak07 surveys are depicted in green and blue, respectively. The dotted line shows a 1:1 relation.
Download figure:
Standard image High-resolution imageFigure 16. Fractional deviation of the masses derived from isochrone fitting and the ones derived when using APL99 log g in combination with CHARA radius measurements vs. the fractional offset of our measured temperature vs. the ones in APL99. The dotted lines indicate zero deviation.
Download figure:
Standard image High-resolution imageFigure 17. Ages derived from the Y2 isochrones compared to ages of stars in common with GCS07 (red) and Tak07 (blue). The dotted line shows a 1:1 relation.
Download figure:
Standard image High-resolution imageThe discussion in Holmberg et al. (2007) also gives several examples of how an offset in effective temperature will, in turn, offset the metallicity and argues that these effects double up when determining the ages of the stars, thereby producing false age–metallicity relations.
For further comparison, we introduce the data set presented in Andersen (1991). Andersen (1991) provides a compilation of data on all non-interacting eclipsing binaries (EB) known at the time—a total of 90 stars, most of which are on the main sequence. Section 4 in Andersen (1991) argues that the motivation for compiling the EB data is to aid in the prediction of single-star properties where masses and radii are unobtainable by direct measurements for a large number of stars. We use these data for eclipsing binaries to compare with our results for single stars in this section.
In Figure 18, we show the relation between (B − V) color index and stellar mass. The mass–luminosity relation is shown in Figure 19. EB data from Andersen (1991) are plotted as well as the masses for stars in this project derived from the Y2 isochrones, and masses derived from the combination of the CHARA radii and log g estimates from each source (APL99 or Tak07).
Figure 18. Mass vs. color index for eclipsing binaries (black open circles) plotted with masses derived from our sample using the Y2 isochrones (black filled circles). Also plotted are the calculated Mg–R for stars in common with the APL99 (green filled circles), and Tak07 (blue filled circles) surveys.
Download figure:
Standard image High-resolution imageFigure 19. Mass vs. luminosity for eclipsing binaries (black open circles) plotted with masses derived from our sample using the Y2 isochrones (black filled circles). Also plotted are the calculated Mg-R for stars in common with the APL99 (green filled circles) and Tak07 (blue filled circles) surveys. The dotted line is the relation L∝M3.8.
Download figure:
Standard image High-resolution imageThe Y2 masses we found are in excellent agreement with the sample of EB from Andersen (1991) with respect to (B − V) color index and luminosity (Figures 18 and 19). However, comparing the Mg–R data points to the EB sample, we see that these masses are biased to larger masses, forcing them to appear underluminous compared to the EB sample as well as the Y2 data points. The effect is again most apparent in the range where the APL99 gravities are used, where the systematics appear for stars with masses greater than ∼1.3 M☉.
6. SUMMARY AND CONCLUSION
In this paper, we present the angular diameters of nearby, main-sequence stars measured with the CHARA Array. The survey includes a total of 44 stars for which the angular diameter is measured to better than 4%. Robust bolometric flux measurements of the stars are presented, yielding absolute luminosities and effective temperatures measured to accuracies on the average of 1.8% and 1%, respectively. Lastly, we extract masses and ages of the stars by applying the Y2 model isochrones to our data
We show that published values of such stellar parameters derived indirectly are not consistent with our results. Our data compared to the published values show that several sources overestimate the effective temperature by 1.5%–4%. The values for modeled stellar radius compensate this offset by being underestimated in order for the luminosity to come out right. Generally speaking, this offset is most apparent in the metal-poor stars as well as the earlier-type stars (≳ 1.3 M☉) that we observed. We propose that this preference for models to derive hotter temperatures is the cause for further divergence in a star's surface gravity measurements, which consequently yields higher masses and younger ages. Excellent agreement is seen when comparing our data to a large sample of EBs.
This data sample is used to solve for empirically based temperature relations for A-, F-, and G-type main-sequence stars, with precision close to the 1% level on the color–temperature calibrations. The results of the B − V color–temperature relation are consistent with other relations for the stars redder than B − V ∼ 0.4 (mid-F- through G-type). However, for stars earlier than this (the A- and early F-types), our solution is a couple hundred Kelvin cooler than all but one of the relations we use for comparison. This is likely due to the sparsity of good-quality empirical data used for fitting in this region. Our data is better correlated in the V − K color–temperature relation than the interferometric data in van Belle & von Braun (2009) for the F- and G-type stars, due to the high precision of our measurements compared to theirs, but the fits to the data are indistinguishable in this range. For the earlier-type stars, moderate disagreement is still present, again from lack of complete sampling in this region.
Ongoing observations of more nearby main-sequence stars are under way by our group at the CHARA Array. Color–temperature calibrations with various other color indices will be implemented in the forthcoming papers in the series. Stellar metallicity was ignored in this work; however, including it in temperature relations will almost certainly beat the errors down even more than what we have achieved with the current fit. In our future efforts, we aim to populate the data set enough to identify accurate color–temperature–metallicity relations as well as extend the sample down to the lower end of the main sequence.
T.S.B. acknowledges support provided by NASA through Hubble Fellowship grant No. HST-HF-51252.01 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555. The CHARA Array is funded by the National Science Foundation through NSF grant AST-0908253 and by Georgia State University through the College of Arts and Sciences. This research has made use of the SIMBAD literature database, operated at CDS, Strasbourg, France, and of NASA's Astrophysics Data System. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by NASA and NSF.
Footnotes
- 7
The average precision of these angular diameter determinations depended primarily on the brightness of the object and was ≈6.5% for the 32 stars measured.
- 8
Very conservative limits for observing with the CHARA Classic beam combiner require V < 10 mag and K < 7 mag.
- 9
This sequence of calibrator–object–calibrator is called a "bracket."
- 10
- 11
- 12
All have θSED < 0.66 mas, with a mean angular diameter error of 4.4%.
- 13
The formal limits to detection of companions with our instrument is currently unknown, but is thought to be sensitive to binaries with ΔK ≲ 2.5 (D. Raghavan 2009, private communication).
- 14
Toyota et al. (2009) comment that the Vr trend is not attributed to the visual companion, HD 162004 ∼30'' away.
- 15
Which coincidentally has been assigned the name Chara (Hoffleit & Jaschek 1991).
- 16
Distance of the furthest star is ∼30 pc.
- 17
There are two stars, HD 6582 and HD 103095, with metallicity [Fe/H] <−0.75.
- 18
A fit to our data with a power relation yields an initial solution with a median deviation in temperature of 125 K, and 101 K removing the points with low metallicity. A deviation of 92 K is found after removing outliers lying more than 3σ from the fit, almost double the value we find for the polynomial fit.
- 19
We note that this star has a visual companion HD 162004, and thus could have bad photometry. Note that HD 162003 was an outlier in the B − V relation, with a negative offset from the fit derived.
- 20
Stars within this range are HD 6582, HD 10780, HD 101501, HD 103095, HD 131156, and HD 185144.
- 21
The [α/Fe] for all stars are zero (Carney 1996). We assign [Fe/H] = 0 for HD 56537, HD 141795, and HD 213558 because no metallicity measurements are available in the literature for these stars.
- 22
A characteristic error introduced by a 0.1 dex uncertainty in the metallicity may introduce errors ranging from about 0.1 to 2.0 Gyr and 0.06 M☉ for the A- to G-type stars, respectively.
- Absil O., di Folco E., Mérand A. et al. 2008 A&A 487 1041
- Abt H. A. and Levy S. G. 1976 ApJS 30 273
- Allen D. A. and Cragg T. A. 1983 MNRAS 203 777
- Allende Prieto C. and Lambert D. L. 1999 A&A 352 555
- Alonso A., Arribas S. and Martinez-Roger C. 1994 A&AS 107 365
- Andersen J. 1991 A&AR 3 91
- Argue A. N. 1963 MNRAS 125 557
- Argue A. N. 1966 MNRAS 133 475
- Arp H. C. 1958 AJ 63 118
- Arribas S. and Martinez Roger C. 1987 A&AS 70 303
- Arribas S. and Martinez Roger C. 1989 A&A 215 305
- Aumann H. H. and Probst R. G. 1991 ApJ 368 264
- Baines E. K., McAlister H. A., ten Brummelaar T. A. et al. 2008 ApJ 680 728
- Barnes T. G., Evans D. S. and Moffett T. J. 1978 MNRAS 183 285
- Barry D. C. 1969 PASP 81 339
- Baruch J. E. F., Griffiths W. K., Nittmann J. et al. 1983 MNRAS 202 691
- Behr B. B., Hajian A. R., Cenko A. T. et al. 2009 ApJ 705 543
- Bergeat J. and Lunel M. 1980 A&A 87 139
- Berger D. H., Gies D. R., McAlister H. A. et al. 2006 ApJ 644 475
- Berriman G., de Campli W. M., Werner M. W. and Hatchett S. P. 1983 MNRAS 205 859
- Bertelli G., Bressan A., Chiosi C., Fagotto F. and Nasi E. 1994 A&AS 106 275
- Blackwell D. E., Petford A. D., Arribas S., Haddock D. J. and Selby M. J. 1990 A&A 232 396
- Blackwell D. E. and Shallis M. J. 1977 MNRAS 180 177
- Blackwell D. E., Shallis M. J. and Selby M. J. 1979 MNRAS 188 847
- Bok B. J., Bok P. F. and Miller E. W. 1972 AJ 77 733
- Bond H. E. 1970 ApJS 22 117
- Booth A. J. 1997 IAU Symp. 189 ed T. R. Bedding, A. J. Booth and J. Davis (Cambridge: Cambridge Univ. Press) 147
- Bouigue R. 1959 Ann. Obs. Astron. Meteo. Toulouse 27 47
- Bowsher E. C., McAlister H. A. and Ten Brummelaar T. A. 2010 Proc. SPIE 7734 92
- Boyajian T. S., McAlister H. A., Baines E. K. et al. 2008 ApJ 683 424
- Boyajian T. S., McAlister H. A., Cantrell J. R. et al. 2009 ApJ 691 1243
- Breger M. 1974 ApJ 188 53
- Caillault J.-P. and Patterson J. 1990 AJ 100 825
- Cameron R. C. 1966 Georgetown Obs. Monogram 21 0
- Campins H., Rieke G. H. and Lebofsky M. J. 1985 AJ 90 896
- Cardelli J. A., Clayton G. C. and Mathis J. S. 1989 ApJ 345 245
- Carney B. W. 1996 PASP 108 900
- Carney B. W. 1979 ApJ 233 211
- Carney B. W. 1983a AJ 88 623
- Carney B. W. 1983b AJ 88 610
- Carney B. W. and Aaronson M. 1979 AJ 84 867
- Carter B. S. 1990 MNRAS 242 1
- Casagrande L., Ramírez I., Meléndez J., Bessell M. and Asplund M. 2010 A&A 512 A54
- Celis S. L. 1975 A&AS 22 9
- Claret A. 2000 A&A 363 1081
- Code A. D., Bless R. C., Davis J. and Brown R. H. 1976 ApJ 203 417
- Cohen M., Wheaton W. A. and Megeath S. T. 2003 AJ 126 1090
- Colina L., Bohlin R. and Castelli F. 1996 AJ 112 307
- Cousins A. W. J. 1963 Mon. Notes Astron. Soc. South. Afr. 22 12
- Cousins A. W. J. 1964 Mon. Notes Astron. Soc. South. Afr. 23 175
- Cousins A. W. J. 1984 S. Afr. Astron. Obs. Circ. 8 59
- Cousins A. W. J. and Stoy R. H. 1962 R. Greenwich Obs. Bull. 64 103
- Cowley A. P., Hiltner W. A. and Witt A. N. 1967 AJ 72 1334
- 2000 Allen's Astrophysical Quantities 4th ed. ed A. N. Cox (New York: AIP)
- Crawford D. L. 1975 AJ 80 955
- Crawford D. L. and Barnes J. V. 1969 AJ 74 407
- Crawford D. L. and Barnes J. V. 1970 AJ 75 978
- Crawford D. L., Barnes J. V., Faure B. Q. and Golson J. C. 1966 AJ 71 709
- Crawford D. L., Barnes J. V., Gibson J. et al. 1972 A&AS 5 109
- Crawford D. L. and Perry C. L. 1989 PASP 101 601
- Cutri R. M., Skrutskie M. F., van Dyk S. et al. 2003 The 2MASS All Sky Catalog of Point Sources (Pasadena, CA: IPAC)
- Danziger I. J. and Dickens R. J. 1967 ApJ 149 55
- Davis J. 1985 Calibration of Fundamental Stellar Quantities ed D. S. Hayes, L. E. Pasinetti and A. G. D. Philip (Cambridge: Cambridge Univ. Press) 193
- Davis J. 1997 Fundamental Stellar Properties: The Interaction between Observation and Theory ed T. R. Bedding, A. J. Booth and J. Davis (Cambridge: Cambridge Univ. Press) 31
- Demarque P., Woo J.-H., Kim Y.-C. and Yi S. K. 2004 ApJS 155 667
- de Vaucouleurs G. 1959 Planet. Space Sci. 2 26
- Dyck H. M., Benson J. A., van Belle G. T. and Ridgway S. T. 1996 AJ 111 1705
- Elias J. H., Frogel J. A., Matthews K. and Neugebauer G. 1982 AJ 87 1029
- Elliott J. E. 1974 AJ 79 1082
- Fabregat J. and Reglero V. 1990 A&AS 82 531
- Feinstein A. 1974 AJ 79 1290
- Fernie J. D. 1969 J. R. Astron. Soc. Can. 63 133
- Fernie J. D., Hagen J. P. Jr., Hagen G. L. and McClure L. 1971 PASP 83 79
- Fitch W. S. 1955 ApJ 121 690
- Frank J., King A. R., Sherrington M. R., Jameson R. F. and Axon D. J. 1981 MNRAS 195 505
- Frogel J. A., Persson S. E., Matthews K. and Aaronson M. 1978 ApJ 220 75
- Gascoigne S. C. B. 1962 MNRAS 124 201
- Gehrz R. D. and Woolf N. J. 1970 ApJ 161 L213
- Ghosh S. K., Iyengar K. V. K., Tandon S. N. et al. 1984 MNRAS 206 611
- Girardi L., Bressan A., Bertelli G. and Chiosi C. 2000 A&AS 141 371
- Glass I. S. 1974 Mon. Notes Astron. Soc. South. Afr. 33 53
- Glass I. S. 1975 MNRAS 171 19P
- Grant G. 1959 ApJ 129 62
- 1992 The Observation and Analysis of Stellar Photospheres ed D. F. Gray (Cambridge: Cambridge Univ. Press) 470
- Gray R. O. 1998 AJ 116 482
- Gray R. O., Corbally C. J., Garrison R. F., McFadden M. T. and Robinson P. E. 2003 AJ 126 2048
- Gray R. O., Corbally C. J., Garrison R. F. et al. 2006 AJ 132 161
- Gray R. O., Napier M. G. and Winkler L. I. 2001 AJ 121 2148
- Gray R. O. and Olsen E. H. 1991 A&AS 87 541
- Grønbech B. and Olsen E. H. 1976 A&AS 25 213
- Grønbech B., Olsen E. H. and Strömgren B. 1976 A&AS 26 155
- Guetter H. H. 1977 AJ 82 598
- Guetter H. H. 1979 AJ 84 1846
- Gutierrez-Moreno A. and Moreno H. 1968 ApJS 15 459
- Gutierrez-Moreno A. et al. 1966 Publ. Dept. Astron. Univ. Chile 1 1
- Haas M. and Leinert C. 1990 A&A 230 87
- Häggkvist L. and Oja T. 1966 Ark. Astron. 4 137
- Häggkvist L. and Oja T. 1969 Ark. Astron. 5 303
- Haggkvist L. and Oja T. 1970 private communication
- Han I. and Gatewood G. 2002 PASP 114 224
- Hanbury Brown R., Davis J. and Allen L. R. 1974a MNRAS 167 121
- Hanbury Brown R. H., Davis J., Lake R. J. W. and Thompson R. J. 1974b MNRAS 167 475
- Harris D. L. III and Upgren A. R. 1964 ApJ 140 151
- Hauck B. and Mermilliod M. 1998 A&AS 129 431
- Henry J. P., Becklin E. E. and Telesco C. M. 1984 ApJ 280 98
- 1991 The Bright Star Catalogue ed D. Hoffleit and C. Jaschek (New Haven, CT: Yale Univ. Observatory)
- Hogg A. R. 1958 Mount Stromlo Obs. Mimeographs 2 1
- Holmberg J., Nordström B. and Andersen J. 2007 A&A 475 519
- Holmberg J., Nordström B. and Andersen J. 2008 A&A 501 941
- Imagawa F. 1967 Mem. Coll. Sci. Kyoto Imp. Univ. 31 93
- Iriarte B., Johnson H. L., Mitchell R. I. and Wisniewski W. K. 1965 S&T 30 21
- Irvine W. M., Simon T., Menzel D. H., Pikoos C. and Young A. T. 1968a AJ 73 807
- Irvine W. M., Simon T., Menzel D. H. et al. 1968b AJ 73 251
- Irwin J. B. 1961 ApJS 6 253
- Jennens P. A. and Helfer H. L. 1975 MNRAS 172 667
- Jerzykiewicz M. and Serkowski K. 1966 PASP 78 546
- Johansen K. T. and Gyldenkerne K. 1970 A&AS 1 165
- Johnson H. L. 1953 ApJ 117 361
- Johnson H. L. 1964 Bol. Obs. Tonantzintla Tacubaya 3 305
- Johnson H. L. 1965a ApJ 141 170
- Johnson H. L. 1965b Commun. Lunar Planet. Lab. 3 73
- Johnson H. L. 1968 Interstellar Extinction ed B. M. Middlehurst and L. H. Aller (Chicago, IL: Univ. Chicago Press) 167
- Johnson H. L. and Harris D. L. 1954 ApJ 120 196
- Johnson H. L. and Knuckles C. F. 1957 ApJ 126 113
- Johnson H. L., MacArthur J. W. and Mitchell R. I. 1968 ApJ 152 465
- Johnson H. L., Mitchell R. I., Iriarte B. and Wisniewski W. Z. 1966 Commun. Lunar Planet. Lab. 4 99
- Johnson H. L. and Morgan W. W. 1953 ApJ 117 313
- Jones R. V., Carney B. W. and Latham D. W. 1988 ApJ 332 206
- Kenyon S. J. 1988 AJ 96 337
- Kenyon S. J. and Gallagher J. S. 1983 AJ 88 666
- Kilkenny D. and Menzies J. W. 1986 MNRAS 222 373
- Kim Y.-C., Demarque P., Yi S. K. and Alexander D. R. 2002 ApJS 143 499
- Konacki M. 2005 ApJ 626 431
- Kostjuk N. D. 2004 VizieR Online Data Catalog 4027 0
- Kozok J. R. 1985 A&AS 61 387
- Lake R. 1962 Mon. Notes Astron. Soc. South. Afr. 21 191
- Lake R. 1964 Mon. Notes Astron. Soc. South. Afr. 23 14
- Leggett S. K., Bartholomew M., Mountain C. M. and Selby M. J. 1986 MNRAS 223 443
- Leitherer C., Hefele H., Stahl O. and Wolf B. 1982 A&A 108 102
- Leitherer C. and Wolf B. 1984 A&A 132 151
- Lejeune T., Cuisinier F. and Buser R. 1998 A&AS 130 65
- Little-Marenin I. R., Simon T., Ayres T. R. et al. 1986 ApJ 303 780
- Ljunggren B. and Oja T. 1965 Ark. Astron. 3 439
- Lonsdale C. J., Becklin E. E., Lee T. J. and Stewart J. M. 1982 AJ 87 1819
- Lutz T. E. 1971 PASP 83 488
- Markwardt C. B. 2009 Astronomical Data Analysis Software and Systems XVIII ed D. A. Bohlender, D. Durand and P. Dowler (San Francisco, CA: ASP) 251
- Marlborough J. M. 1964 AJ 69 215
- McCarthy D. W. Jr. 1984 AJ 89 433
- McClure R. D. 1970 AJ 75 41
- Mechler G. E. 1976 AJ 81 107
- Mechler G. E. and McGinnis S. K. 1978 AJ 83 1646
- Mendoza E. E., Gomez V. T. and Gonzalez S. 1978 AJ 83 606
- Mendoza E. E. and Gonzalez S. F. 1974 RevMexAA 1 67
- Mermilliod J.-C. 1986 Catalogue of Eggen's UBV Data 0
- Mermilliod J. C. 1997 VizieR Online Data Catalog 2168 0
- Miczaika G. R. 1954 AJ 59 233
- Mitchell R. I. and Schuster W. J. 1985 AJ 90 2116
- Moffett T. J. and Barnes T. G. III. 1979 PASP 91 180
- Morbey C. L. and Griffin R. F. 1987 ApJ 317 343
- Moreno H. 1971 A&A 12 442
- Nakagiri M. and Yamashita Y. 1979 Ann. Tokyo Astron. Obs. 17 221
- Naur P. 1955 ApJ 122 182
- Neckel H. 1974 A&AS 18 169
- Neugebauer G. and Leighton R. B. 1969 Two-micron Sky Survey: A Preliminary Catalogue (Washington, DC: NASA)
- Nicolet B. 1978 A&AS 34 1
- Niconov V. B., Nekrasova S. V., Polosuina N. S., Rachkouvsky N. D. and Chuvajev W. K. 1957 Izv. Ordena Trudovogo Krasnogo Znameni Krym. Astrofiz. Obs. 17 42
- Nidever D. L., Marcy G. W., Butler R. P., Fischer D. A. and Vogt S. S. 2002 ApJS 141 503
- Nikrasova V., Nikonov V. B., Polosukhina N. S. and Rybka E. 1962 Izv. Ordena Trudovogo Krasnogo Znameni Krym. Astrofiz. Obs. 27 228
- O'Connell D. J. K. 1964 Ric. Astron. 6 523
- Oja T. 1963 Ark. Astron. 3 273
- Oja T. 1970 private communication
- Oja T. 1983 A&AS 52 131
- Oja T. 1984 A&AS 57 357
- Oja T. 1985a A&AS 61 331
- Oja T. 1985b A&AS 59 461
- Oja T. 1986 A&AS 65 405
- Olsen E. H. 1977 A&AS 29 313
- Olsen E. H. 1983 A&AS 54 55
- Olsen E. H. 1993 A&AS 102 89
- Olsen E. H. 1994a A&AS 104 429
- Olsen E. H. 1994b A&AS 106 257
- Olson E. C. 1974 AJ 79 1424
- Penston M. J. 1973 MNRAS 164 133
- Perry C. L. 1969 AJ 74 139
- Pfleiderer J., Dachs J. and Haug U. 1966 Z. Astrophys. 64 116
- Philip A. G. D. and Philip K. D. 1973 ApJ 179 855
- Pickles A. J. 1998 PASP 110 863
- Piirola V. 1976 Observatory and Astrophysics Laboratory University of Helsinki Report 1 0
- Porto de Mello G. F. and da Silva L. 1997 ApJ 482 L89
- Rakos K. D., Albrecht R., Jenkner H. et al. 1982 A&AS 47 221
- Reglero V. and Fabregat J. 1991 A&AS 90 25
- Reglero V., Gimenez A., de Castro E. and Fernandez-Figueroa M. J. 1987 A&AS 71 421
- Richichi A., Percheron I. and Khristoforova M. 2005 A&A 431 773
- Roman N. G. 1955 ApJS 2 195
- Royer F., Zorec J. and Gomez A. E. 2006 VizieR Online Data Catalog 346 30671
- Rucinski S. M. 1983 IBVS 2277 1
- Rufener F. 1976 A&AS 26 275
- 1961 XIth General Assembly—Transactions of the IAU ed D. H. Sadler (Berkeley, CA: IAU) Vol. XI B
- Salasnich B., Girardi L., Weiss A. and Chiosi C. 2000 A&A 361 1023
- Sanwal N. B., Parthasarathy M. and Abhyankar K. D. 1973 Observatory 93 30
- Schild R. E. 1973 AJ 78 37
- Schmidt E. G. 1971 ApJ 165 335
- Schuster W. J. and Nissen P. E. 1988 A&AS 73 225
- Selby M. J., Hepburn I., Blackwell D. E. et al. 1988 A&AS 74 127
- Serkowski K. 1961 Lowell Obs. Bull. 5 157
- Shao C. Y. 1964 AJ 69 858
- Sharpless S. 1952 ApJ 116 251
- Sjögren U. 1964 Ark. Astron. 3 339
- Sowell J. R. and Wilson J. W. 1993 PASP 105 36
- Stetson P. B. 1991 AJ 102 589
- Stokes N. R. 1972a MNRAS 159 165
- Stokes N. R. 1972b MNRAS 160 155
- Szabados L. 1981 Commun. Konkoly Obs. Hungary 77 1
- Takeda Y. 2007 PASJ 59 335
- Takeda Y., Ohkubo M., Sato B., Kambe E. and Sadakane K. 2005 PASJ 57 27
- Taylor B. J. and Joner M. D. 1992 PASP 104 911
- Telesco C. M., Decher R. and Gatley I. 1985 ApJ 299 896
- Telesco C. M., Decher R. and Gatley I. 1986 ApJ 302 632
- Telesco C. M. and Gatley I. 1984 ApJ 284 557
- ten Brummelaar T. A., McAlister H. A., Ridgway S. T. et al. 2005 ApJ 628 453
- Tifft W. G. 1963 MNRAS 125 199
- Tolbert C. R. 1964 ApJ 139 1105
- Toyota E., Itoh Y., Ishiguma S. et al. 2009 PASJ 61 19
- van Belle G. T., Creech-Eakman M. J. and Hart A. 2009 MNRAS 394 1925
- van Belle G. T., Lane B. F., Thompson R. R. et al. 1999 AJ 117 521
- van Belle G. T. and van Belle G. 2005 PASP 117 1263
- van Belle G. T., van Belle G., Creech-Eakman M. J. et al. 2008 ApJS 176 276
- van Belle G. T. and von Braun K. 2009 ApJ 694 1085
- van den Bergh S. 1967 AJ 72 70
- van Leeuwen F. 2007 Hipparcos, the New Reduction of the Raw Data ed F. van Leeuwen (Dordrecht: Springer) Vol. 350 20
- Veeder G. J. 1974 AJ 79 1056
- Veeder G. J., Matson D. L. and Smith J. C. 1978 AJ 83 651
- Voelcker K. 1975 A&AS 22 1
- Wallerstein G. and Helfer H. L. 1961 ApJ 133 562
- Warren W. H. Jr. 1973 AJ 78 192
- Warren W. H. Jr. and Hesser J. E. 1977 ApJS 34 115
- Wenger M., Ochsenbein F., Egret D. et al. 2000 A&AS 143 9
- Yi S., Demarque P., Kim Y.-C. et al. 2001 ApJS 136 417
- Yi S. K., Kim Y.-C. and Demarque P. 2003 ApJS 144 259
- Zhao M., Monnier J. D., Pedretti E. et al. 2009 ApJ 701 209