ABSTRACT
We discuss new photometry from high-resolution images of seven intermediate-age (1–2 Gyr) star clusters in the Large Magellanic Cloud taken with the Advanced Camera for Surveys on board the Hubble Space Telescope. We fit color–magnitude diagrams (CMDs) with several different sets of theoretical isochrones and determine systematic uncertainties for population parameters when derived using any one set of isochrones. The cluster CMDs show several interesting features, including extended main-sequence turnoff (MSTO) regions, narrow red giant branches, and clear sequences of unresolved binary stars. We show that the extended MSTOs are not caused by photometric uncertainties, contamination by field stars, or the presence of binary stars. Enhanced helium abundances in a fraction of cluster stars are also ruled out as the reason for the extended MSTOs. Quantitative comparisons with simulations indicate that the MSTO regions are better described by a spread in ages than by a bimodal age distribution, although we cannot formally rule out the latter for the three lowest-mass clusters in our sample (which have masses lower than ∼3 × 104 M☉). This conclusion differs from that of some previous works which suggested that the age distribution in massive clusters in our sample is bimodal. This suggests that any secondary star formation occurred in an extended fashion rather than through short bursts. We discuss these results in the context of the nature of multiple stellar populations in star clusters.
1. INTRODUCTION
An accurate knowledge of stellar populations of "intermediate" age (≈(1–3) × 109 yr) is important within the context of several currently hot topics in astrophysics. Intermediate-age stars typically dominate the emission observed from galaxies at high redshift (e.g., van der Wel et al. 2006). Furthermore, star clusters in this age range are critical for testing predictions of the dynamical evolution of star clusters (e.g., Goudfrooij et al. 2007) and for understanding the evolution of intermediate-mass (IM) stars. The Large Magellanic Cloud (LMC) hosts a rich system of intermediate-age star clusters. The first surveys dedicated to studying properties of these clusters were based on integrated colors (e.g., Searle et al. 1980, hereafter SWB). These studies led to empirical and homogeneous age scales such as the "SWB parameter" and the "S parameter" (Elson & Fall 1985, 1988; Girardi et al. 1995; Pessev et al. 2008), which describe the position of the cluster in integrated-light color–color diagrams. While a number of more recent studies of such intermediate-age clusters have determined ages more directly by fitting the location of the main-sequence turnoff (MSTO) region with model isochrones in color–magnitude diagrams (CMDs; e.g., Bertelli et al. 2003; Kerber et al. 2007; Mucciarelli et al. 2007; Mackey et al. 2008; Milone et al. 2009), such age determinations are still rather sparse and somewhat dependent on the stellar model being used. It is therefore important to obtain more CMD-based ages and metallicities of intermediate-age clusters and to study any systematic uncertainties related to the choice of any particular stellar model and its ingredients.
Another current hot topic in astrophysics is that of multiple stellar populations in globular clusters (GCs). The standard paradigm that GCs consist of stars born at the same time out of the same material has faced serious challenges over the last decade. It is now known that the most massive GCs in our Galaxy such as ω Cen and M 54 host multiple red giant branches (RGBs) due to populations with different [Fe/H] (e.g., Sarajedini & Layden 1995; Lee et al. 1999; Hilker & Richtler 2000; Villanova et al. 2007; Carretta et al. 2010). Slightly less massive Galactic GCs such as NGC 2808, NGC 1851, and 47 Tuc show multiple sub-giant branches (SGBs) and/or multiple main sequences (MSs), which are typically interpreted as populations with different helium abundance (e.g., Piotto et al. 2007; Milone et al. 2008; Anderson et al. 2009). While lower-mass Galactic GCs typically do not show clear evidence for multiple populations from optical broadband photometry, spectroscopic surveys do show significant star-to-star abundance variations in light elements such as C, N, O, F, and Na (often dubbed "Na–O anticorrelations") within all Galactic GCs studied to date in sufficient detail (Carretta et al. 2009, and references therein). Since these abundance variations have been found among RGB stars as well as MS stars within a given GC (Gratton et al. 2004), the cause of the variations seems to be that secondary population(s) formed out of material shed by an evolved population within the cluster. While the chemical processes involved in causing the light element abundance variations have largely been identified as proton-capture reactions in hydrogen burning at high temperature (≳ 40 × 106 K; see, e.g., Gratton et al. 2004), the old age of Galactic GCs has precluded a clear picture of the timescales and hence the types of stars involved in the chemical enrichment of the second-generation stars. Currently, the most popular candidates are (1) intermediate-mass AGB (asymptotic giant branch) stars (, hereafter IM–AGB; e.g., D'Antona & Ventura 2007, and references therein), (2) rapidly rotating massive stars (often abbreviated as FRMS; e.g., Decressin et al. 2007), and (3) massive binary stars (de Mink et al. 2009).
Recently, deep CMDs from images taken with the Advanced Camera for Surveys (ACS) aboard the Hubble Space Telescope (HST) provided conclusive evidence that several massive intermediate-age star clusters in the Magellanic Clouds have extended and/or multiple MSTO regions (Mackey et al. 2008; Glatt et al. 2008; Milone et al. 2009; Goudfrooij et al. 2009, hereafter Paper I), in some cases accompanied by composite red clumps (Girardi et al. 2009; Rubele et al. 2011). To date, these properties have been interpreted in three main ways: (1) bimodal age distributions (Mackey et al. 2008; Milone et al. 2009), (2) age spreads of 200–500 Myr (Goudfrooij et al. 2009; Mackey et al. 2008; Milone et al. 2009; Girardi et al. 2009; Rubele et al. 2010), and (3) spreads in rotation velocity among turnoff stars (Bastian & de Mink 2009).
In this second paper of our series, we follow methods presented in Paper I and conduct a detailed investigation of population parameters of seven intermediate-age star clusters in the LMC. While CMDs of clusters in this sample were already presented in Mackey et al. (2008) and Milone et al. (2009), we employ different methods and present additional analysis of the clusters. At the data reduction level, this includes corrections for charge transfer inefficiency that are specifically determined for the data sets used here. At the analysis and interpretation level, we investigate the impact of unresolved binary stars associated with one and two generations of stars on the MSTO region, we use different techniques for assessing background contamination, and we investigate how well different sets of isochrones fare when compared with the observations. The additional analysis allows us to reveal new properties relevant to the assembly of these intermediate-age star clusters and their evolutionary association with multiple stellar populations in ancient Galactic GCs. In a companion paper in this series (Goudfrooij et al. 2011, hereafter Paper III), we synthesize the results from the current paper along with new radial distributions of cluster stars at different evolutionary phases and dynamical considerations to constrain the origin of extended MSTO (hereafter eMSTO) regions in intermediate-age star clusters in the LMC.
The remainder of this paper is organized as follows. Section 2 presents the observations, Section 3 discusses details of the stellar photometry and evaluates contamination by field stars. Section 4 presents our isochrone fitting analysis using different sets of theoretical isochrones. We discuss the level of helium abundance enhancement of any subpopulation of stars in these clusters in Section 5. In Section 6, we analyze the morphology of the eMSTO regions. Section 7 discusses the results in the context of the nature of multiple stellar populations in star clusters in general, and Section 8 presents our main conclusions.
2. SAMPLE SELECTION AND OBSERVATIONS
Our sample consists of seven star clusters (NGC 1751, NGC 1783, NGC 1806, NGC 1846, NGC 1987, NGC 2108, and LW431) in the LMC with an SWB parameter in the range IVb–VI, translating to ages between roughly 1.0 and 2.5 Gyr. Main properties of the clusters are listed in Table 1, along with a journal of their HST observations with the wide-field channel (WFC) of the ACS instrument as part of HST program GO-10595 (PI: P. Goudfrooij). We centered the target clusters on one of the two CCD chips of the ACS/WFC camera so that the observations cover a fairly large radial extent, enabling us to study variations of cluster properties with radius and evaluate the properties of the field star population. Three exposures were taken in each of the F435W, F555W, and F814W filters: two long exposures of 340 s each and one shorter exposure to avoid saturation of the brightest stars in the cluster (90 s, 40 s, and 8 s in F435W, F555W, and F814W, respectively). The two long exposures in each filter were spatially offset from each other by 3 011 in a direction +85
011 in a direction +85 28 with respect to the positive X-axis of the CCD array. This was done to move across the gap between the two ACS/WFC CCD chips, as well as to simplify the identification and removal of hot pixels.
28 with respect to the positive X-axis of the CCD array. This was done to move across the gap between the two ACS/WFC CCD chips, as well as to simplify the identification and removal of hot pixels.
Table 1. Main Properties of the Star Clusters Studied in this Paper
| Cluster | Obs. Date | V | Ref. | SWB |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| NGC 1751 | Oct 18–19, 2006 | 11.67 ± 0.13 | 1 | VI |
| NGC 1783 | Jan 1, 2006 | 10.39 ± 0.03 | 1 | V |
| NGC 1806 | Sep 29, 2005 | 11.00 ± 0.05 | 1 | V |
| NGC 1846 | Jan 12, 2006 | 10.68 ± 0.20 | 1 | VI |
| NGC 1987 | Oct 18, 2006 | 11.74 ± 0.09 | 1 | IVb |
| NGC 2108 | Aug 22, 2006 | 12.32 ± 0.04 | 2a | IVb |
| LW 431 | Nov 5–6, 2006 | 13.67 ± 0.04 | 2a | VI |
Notes. Column 1: name of star cluster. Column 2: date of HST/ACS observations. Column 3: integrated V magnitude. Column 4: reference of V magnitude. Reference 1: Goudfrooij et al. 2006; reference 2: Bica et al. 1996. (5): SWB type from Bica et al. (1996). aUncertainty only includes internal errors associated with measurements of cluster and one background aperture.
Download table as: ASCIITypeset image
3. ANALYSIS
3.1. Photometry
Stellar photometry was conducted using point-spread function (PSF) fitting on the flat-fielded (flt) files produced by the HST calibration pipeline, using the spatially variable "effective PSF" (ePSF) method described in Anderson & King (2000) and tailored for ACS/WFC data by Anderson & King (2006). A detailed description of the application of the ePSF method to ACS/WFC data is given in Anderson et al. (2008b, 2008a). We selected all stars with the ePSF parameter "PSF fit quality" q < 0.5 and "isolation index" of 5. The latter parameter selects stars that have no brighter neighbors within a radius of 5 pixels. To further weed out hot pixels, cosmic rays, and spurious detections along diffraction spikes, the geometrically corrected positions among the three images per filter were compared. We selected objects with coordinates matching within a tolerance of 0.2 pixels in either axis, which eliminated the hot pixels and cosmic ray hits effectively.
Corrections for imperfect charge transfer efficiency (CTE) of the ACS/WFC CCDs were made specifically for the case of photometry from flt files featuring varying exposure times following Kozhurina-Platais et al. (2007). The accuracy of our CTE corrections is such that the rms scatter of the magnitude residuals is 0.02 mag at an instrumental magnitude of −2 (corresponding to mF435W = 23.8, mF555W = 24.4, and mF814W = 23.5 in magnitude units relative to Vega). This uncertainty is smaller than the photometric measurement errors at those magnitudes.
Photometric incompleteness as functions of stellar brightness, color, and position in the cluster was quantified by repeatedly adding small numbers of artificial ePSFs to the images, covering the magnitude and color ranges found in the CMDs. The overall radial distribution of the artificial stars inserted followed that of the stars in the image. We refer the reader to Paper I for further details of our photometric methods and calibration.
3.2. Color–Magnitude Diagrams
CMDs for the star clusters in our sample were created for both mF435W versus mF435W − mF814W and mF555W versus mF555W − mF814W. CMDs for all selected stars are plotted in the left panels of Figures 1 and 2. To decrease and assess contamination by field stars, we also plot CMDs for all stars within one core radius based on fits to a single-mass King (1962) model from the cluster centers (derived as described in Section 3.3 below) in the middle panels, and CMDs for stars located in regions near the corners of the HST/ACS image, which are presumably dominated by non-cluster stars, in the right panels. The latter regions were chosen to cover the same surface area as those in the middle panels. In Figure 1 we identify and label the following evolved phases of stellar evolution: the MS, MSTO, red clump (hereafter RC5), the RGB, and the AGB.
Figure 1. mF435W vs. mF435W − mF814W CMDs for the HST/ACS images of NGC 1751, NGC 1783, and NGC 1806 (we refer to Paper I for the CMDs of NGC 1846). The left panels show all detected sources that passed our selection criteria. The middle panels show all such sources within the King core radius of the star cluster in question. The right panels show all sources detected in areas near the corners of the image furthest away from the cluster center. These composite "field" regions have the same area as those shown in the middle panels. The left panel for NGC 1783 shows labels for the MS, MSTO, RC, RGB, and AGB features in the CMD.
Download figure:
Standard image High-resolution imageFigure 2. Same as Figure 1, but now for NGC 1987, NGC 2108, and LW 431.
Download figure:
Standard image High-resolution image3.2.1. General Comments
Figures 1 and 2 show that the star clusters in our sample all contain a clear red clump as well as RGBs and AGBs with various extents and levels of population. Focusing on the relative F435W-band luminosities of the MSTO and the RC as well as the extent of the RGB within the individual clusters, it is clear that the clusters NGC 1987 and NGC 2108 are younger than the others in our sample. The ages of the other clusters appear to be similar to one another. Cluster ages will be quantified in Section 4. A comparison of the middle and right-hand panels in Figures 1 and 2 also shows that the MSTOs seen in the star clusters (middle panels) are brighter than those seen in the right-hand panels, which are most likely dominated by field stars. The field population is typically dominated (in terms of star number density) by a 5–6 Gyr old population with a broad MSTO located at mF435W ≃ 23.0 and mF555W ≃ 22.5 plus an associated evolved RGB population. The field population also includes stars younger than the clusters in our sample, as evidenced by the presence of MS stars that are brighter and bluer than the MSTOs of the star clusters.
A comparison of the morphologies of the MSTO regions in all star clusters in our sample with the local photometric uncertainties (see Figures 1 and 2) shows that the MSTO regions are significantly more extended than expected for a coeval simple stellar population (SSP). This is consistent with the findings of Mackey & Broby Nielsen (2007), Mackey et al. (2008), and Milone et al. (2009). However, these authors interpreted the extended MSTO regions in NGC 1751, NGC 1783, NGC 1806, and/or NGC 1846 in their photometry as due to the presence of two distinct stellar populations of identical metallicity but different age. Our photometry shows differences from those of Mackey et al. and Milone et al., which potentially affects the interpretation of how these clusters formed. These differences are discussed further in Section 7.
3.2.2. Differential Reddening
The CMDs of most star clusters in our sample reveal compact RCs and/or well-defined RGBs and AGBs that have widths which are comparable to the photometric uncertainties. Since the reddening vector is approximately perpendicular to the RGB and AGB, this suggests that spatial variations in reddening are negligible for most clusters in our sample. There are, however, two exceptions: NGC 1751 and NGC 2108, both of which have a "fuzzy" RC and RGB. To correct their CMDs for differential reddening, we follow a method similar to that used by Sarajedini et al. (2007). We divide the cluster field into several subareas (the number of subareas depends on the total number of stars found in the cluster). After defining a grid of magnitude and color intervals along the MS below the MSTO region, a fiducial ridge line for the MS is derived for all stars located within the King core radius from running medians of star magnitudes and colors. We then measure the weighted mean mF435W, mF555W, and mF814W magnitudes of stars within those grids for all subareas within the cluster. These weighted mean magnitudes define the local reddening in each subarea relative to the mean reddening within the King core radius of the cluster. These reddening values are then used to correct the magnitudes of stars in all subareas to a uniform reddening value. The effect of the correction for differential reddening is shown in Figures 3 and 4. The improvement is particularly significant for NGC 1751 where the RC becomes more compact than before the correction. The total amplitude of differential reddening within the cluster was found to be Δ E(mF435W − mF814W) = 0.14 and 0.10 for NGC 1751 and NGC 2108, respectively.
Figure 3. Portion of the mF435W vs. mF435W − mF814W CMD of NGC 1751. (a) Observed CMD. (b) After correction for differential reddening.
Download figure:
Standard image High-resolution imageFigure 4. Same as Figure 3, but now for NGC 2108.
Download figure:
Standard image High-resolution image3.3. Radial Surface Number Density Distributions
We analyze the projected surface number density of stars in the sample star clusters for two main reasons: (1) to determine regions in the CMD that are strongly dominated by stars belonging to the cluster rather than to the underlying field in the LMC and (2) to allow an evaluation of dynamical properties of the clusters, which can help shed light on the origin of the eMSTOs. The cluster centers were determined by fitting a two-dimensional Gaussian to an image constructed from the completeness-corrected number density of stars brighter than the magnitude for which the completeness is 50% in the central regions in a given star cluster. This image was constructed using a bin size of 50 × 50 pixels (i.e., 2 5 × 2
5 × 2 5). Note that using the number density instead of surface brightness avoids biases that can arise because of a few bright stars near the center. The typical uncertainty of the centering procedure was ±5 pixels in either axis. The ellipticities of the clusters were derived by running the task ellipse within iraf/stsdas6 on the number density images mentioned above. Derived ellipticities stayed constant with radius to within the uncertainties. The area sampled by the ACS image was then divided into a number of centered, concentric elliptical annuli. The number of such annuli was chosen in an adaptive manner so as to include a minimum of 100 stars per annulus. The surface number density was corrected for incompleteness by dividing the number of stars by the average completeness fraction in each annulus. For annuli with radii larger than ∼850 pixels ( 42
5). Note that using the number density instead of surface brightness avoids biases that can arise because of a few bright stars near the center. The typical uncertainty of the centering procedure was ±5 pixels in either axis. The ellipticities of the clusters were derived by running the task ellipse within iraf/stsdas6 on the number density images mentioned above. Derived ellipticities stayed constant with radius to within the uncertainties. The area sampled by the ACS image was then divided into a number of centered, concentric elliptical annuli. The number of such annuli was chosen in an adaptive manner so as to include a minimum of 100 stars per annulus. The surface number density was corrected for incompleteness by dividing the number of stars by the average completeness fraction in each annulus. For annuli with radii larger than ∼850 pixels ( 42 5), care was taken to account for the limited azimuthal coverage of the cluster by the ACS/WFC image. Specifically, we first constructed a parallelogram whose edges stay 50 pixels within the area exposed by all (three) F555W exposures of a given star cluster. We then constructed "elliptical pie slices" that subtend angle intervals which are radius dependent in a way such that the angle subtended by the outer end of the pie slice fits fully within the parallelogram mentioned above. Stars were then counted within those pie slices, and the areas of each pie slice were evaluated to measure surface number densities. Error values were derived from Poisson statistics of the star number counts. Radii are expressed in terms of the "equivalent" radius of the ellipse, where a is the semimajor axis of the ellipse and
5), care was taken to account for the limited azimuthal coverage of the cluster by the ACS/WFC image. Specifically, we first constructed a parallelogram whose edges stay 50 pixels within the area exposed by all (three) F555W exposures of a given star cluster. We then constructed "elliptical pie slices" that subtend angle intervals which are radius dependent in a way such that the angle subtended by the outer end of the pie slice fits fully within the parallelogram mentioned above. Stars were then counted within those pie slices, and the areas of each pie slice were evaluated to measure surface number densities. Error values were derived from Poisson statistics of the star number counts. Radii are expressed in terms of the "equivalent" radius of the ellipse, where a is the semimajor axis of the ellipse and  its ellipticity. The resulting radial surface number density profiles were fitted with a King (1962) model combined with a constant background level:
its ellipticity. The resulting radial surface number density profiles were fitted with a King (1962) model combined with a constant background level:
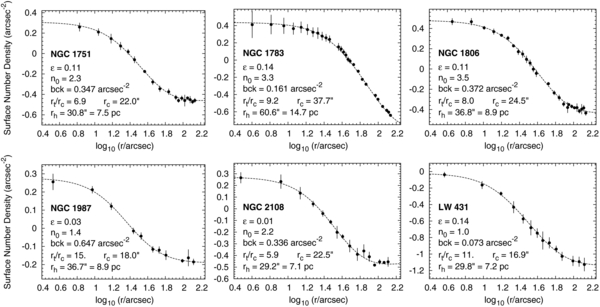
where n0 is the central surface number density, rc is the core radius, and c ≡ (rt/rc) is the concentration index (rt being the tidal radius). The best-fit King models were selected using a χ2 minimization routine that involves varying values of c. Figure 5 shows the best-fit models along with the individual surface number density values for each star cluster in our sample (except NGC 1846 for which we refer the reader to Paper I). Radius values in arcsec were converted to parsecs using the distance moduli listed in Table 3.
Figure 5. Radial surface number density profiles of the star clusters in our sample. The points represent observed values. The dashed lines represent the best-fit King models (cf. Equation (1)) whose parameters are shown in the legends. The names and ellipticities of the clusters are also shown in the legends.
Download figure:
Standard image High-resolution image3.3.1. Selection of Cluster-Dominated Regions on the CMD
We establish portions of the CMD that are strongly dominated by cluster stars using the statistical method described in detail in Paper I. Briefly, we compared star surface number densities in selection boxes on the CMD from two radial ranges: "inner" stars with log (r) ⩽ 1.5 versus "outer" stars with 2.0 ⩽ log (r) ⩽ 2.2 (with radius r in arcsec). Selection boxes for which the "inner/outer" surface number density ratio (after completeness correction) exceeded the value given by the best-fit King model to all stars in the ACS image were tagged as dominated by cluster stars.
Stars in regions on the CMD found to have less than 20% contamination by field stars are shown with black dots in all CMDs shown in this paper, whereas the other stars are shown with gray dots.
4. ISOCHRONE FITTING
We fit isochrones to the CMDs of the star clusters in our sample to determine their age, metallicity, and [α/Fe] ratios. We use three sets of stellar models with predictions computed for the ACS/WFC filter system: Padova isochrones (Marigo et al. 2008; Girardi et al. 2008), Teramo isochrones (sometimes referred to as BaSTI isochrones; Pietrinferni et al. 2004, 2006), and Dartmouth isochrones (Dotter et al. 2008).
Padova isochrones. We use the default models which involve scaled solar abundance ratios (i.e., [α/Fe] = 0.0) and which include some degree of convective overshooting (see Girardi et al. 2000). The Padova isochrones are calculated through the thermally pulsing AGB (TP–AGB) stage of stellar evolution. Using the web interface of the Padova team,7 we construct a grid of isochrones that covers the ages 0.3 ⩽ τ [Gyr] ⩽ 3.0 (where τ is the age) with a step of Δτ = 0.05 Gyr and metallicities Z = 0.001, 0.002, 0.004, 0.006, 0.008, 0.01, 0.02, and 0.03.
Teramo isochrones. We use that team's Web site8 to construct grids of isochrones that cover the same ages and metallicities as for the Padova models mentioned above, except that Z = 0.006 is not available. We use the Teramo isochrones with [α/Fe] = 0.0 which are calculated through the TP–AGB phase and which include prescriptions for convective overshooting.
Dartmouth isochrones. We use the full grid available from their Web site9 which covers the ages 0.25 ⩽ τ [Gyr] ⩽ 1.0 with Δτ = 0.05 Gyr and 1.0 < τ [Gyr] ⩽ 5.0 with Δτ = 0.25 Gyr, metallicities [Fe/H] = −2.5, −2.0, −1.5, −1.0, −0.5, 0.0, +0.3, and +0.5, and [α/Fe] = −0.2, 0.0, +0.2, +0.4, +0.6, and +0.8. Isochrones with a finer grid in age and/or [Fe/H] were also created around the initial best-fit values found for the star clusters in our sample (see the next section), using the interpolation routine made available through the Dartmouth team Web site. The Dartmouth isochrones terminate at the He flash, so that the HB and AGB sequences are not included. Finally, we use Dartmouth isochrones featuring enhanced helium abundance (Y = 0.33) to assess the impact of enhanced He on the MSTO region. This topic is addressed in Section 5.
4.1. Fitting Method
The isochrone fitting was performed using the method described in detail in Paper I. We provide a less comprehensive description here, and concentrate most on parts of the procedure that are additions to the steps described in Paper I. We start the isochrone fitting by using parameters that involve pairs of fiducial points on the CMD that are (1) relatively easy to measure or determine from both the data and the isochrone tables, (2) sensitive to at least one population parameter such as age or metallicity, and (3) independent of the distance and foreground reddening of the cluster.
In the case of clusters with a well-defined RGB bump (i.e., NGC 1751, NGC 1783, NGC 1806, and NGC 1846), we use the following parameters (cf. Paper I).
- 1.The difference in magnitude between the MSTO and the RGB bump,10 called ΔBMSTORGBB and ΔVMSTORGBB in the B and V filters, respectively. The MSTO is defined as the point where a polynomial fit to the stars (or the isochrones) near the turnoff is vertical in the CMD. We define the location of the RGB bump in the isochrones as the average magnitude and color of isochrone RGB entries between the two masses at which the magnitudes and colors "turn around" in direction on the CMD with increasing stellar mass.
- 2.The difference in color between the MSTO and the RGB bump, referred to as Δ(B − I)MSTORGBB and Δ(V − I)MSTORGBB.
- 3.The slope of the RGB. This was evaluated using the (mean) color of the RGB stars at two fiducial magnitudes, namely at mRGBB + 1 and mRGBB − 0.75. The former magnitude was chosen to represent a point intermediate between the RGB bump and the lower end of the RGB; the latter magnitude was chosen to avoid issues related to confusing RGB with AGB stars on the CMD. The mean colors of the RGB stars were derived from the CMD by means of a polynomial fit to the RGB star positions in the CMD. The predicted colors were derived from a linear interpolation between isochrone table entries.
The main reason for using the RGB bump as a prime parameter in this context is that all three isochrone families can be used this way. However, in the case of clusters for which the location of the RGB bump is not well constrained from the observations (i.e., NGC 1987, NGC 2108, and LW 431), we replace parameters (1) and (2) above with the following ones.
- 1a.The difference in magnitude between the MSTO and the red clump (RC), named ΔBMSTORC and ΔVMSTORC in the B and V filters, respectively. We simply calculate the mean observed magnitude and color of stars in a box centered on the RC by eye. For the isochrones, we define the "mean" location of the RC as follows. After identifying the start of the RC in the Padova and Teramo isochrone tables, isochrone magnitudes and colors are recorded up to the point where the difference in color between two subsequent isochrone entries becomes ⩾3σ larger (redder) than the average color accumulated from the isochrone entries in the RC recorded up to that point. This procedure was empirically verified to yield the appropriate end point of the RC. Weighted magnitudes and colors for the RC are then derived from the recorded isochrone entries. To simulate the distribution of stars in the RC of a star cluster, weight factors are assigned during the latter operation by using a Salpeter (1955) mass function.
- 2a.The difference in color between the MSTO and the RC, named Δ(B − I)MSTORC and Δ(V − I)MSTORC.
The sensitivity of parameters (1), (2), and (3) mentioned above to population parameters in the age range 1–3 Gyr was illustrated in Figures 9–11 of Paper I for all three isochrone families used here. Since we are using parameters (1a) and (2a) instead of (1) and (2) for some clusters in this paper, we now show a comparison of the sensitivity of parameters (1), (1a), (2), (2a), and (3) to age and [Fe/H] for the Padova and Teramo isochrone families in Figures 6 and 7 for the age range 1–3 Gyr. These plots show that while details of the dependences of ΔBMSTORC and Δ(B − I)MSTORC on age and [Fe/H] are different from those of ΔBMSTORGBB and Δ(B − I)MSTORGBB, both sets of parameters do yield mutually consistent results when compared with the observed values. As already mentioned in Paper I, the RGB slope is highly sensitive to metallicity and almost independent of age in the range studied here.
Figure 6. Dependence of five distance and reddening-independent parameters involving fiducial points on the mF435W vs. mF435W − mF814W CMD on age and metallicity. Predictions from the Padova isochrones (Marigo et al. 2008) are shown. Top panels: slope of the RGB as defined in Section 4.1. Second row of panels: BRC − BMSTO. Third row of panels: BRGBB − BMSTO. Fourth row of panels: (B − I)RC − (B − I)MSTO. Bottom panels: (B − I)RGBB − (B − I)MSTO. Error bars in the left and right panels reflect the variation of the parameter values among the isochrones with different metallicities and ages, respectively. The dashed lines in each panel represent the measurements of these parameters for NGC 1806.
Download figure:
Standard image High-resolution imageFigure 7. Same as Figure 6, but now for the Teramo isochrones (Pietrinferni et al. 2004). The filled circles refer to the isochrones with convective overshooting, while the open circles refer to those without.
Download figure:
Standard image High-resolution imageWe then select all isochrones (within each family) for which the values of the three parameters mentioned above lie within 2σ of the measurement uncertainty of those parameters on the CMDs. This yielded 6–15 isochrones depending on the isochrone family. For these isochrones, we then find the best-fit values for distance modulus (m − M)0 and foreground reddening AV by means of a least-squares fitting program. For the filter-dependent reddening we use AF435W = 1.351 AV, AF555W = 1.026 AV, and AF814W = 0.586 AV (cf. Paper I).
Finally, the isochrones were overplotted onto the CMDs for visual examination. As mentioned in Paper I for NGC 1846, this revealed that there was a small but systematic offset in [Fe/H] between best-fit isochrones for mF435W versus mF435W − mF814W and mF555W versus mF555W − mF814W in the sense that the derived value of [Fe/H] was always higher for the isochrone fit to mF555W versus mF555W − mF814W than to mF435W versus mF435W − mF814W. This effect was most significant for the Padova and Teramo isochrones, and we have suggested (see Paper I) that the cause is related to the fact that those two isochrone families derive their Teff–color relations from the ATLAS9 stellar atmosphere models of R. L. Kurucz (e.g., Castelli & Kurucz 2003) which have been shown to contain more flux in the range ∼5000–6500 Å (including much of the V band) than empirical star spectra from the Pickles (1998) library at the same stellar type (Maraston et al. 2008). Model SEDs therefore have bluer V − I colors than observed for RGB stars, consistent with what we see. Conversely, the Dartmouth isochrones are based on the Phoenix model atmospheres (e.g., Hauschildt et al. 1999) which include hundreds of millions more molecular transitions than the ATLAS9 models and hence a more accurate opacity modeling. Because of this effect, we focus on the mF435W versus mF435W − mF814W CMDs for deriving population parameters.
The best-fit isochrones and their population parameters are listed for each isochrone family in Table 2 and shown in Figures 8 and 9, superposed onto the CMDs. The best-fit isochrones of each model family generally match the various stellar sequences well.11 However, one significant difference among the isochrones is seen on the upper RGB for clusters NGC 1783 and NGC 1806 (the same was seen for NGC 1846; see Paper I). The best-fit Dartmouth isochrones typically provide a better fit to the upper RGB than the Padova and Teramo isochrones, both of which appear bluer than the observed stars. This difference is briefly discussed in Section 4.2 below.
Figure 8. Best-fit isochrones (solid lines) are superposed onto the CMDs of NGC 1751, NGC 1783, and NGC 1806 (the CMDs are the same as those shown in Figure 1). The left-hand panels show Padova isochrones, the middle panels show Teramo isochrones, and the right-hand panels show Dartmouth isochrones. Black dots indicate stars in areas of the CMD contaminated by field stars by less than 20%, while gray dots indicate stars in other areas.
Download figure:
Standard image High-resolution imageFigure 9. Same as Figure 8, but now for NGC 1987, NGC 2108, and LW 431.
Download figure:
Standard image High-resolution imageFigure 10. Illustration of the effect of the [α/Fe] ratio on the isochrone morphology along the RGB as well as on the derived age and [Fe/H] for NGC 1783. Panels (a) through (c) show the best-fit Dartmouth isochrones for [α/Fe] = 0.0, +0.2, and +0.4, respectively, in mF435W vs. mF435W − mF814W. Panels (d) through (f) do the same in mF555W vs. mF555W − mF814W. The legends list the best-fit population properties in each case. Note the effect of the [α/Fe] ratio on the slope and curvature of the RGB, as well on the resulting age and [Fe/H].
Download figure:
Standard image High-resolution imageFigure 11. Same as Figure 10, but now for NGC 1806.
Download figure:
Standard image High-resolution imageTable 2. Best-fit Population Parameters of the Star Clusters Studied in this Paper as Derived from Different Isochrone Families
| Cluster | Padova Fitsa | Teramo Fitsa | Dartmouth Fitsb | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Age | (m − M)0 | AV | Age | (m − M)0 | AV | Age | (m − M)0 | AV | |
| NGC 1751 | 1.40 ± 0.05 | 18.50 ± 0.02 | 0.38 ± 0.02 | 1.30 ± 0.05 | 18.55 ± 0.02 | 0.40 ± 0.02 | 1.50 ± 0.02 | 18.48 ± 0.02 | 0.40 ± 0.02 |
| NGC 1783 | 1.70 ± 0.05 | 18.49 ± 0.03 | 0.00 ± 0.02 | 1.60 ± 0.05 | 18.50 ± 0.02 | 0.02 ± 0.02 | 1.80 ± 0.02 | 18.40 ± 0.02 | 0.04 ± 0.02 |
| NGC 1806 | 1.60 ± 0.05 | 18.50 ± 0.03 | 0.05 ± 0.03 | 1.60 ± 0.05 | 18.45 ± 0.02 | 0.05 ± 0.02 | 1.80 ± 0.02 | 18.40 ± 0.02 | 0.07 ± 0.02 |
| NGC 1846 | 1.70 ± 0.05 | 18.42 ± 0.03 | 0.07 ± 0.02 | 1.60 ± 0.05 | 18.50 ± 0.02 | 0.08 ± 0.01 | 1.90 ± 0.03 | 18.41 ± 0.02 | 0.09 ± 0.02 |
| NGC 1987 | 1.10 ± 0.05 | 18.37 ± 0.03 | 0.12 ± 0.02 | 1.10 ± 0.05 | 18.38 ± 0.02 | 0.11 ± 0.02 | 1.00 ± 0.05 | 18.38 ± 0.02 | 0.23 ± 0.03 |
| NGC 2108 | 1.00 ± 0.05 | 18.45 ± 0.02 | 0.48 ± 0.02 | 1.00 ± 0.05 | 18.48 ± 0.02 | 0.48 ± 0.01 | 1.00 ± 0.05 | 18.40 ± 0.02 | 0.55 ± 0.02 |
| LW 431 | 1.70 ± 0.05 | 18.45 ± 0.03 | 0.14 ± 0.02 | 1.60 ± 0.05 | 18.46 ± 0.02 | 0.15 ± 0.02 | 1.90 ± 0.05 | 18.38 ± 0.02 | 0.16 ± 0.02 |
Notes. Column 1: name of star cluster. Column 2: adopted age in Gyr. Column 3: age range in Gyr associated with the width of the observed MSTO region. Column 4: adopted [Fe/H] in dex. Column 5: adopted distance modulus in mag. Column 6: adopted foreground V-band reddening in mag. aFor the Padova and Teramo isochrones, the best-fit [Fe/H] was −0.40 ± 0.05 for all clusters. bFor the Dartmouth isochrones, the best-fit [Fe/H] and [α/Fe] were −0.50 ± 0.05 and +0.2 ± 0.1, respectively, for all clusters.
Download table as: ASCIITypeset image
In order to find the spread in age that can explain the extended morphology of the MSTO regions of the clusters in our sample, we first note that the width of the RGB in all clusters is consistent with photometric errors and that the slope of the RGB in each cluster does not show evidence for an intrinsic spread in [Fe/H]. Hence we fix [Fe/H], AV, and (m − M)0 and vary the isochrone age using steps of 0.05 Gyr until one reaches the extremes of the eMSTO region populated by the cluster stars. These age spreads are listed in Table 3, along with the final adopted parameters for the clusters in our sample, including their uncertainties that reflect both errors associated with the isochrone fitting and systematic uncertainties related to the use of the different stellar models. The determination of the population parameters adopted and their uncertainties are discussed further in Section 4.3 below.
Table 3. Adopted Population Parameters of the Star Clusters Studied in This Paper
| Cluster | Age | Age Range | [Fe/H]a | (m − M)0 | AV | log |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
| NGC 1751 | 1.40 ± 0.10 | 1.15 – 1.65 | −0.50 ± 0.10 | 18.50 ± 0.03 | 0.40 ± 0.01 | 4.82 ± 0.09 |
| NGC 1783 | 1.70 ± 0.10 | 1.50 – 1.90 | −0.50 ± 0.10 | 18.46 ± 0.04 | 0.02 ± 0.02 | 5.25 ± 0.09 |
| NGC 1806 | 1.67 ± 0.10 | 1.57 – 1.92 | −0.50 ± 0.10 | 18.46 ± 0.04 | 0.05 ± 0.01 | 5.03 ± 0.09 |
| NGC 1846 | 1.73 ± 0.10 | 1.53 – 1.93 | −0.50 ± 0.10 | 18.45 ± 0.05 | 0.08 ± 0.01 | 5.17 ± 0.09 |
| NGC 1987 | 1.05 ± 0.05 | 0.95 – 1.20 | −0.50 ± 0.10 | 18.38 ± 0.02 | 0.16 ± 0.04 | 4.49 ± 0.09 |
| NGC 2108 | 1.00 ± 0.05 | 0.90 – 1.10 | −0.50 ± 0.10 | 18.45 ± 0.03 | 0.50 ± 0.03 | 4.41 ± 0.09 |
| LW 431 | 1.73 ± 0.10 | 1.53 – 1.93 | −0.50 ± 0.10 | 18.43 ± 0.03 | 0.15 ± 0.01 | 4.00 ± 0.09 |
Notes. Column 1: name of star cluster. Column 2: adopted age in Gyr. Column 3: age range in Gyr associated with the width of the observed MSTO region. Column 4: adopted [Fe/H] in dex. Column 5: adopted distance modulus in mag. Column 6: adopted foreground V-band reddening in mag. Column 7: logarithm of photometric mass (in M☉). a[α/Fe] = +0.2 ± 0.1 is adopted for all clusters.
Download table as: ASCIITypeset image
Table 3 also includes present-day cluster masses which are estimated from the total V magnitudes listed in Table 1 and the AV, (m − M)0, [Fe/H], and mean age listed in Table 3. The masses use the predicted by the SSP models of Bruzual & Charlot (2003), assuming a Salpeter (1955) initial mass function (IMF). The latter models were recently found to provide the best fit (among popular SSP models) to observed integrated-light photometry of LMC clusters with ages and metallicities measured from CMDs and spectroscopy of individual RGB stars in the 1–2 Gyr age range (Pessev et al. 2008).
4.2. Influence of [α/Fe] Abundance Ratio
We assess the influence that non-solar [α/Fe] abundances would have on the derived age and metallicity by comparing our CMD with Dartmouth isochrones for different values of [α/Fe]. The result is illustrated in Figures 10 and 11, which show the best-fit Dartmouth isochrones for [α/Fe] = 0.0, +0.2, and +0.4 superposed onto the mF435W versus mF435W − mF814W and mF555W vresus mF555W − mF814W CMDs of NGC 1783 and NGC 1806, the two star clusters in our sample (in addition to NGC 1846, cf. Paper I) that have RGB sequences sampled well enough to allow this exercise. Note that all three isochrones fit the MSTO and RGB bump locations well, which is likely (at least partly) due to the fitting method we used (see above in Section 4). However, the detailed fits along the RGB differ significantly from one [α/Fe] value to another. This is best seen in the mF435W versus mF435W − mF814W CMD. In particular, there is a relation between the value of [α/Fe] and the curvature of the RGB in the sense that larger [α/Fe] yields stronger curvature for the RGB.
As already mentioned in Paper I for NGC 1846, larger values of [α/Fe] result in younger fitted ages. Hence there is a degeneracy between age and [α/Fe] if one does not take the detailed morphology of the RGB into account. From the results for NGC 1783, NGC 1806, and NGC 1846, the amplitude of this effect is a decrease of 9.3% (±1.0%) in age for an increase in [α/Fe] of 0.2 dex.
As Figures 10 and 11 show, the best fit to the full RGB is achieved using the isochrone with [α/Fe] = +0.2 for all clusters for which the extent and sampling of the RGB is sufficient to permit this comparison. Since the fit of the Dartmouth isochrones with [α/Fe] = +0.2 dex to the RGBs is clearly better than any isochrone that uses solar abundance ratios in any of the three families, we adopt [α/Fe] = +0.2 for NGC 1751, NGC 1783, NGC 1806, NGC 1846, and LW 431. Future spectroscopic determinations of [α/Fe] in RGB stars of these clusters and the surrounding field population would be very useful to confirm or deny the trends found here from photometry.
4.3. Adopted Population Properties and their Systematic Uncertainties
We evaluate "mean" ages of the star clusters in our sample as follows. As to the clusters for which we adopt [α/Fe] = +0.2 (i.e., all clusters except NGC 1987 and NGC 2108, the two youngest ones), we first consider the best-fit ages found for these clusters using the Dartmouth isochrones that employ [α/Fe] = 0.0. Mean values and standard deviations of the ages found from all three sets of isochrone families that include treatment of convective overshooting are then derived (at [α/Fe] = 0.0). Finally, those mean ages are converted to the equivalent for [α/Fe] = +0.2 using the relation between age and [α/Fe] mentioned in Section 4.2 above. As to NGC 1987 and NGC 2108, which are too young to exhibit an RGB bump, the isochrone fitting method employed here (see Section 4.1) does not work with Dartmouth isochrones. Hence we average the results from the Padova and Teramo isochrone families for those clusters. We note that the "by eye" Dartmouth isochrone fits shown in Figure 9 for those clusters do have ages and [Fe/H] values consistent with the Padova and Teramo isochrone fits.
We quantify systematic uncertainties in derived age, [Fe/H], distance, and reddening by comparing our best-fit results from each set of isochrones that includes treatment of convective overshooting, as compiled in Table 2. These results yield systematic uncertainties of ±7% in age, ±0.1 dex in [Fe/H], ±0.05 mag in (m − M)0 (≃ 5% in linear distance), and ±0.02 mag in AV (≃15%). We suggest that these values represent typical systematic uncertainties associated with the determination of population parameters of intermediate-age star clusters from mF435W versus mF435W − mF814W CMD fitting by isochrones of any given stellar model.
5. CONSTRAINTS ON HELIUM ABUNDANCE SPREADS
Massive GCs in our Galaxy such as ω Cen, NGC 2808, NGC 1851, and 47 Tuc have multiple MS and/or SGB sequences, which are typically interpreted as populations with different helium abundance (e.g., Piotto et al. 2007; Milone et al. 2008; Anderson et al. 2009). Note that these Galactic GCs are much more massive than the LMC clusters in our sample and were even more so at their birth since they have undergone ∼10 Gyr more mass loss due to disruption processes. Even so, helium is a natural product of the same chemical reactions that are thought to be responsible for the Na-rich and O-poor stars in the Na–O anticorrelations among stars in Galactic GCs (e.g., Gratton et al. 2004). Since the eMSTO phenomenon in the intermediate-age clusters in our sample may well be causally associated with the Na–O anticorrelations within Galactic GCs, we evaluate the possibility that enhanced He may contribute to the eMSTO feature. We use the Dartmouth isochrones with moderate He enhancement, namely He mass fraction Y = 0.33.12
Taking into account that the width of the RGB in our sample is consistent with small uncertainties in the photometry (of order 0.01 mag in mF435W − mF814W), we first hold (m − M)0, AV, and [Fe/H] constant at the values listed in Table 2, and choose ages consistent with the bright and faint ends of the eMSTO region for each cluster as listed in Table 3. Figure 12 shows the CMDs of NGC 1806 and NGC 1846 along with isochrones for the ages and [Fe/H] described above, both for Y = 0.25 (i.e., primordial He) and Y = 0.33 (enhanced He). Note that the He-enriched isochrones do not fit the CMDs well. In particular, the Y = 0.33 isochrones have SGBs and MSs that are ∼0.3 mag too faint relative to the data (and the best-fit isochrones that use primordial He). The morphology of the MSTO region of the star clusters is also distinctly different from that of the isochrones with enhanced He. The latter indicate an MSTO region which lies roughly Δ (mF435W − mF814W) ≃ 0.15 mag on the blueward (hot) side of the MSTO of the clusters. Finally, the RGB sequences of the He-enriched isochrones are significantly bluer than the RGB of the clusters.
Figure 12. Predictions from Dartmouth isochrones with primordial (solid lines) and enhanced (dashed lines) helium abundance. The CMDs of NGC 1806 (a) and NGC 1846 (b) are shown. Solid lines show best-fit isochrones with [α/Fe] = 0.0 for the bright end (blue) and faint end (red) of the eMSTO region. The dashed lines show isochrones with the same age, [Fe/H], and [α/Fe] as the solid lines of the same color, but now with helium mass fraction Y = 0.33.
Download figure:
Standard image High-resolution imageConsidering the alternative (albeit unlikely) possibility that the majority of the stars in these clusters have enhanced helium abundance, we then leave the age, [Fe/H], [α/Fe], (m − M)0, and AV as free parameters and repeat the isochrone fitting procedure mentioned in Section 4.1 with Y = 0.33 isochrones. We used a grid of age and [Fe/H] with steps of Δ Age = 0.05 Gyr and Δ [Fe/H] = 0.02 dex in this case, respectively, centered on the values found for primordial helium. Figure 13 depicts the two best-fit Y = 0.33 isochrones to NGC 1806 and NGC 1846, along with the best-fit isochrones listed in Table 2 for comparison purposes. While these He-enhanced isochrones are a better fit to the RGB, the SGB, and the MSTO region than those shown in Figure 12, the MSs predicted by the He-enhanced isochrones are still significantly hotter than those observed for the clusters (and of the best-fit isochrones that use primordial He abundance).
Figure 13. Similar to Figure 12, but red lines now show best-fit Dartmouth isochrones with Y = 0.25 (cf. Table 3) for the overall CMDs of NGC 1806 (a) and NGC 1846 (b). The blue and magenta lines show two of the best-fitting isochrones with Y = 0.33 to those CMDs. The parameters Age (in Gyr), [Fe/H] (in dex), and AV (in mag) of the latter two isochrones are shown in the legend (in that order, and using the same color). Note that the best-fit Y = 0.33 isochrones always have MSes that are significantly bluer than the cluster MSes.
Download figure:
Standard image High-resolution imageWe therefore conclude that He enhancement of any subpopulation of stars in these clusters must be very small. Comparing the locations of the MSs of Y = 0.33 isochrones with those of the Y = 0.25 isochrones and of the clusters, we estimate that ΔY ≲ 0.02 in the eMSTO clusters. Note that such a small range in He abundance is consistent with the moderate masses of the eMSTO clusters. Consider for example that He enhancement for a second-generation population is provided by slow stellar winds of IM–AGB stars (i.e., AGB stars with ) which produce He through the hot-bottom burning process. For that case, Renzini (2008) estimates that 0.7% of the initial mass of a stellar population is returned to the ISM as "fresh" He. For a massive eMSTO cluster like NGC 1846 with a current mass of ∼1.5 × 105 M☉ (cf. Table 3), we calculate in Paper III that its mass at an age of 10 Myr was a factor 2 – 3 higher than the current mass, depending on the degree of initial mass segregation. For an initial mass of 3 × 105 M☉, IM–AGB stars would thus produce 2100 M☉ of "fresh" He (neglecting stochastic effects associated with sampling the mass function). Under the assumptions that the second generation of stars (1) formed with a star formation efficiency  SF = 0.5 and (2) that it currently represents 65% of the stars in the cluster (see Section 6.1 below), 2100 M☉ of He would be equivalent to a helium mass fraction increase of 0.5 × 2100/(0.65 × 1.5 × 105) = 0.01 relative to the first generation. This estimate is consistent with the estimate of the upper limit on He enhancement mentioned above.
SF = 0.5 and (2) that it currently represents 65% of the stars in the cluster (see Section 6.1 below), 2100 M☉ of He would be equivalent to a helium mass fraction increase of 0.5 × 2100/(0.65 × 1.5 × 105) = 0.01 relative to the first generation. This estimate is consistent with the estimate of the upper limit on He enhancement mentioned above.
6. MORPHOLOGY OF THE MSTO REGIONS
The eMSTO regions in the clusters in our sample are likely due to the existence of more than one "simple" stellar population. To date, the presence of eMSTO regions has been interpreted as (1) bimodal age distributions (Mackey et al. 2008; Milone et al. 2009), (2) age spreads of 200–500 Myr (Goudfrooij et al. 2009; Mackey et al. 2008; Milone et al. 2009; Girardi et al. 2009; Rubele et al. 2010, 2011), and (3) spreads in rotation velocity among turnoff stars (Bastian & de Mink 2009). The latter study is the only one that does not invoke a spread in age, or star formation history, as the cause.
Bastian & de Mink (2009) claimed that a distribution of rotation velocities vrot ranging up to ∼70% of the critical break-up velocity for stars of can mimic the observed morphologies of eMSTO regions in intermediate-age clusters. Basically, increasing vrot yields cooler isochrones near the MSTO, mimicking older ages. However, the study of Girardi et al. (2011) considered effects of rotation and convective core overshoot on isochrones using newly calculated evolutionary tracks for vrot = 150 km s−1 (which is close to the peak of the observed distribution of rotation rates of such stars) and found that the effects of both rotation and convective core overshoot cannot account for the observed widths of the eMSTO region for that particular value of vrot. Furthermore, the ∼1.4 Gyr old star clusters NGC 419 and NGC 1751 have been found to host extended red clumps which require a range of ∼0.2 M☉ in the mass of the H-exhausted core. Rotation is unlikely to be able to produce this effect whereas a range in age does so naturally (Girardi et al. 2009; Rubele et al. 2011).
While further studies of the effects of stellar rotation on isochrones (e.g., using a suitable range of vrot values) should be pursued before dismissing rotation as a significant cause of eMSTO regions in intermediate-age star clusters, we focus here on age spreads which currently seem to be the more likely cause of the eMSTO regions in the intermediate-age clusters studied here. We use simulations to investigate the impact that several different parameters have on the morphology of the MSTO region, e.g., formation history, binaries, etc., and then compare the results with the observations.
6.1. Monte Carlo Simulations
We first simulate cluster CMDs where stars formed in two distinct epochs with an age difference Δτ. Each simulated cluster CMD is created by populating Dartmouth isochrones with stars randomly drawn from a Salpeter IMF between 0.1 M☉ and the RGB-tip mass. A pair of ages is chosen for each synthetic CMD from an age grid that encompasses the age interval around the best-fit age implied by the range given in Column 3 of Table 3. The grid is populated using an age increment of 50 Myr, which is similar to the age of the youngest (most massive) types of stars that have been put forward as plausible donors of material from which a new stellar generation can be formed (i.e., the FRMS and massive binary stars). For each pair of ages, we vary the relative (mass) fraction in the younger population from 0.80 to 0.20 in 0.05 increments. The total number of simulated stars is normalized to the observed number of stars brighter than the 50% completeness limit. We add an unresolved binary companion to a fraction (see below) of the stars, drawn from the same mass function (i.e., using a flat primary-to-secondary mass ratio distribution). Finally, we add photometric errors to the artificial stars, modeled after the actual distribution of photometric uncertainties.
We use the width of the upper MS, i.e., the part brighter than the turnoff of the field stellar population and fainter than the MSTO region of the clusters, to determine the binary star fraction in our sample clusters. We estimate the internal systematic uncertainty in binary fraction to ±5% and defer a more detailed discussion of binary parameter degeneracies, in particular binarity versus mass fractions of stellar generations, to a future paper. For the purposes of this work the results do not change significantly within ∼10% of the binary fraction.
In order to compare the observed and simulated MSTO regions, we use a "pseudo-age" distribution. The pseudo-age distribution is determined by constructing a parallelogram in the CMD with (1) one axis approximately parallel to the isochrones, (2) the other axis approximately perpendicular to the isochrones, and (3) located in a region of the MSTO where the split between the isochrones is relatively evident. The (mF435W − mF814W, mF435W) coordinates of the stars in the CMD are then transformed into the reference coordinate frame defined by the two axes of the parallelogram, and then considering the distributions of the coordinates of the stars in the direction perpendicular to the isochrones. To translate the latter coordinate to age, the same procedure is done for the Dartmouth isochrones for an age range that covers the observed extent of the MSTO region of the cluster in question, using an age increment of 0.05 Gyr. The relationship between age and the coordinate in the direction perpendicular to the isochrones is then determined using a polynomial least-squares fit. Since binary stars influence the distribution of stars in the MSTO region to some (albeit small) extent, we call the resulting age parameter "pseudo-age."
The procedure mentioned above is illustrated in Figures 14–17. The top panels show the simulated and observed CMDs and the parallelogram mentioned above (in blue, with the reference axis along the isochrones in red). The bottom panels show the corresponding pseudo-age distributions. These were calculated using the non-parametric Epanechnikov-kernel probability density function (Silverman 1986) for all objects in the parallelograms, in order to avoid potential biases that can arise if fixed bin widths are used. In the case of the observed CMD (i.e., panels (a) and (b)), this was done both for stars within a King core radius from the cluster center and for the "background region" for which the CMD was shown in the right panels of Figure 1. The panels (d) also list the fraction of stars in the two distinct SSPs (shown in black dots on panels (c)). The intrinsic probability density function of the pseudo-age distribution of the cluster was then derived by statistical subtraction of the background region (see panels (b)). The best-fit pair of two-SSP simulations was selected by conducting two-sample Kolmogorov–Smirnov (K–S) tests of the probability density functions of the simulations against those of the cluster data and picking the simulation with the highest p value. The properties of the selected simulations, including the best-fit binary fractions and the p values for each star cluster, are listed in Table 4.
Figure 14. (a) Enlargement of the CMD of NGC 1751 shown in the middle panel of Figure 1, focusing on the MSTO region. The blue, green, and orange curves represent Dartmouth isochrones that fit the upper end, middle, and lower end of the broad MSTO region, respectively. Their ages (in Gyr) are mentioned at the lower left corner of the panel. (b) "Pseudo-age" distributions of the cluster, using stars in the parallelograms shown in panels (a) and derived using a non-parametric density estimator (see the text in Section 6 for details). The black dashed line represents all stars, the blue dashed line represents stars in the background area scaled to the area of the ACS image used for the CMD in panel (a), and the solid line represents "all stars minus background." The red arrow in panel (a) indicates the positive direction of the X-axis of panel (b). (c) and (d) Same as panels (a) and (b), respectively, but now for simulations of two SSPs including binary stars whose properties are listed in Table 4 and described in Section 6. The legend on the top left indicates the mass fractions of the younger vs. the older SSP used in the simulation. The gray dotted line in panel (d) is a copy of the solid line in panel (b) to allow a direct comparison.
Download figure:
Standard image High-resolution imageFigure 15. Same as Figure 14, but now for NGC 1783 and NGC 1806.
Download figure:
Standard image High-resolution imageFigure 16. Similar to Figure 14, but now for NGC 1987 and NGC 2108, two of the three lowest-mass clusters in our sample. The extra panels (e) and (f) are the same as panels (c) and (d), respectively, but now for simulations of a single SSP including binary stars as described in Section 6.
Download figure:
Standard image High-resolution imageFigure 17. Same as Figure 16, but now for LW 431.
Download figure:
Standard image High-resolution imageTable 4. Properties of Best-fit Two-SSP Simulations of the Star Clusters in Our Sample
| Cluster | Age1 | Age2 | fY | fbinary | pKS |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) |
| NGC 1751 | 1.40 | 1.70 | 0.65 | 0.30 | 0.20 |
| NGC 1783 | 1.80 | 2.00 | 0.65 | 0.25 | 0.00 |
| NGC 1806 | 1.75 | 2.00 | 0.70 | 0.25 | 0.14 |
| NGC 1846a | 1.75 | 2.05 | 0.65 | 0.15 | 0.11 |
| NGC 1987 | 1.00 | 1.25 | 0.70 | 0.35 | 0.48 |
| 1.05 | 1.05 | 1.00 | 0.35 | 0.02 | |
| NGC 2108 | 0.95 | 1.10 | 0.70 | 0.45 | 0.42 |
| 1.00 | 1.00 | 1.00 | 0.45 | 0.03 | |
| LW 431 | 1.80 | 2.05 | 0.50 | 0.20 | 0.90 |
| 1.90 | 1.90 | 1.00 | 0.20 | 0.15 |
Notes. Column 1: name of star cluster. Column 2: age of youngest SSP in Gyr. Column 3: age of oldest SSP in Gyr. Column 4: best-fit mass fraction of youngest SSP. Column 5: best-fit binary fraction. Column 6: p value of two-sided K–S test of the simulated data in the parallelograms shown in Figures 14 – 17 against the observed data. See Section 6 for details. aValues taken from Paper I.
Download table as: ASCIITypeset image
During the refereeing process of this manuscript, a paper by Yang et al. (2011) appeared, reporting on simulations of the impact of interactive binaries on eMSTO morphologies of intermediate-age star clusters. Their calculations, which assume that all cluster stars are members of binary systems, show that the presence of interactive binaries would cause (1) a slight extension of the MSTO region toward the blue and (2) a "fan" of low stellar density in the CMD toward brighter magnitudes and bluer colors than the MSTO. The distribution of this "fan" on the CMD shows similarities to the presence of younger stars, although most "fan" stars are fainter than the MSTO region of younger isochrones. We believe that the actual impact of such interactive binaries on the eMSTO morphologies of the star clusters in our sample is insignificant for two main reasons. First, the extension of the MSTO region mentioned in point (1) above involves color changes that are significantly smaller than the observed color ranges encompassed by the eMSTOs shown in the current paper. Second, a comparison between the middle and right-hand panels in our Figures 1 and 2 reveals that the stars in our CMDs that could be interactive binary stars in the "fan" mentioned in point (2) above are most likely LMC field stars rather than cluster stars, since they are at least as abundant in the "field" CMD as in the "cluster" CMD.
6.2. Ability to Resolve Populations of Different Ages
How well does the method described above allow us to resolve two (or more) discrete star formation events separated in time by Δτ? To address this question we use our simulations for NGC 1783, the cluster with the highest present-day mass in our sample. We consider the simulations that involved an age of the first generation of 2.00 Gyr with Δτ values of 0 (i.e., a single SSP), 50, 100, 150, and 200 Myr, and two different mass fractions, namely, fY = 0.70 and fY = 0.50 for the younger generation. These mass fractions were chosen to bracket the values found for the clusters in our sample (cf. Table 4). Results of these simulations are shown in Figure 18. For fY = 0.50, the bimodality of the pseudo-age distribution shows up clearly for Δτ ≳ 150 Myr, while Δτ ≳ 100 Myr yields a significantly broader distribution than a single SSP. For fY = 0.70, the "hump" on the right side of the pseudo-age distribution (due to the older generation) is already readily recognizable at Δτ ≳ 100 Myr. Hence our method can recognize age bimodality in CMDs if Δτ ≳ 100–150 Myr at an age of 2.0 Gyr, i.e., 0.05 ≲ (Δτ/τ) ≲ 0.08, with the exact value depending on the mass fractions of the different generations.13
Figure 18. Illustration of age resolution of our "pseudo-age" distributions. Top panel: pseudo-age distributions of simulations of two SSPs including binary stars as described in Section 6.2, using stars in the parallelograms shown in panels (a) and (c) of Figure 15 for the case of NGC 1783. The two SSPs have equal mass fractions in this panel. The age of the older population is 2.0 Gyr, and Δ Age = 0 Myr (dashed line), 50 Myr (magenta line), 100 Myr (blue line), 150 Myr (red line), and 200 Myr (black line). Bottom panel: same as top panel, but now for the case where 70% of the stars are in the younger generation. Note that age differences between successive stellar generations of 100–150 Myr or more are discernible using this method at an age of 2 Gyr.
Download figure:
Standard image High-resolution image6.3. Comparison With Observations
As Figures 14–17 show, the distribution of observed stars in the parallelogram typically peaks near the "young" end of the age range and then declines more or less uniformly toward older as well as younger ages. A comparison of panels (b) with (d) for a given star cluster shows that the distribution of the observed stars is typically more continuous than those of the best-fit two-SSP simulations. Two-sample K–S tests confirm this visual impression. The p values of the K–S tests to compare the distributions of the simulated CMDs of two SSPs with the best-fit mass fractions of the younger population against the data do not exceed 20% for the clusters (see Table 4). NGC 1987, NGC 2108, and LW 431, the three lowest-mass clusters in our sample, do not follow this rule (see Figures 16–17); these three cases are briefly discussed below. Therefore, a main conclusion of this paper is that the more massive clusters in our sample are better explained by a population with a distribution of ages rather than by two discrete SSPs. This conclusion differs from that of Mackey et al. (2008), whose analysis favored a bimodal distribution of ages for the clusters NGC 1806 and NGC 1846 and that of Milone et al. (2009), whose analysis did so for the clusters NGC 1751, NGC 1783, NGC 1806, and NGC 1846. The smooth and extended nature of the pseudo-age distributions seems to suggest that star formation did not actually occur in discrete events. This is further discussed in Section 7 below.
As to the low-mass clusters NGC 1987, NGC 2108, and LW 431, panels (c) and (d) in Figures 16 and 17 compare pseudo-age distributions for the observations and the simulated bimodal formation histories. The K–S test comparing these distributions indicates that a bimodal age distribution results in formally acceptable fits (cf. Table 4). However, these results do not preclude a continuous distribution of ages within these clusters. We also compared the pseudo-age distributions for these three clusters with those resulting from a single-age population, as shown in panels (e) and (f) of Figures 16 and 17. The observed distributions are significantly broader than a single-age population, supporting our general conclusion that more than one "simple" population is required to explain the morphology of the MSTO regions of these low-mass clusters as well.
7. IMPLICATIONS REGARDING THE NATURE OF MULTIPLE POPULATIONS IN STAR CLUSTERS
The results of the experiments described above have important implications regarding the origin of multiple populations in star clusters in general, including the situation seen in many (ancient) GCs in our Galaxy. The following discussion is relevant for star clusters with initial masses that were too low to retain gas expelled by energetic supernova (SN) explosions and/or to capture significant numbers of field stars from their host (dwarf) galaxies. In practice this restriction corresponds roughly to masses ≲ 2 × 106 M☉ (cf. Bastian & Goodman 2006; Fellhauer et al. 2006) at an age of 13 Gyr. The clusters in our sample are indeed less massive than that upper limit.
A main result of this work is that the clusters in our sample, particularly the four most massive ones, appear to have formed stars more or less continuously for 200–500 Myr and are inconsistent with a bimodal age distribution. This result rules out scenarios where two star clusters have merged together or where a star cluster has merged with a giant molecular cloud (Bekki & Mackey 2009), since these would lead to strongly bimodal age distributions.
We believe our results constitute support for the "in situ" scenario (e.g., D'Ercole et al. 2008; Renzini 2008) in which star clusters with masses high enough to retain ejecta in slow winds of stars (as opposed to SN ejecta) of the first generation gather this material in their central regions where secondary star formation can occur. Dynamical evidence to further support this scenario for the clusters in our sample is presented in Paper III. In the context of this scenario, the hitherto suggested source(s) of the ejecta are FRMS (Decressin et al. 2007), massive binary stars (de Mink et al. 2009), and IM–AGB stars (e.g., D'Antona & Ventura 2007). Note that the ejecta from FRMS and massive binary stars are produced on timescales that are significantly shorter than those from IM–AGB stars (10–30 Myr versus 50–300 Myr, respectively; see, e.g., Decressin et al. 2007; Gratton et al. 2004; Ventura & D'Antona 2008). Since our simulations in Section 6 show that two populations with ages separated by 100–150 Myr or more would result in observable bimodality in our MSTO photometry, the combination of the observed age ranges of 200–500 Myr and the absence of clear bimodality in the pseudo-age distributions seems to suggest at face value that FRMS and/or massive binary stars could well be significant contributors to the enriched material used for the secondary stellar population(s). However, IM–AGB stars also seem likely significant contributors, since the (pseudo-)age distributions of the star clusters in our sample do typically peak at the younger end of the age range (especially for the more massive clusters in our sample).
Finally, the slow winds from all suggested stellar types would lead to chemical enrichment of light elements in the second generation of stars due to products from the CNO and ON cycles. In the context of the "in situ" scenario, one would expect to see significant and correlated variations in light element abundances (e.g., N, O, Na) among the stars in the star clusters with relatively high masses in our sample, likely in a way similar to the Na–O anticorrelation found in Galactic GCs (see also Conroy 2011; Keller et al. 2011). If instead the main cause of the eMSTO regions is not an age spread, one would not expect to see any variations in light element abundances, even in the most massive eMSTO clusters. Measuring the chemical composition of RGB stars in LMC clusters with eMSTO regions is feasible (albeit challenging) with current spectrographs on 8–10 m class telescopes (e.g., Mucciarelli et al. 2008) and should provide additional relevant evidence to help decipher the most likely scenario responsible for populating the eMSTO regions.
8. SUMMARY AND CONCLUSIONS
We have used deep BVI photometry from HST/ACS images to construct CMDs of seven intermediate-age star clusters in the LMC. We have used the ePSF fitting technique developed by J. Anderson, which returns high-accuracy photometry of cluster stars extending some 5 mag below the MSTO for all our target clusters. We fit isochrones from the Padova, Teramo, and Dartmouth groups in order to determine the best-fit stellar population parameters for the clusters in our sample. All three sets give a reasonably good fit to the CMDs, although there are significant differences between the observations and predictions in the shape of the RGB. The overall best fit to the entire CMD is typically achieved using the Dartmouth isochrones, but this distinction can formally only be made for star clusters massive enough to have a well-populated RGB.
We use the results from the isochrone fitting to quantify typical systematic errors of fitted population parameters for intermediate-age star clusters in the LMC introduced by using any one family of isochrones, and the assumption of solar [α/Fe] ratio. These systematic errors are typically of order 15% for any given stellar population parameter.
The CMDs for the clusters in our sample show a number of interesting features: (1) a very narrow RGB; (2) an MSTO region that is clearly more extended than the (fainter) single-star MS; (3) an obvious sequence of unresolved binary stars, somewhat brighter than the single-star MS. We have tested the role played by binary populations on the morphology of the MSTO region in the CMD via Monte Carlo simulations of multiple stellar generations. Our multi-SSP models include a realistic treatment of photometric uncertainties and incompleteness, and employ a flat distribution of primary-to-secondary stellar mass ratios for binary stars. A quantitative comparison of the distribution of the stars in the MSTO region with those in simulations that incorporate two SSPs with age differences consistent with the results of the isochrone fitting shows, for all clusters in our sample, that (1) their MSTO region is significantly more extended than can be explained by a single SSP and (2) the MSTO regions are statistically better described by a population with a distribution of ages rather than by two discrete SSPs as suggested by several others. We cannot, however, formally rule out a bimodal age distribution for the three lowest mass clusters in our sample.
We also conclude that any He enhancement of a second generation of stars must be very small (ΔY ≲ 0.02) for the clusters in our sample, based on a comparison of the cluster CMDs with isochrones with enhanced helium mass fractions as well as dynamical arguments.
Viable sources of the material used to form secondary generations of stars in star clusters include fast-rotating massive stars, massive binary stars, and IM–AGB stars. Further studies of element abundance ratios from high-resolution spectroscopy of individual cluster stars should be very useful in further constraining the nature of the eMSTO regions in massive intermediate-age star clusters in the LMC. In particular, if these clusters indeed host a range of stellar ages, one would expect to see correlated variations in light element abundances (e.g., N, O, Na) among the stars in the more massive star clusters in our sample, likely in a way similar to the Na–O anticorrelation found in Galactic GCs of similar (initial) mass. If instead the main cause of the eMSTO regions is not an age spread, one would not expect to see any variations in light element abundances, even in the most massive eMSTO clusters.
We are grateful to Jay Anderson for his support and help in using his ePSF-related programs, and we acknowledge stimulating discussions with Aaron Dotter, Leo Girardi, and Selma de Mink. We gratefully acknowledge the useful comments and suggestions of the anonymous referee. T.H.P. acknowledges support by the FONDAP Center for Astrophysics 15010003 and BASAL Center for Astrophysics and Associated Technologies PFB-06, Conicyt, Chile. He also gratefully acknowledges past support from the National Research Council of Canada in the form of a Plaskett Research Fellowship, during which part of this research was conducted. R.C. acknowledges support from the National Science Foundation through CAREER award 0847467. This research was supported in part by the National Science Foundation under Grant No. PHY05-51164. Support for HST Program GO-10595 was provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. We acknowledge the use of the R Language for Statistical Computing, see http://www.R-project.org.
Footnotes
- *
Based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.
- 5
The red clump is sometimes called helium clump since this is where stars undergo core helium burning.
- 6
STSDAS is a product of the Space Telescope Science Institute, which is operated by AURA for NASA.
- 7
- 8
- 9
- 10
The RGB bump marks the time in stellar evolution when the outward moving hydrogen-burning shell encounters the base of the convective envelope. At this point, fresh hydrogen fuels the fusion processes in the shell, which becomes hotter and fainter for a short period, causing stars to pile up in the CMD (e.g., Fusi Pecci et al. 1990).
- 11
Dartmouth isochrone fits could not be performed as described for the clusters NGC 1987, NGC 2108, and LW 431 due to the lack of a clear RGB bump and the fact that the Dartmouth isochrones do not extend to the RC. The Dartmouth fits shown in Figure 9 are instead "by eye" fits to the MS and MSTO.
- 12
We employ both [α/Fe] = 0.0 and [α/Fe] = +0.4 isochrones in this context; Dartmouth isochrones with [α/Fe] = +0.2 are not available for the case of enhanced He.
- 13
Obviously, the age resolution depends on the quality of the data, and needs to be evaluated individually for each data set.