ABSTRACT
We present a Monte Carlo calculation of the astrophysical rate of the 15O(α, γ)19Ne reaction based on an evaluation of published experimental data. By considering the likelihood distributions of individual resonance parameters derived from measurements, estimates of upper and lower limits on the reaction rate at the 99.73% confidence level are derived in addition to the recommended, median value. These three reaction rates are used as input for three separate calculations of Type I X-ray bursts (XRBs) using spherically symmetric, hydrodynamic simulations of an accreting neutron star. In this way the influence of the 15O(α, γ)19Ne reaction rate on the peak luminosity, recurrence time, and associated nucleosynthesis in models of Type I XRBs is studied. Contrary to previous findings, no substantial effect on any of these quantities is observed in a sequence of four bursts when varying the reaction rate between its lower and upper limits. Rather, the differences in these quantities are comparable to the burst-to-burst variations with a fixed reaction rate, indicating that uncertainties in the 15O(α, γ)19Ne reaction rate do not strongly affect the predictions of this Type I XRB model.
1. INTRODUCTION
Type I X-ray bursts (XRBs) are thought to arise from thermonuclear runaways occurring in a thin layer on the surfaces of neutron stars accreting hydrogen- and helium-rich matter from companion stars in close binary systems (Woosley & Taam 1976; Joss 1977). Accreting neutron stars in binary systems stably fuse hydrogen into helium via the temperature-independent hot CNO cycles at high accretion rates. At low accretion rates they exhibit XRBs due to the explosive burning of H or He of typical duration 10–100 s during which approximately 1039–1040 erg is liberated (Cumming 2004). If the accreted material is rich in H, the rp-process occurs after the burst ignites, potentially leading to the synthesis of nuclei up to A ≈ 100 (Schatz et al. 2001) or beyond (Koike et al. 2004; Elomaa et al. 2009). The light nuclei that participate in the CNO cycles and the heavier nuclei of the rp-process are linked by the breakout reactions 15O(α, γ)19Ne and 18Ne(α, p)21Na (Wallace & Woosley 1981; Wiescher et al. 1999). The latter reaction becomes important at higher temperatures than the former; hence 15O(α, γ)19Ne has a larger effect on the hydrogen mass fraction at the time of burst ignition than does 18Ne(α, p)21Na, thereby more strongly influencing the dynamics of the burst. For this reason, the effect of this rate on XRB models has been the subject of several investigations (Fisker et al. 2006; Cooper & Narayan 2006; Fisker et al. 2007).
While the 15O(α, γ)19Ne reaction rate has not been measured directly, intense and steady experimental efforts have enabled measurements of the decay properties of the states in 19Ne relevant to the reaction rate at XRB temperatures. These states are just above the α threshold, which lies at an excitation energy of 3.53 MeV. As they lie below the proton and neutron thresholds, the states of interest decay only by α or γ ray emission. Hence the resonant rate of 15O(α, γ)19Ne can be calculated from the radiative and α widths or equivalently the lifetimes and α decay branching ratios of the relevant states.
In this paper we assess the experimental data on the decay properties of states just above the α emission threshold in 19Ne and use a Monte Carlo technique to evaluate the reaction rate. With the results of this analysis upper and lower limits on the reaction rate at the 99.73% confidence level are derived in addition to the recommended, median value. These three reaction rates are used as input for three separate calculations of Type I XRBs using spherically symmetric, hydrodynamic simulations of an accreting neutron star. In this way the influence of the 15O(α, γ)19Ne reaction rate on the peak luminosity, recurrence time, and associated nucleosynthesis of Type I XRBs is studied and compared with previous findings.
2. DECAY PROPERTIES OF 19Ne STATES AND THE RESONANT RATE OF 15O(α, γ)19Ne
The thermonuclear rate of the 15O(α, γ)19Ne reaction at temperatures below 2 GK, the relevant range for Type I XRBs, is dominated by the contributions of resonances corresponding to states in 19Ne with excitation energies between 4 and 5 MeV. These states lie above the α decay threshold but below the thresholds for neutron or proton decay. Hence they decay only by α and γ emission and the total decay width Γ is the sum of these partial decay widths, i.e., Γ = Γα + Γγ. As these resonances are narrow compared to the spacing between adjacent levels with the same spin and parity, the contributions of the different resonances add incoherently and can be measured separately. Even in the absence of a direct measurement, the strength of a resonance can be inferred from measurements of the radiative and α widths of a state. Equivalently, measurements of the mean lifetime of a state τ and its α decay branching ratio Bα ≡ Γα/Γ suffice to determine the strength of a resonance. The resonance strength ωγ of a 19Ne state with angular momentum J formed by the capture of an α particle by 15O is given by
Taking account of the fact that the mean lifetime and total decay width are related by Γ = ℏ/τ, this implies that
The results of a number of Bα measurements of states in 19Ne have been published over the last 20 years (Magnus et al. 1990; Laird et al. 2002; Davids et al. 2003a; Davids et al. 2003b; Rehm et al. 2003; Visser et al. 2004; Tan et al. 2007; Tan et al. 2009). In addition, the lifetimes of these states have been measured by two independent groups over the past five years (Tan et al. 2005; Kanungo et al. 2006; Mythili et al. 2008). Here we critically evaluate the published measurements.
2.1. Mean Lifetime Data
All published lifetime measurements for states with excitation energies up to 4.602 MeV in 19Ne are shown in Table 1. At least two measurements of the lifetimes of all the known states with excitation energies between 1536 keV and 4602 keV have been published and agree. This agreement gives us a measure of assurance that the values are reliable, though apart from the state at 4.03 MeV, the only Doppler shifted γ-ray spectra for states above the α threshold that have been published in the literature appear in Mythili et al. (2008). For the states lying above 4602 keV, no published lifetime data exist, likely because the states decay predominantly by α decay and therefore were not observed in Doppler shift attenuation measurements. We use analog state information to deduce information on the radiative widths of the 4.71 and 5.09 MeV states. Although there are known states above 5.092 MeV and below the proton threshold, they all have α decay branching ratios consistent with 1 (Rehm et al. 2003) and their high excitation energies render them unimportant contributors to the thermally averaged reaction rate at Type I XRB temperatures. Hence we make no attempt to estimate the lifetimes of these states.
Table 1. 19Ne Level Mean Lifetime Measurements and 1σ Uncertainties in fs
| Level Energy (MeV) | Tan et al. (2005) | Kanungo et al. (2006) | Mythili et al. (2008) |
|---|---|---|---|
| 1.54 | 16 ± 4 | 19.1+0.7− 0.6 ± 1.1 | |
| 4.03 | 13+9− 6 | 11+4− 3 | 6.9 ± 1.5 ± 0.7 |
| 4.14 | 18+2− 3 | 14.0+4.2− 4.0 ± 1.2 | |
| 4.20 | 43+12− 9 | 38+20− 10 ± 2 | |
| 4.38 | 5+3− 2 | 2.9 ± 1.4 ± 0.6 | |
| 4.55 | 15+11− 5 | 18.7+3.0− 2.6 ± 2.2 | |
| 4.60 | 7+5− 4 | 7.6+2.1− 2.0 ± 0.9 |
Note. Statistical and systematic errors are listed separately in the last column.
Download table as: ASCIITypeset image
2.2. Spin and Parity Assignments
In the relevant excitation energy range, the spins and parities of most of the states are well known. The exceptions are two of the negative parity states, the 4144 keV state with a tentatively assigned spin of 9/2 and the 4200 keV state tentatively assigned to be spin 7/2. Garrett et al. (1972) initially discussed the 4144 keV state as a 7/2− state and the 4200 keV state as a 9/2− state in the context of the known rotational bands in 19F and 19Ne. Based on their distorted-wave Born approximation analyses Garrett et al. (1972) suggested swapping the spin assignments of these two states, a suggestion tentatively adopted by evaluators (Tilley et al. 1995).
We compare the spins of the 19Ne states with the spins of the presumed isobaric analog states in 19F by examining the reduced transition probabilities and the branching ratios of putative analog states. The isoscalar component dominates strong E2 transitions. The 4033 keV state in 19F undergoes a strong E2 transition. Depending on the spin, either the 4144 keV state in 19Ne or the 4200 keV state undergoes an E2 transition. Both the 3999 and 4033 keV states in 19F decay to the 5/2− state at 1346 keV. We calculate the reduced transition probabilities of the 19Ne states using the lifetimes of Mythili et al. (2008) and transition energies of Tilley et al. (1995) and Tan et al. (2005). In 19F, the 3999 keV state decays to the 1346 keV state via an M1 transition while the 4033 keV state undergoes an E2 transition. These transition strengths are tabulated in the first row of Table 2. The 4144 keV and 4200 keV states in 19Ne decay to the 5/2− state at 1508 keV. If we accept the tentative spin assignments of 9/2− and 7/2−, respectively, the 4200 keV state undergoes an M1 transition and the 4144 keV state an E2 transition. The resulting reduced transition probabilities appear in the second row of Table 2. The reduced transition probabilities calculated with the alternate spin assignments are shown in the third row of Table 2, where we see improved agreement with the 19F B(E2) value.
Table 2. Reduced M1 and E2 Transition Probabilities for Two Isobaric Analog States in 19F and 19Ne
| Nucleus | Jπ | Energy Level | B(M1) | Nucleus | Jπ | Energy Level | B(E2) |
|---|---|---|---|---|---|---|---|
| (keV) | (MeV fm3) | (keV) | (MeV fm5) | ||||
| 19F | 3999 | 0.0017+0.0010− 0.0005 | 19F | 4033 | 90 ± 20 | ||
| 19Ne | 4200 | 0.0008+0.0003− 0.0003 | 19Ne | 4144 | 460+180− 100 | ||
| 19Ne | 4144 | 0.0024+0.0010− 0.0009 | 19Ne | 4200 | 150+60− 50 |
Notes. The first row shows the transition strengths for two states in 19F. The second row contains the 19Ne transition strengths with the tentatively adopted spin assignments of Tilley et al. (1995) for the 19Ne analog states and the third row gives the transition strengths with the alternate assignment of the 19Ne spins.
Download table as: ASCIITypeset image
Although the reduced transition probabilities suggest that perhaps the spins should be swapped, the measured γ decay branching ratios support the tentative spin assignments of Tilley et al. (1995) for the 4144 keV and 4200 keV states in 19Ne. The 9/2− state at 4033 keV in 19F decays exclusively to the 1346 keV state; the 4144 keV state in 19Ne decays exclusively to the 1508 keV state, suggesting that the tentative spin assignment is justified. The 4200 keV state in 19Ne and the 3999 keV state in 19F have comparable branching ratios of 80% and 70% to the 1508 keV state in 19Ne and the 1346 keV state in 19F, respectively. It is necessary that the spins of the 4144 and 4200 keV states be measured experimentally in order to precisely constrain their contributions to the reaction rate, though this is not the largest uncertainty; for now we adopt the tentative spin assignments of Tilley et al. (1995).
2.3. α Decay Branching Ratio Data
Independent measurements of the α decay branching ratio have yielded good agreement for the high lying states, but measurements of the low lying states have been controversial. All published measurements of which we are aware are shown in Tables 3 and 4. The first measurements were reported by Magnus et al. (1990) and are shown in Table 3. The lowest energy state whose α decay branching ratio was reported in this measurement was the 4.38 MeV state, for which Bα = 0.044 ± 0.032 was given. Examination of the timing spectrum for this state shown in Magnus et al. (1990) reveals no peak and leads us to conclude that, as one would expect a priori, a 1.4σ excess over background such as this does not warrant a detection claim; these data can only be used to constrain Bα from above. In contrast, all the other Bα measurements reported in Magnus et al. (1990) appear to be based on statistically significant excesses observed over well-determined backgrounds.
Table 3. 19Ne Level α Decay Branching Ratio Bα Measurements and 1σ Uncertainties
| Level Energy (MeV) | Magnus et al. (1990) | Laird et al. (2002) | Davids et al. (2003b) |
|---|---|---|---|
| 4.03 | <4.3 × 10−4 | ||
| 4.38 | 0.044 ± 0.032 | <3.9 × 10−3 | |
| 4.55 | 0.07 ± 0.03 | 0.16 ± 0.04 | |
| 4.60 | 0.25 ± 0.04 | 0.32 ± 0.03 | 0.32 ± 0.04 |
| 4.71 | 0.82 ± 0.15 | 0.85 ± 0.04 | |
| 5.09 | 0.90 ± 0.09 | 0.90 ± 0.06 |
Note. Upper limits are cited at the 90% confidence level.
Download table as: ASCIITypeset image
Table 4. 19Ne Level α Decay Branching Ratio Bα Measurements and 1σ Uncertainties
| Level Energy (MeV) | Rehm et al. (2003) | Visser et al. (2004) | Tan et al. (2009) |
|---|---|---|---|
| 4.03 | <6 × 10−4 | 2.9 ± 2.1 × 10−4 | |
| 4.14 and 4.20 | 1.2 ± 0.5 × 10−3 | ||
| 4.38 | 0.016 ± 0.005 | 1.2 ± 0.3 × 10−3 | |
| 4.55 | 0.06 ± 0.04 | 0.07 ± 0.02 | |
| 4.60 | 0.208 ± 0.026 | 0.26 ± 0.03 | |
| 4.71 | 0.69+0.11− 0.14 | 0.80 ± 0.15 | |
| 5.09 | 0.8 ± 0.1 | 0.75+0.06− 0.07 | 0.87 ± 0.03 |
Note. Upper limits are cited at the 90% confidence level.
Download table as: ASCIITypeset image
Laird et al. (2002) measured Bα for a single state and found a value consistent with that of Magnus et al. (1990).
The measurement reported in Davids et al. (2003b) was the most sensitive made to date of the α decay of the 4.03 MeV state owing to the small, well-measured background and the selectivity of the p(21Ne, t)19Ne reaction used to populate it. Contrary to the claim made in Tan et al. (2009), net α decay events above the estimated background were observed at the location of the 4.03 MeV level in the measurement of Davids et al. (2003b). However, this small excess was not deemed statistically significant and the measurement was reported as an upper limit. No excess above the background was observed at the location of the 4.38 MeV state and therefore an upper limit on Bα was also reported for this state. We note that this 90% confidence level upper limit on Bα for the 4.38 MeV state is more than a factor of 10 smaller than the central value of the statistically insignificant detection of α decay reported from this state in Magnus et al. (1990), illustrating the peril of relying on Gaussian representations of the likelihood distributions of such measurements. The Bα values for the other states reported in Davids et al. (2003b) are consistent with those of Magnus et al. (1990).
Rehm et al. (2003) report Bα measurements of three states in 19Ne but the excitation energy resolution was around 220 keV and was insufficient to resolve adjacent levels, rendering the fitting used to deduce the two Bα central values and associated uncertainties less than wholly satisfying. Nevertheless there was no background around the 4.03 MeV level, permitting a firm upper limit on Bα for this state to be established.
Problems with the electronics used in the measurement of Visser et al. (2004) rendered the normalization of the Bα values reported there questionable. In particular, the measurements were normalized to the coincidence efficiency determined based on Bα measurements of the 5351 keV level. The measurement yielded different values of Bα for this state, all of which differed substantially from the accepted value of 1, depending on the different electronics gating configurations used in the measurement. Out of concern that the normalization is not completely understood, we have avoided using these data.
Although the relevant states were populated and separated with good energy resolution in the measurement of Tan et al. (2007), the large background was not persuasively modeled for the states below 4.55 MeV from which α decay was putatively detected. Since the backgrounds were not well determined in the 4.03, 4.14/4.20, and 4.38 MeV state α decay energy spectra shown in Figure 3 of Tan et al. (2007), the excesses claimed to be observed above them are not quantitatively reliable. Inspection of the timing spectra for these putative α decay detections from states below 4.55 MeV in 19Ne, shown in Figure 6 of Tan et al. (2009), reveals no convincing evidence of an α decay peak from the 4.03, 4.14, 4.20, or 4.38 MeV states. In contrast, the Bα values for states lying at and above 4.55 MeV appear reliable as far as the background determination and signal-to-noise ratio are concerned, and they agree with the measurements of Magnus et al. (1990).
3. MONTE CARLO REACTION RATE CALCULATION
We report here the results of a million event Monte Carlo simulation of the thermally averaged rate of the 15O(α, γ)19Ne per particle pair reaction as a function of temperature. This reaction rate is the incoherent sum of the nonresonant rate, as calculated by Dufour & Descouvemont (2000), and the contributions due to the 19Ne states at 4.03, 4.14, 4.20, 4.38, 4.55, 4.60, 4.71, and 5.09 MeV. The nonresonant contribution is negligible above 0.2 GK. While the nonresonant rate is fixed at a central value due to its totally insignificant impact on the error budget, the resonant contributions are calculated by drawing randomly from the likelihood distributions of the resonance parameters. The energies and spins of the levels adopted here are shown in Table 5. The contribution due to each resonance was calculated as follows. The energy and 1σ uncertainty of each state was taken from the compilation of Tilley et al. (1995) or calculated by using a weighted average of this and the value from Tan et al. (2005), including a discrepancy error to account for potentially discrepant data as described in Cyburt et al. (2001). The likelihood distributions for the level energies are taken to be Gaussians characterized by the means and standard deviations given in Table 5.
Table 5. 19Ne Level Angular Momenta and Energies with 1σ Uncertainties Adopted in This Work
| Level Energy (keV) | Jπ | Reference(s) |
|---|---|---|
| 4034.3(9) | 3/2+ | Tilley et al. (1995); Tan et al. (2005) |
| 4143.4(8) | (9/2)− | Tilley et al. (1995); Tan et al. (2005) |
| 4199.7(16) | (7/2)− | Tilley et al. (1995); Tan et al. (2005) |
| 4377.9(7) | 7/2+ | Tilley et al. (1995); Tan et al. (2005) |
| 4547.8(10) | 3/2− | Tilley et al. (1995); Tan et al. (2005) |
| 4601.7(9) | 5/2 + | Tilley et al. (1995); Tan et al. (2005) |
| 4712(10) | 5/2− | Tilley et al. (1995) |
| 5092(6) | 5/2+ | Tilley et al. (1995) |
Download table as: ASCIITypeset image
The lifetime of the 4.03 MeV state is drawn from the likelihood distributions for this quantity reported by Tan et al. (2005), Kanungo et al. (2006), and Mythili et al. (2008), with the weight of each measurement assigned according to the inverse of its variance. The resulting likelihood distribution realized in the one million event Monte Carlo simulation is shown in Figure 1. For Bα of this state we use the likelihood distribution derived from the measurement of Davids et al. (2003b), shown in Figure 2.
Figure 1. Likelihood distribution of the mean lifetime of the 4.03 MeV state in 19Ne based on the measurements of Tan et al. (2005), Kanungo et al. (2006), and Mythili et al. (2008). The weight assigned to each measurement is proportional to the inverse of its variance.
Download figure:
Standard image High-resolution imageFigure 2. Likelihood distribution of the α decay branching ratio of the 4.03 MeV state in 19Ne based on the measurement of Davids et al. (2003b).
Download figure:
Standard image High-resolution imagePrior to the measurement of Davids et al. (2003b), the best information on Γα for the 4.03 MeV state came from measurements of α transfer to the 19F analog state (Mao et al. 1995). The uncertainties in using isospin symmetry to deduce reduced alpha widths of states near threshold from their analog states are fairly well quantified (Fortune et al. 2010), but systematic uncertainties due to the reaction mechanism remain. Fortunately, there are reliable experimental data on Bα for the 4.03 MeV state and we need not rely on the analog state. Moreover, the most likely value of Γα for the 4.03 MeV state derived from the Monte Carlo simulation is 8 μeV, perfectly consistent with the value of 8.8(14) μeV given (for q = 9) in Mao et al. (1995).
The mean lifetimes of the 4.14 and 4.20 MeV states are drawn from the measurements of Tan et al. (2005) and Mythili et al. (2008) as described above. As we are not convinced of the reliability of the single Bα measurement for these two states reported in the literature, we calculate the α widths of these states according to
where μ is the reduced mass of the 15O+α system, a the channel radius, P the Coulomb penetrability, and θ2α the reduced α width (Teichmann & Wigner 1952). Despite some efforts to determine θ2α for the 19F analog states (de Oliveira et al. 1996; Mao et al. 1996), in our judgment no reliable experimental determinations of these reduced widths are available in the literature, so we draw them from distributions of our own construction. We conjecture that these reduced widths can be adequately represented by a lognormal distribution having a mode of θ2α = 0.005 and standard deviation of its logarithm of 1.5. In a survey of θ2α values of unbound states in the α nuclei 24Mg, 28Si, 32S, 36Ar, and 40Ca, Longland et al. (2010) find a mean value of 0.01. For comparison, the θ2α value given in de Oliveira et al. (1996) (without any uncertainty) is 0.135 for both states. We chose a channel radius of a = 5.8 fm, corresponding to r0 = 1.45 fm; we investigated different channel radii of 5.6 and 6.0 fm and found that the resulting penetrabilities changed by ∼50%, which is totally insignificant compared with the uncertainty due to the reduced width. The likelihood distribution for the Bα value of the 4.20 MeV state resulting from this calculation is shown in Figure 3.
Figure 3. Likelihood distribution of the α decay branching ratio of the 4.20 MeV state in 19Ne. We compute this using R-matrix formulae assuming the reduced α width is given by a lognormal distribution peaked at 0.005 and having a standard deviation of its logarithm of 1.5.
Download figure:
Standard image High-resolution imageWe treat the 4.38 MeV state in the same way as we do the 4.03 MeV state, with the exception being that only two independent measurements of τ exist. The likelihood distribution of Bα for this state is taken from the measurement of Davids et al. (2003b) and is shown in Figure 4.
Figure 4. Likelihood distribution of the α decay branching ratio of the 4.38 MeV state in 19Ne based on the measurement of Davids et al. (2003b).
Download figure:
Standard image High-resolution imageThe mean lifetimes of the 4.55 and 4.60 MeV states are drawn from the measurements of Tan et al. (2005) and Mythili et al. (2008). The Bα values of the 4.55 and 4.60 MeV states are drawn from the measurements of Magnus et al. (1990), Laird et al. (2002), Davids et al. (2003b), and Tan et al. (2009), with the weight of each measurement proportional to the inverse of its variance as usual.
In the cases of the 4.71 and 5.09 MeV states for which lifetime data are lacking we assume that isospin symmetry is valid and equate the reduced transition probabilities of these states with their analog states in 19F. Utilizing the lifetime measurements compiled in Tilley et al. (1995), the γ decay branching ratio measurement of Pringle & Vermeer (1989), and the resonance strength measurement of Wilmes et al. (2002), we find that the radiative widths of the 4.71 MeV and 5.09 MeV states are 46+11− 8 meV and 110+110− 60 meV, respectively. The Bα values are drawn from the measurements of Magnus et al. (1990), Davids et al. (2003b), and Tan et al. (2009).
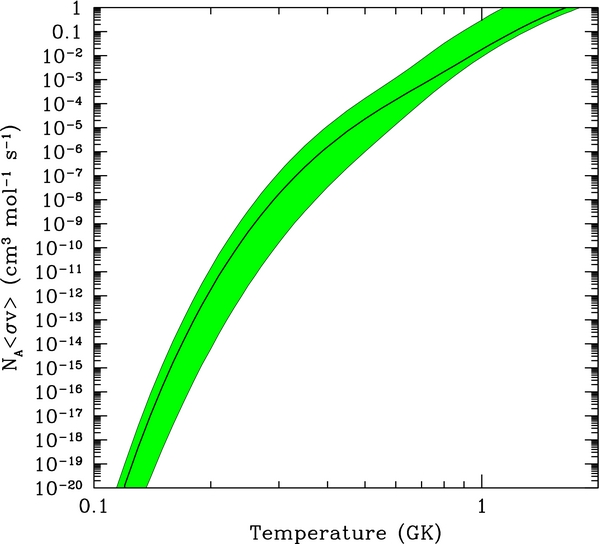
Using the resonance parameter likelihood distributions described above, we calculated the thermally averaged rate of the 15O(α, γ)19Ne per particle pair reaction as a function of temperature one million times at a range of temperatures between 0.1 and 2 GK. Analyzing the results, we determine upper and lower limits on the reaction rate at the 99.73% confidence level and adopt the median of the calculated reaction rate distribution as our recommended value. The calculated reaction rates are shown in Figure 5 and numerical values are given in Table 6.
Figure 5. Product of the Avogadro constant and the thermally averaged rate of the 15O(α, γ)19Ne per particle pair reaction as a function of temperature. Shown are the median and 99.73% confidence level upper and lower limits of the probability distribution from the Monte Carlo simulation.
Download figure:
Standard image High-resolution imageTable 6. Product of the Avogadro Constant and the Thermally Averaged Rate of the 15O(α, γ)19Ne Reaction Per Particle Pair in cm3 mol−1 s−1
| Temperature (GK) | 99.73% CL Lower Limit | Median | 99.73% CL Upper Limit |
|---|---|---|---|
| 0.1 | 1.1 × 10−25 | 1.0 × 10−24 | 7.7 × 10−24 |
| 0.2 | 6.1 × 10−15 | 1.8 × 10−12 | 1.4 × 10−11 |
| 0.25 | 2.7 × 10−12 | 4.6 × 10−10 | 3.6 × 10−9 |
| 0.3 | 1.6 × 10−10 | 1.8 × 10−8 | 1.4 × 10−7 |
| 0.35 | 3.3 × 10−9 | 2.3 × 10−7 | 1.8 × 10−6 |
| 0.4 | 3.2 × 10−8 | 1.6 × 10−6 | 1.2 × 10−5 |
| 0.45 | 2.1 × 10−7 | 7.0 × 10−6 | 5.1 × 10−5 |
| 0.5 | 1.0 × 10−6 | 2.3 × 10−5 | 0.00017 |
| 0.6 | 1.3 × 10−5 | 0.00015 | 0.0012 |
| 0.7 | 0.00011 | 0.00061 | 0.0069 |
| 0.8 | 0.00066 | 0.0021 | 0.033 |
| 0.9 | 0.0028 | 0.0066 | 0.11 |
| 1.0 | 0.0088 | 0.018 | 0.31 |
| 1.25 | 0.074 | 0.13 | 2.0 |
| 1.5 | 0.31 | 0.53 | 7.4 |
| 1.75 | 0.85 | 1.5 | 18 |
| 2.0 | 1.78 | 3.1 | 35 |
Download table as: ASCIITypeset image
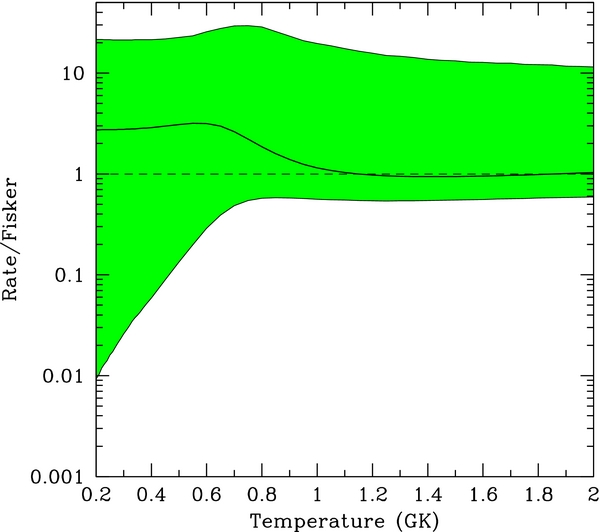
Graphical comparisons of the Monte Carlo reaction rates to the reaction rates estimated in Caughlan & Fowler (1988) and Fisker et al. (2006) are shown in Figures 6 and 7, respectively. In the temperature range from 0.1 to 2 GK the Monte Carlo lower limit on the reaction rate ranges between 2% and 91% of the lower limit of Tan et al. (2009), the Monte Carlo central value lies between 0.71 and 1.04 times that of Tan et al. (2009), and the Monte Carlo upper limit is between 3.2 and 9.4 times that of Tan et al. (2009). Hence, the central value and limits on the reaction rate estimated by Tan et al. (2009) fall well within the 99.73% CL limits on the reaction rate obtained from the Monte Carlo simulation. Comparing to the recent reaction rate estimates of Iliadis et al. (2010), we find that over the same temperature range of 0.1–2 GK our Monte Carlo lower limit on the reaction rate is between 0.03 and 3.6 times that of Iliadis et al. (2010), our central value is between 1.7 and 3.3 times that of Iliadis et al. (2010), and our upper limit is between 7 and 14 times that of Iliadis et al. (2010). However, throughout the entire temperature range characterizing the initial phase of the thermonuclear runaway (below 0.7 GK), our Monte Carlo lower limit on the reaction rate is smaller than that of Iliadis et al. (2010).
Figure 6. Ratio of the Monte Carlo reaction rate to the reaction rate estimated in Caughlan & Fowler (1988). The solid line is the ratio of the recommended reaction rate to that of Caughlan & Fowler (1988) and the shaded region is allowed at the 99.73% confidence level.
Download figure:
Standard image High-resolution imageFigure 7. Ratio of the Monte Carlo reaction rate to the reaction rate estimated in Fisker et al. (2006). The solid line is the ratio of the recommended reaction rate to that of Fisker et al. (2006) and the shaded region is allowed at the 99.73% confidence level.
Download figure:
Standard image High-resolution imageGiven the large uncertainties in the Bα values of the low lying states, it is impossible to precisely specify the fraction of the total reaction rate accounted for by the resonant contribution of any particular state. But in the Monte Carlo approach taken here it is possible to find the likelihood of a given state accounting for any definite fraction of the total reaction rate. Figure 8 shows the likelihood distributions of the fraction of the total reaction rate at 0.5 GK accounted for by the resonant contributions of the 4.03 and 4.14 MeV states. It is possible to say that at this temperature and indeed below 0.6 GK, the 4.03 MeV state likely dominates the reaction rate.
Figure 8. Likelihood distributions of the fraction of the total reaction rate at 0.5 GK accounted for by the 4.03 and 4.14 MeV states. Below 0.6 GK, the reaction rate is likely dominated by the contribution of the 4.03 MeV state with small contributions from the 4.14 and 4.20 MeV states.
Download figure:
Standard image High-resolution image4. SIMULATIONS OF TYPE I X-RAY BURSTS
In order to assess the impact of the current uncertainties in the 15O(α, γ) rate on Type I XRB models, we have performed a new set of simulations with SHIVA, a one-dimensional (spherically symmetric), hydrodynamic, implicit, Lagrangian code used extensively in the modeling of stellar explosions such as classical novae (José & Hernanz 1998) and XRBs (José et al. 2010). To this end, three different models of thermonuclear bursts, with identical input physics except for the specific choice of the 15O(α, γ)19Ne rate have been computed: the lower limit reaction rate dubbed Model A, the recommended rate Model B, and the upper limit Model C. In all cases the accretion of solar-like matter with hydrogen mass fraction X = 0.7048, helium mass fraction Y = 0.2752, and metallicity Z = 0.02 onto a 1.4 M☉ neutron star (with initial luminosity Li = 1.6 × 1034 erg s−1 = 4.14 L☉), at a mass accretion rate M☉ yr−1 (corresponding to 0.08 ), has been adopted. The Eddington accretion rate is the accretion rate that produces a luminosity at which the force due to radiation pressure equals the local gravitational force. All metals are initially assumed to be in the form of 14N, which is justified considering the rapidity with which the CNO nuclei are converted to 14N at the high temperatures reached early in the burst and the negligible energy this releases compared with accretion (Woosley et al. 2004). The model adopted in this work is qualitatively similar to model zM computed by Woosley et al. (2004) in the framework of the one-dimensional, hydrodynamic, implicit code KEPLER, as well as to the model computed by Fisker et al. (2006). We note however that whereas Woosley et al. (2004) assume a value of 10 km for the (Newtonian) neutron star radius, our model yields a value of 13.1 km following the integration of the neutron star structure. In turn, the calculations reported by Fisker et al. (2006), in a general relativistic framework, relied on a radius of 11 km for the same neutron star mass. Differences in the neutron star size and thereby surface gravity may affect the strength of the explosion through the accreted mass, peak temperature, nucleosynthesis, etc. to some extent.
The code has been linked to a fully updated nuclear reaction network containing 324 nuclides from 1H to 107Te and 1392 nuclear processes, and includes the most important charged particle induced reactions occurring among the nuclides between 1H and 107Te as well as their corresponding inverse processes (see Parikh et al. 2008 and José et al. 2010 for details). Neutron captures are not taken into account since they play a very minor role in XRB nucleosynthesis. SHIVA uses a time-dependent formalism for convective transport whenever the characteristic convective timescale becomes larger than the integration time step. Partial mixing between adjacent convective shells is treated by means of a diffusion equation (Prialnik et al. 1979). Accretion is computed by redistributing material through a constant number of envelope shells (Kutter & Sparks 1980): a thin envelope, containing 1.1 × 1018 g of material (less than 1/1000 of the total envelope mass accreted during the first bursting episode), equally distributed through all the envelope shells, is chosen as an initial condition. The model is then relaxed using a few very large time steps to guarantee hydrostatic equilibrium. More details on the adopted input physics can be found in José et al. (2010).
5. RESULTS AND DISCUSSION
A sequence of four consecutive bursts has been computed for all three models reported in this work. Summaries of the gross properties of the different sequences are given in Figure 9 and Tables 7–9. For each model, the mean mass fractions of all nuclides i that are stable or have a half-life >1 hr and are present with a mass fraction Xi > 10−9 in the envelope at the end of the fourth burst are given in Table 10.
Figure 9. Peak luminosities attained in the first four X-ray bursts and the time they were reached in the model calculations using three different 15O(α, γ)19Ne reaction rates.
Download figure:
Standard image High-resolution imageTable 7. Summary of Burst Properties for Model A
| Burst Number | Tpeak (GK) | τrec (hr) | Lpeak (L☉) | α |
|---|---|---|---|---|
| 1 | 1.10 | 5.95 | 1.4 × 105 | 50 |
| 2 | 1.25 | 4.63 | 2.9 × 105 | 29 |
| 3 | 1.21 | 5.51 | 2.3 × 105 | 38 |
| 4 | 1.21 | 5.21 | 2.7 × 105 | 30 |
Download table as: ASCIITypeset image
Table 8. Summary of Burst Properties for Model B
| Burst Number | Tpeak (GK) | τrec (hr) | Lpeak (L☉) | α |
|---|---|---|---|---|
| 1 | 1.06 | 5.88 | 9.7 × 104 | 50 |
| 2 | 1.25 | 4.44 | 2.1 × 105 | 28 |
| 3 | 1.14 | 5.19 | 1.4 × 105 | 34 |
| 4 | 1.12 | 4.84 | 1.1 × 105 | 32 |
Download table as: ASCIITypeset image
Table 9. Summary of Burst Properties for Model C
| Burst Number | Tpeak (GK) | τrec (hr) | Lpeak (L☉) | α |
|---|---|---|---|---|
| 1 | 1.03 | 5.77 | 7.7 × 104 | 52 |
| 2 | 1.26 | 4.57 | 1.9 × 105 | 27 |
| 3 | 1.17 | 5.00 | 1.2 × 105 | 33 |
| 4 | 1.17 | 4.72 | 1.5 × 105 | 29 |
Download table as: ASCIITypeset image
As a framework for our discussion, we present first a summary of the results for Model B, in which the recommended 15O(α, γ)19Ne rate has been adopted. As shown in Table 8, peak temperatures Tpeak ∼ 1.1–1.3 GK and peak luminosities Lpeak ∼ (1–2) × 105 L☉ are reached in this model. Recurrence times between bursts around τrec ∼ 4.5–6 hr and α ∼ 28–50, have also been obtained. The ratio between persistent and burst luminosities, α, is defined as
with the latter integrated over the time during which the burst exceeds 1% of its peak luminosity, τ0.01. During the interburst period, the accretion luminosity, erg s−1, will hide the thermal emission from the cooling ashes.
The values reported for Model B are qualitatively in agreement with those inferred from several XRB sources, such as the textbook burster GS 1826-24 [τrec = 5.74 ± 0.13 hr, α = 41.7 ± 1.6], 4U 1323-62 [τrec = 5.3 hr, α = 38 ± 4], or 4U 1608-52 [τrec = 4.14–7.5 hr, α = 41–54], to quote a few examples from Galloway et al. (2008). From the nucleosynthesis viewpoint, the main nuclear flow is dominated by the rp-process (rapid proton-captures and β+ decays), the 3α-reaction, and the αp-process (a sequence of (α, p) and (p, γ) reactions). The main flow proceeds away from the valley of stability, eventually reaching the proton drip line beyond A = 38. In this context, much of the initial H and 4He is transformed into heavier nuclei. However, it is important to stress the presence of some unburned H (X = 0.05) and 4He (Y = 0.11) in the envelope at the end of the fourth burst (see Table 10). Indeed, the mean, mass-averaged metallicity at the end of the fourth bursting episode has increased from the original (accreted) metallicity of Zi ∼ 0.02 to a value of Z ∼ 0.84. The nuclei in the envelope with the largest mass fractions are 60Ni (0.29), 64Zn (0.14), 4He (0.11), 32S (0.09), and 56Ni (0.06). A mass-averaged 12C yield of ∼0.02 is obtained at the end of the fourth burst, not enough to power a superburst (which requires X(12C)min ∼ 0.1 at the envelope base; see Cumming & Bildsten 2001; Strohmayer & Brown 2002; Brown 2004; Cooper & Narayan 2005; Cumming 2005; Cooper & Narayan 2006). The corresponding nucleosynthetic endpoint (defined by the heaviest isotope with a mass fraction Xi > 10−9) is found around 100Pd.
Table 10. Mean Mass Fractions of the Envelope at the End of the Fourth Burst, for Stable Nuclides and Those with Half Lives over 1 hr and Mass Fractions Xi > 10−9
| Nucleus | Model A | Model B | Model C |
|---|---|---|---|
| 1H | 3.2 × 10−2 | 4.9 × 10−2 | 4.4 × 10−2 |
| 4He | 9.7 × 10−2 | 1.1 × 10−1 | 1.0 × 10−1 |
| 12C | 1.5 × 10−2 | 1.9 × 10−2 | 1.7 × 10−2 |
| 13C | 1.3 × 10−4 | 1.5 × 10−4 | 1.3 × 10−4 |
| 14N | 7.8 × 10−4 | 8.4 × 10−4 | 7.6 × 10−4 |
| 15N | 9.3 × 10−4 | 1.0 × 10−3 | 8.2 × 10−4 |
| 16O | 2.1 × 10−4 | 2.6 × 10−4 | 2.5 × 10−4 |
| 17O | 1.1 × 10−6 | 8.2 × 10−6 | 6.6 × 10−6 |
| 18O | 1.7 × 10−5 | 7.0 × 10−6 | 9.8 × 10−6 |
| 18F | 3.6 × 10−5 | 1.9 × 10−5 | 2.5 × 10−5 |
| 19F | 4.7 × 10−5 | 4.5 × 10−5 | 3.5 × 10−5 |
| 20Ne | 1.6 × 10−4 | 4.2 × 10−4 | 3.7 × 10−4 |
| 21Ne | 2.5 × 10−6 | 4.3 × 10−6 | 4.8 × 10−6 |
| 22Ne | 6.6 × 10−6 | 2.5 × 10−5 | 1.8 × 10−5 |
| 22Na | 6.0 × 10−4 | 6.8 × 10−4 | 9.0 × 10−4 |
| 23Na | 3.8 × 10−5 | 1.9 × 10−4 | 1.2 × 10−4 |
| 24Mg | 4.1 × 10−4 | 1.4 × 10−3 | 8.9 × 10−4 |
| 25Mg | 5.0 × 10−4 | 1.6 × 10−3 | 1.1 × 10−3 |
| 26Mg | 1.1 × 10−3 | 1.0 × 10−3 | 1.1 × 10−3 |
| 26Alg | 1.3 × 10−5 | 1.3 × 10−4 | 6.6 × 10−5 |
| 27Al | 3.9 × 10−4 | 7.0 × 10−4 | 7.8 × 10−4 |
| 28Si | 5.5 × 10−3 | 1.6 × 10−2 | 8.8 × 10−3 |
| 29Si | 4.5 × 10−4 | 7.7 × 10−4 | 5.3 × 10−4 |
| 30Si | 2.3 × 10−3 | 3.0 × 10−3 | 3.0 × 10−3 |
| 31P | 1.2 × 10−3 | 1.7 × 10−3 | 1.4 × 10−3 |
| 32S | 8.7 × 10−2 | 9.0 × 10−2 | 7.3 × 10−2 |
| 33S | 4.3 × 10−3 | 4.6 × 10−3 | 4.0 × 10−3 |
| 34S | 1.3 × 10−2 | 1.5 × 10−2 | 1.3 × 10−2 |
| 35Cl | 1.4 × 10−2 | 6.3 × 10−3 | 7.3 × 10−3 |
| 36Ar | 1.6 × 10−2 | 7.0 × 10−3 | 7.7 × 10−3 |
| 37Cl | 3.2 × 10−6 | 2.5 × 10−6 | 1.6 × 10−6 |
| 37Ar | 1.2 × 10−3 | 7.4 × 10−4 | 7.6 × 10−4 |
| 38Ar | 9.5 × 10−3 | 6.2 × 10−3 | 6.8 × 10−3 |
| 39K | 1.5 × 10−2 | 1.1 × 10−2 | 1.1 × 10−2 |
| 40Ca | 5.7 × 10−3 | 4.6 × 10−3 | 4.0 × 10−3 |
| 41K | 1.2 × 10−7 | 3.5 × 10−8 | 3.5 × 10−8 |
| 41Ca | 6.0 × 10−5 | 7.3 × 10−5 | 6.3 × 10−5 |
| 42Ca | 2.2 × 10−3 | 1.5 × 10−3 | 1.4 × 10−3 |
| 43Ca | 1.4 × 10−3 | 1.3 × 10−3 | 1.2 × 10−3 |
| 43Sc | 1.3 × 10−3 | 8.2 × 10−4 | 9.5 × 10−4 |
| 44Ca | 7.8 × 10−5 | 3.1 × 10−5 | 2.2 × 10−5 |
| 44Sc | 8.8 × 10−5 | 2.7 × 10−5 | 4.5 × 10−5 |
| 44Ti | 7.4 × 10−4 | 6.8 × 10−4 | 5.7 × 10−4 |
| 45Sc | 9.6 × 10−5 | 1.3 × 10−4 | 8.9 × 10−5 |
| 45Ti | 7.5 × 10−5 | 9.7 × 10−5 | 9.7 × 10−5 |
| 46Ti | 3.3 × 10−3 | 2.5 × 10−3 | 2.1 × 10−3 |
| 47Ti | 9.8 × 10−4 | 8.6 × 10−4 | 7.1 × 10−4 |
| 48Ti | 3.5 × 10−6 | 3.2 × 10−6 | 2.1 × 10−6 |
| 48V | 3.8 × 10−4 | 3.9 × 10−4 | 2.6 × 10−4 |
| 48Cr | 1.9 × 10−3 | 2.0 × 10−3 | 1.7 × 10−3 |
| 49Ti | 6.7 × 10−7 | 7.9 × 10−7 | 7.2 × 10−7 |
| 49V | 1.1 × 10−3 | 1.4 × 10−3 | 1.2 × 10−3 |
| 50Cr | 3.4 × 10−3 | 2.9 × 10−3 | 2.4 × 10−3 |
| 51V | 3.4 × 10−5 | 3.5 × 10−5 | 2.7 × 10−5 |
| 51Cr | 6.7 × 10−3 | 6.1 × 10−3 | 5.2 × 10−3 |
| 52Cr | 6.9 × 10−5 | 9.2 × 10−5 | 6.5 × 10−5 |
| 52Mn | 2.9 × 10−3 | 4.8 × 10−3 | 3.2 × 10−3 |
| 52Fe | 6.9 × 10−3 | 1.2 × 10−2 | 9.3 × 10−3 |
| 53Mn | 7.7 × 10−4 | 1.1 × 10−3 | 7.9 × 10−4 |
| 54Fe | 2.0 × 10−3 | 1.7 × 10−3 | 1.3 × 10−3 |
| 55Mn | 1.8 × 10−7 | 1.5 × 10−7 | 1.2 × 10−7 |
| 55Fe | 1.2 × 10−3 | 1.1 × 10−3 | 8.4 × 10−4 |
| 55Co | 4.7 × 10−3 | 4.1 × 10−3 | 3.4 × 10−3 |
| 56Fe | 7.2 × 10−6 | 3.6 × 10−6 | 3.2 × 10−6 |
| 56Co | 3.8 × 10−3 | 2.1 × 10−3 | 1.9 × 10−3 |
| 56Ni | 1.4 × 10−1 | 6.3 × 10−2 | 6.0 × 10−2 |
| 57Fe | 4.7 × 10−7 | 1.9 × 10−7 | 1.6 × 10−7 |
| 57Co | 4.7 × 10−4 | 2.6 × 10−4 | 1.5 × 10−4 |
| 57Ni | 8.5 × 10−3 | 3.3 × 10−3 | 2.1 × 10−3 |
| 58Ni | 4.2 × 10−3 | 2.5 × 10−3 | 1.6 × 10−3 |
| 59Ni | 5.5 × 10−3 | 4.1 × 10−3 | 2.7 × 10−3 |
| 60Ni | 2.6 × 10−1 | 2.9 × 10−1 | 2.9 × 10−1 |
| 61Ni | 1.6 × 10−3 | 2.7 × 10−3 | 1.5 × 10−3 |
| 61Cu | 1.1 × 10−3 | 3.8 × 10−3 | 2.8 × 10−3 |
| 62Ni | 4.3 × 10−4 | 5.3 × 10−4 | 3.1 × 10−4 |
| 62Zn | 7.9 × 10−4 | 1.7 × 10−3 | 1.1 × 10−3 |
| 63Cu | 2.4 × 10−3 | 3.1 × 10−3 | 2.3 × 10−3 |
| 64Zn | 1.4 × 10−1 | 1.4 × 10−1 | 1.7 × 10−1 |
| 65Cu | 7.5 × 10−7 | 1.5 × 10−6 | 1.2 × 10−6 |
| 65Zn | 1.2 × 10−3 | 2.8 × 10−3 | 2.4 × 10−3 |
| 66Zn | 2.2 × 10−4 | 4.0 × 10−4 | 3.3 × 10−4 |
| 66Ga | 4.7 × 10−4 | 1.0 × 10−3 | 8.1 × 10−4 |
| 66Ge | 3.3 × 10−4 | 8.7 × 10−4 | 8.4 × 10−4 |
| 67Ga | 8.0 × 10−4 | 1.4 × 10−3 | 1.3 × 10−3 |
| 68Ge | 4.4 × 10−2 | 4.7 × 10−2 | 5.9 × 10−2 |
| 69Ge | 9.5 × 10−4 | 2.3 × 10−3 | 2.3 × 10−3 |
| 70Ge | 2.9 × 10−4 | 8.1 × 10−4 | 7.5 × 10−4 |
| 71As | 4.5 × 10−4 | 9.9 × 10−4 | 1.1 × 10−3 |
| 72Se | 1.4 × 10−2 | 1.6 × 10−2 | 2.2 × 10−2 |
| 73Se | 4.8 × 10−4 | 1.3 × 10−3 | 1.4 × 10−3 |
| 74Se | 2.7 × 10−4 | 6.3 × 10−4 | 7.3 × 10−4 |
| 75Br | 2.3 × 10−4 | 6.7 × 10−4 | 7.7 × 10−4 |
| 76Kr | 4.9 × 10−3 | 6.1 × 10−3 | 9.2 × 10−3 |
| 77Kr | 3.0 × 10−4 | 7.8 × 10−4 | 1.0 × 10−3 |
| 78Kr | 1.9 × 10−4 | 5.4 × 10−4 | 7.2 × 10−4 |
| 79Kr | 1.3 × 10−4 | 3.5 × 10−4 | 4.8 × 10−4 |
| 80Sr | 1.8 × 10−3 | 2.5 × 10−3 | 4.1 × 10−3 |
| 81Rb | 2.2 × 10−4 | 5.5 × 10−4 | 8.5 × 10−4 |
| 82Sr | 2.6 × 10−4 | 7.5 × 10−4 | 1.1 × 10−3 |
| 83Sr | 1.7 × 10−4 | 4.3 × 10−4 | 7.6 × 10−4 |
| 84Sr | 6.8 × 10−5 | 3.8 × 10−4 | 4.6 × 10−4 |
| 85Y | 1.9 × 10−4 | 4.6 × 10−4 | 6.9 × 10−4 |
| 86Zr | 2.1 × 10−4 | 6.3 × 10−4 | 9.8 × 10−4 |
| 87Zr | 1.6 × 10−4 | 5.4 × 10−4 | 9.4 × 10−4 |
| 88Zr | 2.5 × 10−4 | 2.8 × 10−4 | 7.3 × 10−4 |
| 89Nb | 6.5 × 10−4 | 6.1 × 10−4 | 2.4 × 10−3 |
| 90Mo | 1.2 × 10−4 | 2.7 × 10−4 | 1.0 × 10−3 |
| 91Nb | 3.7 × 10−5 | 1.5 × 10−4 | 5.8 × 10−4 |
| 92Mo | 9.2 × 10−6 | 7.1 × 10−5 | 2.6 × 10−4 |
| 93Tc | 1.4 × 10−5 | 7.7 × 10−5 | 2.6 × 10−4 |
| 94Tc | 1.7 × 10−5 | 6.9 × 10−5 | 3.0 × 10−4 |
| 95Ru | 7.7 × 10−7 | 8.4 × 10−6 | 5.3 × 10−5 |
| 96Ru | 1.7 × 10−7 | 1.5 × 10−6 | 7.6 × 10−6 |
| 97Ru | 1.7 × 10−7 | 6.6 × 10−7 | 5.8 × 10−6 |
| 98Ru | 5.2 × 10−8 | 1.5 × 10−7 | 2.6 × 10−6 |
| 99Rh | 1.3 × 10−8 | 2.2 × 10−8 | 8.5 × 10−7 |
| 100Pd | 2.4 × 10−9 | 3.3 × 10−9 | 2.1 × 10−7 |
| 101Pd | 1.4 × 10−9 | ⋅⋅⋅ | 9.7 × 10−8 |
| 102Pd | ⋅⋅⋅ | ⋅⋅⋅ | 1.6 × 10−8 |
| 103Ag | ⋅⋅⋅ | ⋅⋅⋅ | 1.5 × 10−9 |
When the lower limit for the 15O(α, γ)19Ne reaction rate is adopted (Model A), peak temperatures and luminosities of Tpeak ∼ 1.1–1.3 GK and Lpeak ∼ (1–3) × 105 L☉ are found (see Table 7). Recurrence times between bursts around τrec ∼ 4.5–6 hr and ratios between persistent and burst luminosities, α ∼ 29–50, have also been obtained. All in all, these values are very similar to those found with Model B. But more important, the model exhibits quasi-periodic bursting episodes in sharp contrast with the results reported in a similar analysis by Fisker et al. (2006). In that work, the adopted lower limit on the reaction rate, which happens to lie within a factor of two from the lower limit found in the present Monte Carlo simulation, led to steady state burning of the accreted layer without bursting. With respect to nucleosynthesis, similar amounts of unburned H (0.03, by mass) and 4He (0.1) are found at the end of the fourth burst (see Table 10). The mean, mass-averaged metallicity at the end of the fourth bursting episode reached a value of Z ∼ 0.87 in this model. The most abundant nuclides in the envelope in this model are 60Ni (0.26), 64Zn (0.14), 56Ni (0.14), 4He (0.1), and 32S (0.09). A mass-averaged 12C yield of ∼0.02 is also obtained at the end of the fourth burst, while the nucleosynthetic endpoint corresponds to 101Pd.
Finally, when the upper limit for the 15O(α, γ) rate is adopted (Model C), peak temperatures and luminosities of Tpeak ∼ 1–1.3 GK and Lpeak ∼ (0.8–2) × 105 L☉ are found (with the lower value obtained for the first burst, interpreted as driven by the initial conditions; see Table 9). Recurrence times between bursts around τrec ∼ 4.5–6 hr and ratios between persistent and burst luminosities, α ∼ 27–52, have also been obtained. In summary, the results are very similar to those reported above for Model B. As for the associated nucleosynthesis, similar amounts of unburned H (0.04, by mass) and 4He (0.1) are found at the end of the fourth burst (see Table 10). The mean, mass-averaged metallicity at the end of this fourth bursting episode is Z ∼ 0.86 for this model. The most abundant species in the envelope are 60Ni (0.29), 64Zn (0.17), 4He (0.1), 32S (0.07), and 56Ni (0.06). A mass-averaged 12C yield of ∼0.02 is also obtained at the end of the fourth burst, while the nucleosynthetic endpoint corresponds now to 103Ag, slightly above the endpoints reported for Models A and B. Indeed, as shown in Table 10, there is a trend when comparing the nucleosynthesis associated with Models A, B, and C: a small increase in the final abundances of intermediate-mass and heavy elements, likely driven by the specific choice of 15O(α, γ)19Ne rate, since a larger adopted value for the rate will translate into a more effective breakout from the CNO cycles.
6. CONCLUSION
In summary, we have evaluated the available experimental data on the states in 19Ne that serve as resonances in the 15O(α, γ)19Ne reaction in Type I XRBs. Using the likelihood distributions inferred from α decay branching ratio and lifetime measurements, we calculated the thermally averaged 15O(α, γ)19Ne reaction rate via the Monte Carlo method, determining the median and 99.73% confidence level upper and lower limits on the reaction rate. At this confidence level, the uncertainty in the rate is very large, exceeding a factor of 1000 at some temperatures. Given this large uncertainty, the central value of the rate, which does not differ from the recommended rates of Caughlan & Fowler (1988) or Fisker et al. (2006) by more than a factor of three at these temperatures, is not particularly meaningful and the whole range of reaction rates allowed by experiment must be considered.
Nevertheless, with the exception of the weak nucleosynthetic trend outlined above, we conclude that variation of the 15O(α, γ)19Ne reaction rate within the present 99.73% confidence level allowed range has no substantial effect on either the burst properties or the accompanying nucleosynthesis in our models of Type I XRBs. In striking contrast to Fisker et al. (2006), we do not find that a small value of the 15O(α, γ)19Ne reaction rate at the lower limit allowed by experiment leads to steady state burning but rather to marginally more energetic bursts than are predicted with the recommended value of the reaction rate. Further astrophysical model calculations are required to resolve the apparent discrepancy between different sensitivity studies concerning the importance of the 15O(α, γ)19Ne reaction in models of Type I XRBs.
B.D. acknowledges support from the Natural Sciences and Engineering Research Council of Canada. TRIUMF receives federal funding via a contribution agreement through the National Research Council of Canada. R.H.C. acknowledges helpful discussions with Manoel Couder and Wanpeng Tan. The work of R.H.C. was supported by the U.S. National Science Foundation Grant PHY-08-22648 (JINA). This work has been partially supported by the Spanish MICINN grants AYA2010-15685 and EUI2009-04167, by the E.U. FEDER funds, and by the ESF EUROCORES Program EuroGENESIS.