ABSTRACT
The chemical abundance patterns of the oldest stars in the Galaxy are expected to contain residual signatures of the first stars in the early universe. Numerous studies attempt to explain the intrinsic abundance scatter observed in some metal-poor populations in terms of chemical inhomogeneities dispersed throughout the early Galactic medium due to discrete enrichment events. Just how the complex data and models are to be interpreted with respect to "progenitor yields" remains an open question. Here we show that stochastic chemical evolution models to date have overlooked a crucial fact. Essentially, all stars today are born in highly homogeneous star clusters and it is likely that this was also true at early times. When this ingredient is included, the overall scatter in the abundance plane [Fe/H] versus [X/Fe] (-space), where X is a nucleosynthetic element, can be much less than derived from earlier models. Moreover, for moderately flat cluster mass functions (γ ≲ 2), and/or for mass functions with a high mass cutoff (Mmax ≳ 105 M☉), stars exhibit a high degree of clumping in -space that can be identified even in relatively small data samples. Since stellar abundances can be modified by mass transfer in close binaries, clustered signatures are essential for deriving the yields of the first supernovae. We present a statistical test to determine whether a given set of observations exhibit such behavior. Our initial work focuses on two dimensions in -space, but we show that the clustering signal can be greatly enhanced by additional abundance axes. The proposed experiment will be challenging on existing 8–10 m telescopes, but relatively straightforward for a multi-object echelle spectrograph mounted on a 25–40 m telescope.
1. INTRODUCTION
The Galactic stellar halo is a vast ancient repository that takes us back to a time when dark matter collapsed into bound structures and the Galaxy was seeded for the first time. Helmi (2008) and Tolstoy et al. (2009) provide excellent overviews of the many stellar systems and fragments that inhabit the halo. These include field halo stars (Christlieb et al. 2002; Cayrel et al. 2004; Frebel et al. 2005; Cohen et al. 2007), globular clusters (Gratton et al. 2004), dwarf spheroidals (Mateo 1998; Venn et al. 2004), ultra-faint dwarf galaxies (Simon & Geha 2007; Kirby et al. 2008), stellar streams (Ibata et al. 1995; Chou et al. 2010), stellar associations (Walsh et al. 2007), and satellites to dwarf galaxies (Coleman et al. 2004; Belokurov et al. 2009). Already the chemical information arising from the most metal-poor stars is very difficult to unravel (Nomoto et al. 2005; Kirby et al. 2008). We have barely begun to understand what these systems are telling us about the sequence of events that led to the Galaxy (McWilliam et al. 2009; Freeman & Bland-Hawthorn 2002).
The first stars were unique to their time. The first stellar generations changed the universe in many ways; in particular, the chemical properties and the equation of state of the intergalactic medium. But at present there are many unknowns. Did the first stars form in isolation or in groups? Were relatively few massive stars responsible for reionization or was it triggered by the collective effect of massive star clusters? Just what are the processes that govern star formation at extremely low metallicity? Is this exclusively the domain of the most massive stars, or can substantial intermediate and low mass stars form (Tsuribe & Omukai 2006, 2008; Clark et al. 2008)? In other words, did stellar populations observable today exist before reionization (Tumlinson 2010; Okrochov & Tumlinson 2010)? The first star clusters are of great interest in that they shed light on star formation processes in the early universe (Bromm et al. 2002; Abel et al. 2002). There are few if any reliable constraints at the present time.
One of the most interesting developments in recent years is the simultaneous measurement of many elemental abundances for individual metal-poor halo stars or groups of stars (e.g., Beers & Christlieb 2005). Some of these elements, but not all, exhibit intrinsic scatter in the abundance plane [Fe/H] versus [X/Fe] that exceeds the measurement errors. While the scatter is particularly apparent in halo stars (e.g., Roederer et al. 2009), evidence is now emerging that star-to-star abundance variations exist in dwarf galaxies as well (Fulbright et al. 2004; Koch et al. 2008; Feltzing et al. 2009). The observed scatter is likely to increase now that metal poor stars are now detected below [Fe/H] = −3 (Norris et al. 2010; Starkenburg et al. 2010; Simon et al. 2010; Frebel et al. 2010). This has led numerous researchers to argue that the scatter in [X/Fe] is a tracer of an ancient inhomogeneous medium (e.g., Audouze & Silk 1995; Ryan et al. 1996; McWilliam 1997; Ishimaru & Wanajo 1999). If this interpretation is correct, we would expect that a subset of these stars is telling us something fundamental about the first stars and their yields. But not all of the stars are providing us with an unambiguous "reading" of the early enrichment of the primordial interstellar gas. For example, a significant fraction of extremely metal poor stars appear to have undergone mass transfer with a companion (Ryan et al. 2005; Lucatello et al. 2005) which undermines any attempt at inferring the progenitor yields for elements such as CNO and α elements. Binarity may partly explain why the elemental abundances of the most metal poor stars defy a clear explanation at the present time (Joggerst et al. 2010; McWilliam et al. 2009).
We now incorporate a missing ingredient into existing models of stochastic chemical evolution. In the present-day universe, most stars are born in a single burst within compact clusters and stellar fragments, rather than in isolation. This fact is well established in the local universe (Lada & Lada 2003) and is likely to be true at the time of the first stars (Clark et al. 2008). Cluster formation has an important consequence for the distribution of stars in the abundance plane. De Silva et al. (2006, 2007a,b) have shown that both old (∼10 Gyr) and intermediate-age (∼1 Gyr) open clusters are chemically homogeneous to a high degree (Δ[Fe/H] ≲0.03 dex). The open cluster Tombaugh 2 was thought to be a rare example of a chemically inhomogeneous open cluster (Frinchaboy et al. 2008), but this is contradicted by a new study that finds the stellar population to be highly homogeneous (Δ[Fe/H] ≲0.02 dex; Villanova et al. 2010). Apart from a few light elements, the same holds true for globular clusters (Gratton et al. 2004), although some systems (e.g., ωCen) show evidence for more than one burst of star formation. Interestingly, even moving groups can show the same signature of chemical homogeneity (De Silva et al. 2007a; Chou et al. 2010; Bubar & King 2010).
Bland-Hawthorn et al. (2010) provide a condition that ensures chemical homogeneity in a young star cluster based on the surface density of the progenitor gas. They show that chemical homogeneity is expected in open clusters, globular clusters and plausibly clusters more massive than 107 M☉. This process has not been incorporated into stochastic chemical models to date. Once this is done, we arrive at an important insight that will enhance the interpretation of metal abundance distributions in individual stellar populations. The effects that we highlight can be searched for in existing and in future surveys, as we show.
A key assumption in our present work is that present-day dwarf galaxies are important sites for establishing the yields of the first stars and star clusters. This needs some clarification. While it is likely to be true that the most efficient way to identify metal-poor stars is to target dwarf galaxies, a low value of [Fe/H] is no guarantee that a star is ancient since it may simply reflect environmental conditions (e.g., low star formation efficiency, weak gravity field). Published numerical simulations are unclear on whether the most ancient stars are solely the preserve of the inner bulge (White & Springel 2000; Bland-Hawthorn & Peebles 2006) or spread over the entire Galaxy (Scannapieco et al. 2006; Brook et al. 2007). But it is now well established that the bulge, the halo and all dwarf galaxies comprise stellar populations that are 10 Gyr or older, equivalent to a formation redshift of z ≳ 2 (e.g., Tolstoy et al. 2009). The relative fractions of dwarf populations that formed before, during, or after the reionization epoch is an open question. We are therefore at liberty to explore new observational constraints on the nature of the first stars and star clusters.
In Section 2, we present evidence for homogeneous star clusters in the local universe and argue that the same should be true for their high-redshift counterparts. In Section 3, we briefly outline the inhomogeneous chemical evolution models that have been developed to date. In Section 4, we introduce a revised stochastic model of star formation in dwarf galaxies that incorporates the "homogeneity" condition described by Bland-Hawthorn et al. (2010), and show the predictions of the revised model in view of the earlier work. In Section 5 and in the Appendix, we introduce cluster finding algorithms for both large and small data sets, and demonstrate how the effects of clustering may already be visible in existing observations. We also explore the longer term prospect offered by a multi-object echelle spectrograph on an extremely large telescope (ELT). The conclusions are presented in Section 6.
2. HOMOGENEOUS STAR CLUSTERS
Before revisiting stochastic chemical evolution models, we review the key arguments presented in Bland-Hawthorn et al. (2010) on the conditions under which star clusters are expected to be highly homogeneous in most elements, as observed for local star clusters (Section 1). We then extend these arguments to clusters at low metallicity.
As a star-forming cloud assembles, turbulent diffusion within it will homogenize its chemical composition (Murray & Lin 1990). For clouds whose turbulent motions are primarily on large scales (as is the case for all local molecular clouds—Heyer & Brunt 2004), Bland-Hawthorn et al. (2010) show that the time required for this process to smooth out a composition gradient on the size scale of the cloud is roughly tcr = L/σ, where tcr is the cloud crossing time, L is its size, and σ is its velocity dispersion. Smaller-scale gradients are erased more quickly, with the diffusion time varying as the square of the (normalized) characteristic size scale. Since tcr is comparable to or smaller than the time scale over which star formation takes place, clouds will homogenize as they assemble, and will be pushed away from homogeneity only if supernovae (SNe) occur during the star formation process, before the cloud disperses. The time required for a very massive star to evolve from formation to explosion defines the SN time scale, tSN ≈ 3 Myr, and we only expect star clusters to be homogeneous if they are assembled on time scales shorter than tSN.
To determine under what conditions this requirement is satisfied, we must compare tSN to the cluster formation time scale tform. There is considerable debate over this time scale, so for our purposes we will adopt the longest, most conservative proposed time scale of 4 tcr (Tan et al. 2006). Since
for a cloud of mass M, column density Σ, and virial ratio αvir; observed clouds have αvir ≈ 1.5 (McKee & Ostriker 2007). For convenience, we write the final stellar mass of a cluster as M* =  M, where
M, where  is the star formation efficiency. Both observational and theoretical arguments suggest
is the star formation efficiency. Both observational and theoretical arguments suggest  ≈ 0.2 independent of M (Lada & Lada 2003; Fall et al. 2010). Thus the condition that tform ≈ 4tcr < 2tSN (where the factor of 2 arises because the typical star forms halfway through the formation process) is satisfied only if
≈ 0.2 independent of M (Lada & Lada 2003; Fall et al. 2010). Thus the condition that tform ≈ 4tcr < 2tSN (where the factor of 2 arises because the typical star forms halfway through the formation process) is satisfied only if
where M*,5 = M*/(105 M☉) and Σ0 = Σ/(1gcm−2), and we have adopted fiducial values of  = 0.2 and αvir = 1.5. Star-forming regions within the galaxy have Σ0 ≈ 1 g cm−2 independent of mass (Fall et al. 2010). Globular clusters today have somewhat higher values of Σ, although it is unclear if this reflects the conditions under which they formed, or is the result of dynamical evolution since their formation. Regardless, this analysis suggests that clusters with masses up to ∼105 M☉ should be chemically uniform and maybe much higher if systems form with the nuclear densities observed in today's globular clusters (Bland-Hawthorn et al. 2010).
= 0.2 and αvir = 1.5. Star-forming regions within the galaxy have Σ0 ≈ 1 g cm−2 independent of mass (Fall et al. 2010). Globular clusters today have somewhat higher values of Σ, although it is unclear if this reflects the conditions under which they formed, or is the result of dynamical evolution since their formation. Regardless, this analysis suggests that clusters with masses up to ∼105 M☉ should be chemically uniform and maybe much higher if systems form with the nuclear densities observed in today's globular clusters (Bland-Hawthorn et al. 2010).
There are few observational constraints on the existence of star clusters in extremely metal poor gas. In the nearby universe, clear evidence for star clusters at [Fe/H]≈ −1.7 is observed in the most metal-poor, blue compact dwarf galaxy I Zw 18 (Izotov & Thuan 2004). Globular clusters are known to exist down to [Fe/H]≈ −2.4 (Gratton et al. 2004). We now argue that the above estimate for the uniform mass limit is likely to apply at metallicities as low as [Fe/H] ≈ −5.
Low metallicity can change the star formation process in two ways that are relevant to the chemical signatures of the resulting stars. First, a change in metallicity can affect the way star-forming clouds fragment; if there is no fragmentation down to sub-solar masses below a certain metallicity, then no stars below that metallicity will survive to the present day. Fragmentation of low metallicity gas has received extensive attention in the literature, which we will only summarize here. The main point relevant for our purposes is that, when dust cooling is considered, gas is able to fragment to sub-solar masses even at metallicities at low as ∼10−6 of the solar abundance (Clark et al. 2008; Schneider & Omukai 2010). Once fragmentation is possible, turbulence naturally generates a mass spectrum of fragments with a slope comparable to the Salpeter slope dn/dm ∝ m−2.35 (Padoan & Nordlund 2002; Hennebelle & Chabrier 2008), and the properties of the turbulence do not depend on the redshift or the metallicity. Alternately, Clark et al. (2009) have proposed that competitive accretion processes would generate a universal mass spectrum, although doubts have been raised about whether this process in fact operates on both theoretical (Krumholz et al. 2005) and observational (André et al. 2007) grounds. In either case, however, we expect there to be some sub-solar mass stars formed that can survive to the present day.
Given that small stars form at low metallicity, we can then ask whether our conclusions about cluster chemical homogeneity will continue to apply in this regime. A failure of homogeneity could occur either if clouds did not homogenize during star cluster formation, or if the cloud properties changed such that the cluster formation time became longer than the SN time scale. The former is unlikely because the homogenization time is comparable to the crossing time, and it is implausible that any star formation process could take place in less time. The latter would require that protocluster gas clouds all have surface densities significantly below ∼0.1 g cm−2 which is highly unlikely to be true. However this would imply that the star-forming clouds had surface densities at or below the mean surface density of observed high redshift galaxies (e.g., Genzel et al. 2006), which is implausible. We therefore conclude that homogeneity should continue to apply as well.6
3. EXISTING INHOMOGENEOUS CHEMICAL EVOLUTION MODELS
3.1. A Statistical Treatment
Many authors have attempted to explain the declining scatter in elemental abundances with increasing [Fe/H] in terms of star formation within an interstellar medium (ISM) that is enriched by a succession of SN events (Ishimaru & Wanajo 1999; Shigeyama & Tsujimoto 1998; Raiteri et al. 1999; Argast et al. 2000, 2004; Wasserburg & Qian 2000; Karlsson & Gustafsson 2001, 2005; Qian 2000, 2001; Travaglio et al. 2001; Fields et al. 2002). In the [Fe/H] versus [X/Fe] plane,7 the scatter in [X/Fe] is due to two or more classes of SN that produce distinct yields of [X/Fe]. In these stochastic models, the scatter converges roughly quadratically to a mean value of [X/Fe] given by the SN yields weighted by the initial mass function (IMF). In its simplest form, this behavior is driven by the number of SN events (nSN), such that [Fe/H] = [Fe/H]min + log nSN, where [Fe/H]min is the minimum allowed metallicity. In other words, if [Fe/H]min = −5 consistent with the most metal-poor stars to date (e.g., Frebel et al. 2010), it takes 105 SNe to enrich a gas parcel to solar abundance. An example of this behavior is presented in Bland-Hawthorn & Freeman (2004; Figure 3) where the number of SNe are indicated.
If the interpretation of declining inhomogeneity is broadly correct, we can hope to learn about the yields of the first SNe responsible for the enrichment (Fields et al. 2002). In other words, if the scatter in [X/Fe] is due to a high-yield source (class A) and a low-yield source (class B), an individual star with known [Fe/H] has a fraction of fA = nA/nSN progenitors and fB = nB/nSN progenitors of a total progenitor population of nSN = nA + nB SNe. We can simulate this with a random variable f = fA drawn from the beta distribution function,
defined for f ∈ [0, 1] such that ∫10ξ df = 1 and where Γ is the gamma function. The quantities α and β describe the yields of the two populations, such that -1) and -1). The mean, variance and higher moments of the normalized distribution ξ(f) depend only on α and β.
Equation (3) has several remarkable properties that are useful for describing the declining influence of chemical inhomogeneities in the early ISM. The mean is given by such that is the mean of the distribution ξ(fA). The variance is given by σ2 = αβ(α + β)−2(α + β + 1)−1 which leads to a scatter that declines as σ ∝ n−0.5SN as expected.8 Even initially skewed distributions in ξ converge to the normal distribution () in the limit of high nSN, as expected from the central limit theorem.
Four realizations of the beta distribution (i.e., no clustering) are presented in Figure 1; a total of n* = 3000 points was used for each simulation distributed in [Fe/H] according to Figure 2 (see Section 5). The log ξ distribution can be renormalized trivially to match a given set of [Fe/H] versus [X/Fe] observations (e.g., Fields et al. 2002). The beta distribution ξ is everywhere continuous in fA, and therefore fB, except in the limit of small nA or nB. This recognizes the fact that, as stated by Fields et al. (2002), "a given parcel of ISM gas and dust can be enriched to different degrees by the ancestors it had." But in the limit of small nA or nB, discreteness effects may exist. Stars with very few prior enrichments, if they can be identified, provide crucial information on the progenitor yields of class A or B sources (e.g., Shigeyama & Tsujimoto 1998; Karlsson & Gustafsson 2001; Ballero et al. 2006), but within the domain of the statistical model, these are rare events and may be difficult to find unambiguously. This is an issue we return to in Section 5. At high [Fe/H], when new sources of metals become dominant (e.g., type Ia SNe, asymptotic giant branch stars [AGBs]), the simple description in Equation (3) breaks down.
Figure 1. Four realizations of the beta distribution in Equation (3). The vertical axis log ξ can be trivially rescaled to match the observed scatter in [X/Fe]. The abundance scatter declines quadratically (in linear space) as expected (see Section 3.1).
Download figure:
Standard image High-resolution imageFigure 2. Metallicity distribution function (MDF) for the stochastic chemical evolution models presented in Figures 3 and 4. The main plot shows the log of the MDF and the inset is the more conventional linear MDF. The quantity f* is the fraction of stars that fall within each [Fe/H] bin (1 dex). The dashed curve shows the gradient defined by which illustrates that the fraction of stars in each [Fe/H] bin increases roughly by a factor of 10 as the metallicity increases up to the turnover at .
Download figure:
Standard image High-resolution imageTo recap, the model described by Equation (3) assumes that a star with a given [Fe/H] has been enriched to different degrees by its type A and type B ancestors which is considered to be a continuous rather than a discrete process. Equation (3) is used to generate a distribution of possible values of fA at a constant value of [Fe/H] or equivalently nSN. More complex models show that there is generally no simple relation between fA and [Fe/H] (e.g., Qian 2001; Bland-Hawthorn & Freeman 2004).
We note already from Figure 1 that spurious groupings (false positives) are inevitable, particularly when the data points are convolved with typical errors of 0.1 dex psf for differential abundance analysis. The importance of the beta distribution in Equation (3) is that it enables us to efficiently generate large numbers of unbiased realizations (≳103) of the theoretical abundance plane, something that is infeasible with full-blown chemical modeling. These are required to calibrate the statistical properties of our group-finding algorithm in Section 5. This step is necessary if we are to identify significant groups against a rapidly changing background, as observed in Figure 1. Clusters at low [Fe/H] will have a higher level of significance than abundance groupings at higher [Fe/H] (cf. Karlsson et al. 2008) and we need to be able to identify groups with smaller number statistics.
But first we must consider more complex treatments of stochastic chemical evolution that will allow us to include the effects of clustering during star formation.
3.2. Inhomogeneous Stochastic Model
The chemical evolution model that most resembles our new work is Argast et al. (2000, 2004). Their model was computed over a volume (2.5 kpc)3 for a uniform gas mass of 108 M☉ at a resolution of (50 pc)3, such that they were sensitive to chemical inhomogeneities on mass scales as low as 103 M☉. A distinct feature of the Argast model is that star formation mostly occurs in the expanding shell of material swept up by the SN shock front. They make the simplifying assumption that [X/Fe] is determined by the SN yield such that [Fe/H] is a combination of the SN yield and the swept-up ISM, and that the shell is everywhere fully mixed.
There are several problems with this assumption. First, as far as we are aware, there is no compelling evidence for star formation occurring in supernova remnant (SNR) shells. The closest one gets are some studies of the Large Magellanic Cloud and the Galaxy (Yamaguchi et al. 1999, 2001) which conclude that maybe ∼10% of star forming regions today appear to be triggered by local SN events. There is a clear distinction that must be made. If the star formation occurred in collapsing massive clouds triggered by the passing shock wave, rather than in the swept up shell, we would still expect these star clusters to be highly homogeneous.
Second, core-collapse SNe are inherently asymmetric due to the nature of the explosion mechanism due to stellar rotation, magnetic fields, and so on (Wang & Wheeler 2008). Asymmetric ejections from these SNe are well supported by observations (q.v. Maund et al. 2009). Therefore, the remnant shells are highly unlikely to be chemically homogeneous, again supported by X-ray observations of nearby SNRs (Wang & Wheeler 2008). Asymmetric enrichment would have led to even larger spread in the elemental abundances, thereby invalidating their model comparisons.
Thirdly, our new homogeneity condition, supported by observation, is essentially independent of the original gas distribution. This constitutes a smoothing scale in mass below which metallicity variations cannot occur, thereby suppressing the amount of scatter observed in the abundance plane (cf. Argast et al. 2004).
We now introduce our revised chemical evolution model which incorporates the onset of chemically homogeneous star clusters.
4. REVISED CHEMICAL EVOLUTION MODEL
4.1. Initial Cluster Mass Function
In order to derive the impact of star clusters on the abundance plane, we must consider the progenitor mass distribution of star clusters. It is now well established that star clusters have a range of masses that extend from a maximum mass (Mmax) to a minimum mass (Mmin). The form of the birth distribution is known as the initial cluster mass function (ICMF) and is assumed to have the form
The observations may support a universal slope of γ ≈ 2 in all environments, i.e., equal mass per logarithmic bin (Fall et al. 2005, 2009; Lada & Lada 2003; Elmegreen 2010). In this picture, the only parameter that does appear to vary at all between galaxies today is Mmax, which can be represented schematically as a Schechter function-like cutoff in the ICMF, although there is no good reason to prefer this functional form over a simple truncation.
A power law is logarithmically divergent at both low and high masses, so it must be truncated somewhere. At low masses, the truncation is due to the discreteness of stellar masses—the smallest cluster is simply one star. At large masses, there must also be a truncation. For this reason, and because the molecular cloud mass function (as opposed to the cluster mass function) is observed to have a non-trivial truncation, there is likely to be a maximum cluster mass, and that it varies depending on galactic environment. In disk galaxies, a possible explanation is that the truncation mass is of order the Toomre mass in the galactic disk (Toomre 1964; Escala & Larson 2008), which is ∼106 M☉ for the Milky Way, but is significantly larger for present-day starburst/merger galaxies (Larsen 2009) and their high-redshift counterparts (Genzel et al. 2006; Förster-Schreiber et al. 2009). The situation in spheroidal galaxies is much less clear but the common occurrence of globular clusters indicates that massive cluster formation must take place (Elmegreen 2010).
4.2. Stochastic Chemical Evolution
We take as our starting point the stochastic chemical enrichment model presented in Karlsson (2005, 2006) and Karlsson et al. (2008). This model is now updated to include the homogenizing processes that must occur during the formation of star clusters (Section 2). But in order to do this, two additional mixing processes must be accounted for. First, since stars within clusters show no evidence of scatter in chemical abundance ratios, the gas involved in the formation of a cluster must be homogenized prior to, and stay homogenized during, the formation of the individual stars. We include a mixing process to ensure that this is always true during the cloud collapse and cluster formation phase. Second, since massive stars are short lived (τ⋆ ≲ 20 Myr) they will explode as SNe before the cluster has dispersed. Assuming that the cluster is unbound and that the intrinsic velocity dispersion of the stars in the cluster is ∼1 km s−1, massive stars will, on average, be ∼20 pc apart when they go off as SNe. This is less than the typical size (∼100 pc) of an SNR as it merges with the ambient medium. (e.g., Ryan et al. 1996). Therefore, we assume that the ejecta of all SNe formed within a single cluster enrich the ISM collectively with a mixing mass that scales linearly with the total energy output of the clustered SNe. These two processes, which produce additional averaging of newly synthesized material before a new generation of stars is formed, have not been considered in earlier models.
The mixing volume, Vemix, of each chemical enrichment event is given as a power-law expression. The present model is somewhat simplified as we suppress the continuous mixing due to the bulk random motions in the turbulent ISM. Without the time-dependent turbulent diffusion term (cf. Karlsson et al. 2008, Equation (1)), Vmix reduces to
where
ρ is the density of the ISM and Mdil(k) is the dilution mass of the ejecta of a number k (≡nSN) of SNe as they merge with the ambient medium (e.g., Cioffi et al. 1988). Here, we assume that the total dilution mass for the ejecta of multiple SNe exploding in a cluster is proportional, on average, to the total energy released by the SNe associated with that cluster, such that
where Mjsw is the mass swept up by individual SNe assuming it explodes in isolation. In order to introduce a small amount of randomness, log(Msw) is drawn from a normal distribution centred on log(Msw) = 5 with a width of 0.25. Note that this mixing process is denoted a single enrichment event, even though it may involve enrichment by multiple SNe.
In addition to this mixing, there is also a mixing volume associated with the formation of the cluster during the collapse of the molecular cloud, Vfmix, such that
where M is the mass of the molecular cloud associated with the star cluster. Within this volume, everything is assumed to be thoroughly mixed before stars are allowed to form.
In our models, we explore the range 1 ≲ γ ≲ 2.5 (e.g., Kroupa & Boily 2002), between clusters of mass (Mmin, Mmax) = (5 M☉, 5 × 104 M☉), which is our fiducial mass range (Larsen 2009; Portegies Zwart et al. 2010). We adopt a simple scaling relation between the cluster mass and the mass of the parent molecular cloud, such that M = M*/ , where we adopt a star formation efficiency of
, where we adopt a star formation efficiency of  = 0.2 (see Section 2). Similarly, the stellar initial mass function (IMF) is governed by
= 0.2 (see Section 2). Similarly, the stellar initial mass function (IMF) is governed by
For simplicity, α = 2.35, which recovers the Salpeter IMF. The range of stellar masses is set to 0.1 ⩽ m/M☉ ⩽ 100 and ϕ0 = 6.03 × 10−2 M☉1.35.
Formally, the average number of clusters contributing to the chemical enrichment in a random point in space can be expressed by the parameter μe, here given by
where is the fraction of clusters in which k SNe explode, while ucl(t') is the formation rate of star clusters, closely related to the star formation rate and Vemix(k = 0) = 0. The value of kmax is set by the IMF and the upper mass limit of star clusters. On average, 270 massive stars explode as SNe in a cluster of mass 5 × 104 M☉. Such a cluster will not form more than 320 SNe at the 3σ level. We set kmax = 400 to be on the safe side.
Now, if we make the simplifying assumption that star clusters are randomly distributed in space (i.e., not themselves clustered), the probability of finding a region in space enriched by κ events, i.e., κ clusters producing one or more SNe, at time t is given by the Poisson distribution
To follow the chemical enrichment in a typical dwarf galaxy, we assume a simulation box of 1.6 kpc on a side, with an initial, constant particle density of n0 = 1 cm−3, corresponding to a gas density of ρ0 = 2.06 × 10−24 g cm−3. The initial mass of baryons in the box is thus 3.1 × 107 M☉ which is sufficient to make the largest star clusters considered in this work. The initial metallicity is set to Z = 0. In the box, star clusters are allowed to form from collapsing molecular clouds. The molecular clouds are distributed randomly within the box and the masses of the corresponding clusters are distributed according to Equation (4). During the collapse of a molecular cloud, the volume, Vfmix, of gas corresponding to the mass of the cloud is made chemically homogeneous. The stars of the cluster will all have chemical abundances equal to those of the parent cloud. The number of massive stars, k, in the cluster that will explode as SNe is, again, determined by the Poisson statistics P(k, μSN), where the mean number of SNe in a cluster of a given mass is given by
where  is the star formation efficiency, M is the mass of the molecular cloud, fSN = 1.9 × 10−3 is the fraction of massive stars exploding as SNe, and is the mean stellar mass in a single stellar population. The last two parameters are determined by the IMF. For large values of μSN, the Poisson distribution approaches a normal distribution. We make use of this fact to simplify the calculations for μSN>32. In clusters where one or more SNe are formed, the ejecta of all SNe, with masses distributed according to Equation (9), are homogeneously mixed with the metals already present within the volume Vemix. The Fe-core collapse SN yields, in particular of Ca and Fe, are taken from Nomoto et al. (2006) while the yields of Eu, representing r-process elements and assumed to be formed in O–Ne–Mg core collapse SNe in the mass range 8 ⩽ m/M☉ ⩽ 10, are taken from Argast et al. (2004). In order to match the simulations with observations of metal-poor stars in the Galactic halo, the yields of Eu are doubled.
is the star formation efficiency, M is the mass of the molecular cloud, fSN = 1.9 × 10−3 is the fraction of massive stars exploding as SNe, and is the mean stellar mass in a single stellar population. The last two parameters are determined by the IMF. For large values of μSN, the Poisson distribution approaches a normal distribution. We make use of this fact to simplify the calculations for μSN>32. In clusters where one or more SNe are formed, the ejecta of all SNe, with masses distributed according to Equation (9), are homogeneously mixed with the metals already present within the volume Vemix. The Fe-core collapse SN yields, in particular of Ca and Fe, are taken from Nomoto et al. (2006) while the yields of Eu, representing r-process elements and assumed to be formed in O–Ne–Mg core collapse SNe in the mass range 8 ⩽ m/M☉ ⩽ 10, are taken from Argast et al. (2004). In order to match the simulations with observations of metal-poor stars in the Galactic halo, the yields of Eu are doubled.
In order to account for the amount of mass locked up in low-mass stars and stellar remnants and the mass lost due to star formation driven galactic outflows, a fraction, fout = 0.46, of the mass of each star-forming molecular cloud is subtracted from the total mass of the system. The gas density is decreased accordingly. Infall and mass lost via interaction with the surroundings, such as tidal and ram pressure stripping are not considered here. When the total mass and gas density of the system has been re-calculated, the next cycle begins with the formation of a new cluster. Since our focus is in the metal-poor regime, the yields of type Ia SNe and AGB stars are not considered here.
4.3. Results
The results of the clustered simulations for [Ca/Fe] and [r/Fe] with respect to [Fe/H] are presented in Figures 3 and 4, respectively. For all models, the number of simulated stars is n* ∼ 107, equivalent to a stellar mass of 3 × 106 M☉ and a luminosity of 106 L☉ assuming a Salpeter IMF; the luminosity is two times higher for a Kroupa IMF. To begin with, we do not consider the effect of distance on the observed number counts; this is treated in Section 5.2. The modeled number of stars is much larger than we can expect to obtain in nearby dwarfs, but the results provide sufficient resolution to understand the impact of the ICMF parameters. The overall distribution of the stars with metallicity is shown in Figure 2.
Figure 3. Results of the stochastic chemical evolution modeling in Section 5 for α element Ca compared to [Fe/H]. The five models from top to bottom are: (1) no clustering, (2) γ = 2.5, (3) γ = 2.0, (4) γ = 1.5, (5) γ = 1.0. The left and right hand panels are two different realizations of the same five models. The clustering in abundance space becomes very apparent at low values of γ. High values of γ are barely distinguishable from the "no clustering" distribution in (1). Note also that the scattering at a fixed value of [Fe/H] decreases dramatically with decreasing values of γ. The intrinsic dispersion within individual clusters (0.01 dex) is much less than expected in real data; more realistic models with fewer data points and increased measurement error are presented in Figure 7.
Download figure:
Standard image High-resolution imageFigure 4. Results of the stochastic chemical evolution modeling in Section 5 for r-process element (specifically Eu) compared to [Fe/H]. The vertical extent is 4 dex in [r/Fe], i.e., a fourfold increase over [Ca/Fe] in Figure 3. (The vertical and horizontal axes are presented with the correct aspect ratio in Figures 5 and 7.) The five models from top to bottom are: (1) no clustering, (2) γ = 2.5, (3) γ = 2.0, (4) γ = 1.5, (5) γ = 1.0. The left and right hand panels are two different realizations of the same five models. The clustering in abundance space becomes very apparent at low values of γ. High values of γ are barely distinguishable from the "no clustering" distribution in (1). Note also that the scattering at a fixed value of [Fe/H] decreases dramatically with decreasing values of γ. In order to make clustered points more circular, the intrinsic dispersion within individual clusters is Δ[Fe/H] = 0.01 dex and Δ[Eu/Fe] = 0.035 dex.
Download figure:
Standard image High-resolution imageThere is a clear progression moving from high γ to low γ in the occurrence of clustered abundance signatures. The high γ limit is indistinguishable from the beta (non-clustered) models. This is not unexpected since, in the limit of γ = 2.5, almost all stars are formed in small star clusters such that unique groupings in abundance space are poorly represented.
As γ decreases, the clustering increases markedly but at the expense of the dispersion in [X/Fe]. In the limit of γ = 1, the vertical spread has vanished over all [Fe/H] with little or no abundance spread in [X/Fe]. While γ = 1 is smaller than what is observed, it is in fact a useful surrogate for demonstrating the impact of a higher maximum cloud mass Mmax for larger γ values. For example, in Figure 5, we show the result of running γ = 1.5 and γ = 2.0 models with Mmax ≈ 106 M☉. We see how the high mass cutoff at high γ mimics the behavior of a lower value of γ: the vertical scatter is greatly reduced, and groupings are seen to extend to lower [Fe/H].
Figure 5. Results of the stochastic chemical evolution modeling in Section 5 for the 2D space ([Fe/H], [r/Fe]). The top two panels are repeated from Figure 4 for which γ = 1.5 (left) and γ = 2.0 (right), both with a high mass cutoff Mmax = 5.0 × 104 M☉. The bottom two panels use γ = 1.5 (left) and γ = 2.0 (right) but with a high mass cutoff Mmax = 1.0 × 106 M☉, twenty times higher than was used for the upper panels. Note how the high mass cutoff at high γ mimics the behavior of a lower value of γ: the distribution is everywhere flattened in the vertical direction, and groupings are seen to extend to lower [Fe/H]. This behavior is particularly apparent in the left-hand figures.
Download figure:
Standard image High-resolution imageIn Figure 6, we show the cumulative fraction of stars and the integrated light as a function of stellar absolute magnitude for the model dwarf galaxy. In Table 1, we give a rough breakdown of how many stars are expected for the dwarf galaxy as a function of stellar apparent magnitude, distance and metallicity. We consider V = 16 and V = 18 to be the bright and faint limit of an 8 m class experiment; these magnitude brackets become V = 20 and V = 22 on an ELT (Bland-Hawthorn et al. 2010).
Figure 6. Top: cumulative fraction of stars brighter than a given stellar absolute magnitude MV for a Salpeter (lower) and Kroupa (upper) IMF. The high and low stellar mass cutoffs for both IMFs are 0.1 M☉ and 100 M☉. The stellar population has a mass of 3 × 106 M☉ and we use the Padova isochrones (see the text) for a 12 Gyr old single burst, metal-poor population. Bottom: integrated light from this same population brighter than a given stellar absolute magnitude MV.
Download figure:
Standard image High-resolution imageTable 1. Log of the Expected Numbers of Stars as a Function of V mag for an Old, Metal Poor Dwarf Spheroidal (see Figure 2) with 107 Stars (Stellar Mass ≈ 3 × 106 M☉) at Distances of 10, 30 and 100 kpc (Column 1)
| [Fe/H] | Salpeter | Kroupa | ||||||
|---|---|---|---|---|---|---|---|---|
| −5:−4 | −4:−3 | −3:−2 | −2:−1 | −5:−4 | −4:−3 | −3:−2 | −2:−1 | |
| V = 16 | ||||||||
| 10 | 0.7 | 1.9 | 3.0 | 3.5 | 1.0 | 2.2 | 3.3 | 3.8 |
| 30 | ⋅⋅⋅ | 0.8 | 1.9 | 2.4 | ⋅⋅⋅ | 1.1 | 2.2 | 2.7 |
| 100 | ⋅⋅⋅ | - | 0.4 | 1.0 | ⋅⋅⋅ | - | 0.7 | 1.3 |
| V = 18 | ||||||||
| 10 | 1.1 | 2.3 | 3.4 | 3.9 | 1.4 | 2.6 | 3.7 | 4.2 |
| 30 | 0.7 | 1.9 | 3.0 | 3.5 | 0.9 | 2.2 | 3.2 | 3.8 |
| 100 | ⋅⋅⋅ | 0.6 | 1.7 | 2.2 | ⋅⋅⋅ | 0.9 | 2.0 | 2.5 |
| V = 20 | ||||||||
| 10 | 2.2 | 3.4 | 4.5 | 5.0 | 2.5 | 3.7 | 4.8 | 5.3 |
| 30 | 1.0 | 2.2 | 3.3 | 3.8 | 1.3 | 2.5 | 3.6 | 4.1 |
| 100 | 0.1 | 1.3 | 2.4 | 2.9 | 0.4 | 1.6 | 2.7 | 3.2 |
| V = 22 | ||||||||
| 10 | 2.8 | 4.0 | 5.1 | 5.6 | 3.0 | 4.3 | 5.3 | 5.8 |
| 30 | 2.0 | 3.3 | 4.3 | 4.8 | 2.3 | 3.5 | 4.6 | 5.1 |
| 100 | 0.9 | 2.1 | 3.2 | 3.7 | 1.2 | 2.4 | 3.4 | 4.0 |
Notes. Columns 2–5 are the star counts for a Salpeter IMF in four metallicity bins; columns 6–9 are the counts for a Kroupa IMF in the same bins determined from the MDF in Figure 2. The four metallicity bins are [Fe/H] = (−5: − 4), (−4: − 3), (−3: − 2), (−2: − 1); dashes indicate that no stars are expected.
Download table as: ASCIITypeset image
In the next section, we analyze these simulations using a group finder in order to provide an objective assessment of the amount of measurable clustering in the limit of high and low n* that we can expect. We apply this analysis for different [Fe/H] cutoffs since, as we have seen, the abundance plots become crowded as [Fe/H] increases.
5. CLUSTERING IN -SPACE: A STATISTICAL TREATMENT
5.1. Group Finding for Large n*
In order to investigate the clustering in abundance space (defined by [Fe/H] and [Ca/Fe] or [r/Fe] abundances), we use the density-based hierarchical clustering algorithm EnLink (Sharma & Johnston 2009). The method is statistically objective and robust in its application; the method is highly efficient and does not use pixellation or binning.
EnLink is based on the fact that a system having more than one group in a data set will have peaks and valleys in the density distribution. A peak in a density distribution identifies a cluster and the set of points which can "climb the peak," identified by following density gradients, are labeled as its members. The valleys in between the peaks represent intersections between the clusters. These are used to define the boundaries of the clusters and also to form a parent–child relationship, thereby establishing a hierarchical organization of the groups. EnLink works by first calculating the densities of the data points using a set of qden nearest neighbors and then organizes the points in groups by using nearest neighbor links.
We present our results in the Appendix for both [Ca/Fe] and [r/Fe] for different values of γ over a wide dynamic range in the observed number of data points. We confirm that statistically significant groupings in abundance space can be recovered, particularly at low values of γ. For this work, we adopt a low cluster-mass limit of Mmin = 5 M☉ which is likely to be too conservative. For a fixed number of simulation particles, decreasing Mmin suppresses the number of detected groups.
5.2. Group Finding for Small n*
Clustering should be present even in the limit of only a few data points. To emphasize this fact, we have simulated the abundance measurements for a dwarf galaxy at a distance of 30 kpc (see Figures 7 and 8) as observed on 8 m class and 30 m class telescopes respectively. We adopt a stellar mass of 3 × 105 M☉ typical of a faint dwarf galaxy. This object has about 106 stars, a luminosity of 105L☉ and an absolute V mag of MV = −7.6 assuming a Salpeter IMF. The luminosity is a factor of two higher for a Kroupa IMF. The star counts are consistent with the model values in Table 1 when scaled to the adopted lower mass.
Figure 7. Simulation of a targeted study of a nearby dwarf galaxy on an 8 m (top) and 30 m (bottom) telescope. The data points are drawn from Figure 4 for a galaxy with a stellar mass of 3 × 105 M☉ at a distance of 30 kpc (see Table 1): (left) γ = 1.5 (right) no clustering. The simulated errors are 0.1 dex in the top figures and 0.05 dex in the bottom figures. There is evidence of clustering at [Fe/H] < −3.0 from a sample of 10 stars on an 8 m class telescope; the clustering is easily detected in the 30 m telescope experiment.
Download figure:
Standard image High-resolution imageFigure 8. Simulation of a targeted study of a nearby dwarf galaxy on an 8 m (top) and 30 m (bottom) telescope. The data points are drawn from Figure 4 for a galaxy with a stellar mass of 3 × 105 M☉ at a distance of 30 kpc (see Table 1): (left) γ = 2.0, (right) no clustering. The simulated errors are 0.1 dex in the top figures and 0.05 dex in the bottom figures. There is evidence of clustering at [Fe/H] < −3.0 from a sample of 10 stars on an 8 m class telescope; the clustering is easily detected in the 30 m telescope experiment.
Download figure:
Standard image High-resolution imageFor the 8 m experiment (Figure 7), we assume measurement errors of 0.1 dex in both [r/Fe] and [Fe/H]. For γ = 1.5 and γ = 2.0, the effects of clustering are evident and this holds true if we double the measurement error. The impact of this measurement uncertainty over the full simulation is shown in Figure 9. We conclude that, once more extensive studies are made of the nearest dwarf galaxies, the effects of clustering may become evident even before the advent of ELTs. We envisage projects which focus on relatively few stars that appear grouped in abundance space in low resolution spectroscopic data. Long integrations and differential analysis will allow the null hypothesis to be tested that the stars have identical abundances in all elements. For the 30 m experiment (Figure 8), we have assumed a general improvement in the atmospheric models and the experimental errors, and therefore adopt errors of 0.05 dex. The effects of clustering, which are easily seen, remain clearly visible even after a twofold increase in the measurement errors in both axes. This simulation is a powerful statement of the importance of multi-object echelles on ELTs.
Figure 9. Same models presented in Figure 4 but without the fourfold compression in the [r/Fe] axis. The top figures are for γ = 1.5 and γ = 2 and have an unrealistic intrinsic scatter of 0.01 dex. The bottom figures are repeated but with an intrinsic scatter of 0.1 dex. The effects of clumping are clearly seen in both distributions.
Download figure:
Standard image High-resolution imageFor a fixed qden and data dimensionality, the number of spurious groups due to Poisson noise increases linearly with the total number of data points n*. Therefore, EnLink can be used in the limit of small n* with qden set to 3, i.e., a minimum of one more than the number of data dimensions. But with so few data points, the full power of EnLink is not being exploited such that more rudimentary statistical techniques may be better. However, EnLink is particularly efficient in treating data sets with more than two dimensions, even in the limit of small n*. The significance of groups increases dramatically when we apply EnLink on an abundance space with more dimensions. The normalizing distribution in Equation (3) is easily extended to higher dimensions. In Figure 10, we apply EnLink to the 3D -space ([Fe/H], [Ca/Fe], [r/Fe]) for three different measurement errors (0.05, 0.1, 0.2 dex) typical of contemporary observations on 8 m telescopes at V = 18. Even in the presence of large errors, clustering signals are seen in all cases.
Figure 10. Results of EnLink group finding applied to the 3D space ([Fe/H], [Ca/Fe], [r/Fe]) for [Fe/H] < −3.0. The two rows show results for N = 100 and 300 data points. The two columns present results for γ = 1.5, 2.0. The histograms are defined in Figure 12. The simulated measurement errors are now 0.05 (red), 0.10 (blue), and 0.20 (purple) dex. The effects of clustering are apparent, even in the limit of small statistics and with larger measurement errors.
Download figure:
Standard image High-resolution image6. DISCUSSION
This paper has explored the prospect of probing the mass scales of the first star clusters. We stress that we have used a lower cluster-mass limit of Mmin = 5 M☉ (typically 10 stars) which is very conservative. A more reasonable value may be an order of magnitude higher (cf. Bland-Hawthorn et al. 2010). For γ = 2 and a fixed number of simulation particles, the lower threshold has the effect of reducing cluster membership by a factor of 10, and increasing the "background" by the same factor. This lowers the overall clustering signal by an order of magnitude. But we adopt the conservative lower mass limit in order to account for a possible dwarf stellar population that are not born in clusters. We were unable to find any observational constraints on the diffuse versus clustered population in dwarf galaxies (cf. Lada & Lada 2003).
In our conservative analysis, we find that there is an intimate connection between properties of the ICMF and the amount of potentially detectable clustering in the abundance plane. A flat ICMF and/or a ICMF with a high mass cutoff produces strong clustering in the [Fe/H] versus [X/Fe] abundance plane (-space). While our models are inevitably oversimplified, the phenomenon should be detectable on 8–10 m telescopes (e.g., Figures 7 and 8). This gains support from existing observations of open clusters, globular clusters and moving groups (Castro et al. 1999; Shen et al. 2005; Randich et al. 2006; Sestito et al. 2007; De Silva et al. 2009; Chou et al. 2010; Bubar & King 2010). A clean "clustering" signature in -space, particularly at low metallicity, is important for a number of reasons. First, it indicates the presence of massive star clusters in the early universe and conceivably provides a constraint on the mass of the first systems. Second, it provides a clean signal of the progenitor abundances in the cloud prior to cluster formation. This abundance measurement is averaged over a substantial amount of gas and is therefore not subject to mixing anomalies (Karlsson & Gustafsson 2001) or mass transfer in binaries (e.g., Suda et al. 2004; Ryan et al. 2005; Lucatello et al. 2005).
Strong clustering would indicate a highly flattened ICMF, or a high mass cutoff. This could herald the onset of the formation of massive star clusters in dwarf galaxies (e.g., Bromm & Clarke 2002). If the star formation efficiencies were low at that time, this may require supermassive gas clouds (≳107 M☉) to have formed even at the earliest times (Abel et al. 2000), possibly consistent with the regular occurrence of massive star-forming clumps at high redshift (Genzel et al. 2006; Förster-Schreiber et al. 2009; Elmegreen & Elmegreen 2006). Conversely, if such clustering was not observed, then we would infer that the slope of the early ICMF is steep, or the maximum cluster size is relatively small compared to the present day. But the observed scatter would need to be consistent with the non-detection of clustering.
In future investigations, from the perspective of chemical signatures, we will look at the degeneracy between steep ICMFs with a high mass cutoff and flatter ICMFs with a lower mass cutoff (see Section 4.2). We will also look at a wider class of chemical elements that are considered in numerical simulations of the first stars. We will look at the improvement in cluster identification with more chemical elements, particularly in the limit of small n*. The clustered abundance signatures will provide unique insight into the most ancient star clusters. These signatures are signposts of the chemistry immediately before the onset of star formation, untainted by mass transfer in close binary pairs or incomplete mixing anomalies.
Finally, it is an extraordinary fact that we can probe back to the first billion years from observations of the local universe. We can say with absolute certainty that stars existed at this time. These were responsible for the first chemical elements (Ryan-Weber et al. 2006) and for reionizing the fog of hydrogen that permeated the early Universe (Fan et al. 2002). Precisely when the first star clusters formed is unknown. It seems likely, however, that gas was able to fragment at very high density even at primordial abundance levels (Clark et al. 2008). It may be possible to directly probe these environments in an era of the Atacama Large Millimetre Array and the James Webb Space Telescope. But we believe that some of the most important insights, particularly with regard to progenitor yields, will undoubtedly come from near-field cosmology. To this end, it will be necessary to equip the next generation of ELTs with wide-field multi-object spectrographs that operate at high spectroscopic resolution (R ≳ 20,000).
J.B.H. is supported by an Federation Fellowship from the Australian Research Council (ARC), which also funds T.K.'s research position. S.S. is funded under the ARC DP grant 0988751 which partially supports the HERMES project. M.R.K. is supported by the National Science Foundation through grant AST-0807739; by NASA through the Spitzer Space Telescope Theoretical Research Program, provided by a contract issued by the Jet Propulsion Laboratory; and by the Alfred P. Sloan Foundation through a Sloan Research Fellowship. J.B.H. is indebted to Merton College, Oxford for a Visiting Research Fellowship, and to the Leverhulme Trust for a Visiting Professorship to Oxford. J.B.H. and T.K. are grateful to the BIPAC Institute, Oxford, for their hospitality.
APPENDIX: GROUP FINDING IN AN ABUNDANCE SPACE
In the EnLink clustering scheme, each group is characterized by a maximum density ρmax and a minimum density ρmin, and these are used to define its significance S as
where σln(ρ) is the standard deviation associated with the density estimator and is a constant for a given dimensionality and qden.
For Poisson-sampled data the distribution of density as estimated by the code using the kernel scheme is log-normal and the variance satisfies the relation
where qden is the number of neighbours employed for density estimation, the volume of a d-dimensional unit hypersphere and ||W||22 the L2 norm of the kernel function (Sharma & Johnston 2009). For qden = 6 and d = 2, σln(ρ) evaluates to 0.4714.
Thus EnLink has two free parameters: (1) the significance threshold of the group ST, and (2) the number of nearest neighbours qden used for density estimation. The variable qden should be set to less than the minimum desired size of the groups because the density is smoothed over a scale of qden nearest neighbours such that the significance and hence the probability of detecting groups of size less than qden is drastically reduced. Additionally, qlink = min(10, qden − 1) neighbours are used for linking the groups, which means groups whose density peaks lie within qlink nearest neighbours of each other cannot be separated. Since we are interested in identifying groups with less than 10 data points, we set qden = 6; the case for n* ≲ 6 is discussed in the next section.
Our initial analysis is for data points with [Fe/H] < −2.5. This includes a crowded, high-density region of the abundance plane which skews the clustering analysis considerably. However, this may be an important regime if the first chemical elements arise from pair instability SNe (Karlsson et al. 2008). The significance of spurious groups is distributed almost as a Gaussian distribution and hence the significance threshold ST is used to suppress these groups. An improved version of the empirical formula (Sharma & Johnston 2009) for the expected number of spurious groups, valid for ST>1, is given by
where is a small correction term and n* is the number of data points.9 In Figures 11 and 12, we plot the significance distribution S of identified groups for data sets with different values of n* and γ as labelled on the plots.
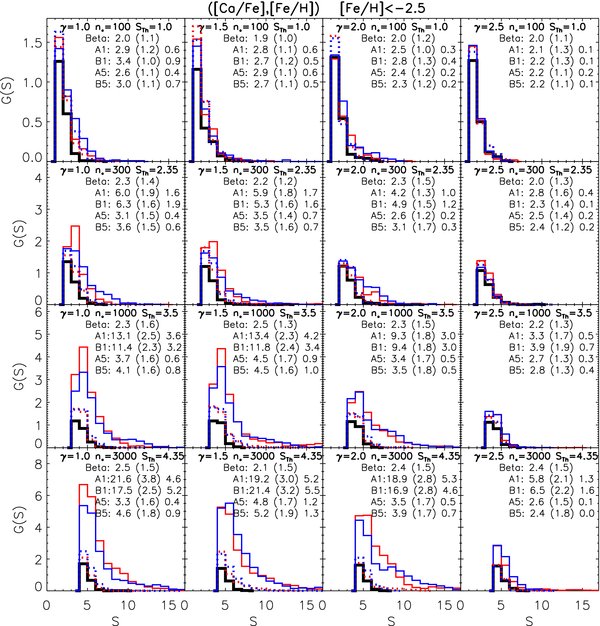
Figure 11. Results of EnLink group finding applied to the models presented in Figure 3 at a metallicity cutoff [Fe/H] < −2.5. The models represent the two-dimensional space ([Fe/H], [Ca/Fe]) where the four rows show results for n* = 100, 300, 1000, 3000 data points. The four columns present results for γ = 1.0, 1.5, 2.0, 2.5. In each panel, there are five distinct significance distribution functions G(S) (Equation (15)); note that the vertical range increases as n* increases (see Section 5.1). The black histogram is the EnLink analysis of the control sample generated by the beta distribution in equation 3 which, by definition, has no clustering. The solid blue and red histograms (A1, B1) are the analysis of the A and B realizations respectively (0.01 dex uncertainty) shown in Figure 3; the dotted histograms (A5, B5) repeat the analysis for an abundance uncertainty of 0.05 dex. The statistical means and uncertainties (in brackets) for all distributions are given in the insets; the third value is the CS statistic (see the text).
Download figure:
Standard image High-resolution imageFigure 12. Results of EnLink group finding applied to the models presented in Figure 4 at a metallicity cutoff [Fe/H] < −2.5. The models represent the two-dimensional space ([Fe/H], [r/Fe]) where the four rows show results for n* = 100, 300, 1000, 3000 data points. The four columns present results for γ = 1.0, 1.5, 2.0, 2.5. In each panel, there are five distinct significance distribution functions G(S) (Equation (15)); note that the vertical range increases as n* increases (see Section 5.1). The black histogram is the EnLink analysis of the control sample generated by the beta distribution in Equation (3) which, by definition, has no clustering. The solid blue and red histograms (A1, B1) are the analysis of the A and B realizations respectively (0.01 dex uncertainty) shown in Figure 4; the dotted histograms (A5, B5) repeat the analysis for an abundance uncertainty of 0.05 dex. The statistical means and uncertainties (in brackets) for all distributions are given in the insets; the third value is the CS statistic (see the text).
Download figure:
Standard image High-resolution imageWe set ST such that the expected number of spurious groups (false positives) with S>ST is about 2 in all data sets which we calibrate from the beta models. ST is set to 1.0, 2.35, 3.5 and 4.35 for data with n* as 100, 300, 1000 and 3000 respectively. This number is increasing because, for a fixed qden and data dimensionality, the number of spurious groups due to Poisson noise increases linearly with the total number of data points n*.
Each panel shows the outcome of five EnLink analyses: the cluster-less beta model (solid black line); the simulated models A1 and B1 having unrealistic abundance errors 0.01 dex shown as solid red and blue curves respectively; the simulated models A5 and B5 having abundance errors 0.05 dex shown as dotted red and blue lines respectively. In each panel, the mean number of identified groups G along with its dispersion σG is also given. The mean and dispersion were calculated using 100 random realizations of each data type. The plotted distributions are also averaged over these 100 random realizations. We also provide a measure of the statistical significance of detecting clusters in a data set as follows. If GB is the number of groups as predicted by the smooth beta model, the statistical significance of clustering in a model is given by
The third column shows the value of CS for each data set.
It can be seen in Figure 11 and 12 that the expected number of spurious groups for the beta models are nearly independent of the value of γ, which is a consequence of the adaptive metric scheme. Specifically, EnLink uses the concept of a locally adaptive metric, which is used for calculating densities and nearest neighbours of data points (a refinement over earlier developments by Ascasibar & Binney 2005) to increase the efficiency of detecting clusters in multi-dimensional spaces. If instead clustering is performed using a Euclidean metric on raw data, the significance distribution of spurious groups due to Poisson noise is found to vary with the distribution of points in the abundance space, e.g., the beta models with different values of γ.
In the limit of few data points, the locally adaptive metric scheme is equivalent to using a metric which is given by the inverse of the dispersion along each dimension. As a check we also performed the analysis using this simpler scheme and found equivalent results, thereby demonstrating the robustness of our group-finding analysis. For the sake of accuracy, we use the beta models to evaluate the significance of clustering, but strictly speaking this is not required and any Poisson sampled cluster-less data would also suffice. In fact, the empirically derived formula given by Equation (A3) can also be used directly to predict the number of spurious groups.
Next we compare the parameter CS for the different cases. It can be seen that as n* and γ increase, CS increases also. First we look at cases with unrealistic measurement errors of 0.01 dex. It is clear that the γ = 2.5 models are nearly undetectable for all values of n* and closely resemble the beta models. For γ = 2.0, a minimum value of n* = 300 is needed for CS ≳ 1. For lower values of γ, signatures of clustering are visible with as few as 100 points. Increasing the abundance errors to 0.05 dex significantly affects our ability to detect clusters. When sufficient number of data points are present, the A5 and B5 models perform better for γ = 1.5 and 2.0 as compared to γ = 1. This is because the clusters in these cases are more in number, are spread over a larger area, are less crowded, and hence easier to detect.
Since clustering is most prominent for lower values of [Fe/H], we also investigated data sets with a lower metallicity cutoff, [Fe/H] < −3.0. These results are shown in Figures 13 and 14. The parameter CS is found to increase in general for all cases, unlike what is seen in the [Fe/H] < −2.5 analysis (Figures 11 and 12). It is striking how much better EnLink performs on these simulations which is to be expected given the broader intrinsic dispersions of [r/Fe] in the models. In light of these results, another way to look at Figure 4 is the significance S of clustering over the abundance plane. In Figure 15, we show the S contours for the four different values of γ with lower significance regions to high [Fe/H]. Clustered abundance data points near the mean value of [r/Fe] are more likely at low [Fe/H] for low values of γ. Clustered abundance data points away from the mean are favoured by higher values of γ.
Figure 13. Results of EnLink group finding applied to the models presented in Figure 3 for [Fe/H] < −3.0. The two rows show results for n* = 100 and 300 data points. The four columns present results for γ = 1.0, 1.5, 2.0, 2.5. The histograms are defined in Figure 11. The effects of clustering are now more apparent, even in the limit of small statistics.
Download figure:
Standard image High-resolution imageFigure 14. Results of EnLink group finding applied to the models presented in Figure 4 for [Fe/H]<−3.0. The two rows show results for n* = 100 and 300 data points. The four columns present results for γ = 1.0, 1.5, 2.0, 2.5. The histograms are defined in Figure 12. The effects of clustering are now more apparent, even in the limit of small statistics.
Download figure:
Standard image High-resolution imageFigure 15. Statistical significance distribution S (Equation (13)) for the four clustered models presented in Figure 4. The contours are (from right to left): S = 2, 4, 6, 8, 10, 12. Note, for example, groupings of data points are more likely near the mean value of [r/Fe] at low [Fe/H] for low γ. Clustered abundance data points away from the mean are favored by higher values of γ.
Download figure:
Standard image High-resolution imageFootnotes
- 6
Homogeneity could also fail in very massive clusters, those larger than ∼107 M☉ (Maraston et al. 2004; Larsen 2009). However, in this case even if the whole clusters were not chemically homogeneous, smaller mass portions within them would be, and there is little distinction from the standpoint of the model we present below. The effect would simply be to break up very large clusters into a number of chemically homogeneous small clusters. Given that large clusters are rare, this would not affect our signal significantly.
- 7
In the standard notation, for a given star with a measured abundance ratio (X/Fe)*, it is convenient to write [X/Fe] = log10(X/Fe)* − log10(X/Fe)☉ which is a logarithmic scale normalized to solar abundances.
- 8
Note that in the abundance plane, .
- 9
Since the distribution in S for spurious groups is roughly normal (Equation (15)), S can be loosely interpreted as the statistical z-score for finding a group per unit data point.
















![$\log {d} f_* / {d\rm [Fe/H]} = 1$](https://content.cld.iop.org/journals/0004-637X/721/1/582/revision1/apj351161ieqn10.gif)
![$\rm [Fe/H] \approx -1.5$](https://content.cld.iop.org/journals/0004-637X/721/1/582/revision1/apj351161ieqn11.gif)





































![$\sigma ({\rm [Fe/H]}) \propto 10^{-0.5\rm [Fe/H]}$](https://content.cld.iop.org/journals/0004-637X/721/1/582/revision1/apj351161ieqn8.gif)