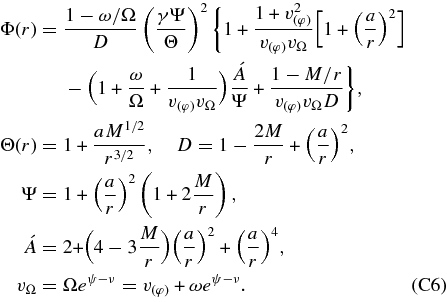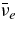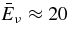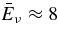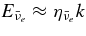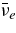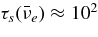ABSTRACT
The standard massive accretion disk with Keplerian angular momentum (standard accretion disk) producing gamma-ray bursts (GRBs) is investigated on the bases of the microphysics of neutrinos and general relativity. Since the accretion disk gradually heated by viscosity is efficiently cooled by antielectron neutrinos, 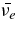 , the accreting flow maintains a relatively low temperature, T ≈ 3 × 1010 K, over a long range of accreting radius that produces very high dense matter around a rotating black hole, ρ ⩾ 1013 g cm−3. Thus, the massively accreting matter is in the domain of heavy nuclei all over the accreting flow onto a central black hole where the fraction of evaporated free neutrons is large, Yn ≈ 0.8, and that of protons is infinitesimal, Yp ≈ 10−4. The electron neutrinos in the disk are almost absorbed by rich neutrons while the antielectron neutrinos are little absorbed by rarefied protons. The mean energy of antielectron neutrinos ejected from the disk is extraordinarily high,
, the accreting flow maintains a relatively low temperature, T ≈ 3 × 1010 K, over a long range of accreting radius that produces very high dense matter around a rotating black hole, ρ ⩾ 1013 g cm−3. Thus, the massively accreting matter is in the domain of heavy nuclei all over the accreting flow onto a central black hole where the fraction of evaporated free neutrons is large, Yn ≈ 0.8, and that of protons is infinitesimal, Yp ≈ 10−4. The electron neutrinos in the disk are almost absorbed by rich neutrons while the antielectron neutrinos are little absorbed by rarefied protons. The mean energy of antielectron neutrinos ejected from the disk is extraordinarily high, 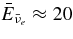 MeV, because the antielectron neutrinos are degenerated in the high dense disk. The huge antielectron neutrinos with high mean energy and large luminosity,
MeV, because the antielectron neutrinos are degenerated in the high dense disk. The huge antielectron neutrinos with high mean energy and large luminosity, 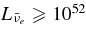 erg s−1, are ejected from the massive accretion disk. The antielectron neutrinos are possibly the sources of the relativistic jets producing GRBs.
erg s−1, are ejected from the massive accretion disk. The antielectron neutrinos are possibly the sources of the relativistic jets producing GRBs.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
In the widely believed model of gamma-ray bursts (GRBs), the high-energy emission arises in the relativistic jets ejected from a central engine (Piran 2005). The formation of a relativistic jet has been investigated in two ways. The first way is owing to magnetic field. The rotating magnetized compact objects with matter accretion can generate strong toroidal magnetic fields driving highly magnetized plasmas into relativistic jets (Blandford & Znajek 1977; Balbus & Hawley 1998; Proga et al. 2003; Shibata et al. 2008; McKinney & Blandford 2009; Komissarov et al. 2009). Though of significant concern is that a strong toroidal field in the jets is unstable to the non-axisymmetric helical kink mode leading to rapid disruption (Bateman 1978), McKinney & Blandford (2009) had found that the supply of baryonic matter into a jet stabilizes the magnetohydrodynamical jet and constructs a long jet with a narrow angle. It is a subject in the origin of a relativistic jet by magnetic field that the energy density in front of an expanding jet can be produced superior to the rest-mass density.
The other formation mechanism of a jet is owing to neutrinos. The 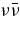 -annihilation near accreting black holes can raise the energy deposition in the close vicinity of the black holes by the reactions
-annihilation near accreting black holes can raise the energy deposition in the close vicinity of the black holes by the reactions 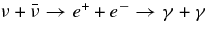 . The resulting e+e−-pair plasma–photon fireball can power a relativistic outflow of baryons (Cooperstein et al. 1986; Goodman et al. 1987; Jaroszynski 1993, 1996; Ruffert & Janka 1999; Salmonson & Wilson 1999; Asano & Fukuyama 2000; Madau & Thompson 2000; Miller et al. 2003; Belorborodov 2003; Birkl et al. 2007). However, it has been shown in the model of GRBs that most of the neutrinos are trapped in accreting matter falling into a black hole (Di Matteo et al. 2002; Chen & Belobororodov 2007; Kawanaka & Mineshige 2007). Nevertheless, it should be recognized first that the interaction of heavy nuclei with ambient free nucleons, which has been ignored in previous works, produces rich free neutrons and rare free protons in high dense matter. Second, the simplified assumption in previous works, the detailed balance in neutrino reactions, restricts the variations of thermodynamic quantities, ρ and T, and makes a particular thermal history of accreting matter. The rapidly transient matter in the massive accretion hardly satisfies the detailed balance. Third, the previous models of the massive accretion are based on the advection dominant flow (ADAF) and then the heating or cooling by advection is efficient while that is inefficient in standard accretion disk (STAD). The strong compression by the rapid deceleration of the flow at the middle region of the accretion disk largely heats up the accreting matter to be in the state of free nucleons. The gradual heating in STAD maintains the accreting matter in the domain of heavy nuclei. These different aspects in the massive accretion from previous works will produce the new thermal history of accreting matter and drive the neutrino ejection from the disk as a source of relativistic jets.
. The resulting e+e−-pair plasma–photon fireball can power a relativistic outflow of baryons (Cooperstein et al. 1986; Goodman et al. 1987; Jaroszynski 1993, 1996; Ruffert & Janka 1999; Salmonson & Wilson 1999; Asano & Fukuyama 2000; Madau & Thompson 2000; Miller et al. 2003; Belorborodov 2003; Birkl et al. 2007). However, it has been shown in the model of GRBs that most of the neutrinos are trapped in accreting matter falling into a black hole (Di Matteo et al. 2002; Chen & Belobororodov 2007; Kawanaka & Mineshige 2007). Nevertheless, it should be recognized first that the interaction of heavy nuclei with ambient free nucleons, which has been ignored in previous works, produces rich free neutrons and rare free protons in high dense matter. Second, the simplified assumption in previous works, the detailed balance in neutrino reactions, restricts the variations of thermodynamic quantities, ρ and T, and makes a particular thermal history of accreting matter. The rapidly transient matter in the massive accretion hardly satisfies the detailed balance. Third, the previous models of the massive accretion are based on the advection dominant flow (ADAF) and then the heating or cooling by advection is efficient while that is inefficient in standard accretion disk (STAD). The strong compression by the rapid deceleration of the flow at the middle region of the accretion disk largely heats up the accreting matter to be in the state of free nucleons. The gradual heating in STAD maintains the accreting matter in the domain of heavy nuclei. These different aspects in the massive accretion from previous works will produce the new thermal history of accreting matter and drive the neutrino ejection from the disk as a source of relativistic jets.
The massive accretion disk with the reactions of neutrinos has been studied in a number of works (Popham et al. 1999; Narayan et al. 2001; Kohri & Mineshige 2002; Kohri et al. 2005; Di Matteo et al. 2002; Lee et al. 2005; Chen & Belobororodov 2007; Kawanaka & Mineshige 2007). These models of accretion are based on the ADAF. At the outer region, r ⩾ 102rg, the main composition of the matter is the heavy nucleus and the fraction of free nucleons is small where the viscously heated fluid is cooled mainly by the rapid advection. At the middle region, 10rg < r < 102rg, the accreting fluid is in turn heated mainly by the rapid compression. However, the magnetohydrodynamics of the accreting flow with self-consistent viscosity cannot behave like drastic radial motion (De Villiers & Hawley 2003; De Villiers et al. 2003, 2005; Hirose et al. 2004; Krolik et al. 2005), and then the significant cooling or heating by advection does not seem to be expected.
We consider here the massive accretion disk with Keplerian angular momentum, i.e., a STAD model proposed by Shakura & Sunyaev (1973) and Novikov & Thorne (1973) where the accretion disk is efficiently cooled by photons or neutrinos. The formation of collimated jets requires pre-collapsed matter of a massive star with sufficient angular momentum (Woosley & Janka 2005). The initial pre-collapsed matter with the freely falling time  being less than the duration of γ-ray emission, tγ ≈ 10 s, has the density ρ ⩾ G/t2γ ≈ 105 g cm−3. When the pre-collapsed matter with density ρ = 105 g cm−3 has the angular momentum J ⩾ 10−1JK, at the radius r = 109 cm, the accretion disk with Keplerian angular momentum may be formed at the radius r ⩾ 107 cm, where JK is the Keplerian angular momentum. The thermal history of accreting matter in ADAF is dissimilar to that in STAD. As a result, the neutrinos generated in ADAF are almost absorbed by rich nucleons heated by advection. The STAD holds the heat balance between the non-violent heating by viscosity and the neutrino cooling, and then maintains the temperature to be relatively cold over the wide radial range of the flow. The proton-poor disk with high density ejects huge antielectron neutrinos. It is shown here that the antielectron neutrino is a candidate for the source of relativistic jets.
being less than the duration of γ-ray emission, tγ ≈ 10 s, has the density ρ ⩾ G/t2γ ≈ 105 g cm−3. When the pre-collapsed matter with density ρ = 105 g cm−3 has the angular momentum J ⩾ 10−1JK, at the radius r = 109 cm, the accretion disk with Keplerian angular momentum may be formed at the radius r ⩾ 107 cm, where JK is the Keplerian angular momentum. The thermal history of accreting matter in ADAF is dissimilar to that in STAD. As a result, the neutrinos generated in ADAF are almost absorbed by rich nucleons heated by advection. The STAD holds the heat balance between the non-violent heating by viscosity and the neutrino cooling, and then maintains the temperature to be relatively cold over the wide radial range of the flow. The proton-poor disk with high density ejects huge antielectron neutrinos. It is shown here that the antielectron neutrino is a candidate for the source of relativistic jets.
In the previous works of ADAF, the free nucleons have been treated to be independent of heavy nuclei even in the dominant component of heavy nuclei, Xf < 0.5, where Xf is the mass fraction of the free nucleon Xf(ρ, T) (Qian & Woosley 1996; Meyer 1994). We investigate here the neutrino reactions to the evaporated free nucleons interacting with heavy nuclei, where the chemical potentials of neutrons and protons, μn and μp, are equal in the two phases of evaporated free nucleon gas and the condensed heavy nucleus (Lamb et al. 1981; Lattimer & Swesty 1991). It is shown that the accretion disk at all the locations in the region rin ≈ rg < r ⩽ 102rg, is cooled mainly by antielectron neutrinos, where rin is the inner boundary radius of the viscously heating disk. The massively accreting matter in STAD is in the domain of heavy nuclei all over the flow accreting onto a black hole. Therefore, the emitting rates of neutrinos should be precisely expressed in the existence of heavy nuclei.
The reactions of leptons in the previous works of ADAF have been assumed to hold the detailed balances (Belorborodov 2003). In the neutrino-transparent matter, the rates of e− and e+ captures by nucleons have been set to be equal, 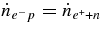 . In the neutrino-opaque matter, the detailed balances have been now assumed to hold e− + p ↔ n + νe and
. In the neutrino-opaque matter, the detailed balances have been now assumed to hold e− + p ↔ n + νe and 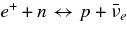 . These conditions of the detailed balance restrict the variations of ρ, T, and Ye along the flow. As is presented here, these simplified assumptions of detailed balance are not adequate for the massive accretion with degenerated electrons. Though the reactions of electrons have been treated in the approximation of small degeneracy, ηe = μe/kT < 1 (Belorborodov 2003), we treat it in arbitrary degeneracy ηe since the electrons are degenerated in the massive accretion, ηe>4. We solve the lepton reactions by direct methods without equilibrium conditions.
. These conditions of the detailed balance restrict the variations of ρ, T, and Ye along the flow. As is presented here, these simplified assumptions of detailed balance are not adequate for the massive accretion with degenerated electrons. Though the reactions of electrons have been treated in the approximation of small degeneracy, ηe = μe/kT < 1 (Belorborodov 2003), we treat it in arbitrary degeneracy ηe since the electrons are degenerated in the massive accretion, ηe>4. We solve the lepton reactions by direct methods without equilibrium conditions.
The large amount of energy deposition by neutrinos could produce a relativistic jet. Qian & Woosley (1996) and Herant et al. (1994) had developed the explosion mechanism of a supernova driven by the neutrino heating. Qian & Woosley (1996) had shown that the mass outflow, "neutrino-driven wind," is produced when the sufficient flux of neutrinos, Lν ⩾ 1052 erg s−1, with high mean energy,  20 MeV, supplied from a newly born neutron star. If the number density of
20 MeV, supplied from a newly born neutron star. If the number density of  is sufficiently large in the massive accretion disk, the degeneracy of
is sufficiently large in the massive accretion disk, the degeneracy of 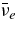 ,
, 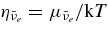 , becomes large. The antielectron neutrinos with the high mean energy of
, becomes large. The antielectron neutrinos with the high mean energy of 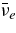 in comparison with the thermal energy of accreting matter,
in comparison with the thermal energy of accreting matter,  , will be ejected from the accretion disk. When the outflow produced by
, will be ejected from the accretion disk. When the outflow produced by 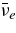 becomes a one-dimensional flow along the rotational axis of the disk, the required luminosity and mean energy of neutrinos may be Lν < 1052 erg s−1 and
becomes a one-dimensional flow along the rotational axis of the disk, the required luminosity and mean energy of neutrinos may be Lν < 1052 erg s−1 and 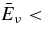 20 MeV, since the decreasing rate of entropy density in the one-dimensional flow is less in comparison with that of the radial flow. The one-dimensional outflow driven by neutrinos may form a narrow beam since the rapid expansion of the flow due to the neutrinos acceleration enforces the larger reduction of pressure of the flow than that of the surrounding matter (Yokosawa 1982). We investigate here the luminosity, Lν, and the mean energy,
20 MeV, since the decreasing rate of entropy density in the one-dimensional flow is less in comparison with that of the radial flow. The one-dimensional outflow driven by neutrinos may form a narrow beam since the rapid expansion of the flow due to the neutrinos acceleration enforces the larger reduction of pressure of the flow than that of the surrounding matter (Yokosawa 1982). We investigate here the luminosity, Lν, and the mean energy, 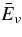 , of neutrinos ejected from a massive accretion disk.
, of neutrinos ejected from a massive accretion disk.
The paper is organized as follows. In Section 2, the microphysics of neutrinos is described. The emissivity and the particle flux of each flavor of neutrinos are calculated on the basis of the stationary structure of the massive accretion disk. In Section 3, the relativistic model of an accretion disk is presented. The density and temperature are determined in the heat balance between the viscous heating and the neutrino cooling. In Section 4, the results of the massive accretion disk are shown. The effects of heavy nuclei on the chemical potentials of free nucleons are represented in Section 4.1. The degeneracy of accreting particles is depicted in Section 4.2. The profiles of the composition of accreting matter are given in Section 4.3. The structures of the disk are shown in Section 4.4. The emissivities and opacities of neutrinos are presented in Section 4.5. In Section 4.6, the luminosity and mean energy of neutrinos are given over a wide range of the mass scale and of the angular momentum of a black hole. In Section 5, we discuss the thermal instability of the accretion disk. We summarize the new results in this paper in comparison with previous works in Section 6. In Appendix A, the cross sections of neutrinos, opacities, emissivities, and the reaction rates of neutrinos are summarized. The neutrino transfer in a homogeneous disk and the dynamics of the rotating fluid in Kerr spacetime are presented in Appendices B and C.
2. MICROPHYSICS OF ACCRETING MATTER
The massive accretion disk producing GRBs has the state of matter with ρ = 109 ∼ 1014 g cm−3 and T = 1010 ∼ 1011 K which is the same state in the iron core collapse forming a neutron star (Bruenn 1985). The nuclear statistical equilibrium abundance of nuclei is nonzero in this state (Meyer 1993, 1994). Lattimer et al. (1985) have derived the thermally equilibrium state of the mixture; nuclei, nucleons, α-particles, electrons, and photons, where the nuclei are assumed to consist of a Wigner–Seitz cell with central nuclei surrounded by a nucleon vapor containing also α-particles. Because of the attractive nuclear forces, the nuclear component condenses into nuclei. Outside of these, we have a low-density "gas" of nucleons and α-particles. Thus, we have a two-phase system; the chemical potential μ must be continuous at the boundary between the two phases, both for neutrons and protons. Lattimer & Swesty (1991) have presented the chemical potential difference, 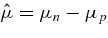 , as a function of the inputs (ρ, T, Ye). The number ratio of protons to neutrons in the vapor gas phase is expressed by
, as a function of the inputs (ρ, T, Ye). The number ratio of protons to neutrons in the vapor gas phase is expressed by

The leptons, e−, e+, and νi, react mainly to protons and neutrons in the vapor gas phase.
The rate of e− capture on protons can be derived from the standard electroweak theory (Tubbs & Schramm 1975; Yueh & Buchler 1976; Bruenn 1985; Burrows 2001):
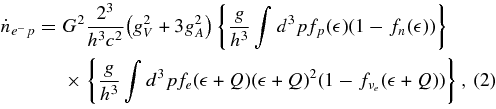
where the factor G2 is the Fermi constant with the value G2 = 5.18 × 10−44 MeV2 cm2, gV and gA are the constants, gV = 1 and gA = 1.23, g is the spin degeneracy, fi( ) is the Fermi–Dirac occupation function of an i-particle, fi(
) is the Fermi–Dirac occupation function of an i-particle, fi( ) = [1 + exp((
) = [1 + exp(( − μi)/kT)]−1, and Q is Q = (mn − mp)c2. The number density of the i-Fermi particle is given by
− μi)/kT)]−1, and Q is Q = (mn − mp)c2. The number density of the i-Fermi particle is given by
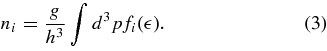
The energy of an i-particle,  , is related to its rest mass, mi, and momentum, p, as
, is related to its rest mass, mi, and momentum, p, as  2 = m2ic4 + p2c2. The former part of the integral of the distribution function in the above expression (Equation (2)) is rewritten as
2 = m2ic4 + p2c2. The former part of the integral of the distribution function in the above expression (Equation (2)) is rewritten as

The quantity ηpn is the dynamic structure factor for the electron–proton interaction and is equal to np in the nondegenerate regime of a proton. The capture rate of e+ on neutrons is similarly expressed by
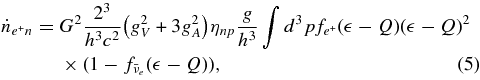
where the quantity ηnp is

The difference of chemical potential 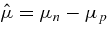 is positive because all the nuclei concerned have an excess of neutrons. In the high dense and hot matter of the collapse of iron core, the difference is generally large,
is positive because all the nuclei concerned have an excess of neutrons. In the high dense and hot matter of the collapse of iron core, the difference is generally large, 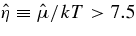 (Bethe 1990). The fraction of protons in the gas phase becomes
(Bethe 1990). The fraction of protons in the gas phase becomes 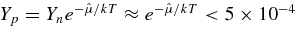 . The creation rate of electron neutrinos νe by the reaction e + p → νe + p is slow, and the absorption rate of
. The creation rate of electron neutrinos νe by the reaction e + p → νe + p is slow, and the absorption rate of  by
by 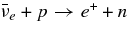 becomes little in the high dense and hot matter of the core collapse. When the core is slowly collapsed owing to the centrifugal force, the existence of nuclei is important for the reaction of neutrinos.
becomes little in the high dense and hot matter of the core collapse. When the core is slowly collapsed owing to the centrifugal force, the existence of nuclei is important for the reaction of neutrinos.
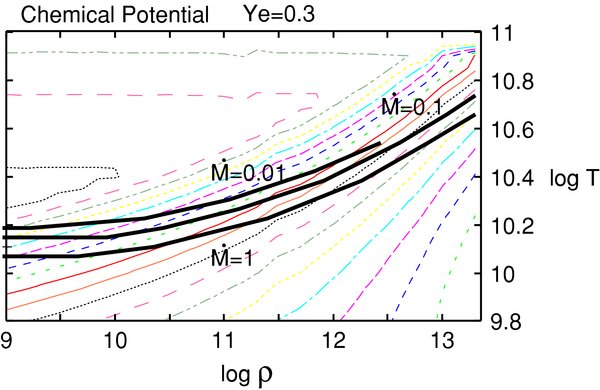
We adopt a simplified, analytical equation of state (EOS) for hot, dense matter given by Lattimer & Swesty (1991), in which the relevant thermodynamic quantities, i.e., nn, np, nα, μn − μp, A, Z, Pb, are represented as a function of the inputs (ρ, T, Ye), where nn, np, nα are the number densities of the free neutron, free proton, and α-particle, μn − μp is the difference of chemical potentials between the free neutron and proton, A and Z are the mean mass number and proton number of heavy nuclei. We have constructed a three-dimensional table of these thermodynamic quantities as a function of the inputs (ρ, T, Ye). One of the contour maps of the differential chemical potential, μn − μp, for Ye = 0.3, is represented in Figure 1.
Figure 1. Loci of the accreting matter with the accretion rate, 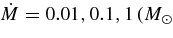 s−1), on the ρ(g cm−3)–T(K) plane. The contours of the difference in chemical potential between free neutrons and protons, μn − μp, of the hot and dense matter with a typical electron fraction, Ye = 0.3, are overplotted. The contours of constant potential, μn − μp, of the gaseous free nucleons without heavy nuclei are almost horizontal, which locate in the high-temperature region. The profile of the contours changes remarkably at the phase boundary between the gaseous free nucleons and the matter with heavy nuclei, where μn,G − μp,G = μn,A − μp,A; the left-hand side of the equation is the potential difference of gaseous free nucleons without heavy nuclei and the right one is that with heavy nuclei. At the domain above the phase boundary, the matter consists of free neutrons, protons, and α-particles.
s−1), on the ρ(g cm−3)–T(K) plane. The contours of the difference in chemical potential between free neutrons and protons, μn − μp, of the hot and dense matter with a typical electron fraction, Ye = 0.3, are overplotted. The contours of constant potential, μn − μp, of the gaseous free nucleons without heavy nuclei are almost horizontal, which locate in the high-temperature region. The profile of the contours changes remarkably at the phase boundary between the gaseous free nucleons and the matter with heavy nuclei, where μn,G − μp,G = μn,A − μp,A; the left-hand side of the equation is the potential difference of gaseous free nucleons without heavy nuclei and the right one is that with heavy nuclei. At the domain above the phase boundary, the matter consists of free neutrons, protons, and α-particles.
Download figure:
Standard image High-resolution imageThe dominant reactions of neutrinos in the massive accretion are presented in Table 1. The cross sections of these neutrino reactions have been studied by Tubbs & Schramm (1975), Bruenn (1985), and Burrows (2001), which are listed in Table 2 (Appendix A). The main reactions of leptons are the electron and positron captures on nucleons:
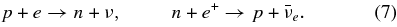
When the huge electron and positron pairs exist, n± ⩾ ne, the detailed equilibrium of e− and e+ capture on nucleons may be established:

Then, four chemical potentials hold the equilibrium condition:
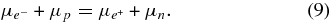
In the previous works of neutrino reactions, the detailed balance (Equation (8)) is assumed in the neutrino-transparent matter and the detailed balances, e− + p ↔ n + νe and 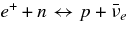 , are assumed in the neutrino-transparent matter (Belorborodov 2003). However, in the high dense matter with degenerated electrons, the pair creation of e− and e+ in the electromagnetic thermal bath is suppressed by the charge neutrality, which produces the condition n± ≪ ne. Thus, it is difficult for insignificant positrons to establish the detailed balances of e− and e+ captures on nucleons.
, are assumed in the neutrino-transparent matter (Belorborodov 2003). However, in the high dense matter with degenerated electrons, the pair creation of e− and e+ in the electromagnetic thermal bath is suppressed by the charge neutrality, which produces the condition n± ≪ ne. Thus, it is difficult for insignificant positrons to establish the detailed balances of e− and e+ captures on nucleons.
Table 1. Neutrino Reactions
| No. | Reaction Type | Reaction Process | References |
|---|---|---|---|
| 1 | e + p ⇌ νe + n | β-process | Burrows (2001) |
| 2 |  |
Positron capture on neutron | Burrows (2001) |
| 3 | e + A ⇌ νe + A' | Electron capture on nuclei | Bruenn (1985) |
| 4 | νi + N → νi + N | Neutrino–nucleon scattering | Burrows (2001) |
| 5 | νi + A → νi + A | Neutrino–nucleus scattering | Bruenn (1985) |
| 6 | νi + e → νi + e | Neutrino–electron scattering | Burrows (2001) |
| 7 | 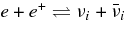 |
Electron pair process | Burrows (2001) |
| 8 | 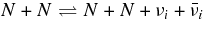 |
Nucleon–nucleon bremsstrahlung | Raffelt (2001) |
| 9 | n + n → n + p + e + νe | URCA process | Shapiro & Teukolsky (1983) |
| 10 |  |
Plasma decay | Ruffert et al. (1996) |
Download table as: ASCIITypeset image
Table 2. Cross Section
| No. | Neutrino Reaction | Cross Section |
|---|---|---|
| 1 | νe + n → e + p | ![$\sigma _{\nu _e, n}^a(\varepsilon _{\nu _e}) = \sigma _0\big(1+3g_A^2\big) \big(\frac{\varepsilon _{\nu _e}+Q}{2m_e c^2}\big)^2\big[1- \big (\frac{m_e c^2}{\varepsilon _{\nu _e}+Q}\big)^2\big]^{1/2}W_M$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn30.gif) |
| 2 | 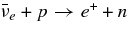 |
![$\sigma _{\bar{\nu }_e, p}^a(\varepsilon _{\bar{\nu }_e}) = \sigma _0\big(1+3g_A^2\big) \big (\frac{\varepsilon _{\bar{\nu }_e}-Q}{2m_e c^2} \big)^2 \big[1-\big (\frac{m_e c^2}{\varepsilon _{\bar{\nu }_e}-Q}\big)^2 \big]^{1/2} W_{\bar{M}}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn32.gif) |
| 3 | νi + p → νi + p | ![$\sigma _{p}^s(\varepsilon _{\nu _i}) = \sigma _0 \big (\frac{\varepsilon _{\nu _i}}{2m_e c^2}\big)^2 \big[4\sin ^4\theta _W-2\sin ^2\theta _W+ \frac{1+3g_A^2)}{4}\big]$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn33.gif) |
| 4 | νi + n → νi + n | 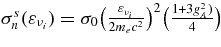 |
| 5 | νi + e → νi + e | ![$\sigma _e = \sigma _0\frac{1}{8}\big [(C_V+C_A)^2 + \frac{1}{3}(C_V-C_A)^2\big] \big(\frac{\varepsilon _{\nu _i}}{m_ec^2}+\frac{1}{2} \big)$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn35.gif) |
Notes. These cross sections are given by Burrows (2001). A convenient reference neutrino cross section is 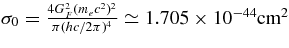 . The term, gA, is the axial-vector coupling constant (∼−1.26), θW is the Weinberg angle, and sin2θW ≃ 0.23, Q = mnc2 − mpc2 = 1.29332 MeV, and for a collision in which the electron gets all of the kinetic energy,
. The term, gA, is the axial-vector coupling constant (∼−1.26), θW is the Weinberg angle, and sin2θW ≃ 0.23, Q = mnc2 − mpc2 = 1.29332 MeV, and for a collision in which the electron gets all of the kinetic energy, 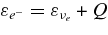 . WM is the weak magnetism/recoil correction and is approximately equal to (
. WM is the weak magnetism/recoil correction and is approximately equal to ( ). CV = 1/2 + 2sin2θW for νe and
). CV = 1/2 + 2sin2θW for νe and  , CV = −1/2 + 2sin2θW for νx and
, CV = −1/2 + 2sin2θW for νx and 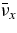 , CA = +1/2 for
, CA = +1/2 for 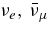 , and
, and 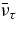 , and CA = −1/2 for
, and CA = −1/2 for 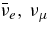 , and ντ.
, and ντ.
Download table as: ASCIITypeset image
We shall evaluate the above detailed balances in the massive accretion. The number density of a pair of e− and e+ in equilibrium with thermal photons is generally expressed as
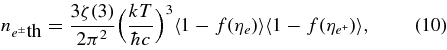
where the brackets indicate the mean values of the blocking factors in phase space and ζ(3) is the ζ function, ζ(3) = 1.202. The mean blocking is approximately represented with the mean energy of e− and e+, 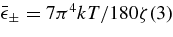 . Since the mean degenerate factor of electrons is taken in our massive accretion as
. Since the mean degenerate factor of electrons is taken in our massive accretion as 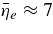 , the blocking factors are
, the blocking factors are
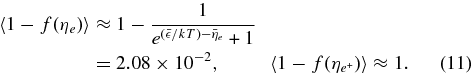
The number ratio of the pair to mean electron is
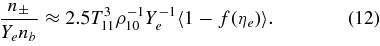
For the typical case of massive accretion, T = 3 × 1010 K, ρ = 1012 g cm−3, and Ye = 0.1, the pair of e− and e+ is infinitesimal:

The ratio of the capture rates, 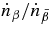 , is simply expressed by Equation (2)/Equation (5), and is evaluated by the typical quantities of the massive accretion in STAD, Yp ≈ 10−4, Ye ≈ 10−1, Yn ≈ 0.8, and
, is simply expressed by Equation (2)/Equation (5), and is evaluated by the typical quantities of the massive accretion in STAD, Yp ≈ 10−4, Ye ≈ 10−1, Yn ≈ 0.8, and 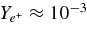 , as
, as
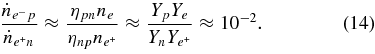
The reaction rate 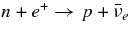 is extremely frequent in comparison with p + e− → n + νe.
is extremely frequent in comparison with p + e− → n + νe.
In the neutrino-opaque matter, the detailed balance, νe + n ⇌ e− + p, is also evaluated as follows. The difference in the reaction rate of the β-process is expressed as

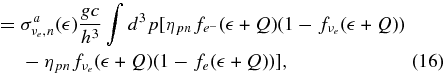
where 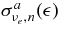 is the cross section of νe to n, νe + n → e− + p (Burrows 2001),
is the cross section of νe to n, νe + n → e− + p (Burrows 2001),
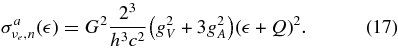
The ratio of the reaction rates is
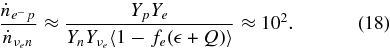
In the neutrino-opaque case of the typical massive accretion, the detailed balances, νe + n ⇌ e− + p, are not established.
Thus, the changing rate of each lepton number in unit volume, 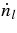 , is directly determined through the following networks of reactions without equilibrium approximations:
, is directly determined through the following networks of reactions without equilibrium approximations:
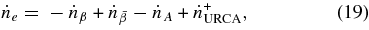
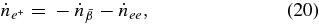
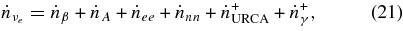
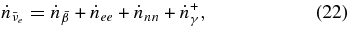

Here  , and
, and  are the net production rates of electrons, positrons, electron neutrinos, antielectron neutrinos, and heavy neutrinos. The heavy neutrino, νx, indicates the flavor of a heavy neutrino, νx = νμ, ντ. The changing rates,
are the net production rates of electrons, positrons, electron neutrinos, antielectron neutrinos, and heavy neutrinos. The heavy neutrino, νx, indicates the flavor of a heavy neutrino, νx = νμ, ντ. The changing rates, 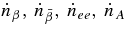 , and
, and  , are the net production rates of neutrinos by the following reactions; the β-process, e + p ⇌ νe + n, the positron capture on a neutron,
, are the net production rates of neutrinos by the following reactions; the β-process, e + p ⇌ νe + n, the positron capture on a neutron, 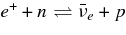 , the electron pair annihilation,
, the electron pair annihilation, 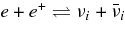 , where νi and
, where νi and 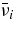 mean the flavors of the neutrinos and their antineutrinos, i.e., νi = νe, νμ, ντ and
mean the flavors of the neutrinos and their antineutrinos, i.e., νi = νe, νμ, ντ and  =
= 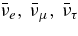 , the electron capture on a nucleus, e + A ⇌ νe + A', and the nucleon–nucleon bremsstrahlung,
, the electron capture on a nucleus, e + A ⇌ νe + A', and the nucleon–nucleon bremsstrahlung, 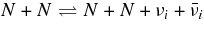 . The plus sign at the upper suffix denotes the production rates of neutrinos without inverse reactions of neutrinos, i.e.,
. The plus sign at the upper suffix denotes the production rates of neutrinos without inverse reactions of neutrinos, i.e., 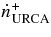 and
and 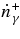 are the production rates by the URCA process, N + N → n + p + e + νe, and by the plasma decay,
are the production rates by the URCA process, N + N → n + p + e + νe, and by the plasma decay, 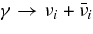 . The references and the numerical values of above reaction rates are summarized in Tables 1 and 5 (Appendix A).
. The references and the numerical values of above reaction rates are summarized in Tables 1 and 5 (Appendix A).
The reactions of leptons are evaluated in the simplified disk with the thickness H(r) in which the matter is assumed to be homogeneously distributed in the vertical direction. In the stationary accretion disk, the time variations of lepton, 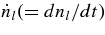 , are calculated in the shell comoving with the accreting flow such as
, are calculated in the shell comoving with the accreting flow such as 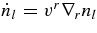 . The changing rates of leptons in the unit number of baryon for each reaction of neutrinos,
. The changing rates of leptons in the unit number of baryon for each reaction of neutrinos,  , are expressed in Table 5 (Appendix A). When the accreting matter moves along the distance,
, are expressed in Table 5 (Appendix A). When the accreting matter moves along the distance, 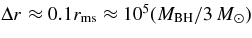 (cm) with the accreting velocity, vaccrt ≈ 10−3c ≈ 107 (cm s−1), where
(cm) with the accreting velocity, vaccrt ≈ 10−3c ≈ 107 (cm s−1), where 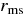 is the radius of a marginally stable orbit, the crossing time is Δt = Δr/vaccrt ≈ 10 (ms). In this time, the reactions of leptons are not always reach to the thermodynamic equilibrium. We expressively integrate the changing rate of leptons in time.
is the radius of a marginally stable orbit, the crossing time is Δt = Δr/vaccrt ≈ 10 (ms). In this time, the reactions of leptons are not always reach to the thermodynamic equilibrium. We expressively integrate the changing rate of leptons in time.
The change of the neutrino density is also brought about by the leakage of neutrinos from the disk. The transfer of neutrinos in a plane-parallel disk is solved in Appendix B. The number flux density of each neutrino, νi, at the surface of the disk, 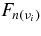 , is expressed with the production rate of the neutrino,
, is expressed with the production rate of the neutrino, 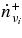 , the absorbing optical depth,
, the absorbing optical depth, 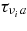 , the scattering optical depth,
, the scattering optical depth, 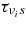 , and the total optical depth,
, and the total optical depth, 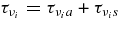 , as
, as
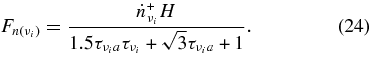
The absorbing opacity, 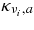 , and scattering opacities,
, and scattering opacities, 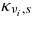 , of each flavor of neutrinos, νi, are described as
, of each flavor of neutrinos, νi, are described as
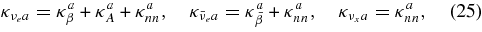
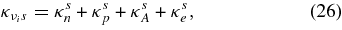
where 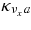 is the absorbing opacity of the heavy neutrino, νx = νμ, ντ;
is the absorbing opacity of the heavy neutrino, νx = νμ, ντ; 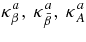 , and κann are the absorbing opacities by the inverse β-process, antielectron neutrino capture on a proton, electron neutrino capture on a nucleus, and by the inverse nucleon–nucleon bremsstrahlung. The opacities, κsn, κsp, κsA, and κse, indicate the scattering opacities of a neutrino, νi, with neutrons, protons, nuclei, and electrons. The explicit expressions of these opacities are represented in Table 3 (Appendix A).
, and κann are the absorbing opacities by the inverse β-process, antielectron neutrino capture on a proton, electron neutrino capture on a nucleus, and by the inverse nucleon–nucleon bremsstrahlung. The opacities, κsn, κsp, κsA, and κse, indicate the scattering opacities of a neutrino, νi, with neutrons, protons, nuclei, and electrons. The explicit expressions of these opacities are represented in Table 3 (Appendix A).
Table 3. Opacity
| No. | Neutrino Reaction | Opacity | Reference |
|---|---|---|---|
| 1 | νe + n → e + p | ![$\kappa ^a_\beta = \eta _{np}\frac{\int d^3p f_{\nu _e}(\varepsilon) \sigma _{\nu _e, n}^a(\varepsilon)[1-f_{e}(\varepsilon _{\nu _e}+Q)]}{\int d^3p f_{\nu _e}(\varepsilon)}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn78.gif) |
Burrows (2001) |
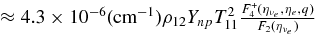 |
|||
| 2 | 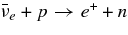 |
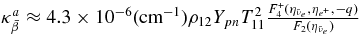 |
Burrows (2001) |
| 3 | 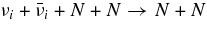 |
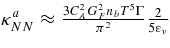 |
Raffelt (2001) |
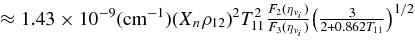 |
|||
| 4 | νe + A → e + A' |  |
|
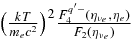 |
Bruenn (1985) | ||
| ≈1.2 × 10−6(cm−1)ρ12YAT211fA(η) | |||
| 5 | νi + N → νi + N | 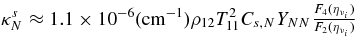 |
Burrows (2001) |
| 6 | νi + e → νi + e | 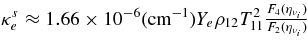 |
Burrows (2001) |
| 7 | νi + A → νi + A | 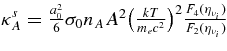 |
Bruenn (1985) |
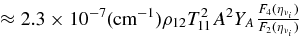 |
Notes. The absorption opacity, κa, and scattering opacity, κs, are expressed with unit cm−1. Fk(η) is the kth Fermi integral, Fk(η) ≡ ∫∞0xk(1 + exp(x − η))−1dx. The complex integrals, 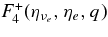 and
and 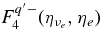 , are shown in Table 6. The doubly indexed quantity, Ynp, is the number fraction defined as Ynp = ηnp/nb, and Ypn is Ypn = exp(ηp − ηn)Ynp, where ηnp is the dynamic structure factor for neutrino–nucleon interaction,
, are shown in Table 6. The doubly indexed quantity, Ynp, is the number fraction defined as Ynp = ηnp/nb, and Ypn is Ypn = exp(ηp − ηn)Ynp, where ηnp is the dynamic structure factor for neutrino–nucleon interaction, ![$ \eta _{np} = \int \frac{2d^3p}{(2\pi)^3}f_n(\varepsilon)[1-f_p(\varepsilon)]=\frac{n_p-n_n}{\exp {(\eta _p -\eta _n)} -1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn93.gif) . YNN is
. YNN is 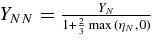 , and Cs,N is Cs,N = 1 if N = n and Cs,N = 0.827 if N = p. The factor, G2F, is the Fermi constant. Γ is the spin relaxation rate. A is the mean mass number of heavy nuclei. nA is the number density of heavy nuclei, and YA is the fraction, YA = nA/nb. Xn is the mass fraction of neutrons. fA(η) is
, and Cs,N is Cs,N = 1 if N = n and Cs,N = 0.827 if N = p. The factor, G2F, is the Fermi constant. Γ is the spin relaxation rate. A is the mean mass number of heavy nuclei. nA is the number density of heavy nuclei, and YA is the fraction, YA = nA/nb. Xn is the mass fraction of neutrons. fA(η) is 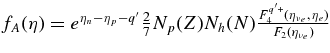 , where
, where 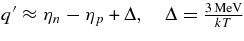 . Np(Z) and Nh(N) are Np(Z) = {0 for Z < 20; Z − 20 for 20 < Z < 28; 8 for Z>28} and Nh(N) = {6 for N < 34; 40 − N for 34 < N < 40; 0 for N>40}. The density ρ12 and temperature T11 are normalized values by 1012 (g cm−3) and 1011 K.
. Np(Z) and Nh(N) are Np(Z) = {0 for Z < 20; Z − 20 for 20 < Z < 28; 8 for Z>28} and Nh(N) = {6 for N < 34; 40 − N for 34 < N < 40; 0 for N>40}. The density ρ12 and temperature T11 are normalized values by 1012 (g cm−3) and 1011 K.
Download table as: ASCIITypeset image
Thus, the fraction change of each flavor of neutrinos, 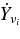 , and those of electrons and positrons,
, and those of electrons and positrons, 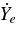 , are expressed by
, are expressed by
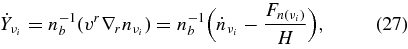

The emissivity of each flavor of neutrinos is described as
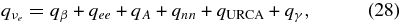
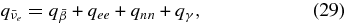
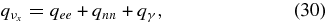
where  , and qγ are emissivities by the β-process, the positron capture on neutrons, the electron pair annihilation, the electron capture on nuclei, the nucleon–nucleon bremsstrahlung, the URCA process, and by the plasma decay. These explicit emissivities are expressed in Table 4 (Appendix A). The energy flux density of each flavor of neutrinos at the surface of the disk,
, and qγ are emissivities by the β-process, the positron capture on neutrons, the electron pair annihilation, the electron capture on nuclei, the nucleon–nucleon bremsstrahlung, the URCA process, and by the plasma decay. These explicit emissivities are expressed in Table 4 (Appendix A). The energy flux density of each flavor of neutrinos at the surface of the disk, 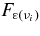 , is then given by
, is then given by
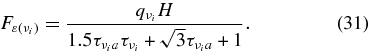
Table 4. Emissivity
| No. | Neutrino Reaction | Emission Rate | References |
|---|---|---|---|
| 1 | e + p → νe + n | 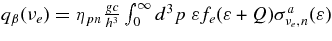 |
Burrows (2001) |
![$[1-f_{\nu _e}(\varepsilon)]$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn102.gif) |
|||
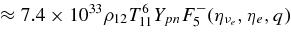 |
|||
| 2 | 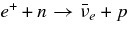 |
 |
Burrows (2001) |
| 3 | 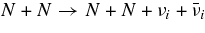 |
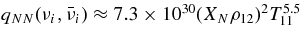 |
Burrows (2001) |
| 4 | e + A → νe + A' | 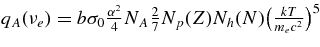 |
Bruenn (1985) |
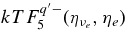 |
|||
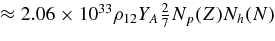 |
|||
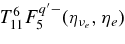 |
|||
| 5 | n + n → n + p + e + νe | 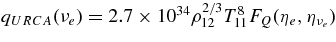 |
Shapiro & Teukolsky (1983) |
| 6 |  |
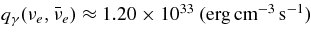 |
Ruffert et al. (1996) |
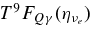 |
|||
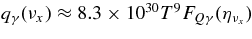 |
Ruffert et al. (1996) | ||
| 7 | 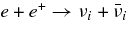 |
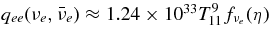 |
Thompson et al. (2000) |
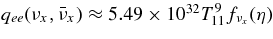 |
Thompson et al. (2000) |
Notes. The emission rates, q, are expressed with unit (erg cm−3 s−1). The complex integrals, 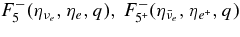 , and
, and 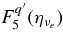 , are shown in Table 6, where q is q = Q/kT. FQ and
, are shown in Table 6, where q is q = Q/kT. FQ and  for i = e, x, are
for i = e, x, are  , and
, and 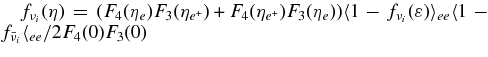 .
. 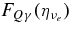 is
is 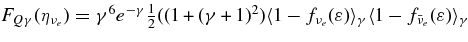 , where γ and γ0 are
, where γ and γ0 are 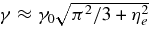 and γ0 = hΩ0/(2πmec2) = 5.565 × 10−2. The mean blocking factors
and γ0 = hΩ0/(2πmec2) = 5.565 × 10−2. The mean blocking factors 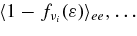 are described in Table 6.
are described in Table 6.
Download table as: ASCIITypeset image
Table 5. Fraction Change
| No. | Neutrino Reaction | Fraction Change |
|---|---|---|
| 1 | νe + n ⇌ e + p | 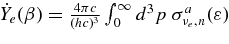 |
![$ [ Y_{np} f_{\nu _e}(\varepsilon) [1-f_{e}(\varepsilon +Q)] - Y_{pn} f_{e}(\varepsilon +Q) [1-f_{\nu _e}(\varepsilon)]]$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn130.gif) |
||
![$\approx 9.0\times 10^2\;({\rm s}^{-1}) T_{11}[Y_{np}F_4^+(\eta _{\nu _e},\eta _e,q)-Y_{pn}F_4^-(\eta _{\nu _e},\eta _e,q)]$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn131.gif) |
||
| 2 | νe + A ⇌ e + A' | 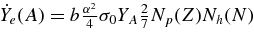 |
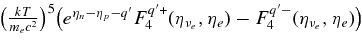 |
||
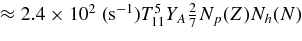 |
||
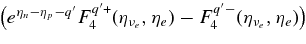 |
||
| 3 | n + n → n + p + e + νe | 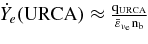 |
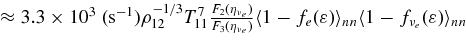 |
||
| 4 | 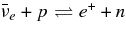 |
![$\dot{Y}_{e^+}(\bar{\nu }_e p) \approx 9.0\times 10^2\;({\rm s}^{-1}) T_{11}[Y_{pn}F_4^+(\eta _{\bar{\nu }_e},\eta _{e^+},-q)-Y_{np}F_4^-(\eta _{{\bar{\nu }} _e},\eta _{e^+},-q)]$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn139.gif) |
| 5 | 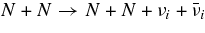 |
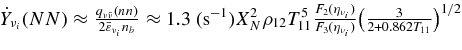 |
| 6 | 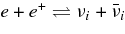 |
 |
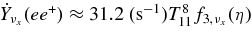 |
||
| 7 | 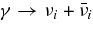 |
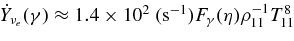 |
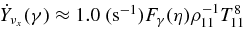 |
Notes. The parameter b is 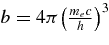 . The complex integrals,
. The complex integrals, 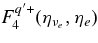 and
and 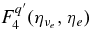 , are shown in Table 6.
, are shown in Table 6. 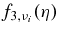 and
and 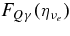 are
are 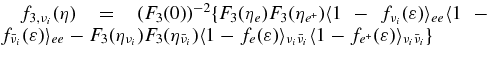 and
and 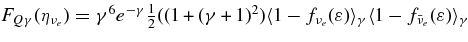 . The mean blocking factors
. The mean blocking factors 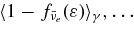 are described in Table 6. XN is the mass fraction of nucleons.
are described in Table 6. XN is the mass fraction of nucleons.
Download table as: ASCIITypeset image
Here, the spectra of leptons are assumed to be Fermi–Dirac distributions with the local gas temperature, T. When the density, nl, and temperature, T, are given, the chemical potential of the lepton, μl, is numerically determined through the Fermi integral,
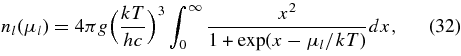
where g is the spin degeneracy.
3. RELATIVISTIC ACCRETION DISK
The ejection rate of neutrinos from the massive accretion disk depends significantly upon the temperature, T, and density, ρ, of the accreting matter. It is important precisely to determine the heat balance of the disk. In order to evaluate the proper heating rate by viscosity in the rotating spacetime, we introduce a set of local observers who rotate with the Keplerian, circular orbits (orbiting frame; Yokosawa & Inui 2005). The local energy conservation is rewritten in the orbiting frame. To avoid the infinite density at the inner boundary of the standard accretion disk proposed by Novikov & Thorne (1973), we resolve the transport equation of the angular momentum with the different boundary condition from the case of Novikov & Thorne (1973). The scale height of the disk and the heating rate by viscosity depend on the pressure and internal energy density of accreting matter with degenerate electrons and heavy nuclei. We shall represent here the stationary massive accretion disk unified in the rotating spacetime.
We introduce the Kerr spacetime and choose units with G = c = 1. The metric of the spacetime in terms of the Boyer–Lindquist time, t, and any arbitrary spatial coordinates, xj, has the form
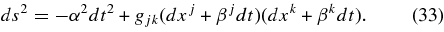
The metric coefficients, α, βj, and gjk, are the lapse, shift, and three-metric functions. These functions are given by
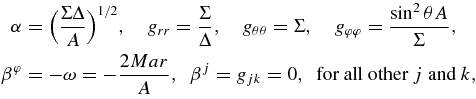
where M is the mass of a black hole and the functions, Δ, Σ, A, are defined by
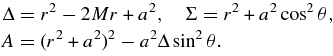
We introduce a set of local observers who rotate with the Keplerian, circular orbits (Yokosawa & Inui 2005). Each observer carries an orthogonal tetrad. For the Keplerian orbiting observer with a coordinate angular velocity of Ω, its world line is r = constant, θ = constant, φ = Ωt + constant. The observer in the locally non-rotating frame (LNRF; Bardeen et al. 1972) who rotates with the angular velocity, ω, measures the linear velocity of a particle moving in a Keplerian orbit as 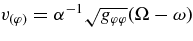 . Its Lorentz factor is γ = (1 − v2(φ))−1/2. We adopt the Keplerian orbiting, observer's frame ("orbiting frame") with the set of its basis vectors:
. Its Lorentz factor is γ = (1 − v2(φ))−1/2. We adopt the Keplerian orbiting, observer's frame ("orbiting frame") with the set of its basis vectors:
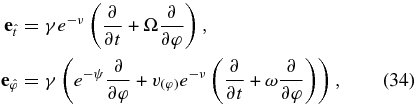
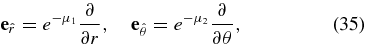
where  are defined by
are defined by  , respectively.
, respectively.
The corresponding orthogonal basis of one-forms is
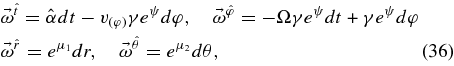
where 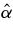 is defined by
is defined by 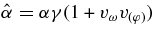 .
.
The shear stress in the Boyer–Lindquist coordinate is defined by
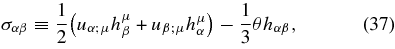
where θ is the expansion, θ = uαα, and hμν is the projection tensor, hμν = gμν + uμuν. The shear stress in the orbiting frame is expressed by
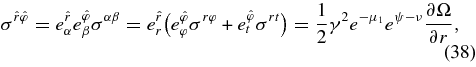
where  is the Boyer–Lindquist components of the basis of one-forms (Equation (36)),
is the Boyer–Lindquist components of the basis of one-forms (Equation (36)), 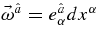 . The shear stress,
. The shear stress, 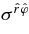 , in the orbiting frame is finite at the inner boundary of the accretion disk, r = rg, for a = 1 even though the radial difference in the orbiting frame is infinitesimal,
, in the orbiting frame is finite at the inner boundary of the accretion disk, r = rg, for a = 1 even though the radial difference in the orbiting frame is infinitesimal, 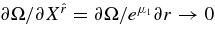 for r → rg, where rg is the gravitational radius of a black hole. It is also finite at the critical radius, r ≈ 2rg, where the differential rotation of the accreting matter measured in the LNRF (Bardeen et al. 1972) or by the zero angular momentum observers (ZAMOS; Thorne et al. 1986) is nothing, ∂(Ω − ω)/∂r = 0 at r ≈ 2rg, The shear stress,
for r → rg, where rg is the gravitational radius of a black hole. It is also finite at the critical radius, r ≈ 2rg, where the differential rotation of the accreting matter measured in the LNRF (Bardeen et al. 1972) or by the zero angular momentum observers (ZAMOS; Thorne et al. 1986) is nothing, ∂(Ω − ω)/∂r = 0 at r ≈ 2rg, The shear stress,  , is consistent with that given by Novikov & Thorne (1973).
, is consistent with that given by Novikov & Thorne (1973).
The production rate of the viscous heat in the orbiting frame is assumed as

where 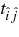 is the stress tensor. In the "α-model" of the viscosity, the stress tensor is expressed by
is the stress tensor. In the "α-model" of the viscosity, the stress tensor is expressed by 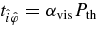 , where Pth is the thermal pressure and αvis is a parameter with αvis = 0.1 − 0.01.
, where Pth is the thermal pressure and αvis is a parameter with αvis = 0.1 − 0.01.
The energy–momentum tensor of the viscous fluid with the heat flux is described in the orbiting frame as (Misner et al. 1973; Novikov & Thorne 1973; Yokosawa 1995)
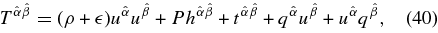
where ρ,  , and P are the rest-mass density, internal energy density, and the total pressure, and
, and P are the rest-mass density, internal energy density, and the total pressure, and  is the heat flux carried by neutrinos and photons. By using the covariant derivative,
is the heat flux carried by neutrinos and photons. By using the covariant derivative,  , the local energy conservation,
, the local energy conservation,  , is represented as
, is represented as
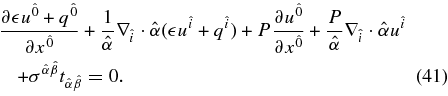
The mass conservation, 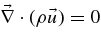 , is written as
, is written as
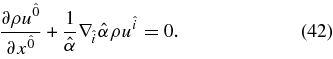
The conservation of angular momentum is clearly expressed in the frame fixed at the distant stars (Thorne et al. 1986). The Euler equation in the φ-direction is expressed in the Boyer–Lindquist coordinate as 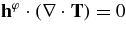 , where hφ is the projection vector in the φ-direction, hφ = hφβ. It is explicitly described as
, where hφ is the projection vector in the φ-direction, hφ = hφβ. It is explicitly described as
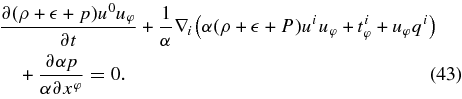
We are interesting in the gross properties of the disk. For simplicity, we consider the steady disk with an axially symmetry. As in the standard theory of the thin accretion disk (Novikov & Thorne 1973), we consider the height-averaged quantities. Putting the integrated stress as  and introducing the flux density at the surface of the disk,
and introducing the flux density at the surface of the disk,  , and the enthalpy, h = P +
, and the enthalpy, h = P +  , the energy equation is expressed by
, the energy equation is expressed by
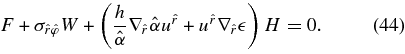
The flux density F is evaluated with the total flux density of neutrinos, 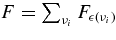 , where νi means each flavor of neutrinos,
, where νi means each flavor of neutrinos,  . The third term in Equation (44) is the heating by the convection, and the fourth term is the variation of the internal energy due to the movement of the matter along the flow. Since the completely degenerated matter cannot be cooled by the convection, the enthalpy in Equation (44) is changed by the thermal component of the enthalpy, h → hth = Pth +
. The third term in Equation (44) is the heating by the convection, and the fourth term is the variation of the internal energy due to the movement of the matter along the flow. Since the completely degenerated matter cannot be cooled by the convection, the enthalpy in Equation (44) is changed by the thermal component of the enthalpy, h → hth = Pth +  th.
th.
From Equation (43), the conservation of angular momentum is expressed by
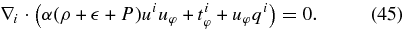
The angular momentum is transported by the viscous stress tiφ and by the neutrino flowing qi. Introducing the total mass flux,  , we described the transport equation of the angular momentum as
, we described the transport equation of the angular momentum as
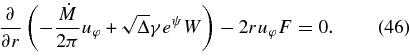
It has the solution:

where Π is the function with the value of unity at the great distance from the hole:

The term, fg, is due to the neutrino flowing. The functions, f and g, are
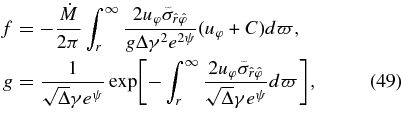
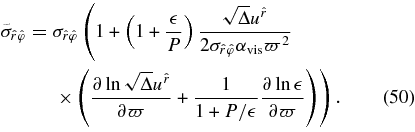
Here C is an integral constant. Novikov & Thorne (1973) adopted it as  since they assumed no viscous stress can act at
since they assumed no viscous stress can act at 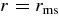 . The numerical simulations of the accretion disk with viscosity show that the accreting matter continuously flows into a black hole through the boundary radius
. The numerical simulations of the accretion disk with viscosity show that the accreting matter continuously flows into a black hole through the boundary radius 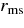 (Yokosawa 1995; De Villiers & Hawley 2003; De Villiers et al. 2003, 2005; Hirose et al. 2004; Krolik et al. 2005). We set the constant, C, such as the accreting matter continuously flows through the radius,
(Yokosawa 1995; De Villiers & Hawley 2003; De Villiers et al. 2003, 2005; Hirose et al. 2004; Krolik et al. 2005). We set the constant, C, such as the accreting matter continuously flows through the radius, 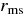 :
:
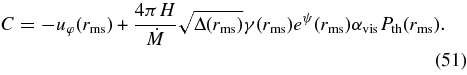
The energy equation (Equation (44)) and the transport equation of the angular momentum (Equation (47)) determine the stationary, thermally equilibrium structure of the accretion disk.
The thickness of the disk, H, in a dynamically equilibrium state is evaluated as follows. The equation of motion of the fluid, hkiTjk;j = 0, for the steady, axially symmetric, and circularly rotating fluid can be expressed in the total differential form:
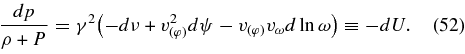
The equipressure surfaces are given by the equation U = constant. The quantity U = U(p) is equal in the Newtonian limit to the total potential (gravitational plus centrifugal potential) expressed in the units of c2 (Abramowicz et al. 1978). In the neighborhood of the equatorial plane, the potential, U, is expanded with z/r(≪1):

where Ω20 is

The function, Φ(r), becomes unity far away from a hole. Its explicit expression of Φ(r) is shown in Appendix C. The thickness of the disk, H, is approximately given by the scale height:
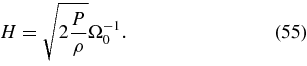
The total pressure, P, and the total internal energy density,  , of the accreting matter are given by
, of the accreting matter are given by
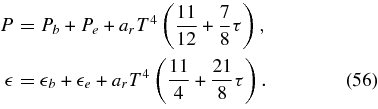
The third terms on the right-hand sides of both the expressions represent the contributions of the radiation and neutrinos in thermally equilibrium with relativistic electron positron pairs, where ar is the radiation constant and τ is the neutrino opacity, 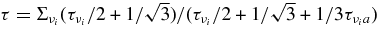 (Popham & Narayan 1995). The baryonic matter consists of free nucleons, α-particles, and heavy nuclei. Its pressure, Pb, is given by the EOS for the given density, ρ, temperature, T, and the fraction of electrons, Ye; Pb = Pb(ρ, T, Ye) (Lattimer & Swesty 1991). The values of Pb are almost the same as nbkT over the phase plane, 1011(g cm-3) < ρ < 1013 (g cm−3), 1010(K) < T < 1011(K), and 0.1 < Ye < 0.5. Thus, the thermal component of the internal energy of baryonic matter,
(Popham & Narayan 1995). The baryonic matter consists of free nucleons, α-particles, and heavy nuclei. Its pressure, Pb, is given by the EOS for the given density, ρ, temperature, T, and the fraction of electrons, Ye; Pb = Pb(ρ, T, Ye) (Lattimer & Swesty 1991). The values of Pb are almost the same as nbkT over the phase plane, 1011(g cm-3) < ρ < 1013 (g cm−3), 1010(K) < T < 1011(K), and 0.1 < Ye < 0.5. Thus, the thermal component of the internal energy of baryonic matter, 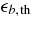 , is set as
, is set as 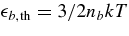 . The pressure and the internal energy of electrons, Pe and
. The pressure and the internal energy of electrons, Pe and  e, are expressed approximately by (Lattimer & Swesty 1991)
e, are expressed approximately by (Lattimer & Swesty 1991)
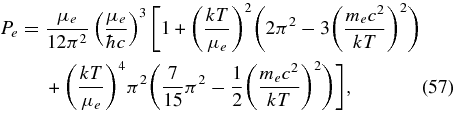
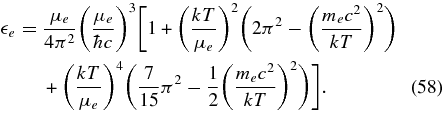
The first terms in both the square brackets provide the pressure and internal energy corresponding to the completely degenerated state. The second and third terms depend on the temperature. In the state of massive accretion disks, the degeneracy factor of electrons has the value in the range 2 < ηe < 15 (see Figure 6). We adopt the above expressions without the first term as thermal pressure and thermal internal energy of electrons, 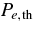 and
and  .
.
4. RESULTS
We have solved the stationary equations of the accreting flow, Equations (44) and (47), and the fraction changes of leptons (Equation (28)) measured in the orbiting frame, 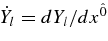 , from the outer boundary,
, from the outer boundary, 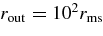 , to the inner boundary,
, to the inner boundary, 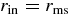 . At the outer boundary, we adopt the components of neutrinos,
. At the outer boundary, we adopt the components of neutrinos, 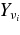 , in quasi-equilibrium abundance in the given (ρ, T, Ye); the quasi-equilibrium abundance,
, in quasi-equilibrium abundance in the given (ρ, T, Ye); the quasi-equilibrium abundance, 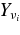 , satisfies the conditions,
, satisfies the conditions, 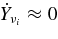 for each neutrino νi. The fraction of electrons, Ye, which satisfies the stationary conditions, Equations (44) and (47), is taken to be the most large value within Ye ⩽ 0.5. The accreting velocity,
for each neutrino νi. The fraction of electrons, Ye, which satisfies the stationary conditions, Equations (44) and (47), is taken to be the most large value within Ye ⩽ 0.5. The accreting velocity, 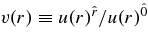 , is derived from the mass conservation,
, is derived from the mass conservation, 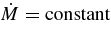 , for the given density, ρ(r), and height, H(r). The time interval of the accreting fluid moving the distance,
, for the given density, ρ(r), and height, H(r). The time interval of the accreting fluid moving the distance, 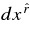 , is taken as
, is taken as 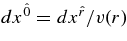 . We introduce the normalized values of the radius,
. We introduce the normalized values of the radius,  , accretion rate,
, accretion rate, 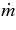 , and the mass of a black hole, m, defined as
, and the mass of a black hole, m, defined as 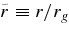 ,
, 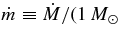 s−1), and m ≡ MBH/M☉. The accretion rate,
s−1), and m ≡ MBH/M☉. The accretion rate, 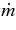 , and the angular momentum of a black hole, a, are selected as
, and the angular momentum of a black hole, a, are selected as 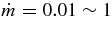 and a = 0 ∼ 1. The typical parameters for the model of GRBs are such as
and a = 0 ∼ 1. The typical parameters for the model of GRBs are such as 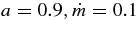 , and m = 3 (MacFadyen & Woosley 1999). The viscous parameter is set to be αvis = 0.05.
, and m = 3 (MacFadyen & Woosley 1999). The viscous parameter is set to be αvis = 0.05.
4.1. Effects of Heavy Nuclei on the Massively Accreting Matter
The loci of accreting matter in the ρ–T plane for 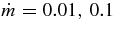 , and 1 are shown in Figure 1. The contours of the difference in chemical potentials between a neutron and a proton, μn − μp, provided by EOS are overplotted. The profile of the contour changes distinctly at the phase boundary between the matter with heavy nuclei and the uniform gas of evaporated free nucleons and α-particles without heavy nuclei (Lamb et al. 1981; Lattimer & Swesty 1991). The loci of the accreting matter are put in the domain with coexistence of heavy nuclei. The massive accretion disks contain non-ignorable abundance of heavy nuclei.
, and 1 are shown in Figure 1. The contours of the difference in chemical potentials between a neutron and a proton, μn − μp, provided by EOS are overplotted. The profile of the contour changes distinctly at the phase boundary between the matter with heavy nuclei and the uniform gas of evaporated free nucleons and α-particles without heavy nuclei (Lamb et al. 1981; Lattimer & Swesty 1991). The loci of the accreting matter are put in the domain with coexistence of heavy nuclei. The massive accretion disks contain non-ignorable abundance of heavy nuclei.
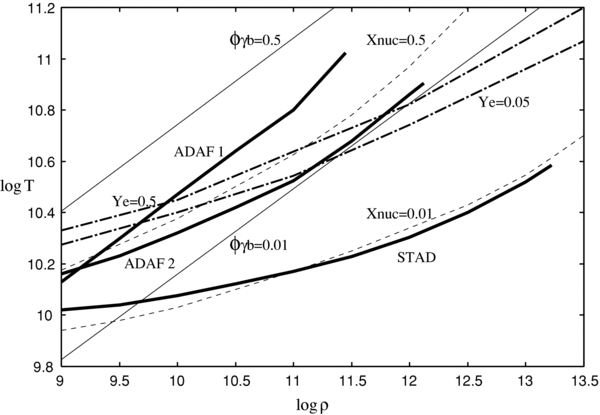
The locus of the typical accretion disk (STAD) with 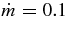 and those of ADAFs, ADAF1 for
and those of ADAFs, ADAF1 for 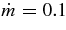 (Di Matteo et al. 2002) and ADAF2 for
(Di Matteo et al. 2002) and ADAF2 for 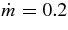 (Chen & Belobororodov 2007), are also plotted on the ρ–T plane in Figure 2. The matter of STAD takes the state with relatively low temperature and high density. The quasi-radially falling matter in ADAF is heated up by the strong compression due to rapid deceleration, and the heated thermal energy is confined within the neutrino-opaque disk. The geometrically thin disk (STAD) produces high dense and neutrino-transparent matter in which the frequent neutrino reactions are enhanced.
(Chen & Belobororodov 2007), are also plotted on the ρ–T plane in Figure 2. The matter of STAD takes the state with relatively low temperature and high density. The quasi-radially falling matter in ADAF is heated up by the strong compression due to rapid deceleration, and the heated thermal energy is confined within the neutrino-opaque disk. The geometrically thin disk (STAD) produces high dense and neutrino-transparent matter in which the frequent neutrino reactions are enhanced.
Figure 2. Loci of the accreting matter on the ρ (g cm−3)–T (K) plane. The loci of the advection dominating accretion flows with neutrino loss, ADAF1 given by Di Matteo et al. (2002) and ADAF2 given by Chen & Belobororodov (2007), and the locus of STAD obtained in this paper are plotted by thick lines. Here, the accretion rate and the mass of a black hole in both loci are selected to be 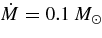 s−1 for ADAF1 and STAD,
s−1 for ADAF1 and STAD, 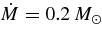 s−1 for ADAF2, and MBH = 3 M☉ for all. The constant photon-to-baryon ratios, ϕγb = 0.5, 0.01, are depicted by thin lines. The constant mass fractions of free nucleons given by Qian & Woosley (1996), Xnuc = 0.5, 0.01, are plotted by dashed lines. The phase boundaries between the matter with heavy nuclei and the uniform gas of evaporated free nucleons and α-particles without heavy nuclei, where μn,A − μp,A = μn,G − μp,G, for the cases, Ye = 0.5, 0.05 (Lamb et al. 1981) are described by the dot-dashed lines.
s−1 for ADAF2, and MBH = 3 M☉ for all. The constant photon-to-baryon ratios, ϕγb = 0.5, 0.01, are depicted by thin lines. The constant mass fractions of free nucleons given by Qian & Woosley (1996), Xnuc = 0.5, 0.01, are plotted by dashed lines. The phase boundaries between the matter with heavy nuclei and the uniform gas of evaporated free nucleons and α-particles without heavy nuclei, where μn,A − μp,A = μn,G − μp,G, for the cases, Ye = 0.5, 0.05 (Lamb et al. 1981) are described by the dot-dashed lines.
Download figure:
Standard image High-resolution imageThe mass fraction of free nucleons produced by the photodisintegration process, Xnuc = T9/811ρ−3/412exp(−0.61/T11), is presented by Qian & Woosley (1996). In the previous work (Di Matteo et al. 2002), the free nucleons have been evaluated by Xnuc. The locus of the typical accretion disk (STAD) is almost resemble with that of the mass fraction, Xnuc = 10−2. If the mass fraction of free nucleons is evaluated by Xnuc, the fraction of free neutrons becomes very small. The amount of free neutrons in the massive accretion disk can be provided by the evaporation process from the heavy nuclei in high dense matter (Lattimer & Swesty 1991). The phase boundaries between the matter with heavy nuclei and the uniform gas of evaporated free nucleons without heavy nuclei in the states, Ye = 0.5, 0.05 (Lamb et al. 1981), are also plotted in Figure 2. The matters in ADAFs pass over the boundaries. If the neutrino reactions in the domain of heavy nuclei are introduced and if the detailed balances are relaxed in ADAFs, other loci of ADAFs may be represented in the ρ–T plane.
The free nucleons could also be produced by the photodisintegration if there were enough photons to disintegrate the nuclei (Burbidge et al. 1957; Meyer et al. 1992). The photon-to-baryon ratio ϕγb is expressed as
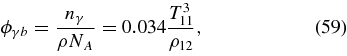
where NA is Avog dro's number. The constant lines of the ratio for ϕγb = 0.5 and 0.01 are shown in Figure 2. All the loci of the accreting flows are put at the domain of insufficient photons with ϕγb < 0.1.
dro's number. The constant lines of the ratio for ϕγb = 0.5 and 0.01 are shown in Figure 2. All the loci of the accreting flows are put at the domain of insufficient photons with ϕγb < 0.1.
4.2. Degeneracy of Accreting Particles
The profiles of degeneracy factors of electrons ηe(=μe/kT) and neutron–proton difference ηnp(=(μn − μp)/kT) are shown in Figure 3. The degeneracy of electrons ηe in the massive accretion is strong, ηe ≈ 5 ∼ 10, though the electrons are not always in the completely degenerated state. In the previous works in ADAF (Chen & Belobororodov 2007; Kawanaka & Mineshige 2007), it is mild, ηe ≈ 1 ∼ 3. The degeneracy factors of neutron–proton difference are also strong, ηnp ≈ 6 ∼ 12, in the typical case of the accretion with  and a = 0.9. Since the number ratio of the free neutron to the free proton is proportional to the degeneracy factor, nn/np ≈ exp(ηnp), the increase of the degeneracy ηnp from 6 at the outer region to 12 at the inner side of the disk is corresponding to the variation of number ratio such as nn/np ≈ 4 × 102 → 105. The degeneracy factor of
and a = 0.9. Since the number ratio of the free neutron to the free proton is proportional to the degeneracy factor, nn/np ≈ exp(ηnp), the increase of the degeneracy ηnp from 6 at the outer region to 12 at the inner side of the disk is corresponding to the variation of number ratio such as nn/np ≈ 4 × 102 → 105. The degeneracy factor of 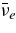 reaches to
reaches to 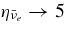 at the inner boundary of the disk. The increases in ηnp and ηe are caused by the contraction of accreting matter with relatively low temperature. The rapid decreases of ηnp and ηe at the inner side of the disk are brought about by the rapid decrease of Ye.
at the inner boundary of the disk. The increases in ηnp and ηe are caused by the contraction of accreting matter with relatively low temperature. The rapid decreases of ηnp and ηe at the inner side of the disk are brought about by the rapid decrease of Ye.
Figure 3. Profiles of the degeneracy factors. The degeneracy factors, ηnp = (μn − μp)/kT, are shown by solid lines and those of the electron, ηe = μe/kT, are plotted by dashed lines. The profiles denoted by the accretion rates,  , 0.05, 0.02 (M☉ s−1), are presented for the cases with a = 0.9, and those by
, 0.05, 0.02 (M☉ s−1), are presented for the cases with a = 0.9, and those by 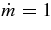 (M☉ s−1) are given by the accretion with a = 0. The mass of a black hole is fixed as MBH = 3 M☉.
(M☉ s−1) are given by the accretion with a = 0. The mass of a black hole is fixed as MBH = 3 M☉.
Download figure:
Standard image High-resolution imageThe thermal equilibrium approximation in the β-process is not always in high degree of accuracy for the massively accreting matter. While the degeneracy factors of ηnp and ηe change in similar profiles along the flow, the thermal equilibrium approximation, ηe = ηnp + Q/kT, is not satisfied, but the degeneracy factor ηnp becomes superior to ηe at the inner side of the accretion disk.
4.3. Composition of Accreting Matter
The profiles of the composition of accreting matter are shown in Figures 4 and 5. The case of the low accretion rates, 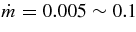 for a = 0.9, is shown in Figure 4. On the other hand, Figure 5 shows the profiles for massive accretion rates,
for a = 0.9, is shown in Figure 4. On the other hand, Figure 5 shows the profiles for massive accretion rates, 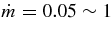 for a = 0. The profiles of compositions of baryons (free neutrons and free protons) and of leptons (electrons, positrons, electron neutrinos, antielectron neutrinos, and heavy neutrinos) have been represented at first. The characteristic property of the accreting matter is the remarkable discrepancy in the fractions between free neutrons and protons. The fraction of free neutrons becomes dominant at the inner side of the disk, Yn = 0.7 ∼ 0.8, while that of free protons decreases to an extremely minor composition, Yp = 10−4 ∼ 10−5. When the gas consists of free neutrons, protons, and electrons, the minimum ratio of np/nn in the thermally equilibrium state is np/nn = 2.6 × 10−3 at ρ = 7.8 × 1011 (g cm−3) (Shapiro & Teukolsky 1983). In the high dense matter with heavy nuclei, the free protons become extremely infinitesimal.
for a = 0. The profiles of compositions of baryons (free neutrons and free protons) and of leptons (electrons, positrons, electron neutrinos, antielectron neutrinos, and heavy neutrinos) have been represented at first. The characteristic property of the accreting matter is the remarkable discrepancy in the fractions between free neutrons and protons. The fraction of free neutrons becomes dominant at the inner side of the disk, Yn = 0.7 ∼ 0.8, while that of free protons decreases to an extremely minor composition, Yp = 10−4 ∼ 10−5. When the gas consists of free neutrons, protons, and electrons, the minimum ratio of np/nn in the thermally equilibrium state is np/nn = 2.6 × 10−3 at ρ = 7.8 × 1011 (g cm−3) (Shapiro & Teukolsky 1983). In the high dense matter with heavy nuclei, the free protons become extremely infinitesimal.
Figure 4. Profiles of the composition of the accreting matter. The left side shows the profiles of the electron fraction, Ye, positron fraction, 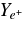 , free neutron fraction, Yn, and of the free proton fraction, Yp. The right side shows the fraction of each type of neutrinos, electron neutrinos,
, free neutron fraction, Yn, and of the free proton fraction, Yp. The right side shows the fraction of each type of neutrinos, electron neutrinos, 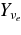 , antielectron neutrinos,
, antielectron neutrinos, 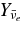 , and that of heavy neutrinos,
, and that of heavy neutrinos,  . The mass of a black hole and the rotating parameter are set as MBH = 3 M☉ and a = 0.9. The numbers of the labels, 1, 2, 3, 4, 5, denote the cases for accretion rates,
. The mass of a black hole and the rotating parameter are set as MBH = 3 M☉ and a = 0.9. The numbers of the labels, 1, 2, 3, 4, 5, denote the cases for accretion rates, 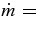 0.005, 0.01, 0.02, 0.05, 0.1 (M☉ s−1).
0.005, 0.01, 0.02, 0.05, 0.1 (M☉ s−1).
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 4, but for the massive accreting case. The numbers of the labels, 1, 2, 3, 4, 5 denote the cases for accretion rates, 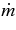 = 0.05, 0.2, 0.5, 0.7, 1 (M☉ s−1). The rotating parameter of a black hole is a = 0.
= 0.05, 0.2, 0.5, 0.7, 1 (M☉ s−1). The rotating parameter of a black hole is a = 0.
Download figure:
Standard image High-resolution imageThe high density and the sufficient time in the reactions of leptons change the fraction of electrons, Ye, which gradually decreases along the accreting flow and reaches to Ye = 0.01 at the inner boundary, 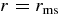 . The fraction of electron neutrinos
. The fraction of electron neutrinos 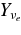 rapidly decreases along the flow, while the fraction of antielectron neutrinos
rapidly decreases along the flow, while the fraction of antielectron neutrinos 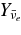 gradually increases to be
gradually increases to be 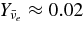 at the inner disk. The fraction of heavy neutrinos
at the inner disk. The fraction of heavy neutrinos 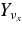 increases in proportional to the density of accreting matter. The heavy neutrinos are produced mainly by the reactions,
increases in proportional to the density of accreting matter. The heavy neutrinos are produced mainly by the reactions, 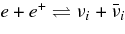 and,
and, 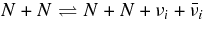 . In massively accreting cases,
. In massively accreting cases, 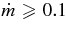 for a = 0.9, the heavy neutrinos are not negligibly rare and their fraction exceeds the electron neutrinos at the inner side of the disk,
for a = 0.9, the heavy neutrinos are not negligibly rare and their fraction exceeds the electron neutrinos at the inner side of the disk, 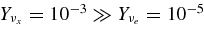 .
.
When the accretion rate 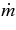 increases, the fraction of protons decreases,
increases, the fraction of protons decreases, 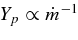 , though the fraction of neutrons at the inner side of the disk remains almost constant in the wide range of accretion rate; Yn ≈ 0.7 ∼ 0.8 for
, though the fraction of neutrons at the inner side of the disk remains almost constant in the wide range of accretion rate; Yn ≈ 0.7 ∼ 0.8 for 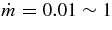 . Similarly, the fractions of electron neutrinos
. Similarly, the fractions of electron neutrinos 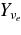 and that of positrons
and that of positrons 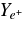 are inversely proportional to
are inversely proportional to  , while the fraction of antielectron neutrinos
, while the fraction of antielectron neutrinos 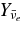 remains almost constant,
remains almost constant, 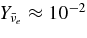 . On the contrary, the fraction of heavy neutrinos increases as
. On the contrary, the fraction of heavy neutrinos increases as 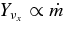 . At the inner side of the disk with
. At the inner side of the disk with 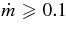 , the heavy neutrinos become a non-ignorable component in the network of the lepton reactions.
, the heavy neutrinos become a non-ignorable component in the network of the lepton reactions.
4.4. Flow Structures of Accretion Disks
The flow profiles, density ρ(r), temperature T(r), accreting velocity v(r), and thickness H(r), are plotted in Figures 6 and 7. Figure 6 shows the distinctive flow structures for the variation of accretion rate, 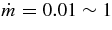 , where the central mass is fixed as m = 3. Figure 7 shows the flow profiles depending on the mass scale of a black hole, m = 1 ∼ 10. The remarkable feature of the accreting flow is the profile of the temperature. The temperature becomes nearly constant along the flow, T ≈ 3 × 1010 K, and little changes for the wide range of accretion rate,
, where the central mass is fixed as m = 3. Figure 7 shows the flow profiles depending on the mass scale of a black hole, m = 1 ∼ 10. The remarkable feature of the accreting flow is the profile of the temperature. The temperature becomes nearly constant along the flow, T ≈ 3 × 1010 K, and little changes for the wide range of accretion rate, 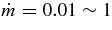 . This characteristic property is caused the optically thin disk for the antielectron neutrinos. The main emissivity of
. This characteristic property is caused the optically thin disk for the antielectron neutrinos. The main emissivity of 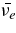 is given by the reaction of positron capture on neutrons whose emissivity is sensitive to temperature,
is given by the reaction of positron capture on neutrons whose emissivity is sensitive to temperature, 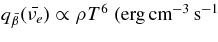 ) (Burrows 2001). The optically thin antielectron neutrinos adjust the temperature balanced between heating and cooling of the disk. The height of the geometrically thin disk is also little changed,
) (Burrows 2001). The optically thin antielectron neutrinos adjust the temperature balanced between heating and cooling of the disk. The height of the geometrically thin disk is also little changed, 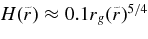 , for
, for 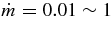 , The accreting velocity, v, is uniform along the flow, v ≈ 10−3c. The typical dynamic time of the accretion disk is Δt ≈ 102rg/v ≈ 10 (s). The density of accreting matter reaches to a very high value at the inner disk, ρ ≈ 1013 ∼ 1014 (g cm−3), for
, The accreting velocity, v, is uniform along the flow, v ≈ 10−3c. The typical dynamic time of the accretion disk is Δt ≈ 102rg/v ≈ 10 (s). The density of accreting matter reaches to a very high value at the inner disk, ρ ≈ 1013 ∼ 1014 (g cm−3), for 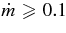 .
.
Figure 6. Flow profiles of the density, ρ (g cm−3), temperature, T (K), drift velocity, v (cm s−1), and of the thickness, H (cm). The mass of a black hole is fixed to be MBH = 3 M☉, and the angular momentum parameters are selected such as a = 0, 0.9, 1. The flow profiles with a = 0.9 and 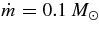 s−1 are shown by filled lines, and those with a = 1 and
s−1 are shown by filled lines, and those with a = 1 and 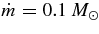 s−1 are plotted by dashed lines. The profiles with a = 0.9 and
s−1 are plotted by dashed lines. The profiles with a = 0.9 and 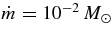 s−1 are depicted by dotted lines. The profiles with a = 0 and
s−1 are depicted by dotted lines. The profiles with a = 0 and 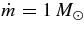 s−1 are shown by dot-dashed lines. The radius, r, is normalized by the gravitational radius, rg.
s−1 are shown by dot-dashed lines. The radius, r, is normalized by the gravitational radius, rg.
Download figure:
Standard image High-resolution imageFigure 7. Same as Figure 6, but for the dependences of the mass scale of a black hole. The numbers denote the masses of a black hole such as MBH = 1, 2, 3, 5, 10 (M☉). The accretion rate and the specific angular momentum of a black hole are fixed as 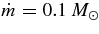 s−1 and a = 0.
s−1 and a = 0.
Download figure:
Standard image High-resolution imageFigure 6 shows that the central density at r = rin depends on the mass of a black hole as ρ(rin) ∝ m−2 and the thermally equilibrium temperature is inversely proportional to the mass, T(rin) ∝ m−1/3. The profiles of density 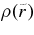 and temperature
and temperature 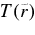 are expressed approximately as
are expressed approximately as 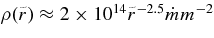 g cm−3 and
g cm−3 and 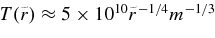 K. When the mass of a black hole increases owing to the accreting flow, the central density and temperature around a black hole rapidly change with time. The emission rate of antielectron neutrinos is then
K. When the mass of a black hole increases owing to the accreting flow, the central density and temperature around a black hole rapidly change with time. The emission rate of antielectron neutrinos is then  (Burrows 2001). Even if the emitting region of neutrinos is
(Burrows 2001). Even if the emitting region of neutrinos is 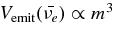 , the neutrino flux will decrease with time after the birth of a black hole when the accretion rate is nearly constant.
, the neutrino flux will decrease with time after the birth of a black hole when the accretion rate is nearly constant.
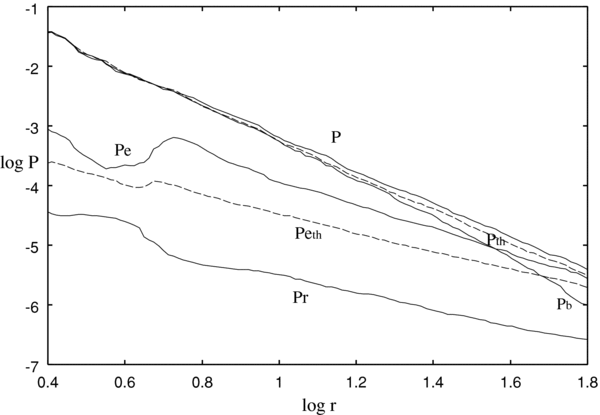
The vertical structure of a massive accretion disk is supported mainly by baryons. The compositions of the pressure, Pb, Pe, and Pr, and of the thermal pressure, Pth and  , for the typical case of the accretion are shown in Figure 8. Even though the electrons are degenerated, the inner disk is little supported by the electrons but mainly supported by baryons (free neutrons), Pb ≫ Pe. The accreting free neutrons are continuously heated by viscosity and thus its pressure Pb becomes superior to Pe at the region r < 30rg. The electron pressure Pe itself decreases at the inner region of the disk where the electron fraction Ye rapidly decreases. The thermal part of the electron pressure
, for the typical case of the accretion are shown in Figure 8. Even though the electrons are degenerated, the inner disk is little supported by the electrons but mainly supported by baryons (free neutrons), Pb ≫ Pe. The accreting free neutrons are continuously heated by viscosity and thus its pressure Pb becomes superior to Pe at the region r < 30rg. The electron pressure Pe itself decreases at the inner region of the disk where the electron fraction Ye rapidly decreases. The thermal part of the electron pressure  is comparable with the degenerated part of Pe. The contribution of the radiation pressure Pr to the total pressure P is negligibly small, Pr ≪ P.
is comparable with the degenerated part of Pe. The contribution of the radiation pressure Pr to the total pressure P is negligibly small, Pr ≪ P.
Figure 8. Component of the pressure. The total pressure, P, pressure of electrons, Pe, that of baryonic matter, Pb, and the radiation pressure, Pr, are shown. The total thermal pressure, Pth, and the thermal pressure of electrons, 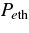 , are plotted. The parameters of the typical accretion with
, are plotted. The parameters of the typical accretion with  s−1, MBH = 3 M☉ and a = 0.9 are selected. The unit of the pressure, P, is (MeV fm−3).
s−1, MBH = 3 M☉ and a = 0.9 are selected. The unit of the pressure, P, is (MeV fm−3).
Download figure:
Standard image High-resolution image4.5. Emissivities and Opacities of Neutrinos
The emissivities of each flavor of neutrinos 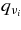 and that ejected by each type of neutrino reactions for the typical accretion disk are shown in Figure 9. The energy flux density of each flavor of neutrinos for the typical accretion disk
and that ejected by each type of neutrino reactions for the typical accretion disk are shown in Figure 9. The energy flux density of each flavor of neutrinos for the typical accretion disk  is shown in Figure 10. The antielectron neutrino acts as the most efficient source of emissivity. The emissivity of antielectron neutrinos
is shown in Figure 10. The antielectron neutrino acts as the most efficient source of emissivity. The emissivity of antielectron neutrinos 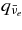 is provided mainly by the positron capture on a neutron,
is provided mainly by the positron capture on a neutron, 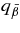 ;
;  . At the inner side of the disk, the emissivity by heavy neutrinos
. At the inner side of the disk, the emissivity by heavy neutrinos 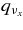 becomes efficient, which is provided by the reactions of the nucleon–nucleon bremsstrahlung qnn and the electron pair process qee. The emissivity of electron neutrinos
becomes efficient, which is provided by the reactions of the nucleon–nucleon bremsstrahlung qnn and the electron pair process qee. The emissivity of electron neutrinos 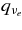 is 1 order of magnitude less than
is 1 order of magnitude less than  since the proton fraction Yp is infinitesimal. At the outer side of the disk,
since the proton fraction Yp is infinitesimal. At the outer side of the disk, 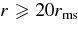 , the pair production, qee;
, the pair production, qee;  , and the nuclei reaction, qA, e + A → νe + A', sufficiently contribute to the total emissivity. At the inner side of the disk, the URCA process
, and the nuclei reaction, qA, e + A → νe + A', sufficiently contribute to the total emissivity. At the inner side of the disk, the URCA process  is efficient. The emissivity of neutrinos rapidly increases along the flow. The total emissivity is expressed as
is efficient. The emissivity of neutrinos rapidly increases along the flow. The total emissivity is expressed as  erg cm−3 s−1.
erg cm−3 s−1.
Figure 9. Profiles of the total emissivity of neutrinos, q, and those of the emissivities of antielectron neutrinos, 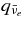 , electron neutrinos,
, electron neutrinos, 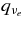 , and of heavy neutrinos,
, and of heavy neutrinos, 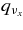 , are plotted in the typical case of the accretion with MBH = 3 M☉, a = 0.9, and
, are plotted in the typical case of the accretion with MBH = 3 M☉, a = 0.9, and 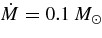 s−1. The emissivities by the β-process, qβ, positron capture on a neutron,
s−1. The emissivities by the β-process, qβ, positron capture on a neutron,  , e− e+ pair annihilation, qee, the URCA process,
, e− e+ pair annihilation, qee, the URCA process, 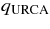 , nucleon–nucleon bremsstrahlung, qnn, plasma process, qplasma, and nucleus reaction, qA, are also depicted. The unit of emissivity, q, is (erg cm−3 s−1).
, nucleon–nucleon bremsstrahlung, qnn, plasma process, qplasma, and nucleus reaction, qA, are also depicted. The unit of emissivity, q, is (erg cm−3 s−1).
Download figure:
Standard image High-resolution imageFigure 10. Profiles of the total flux density of neutrinos, F, and of the flux density of antielectron neutrinos, 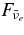 , heavy neutrinos,
, heavy neutrinos, 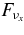 , and of electron neutrinos,
, and of electron neutrinos, 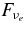 , are plotted. The unit of flux density, F, is (erg cm−2 s−1). The parameters of accretion are the same as in Figure 9.
, are plotted. The unit of flux density, F, is (erg cm−2 s−1). The parameters of accretion are the same as in Figure 9.
Download figure:
Standard image High-resolution imageThe flux density of antielectron neutrinos at the surface of the disk 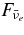 rapidly increases along the accreting flow while that of electron neutrinos
rapidly increases along the accreting flow while that of electron neutrinos 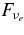 maintains almost the constant value. The ratio of the flux density of
maintains almost the constant value. The ratio of the flux density of 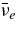 to that of νe becomes large to be
to that of νe becomes large to be 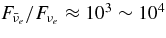 at the inner side of the disk, since the electron neutrinos are almost absorbed by dense neutrons. The flux density of νx rapidly increases in the vicinity of the inner boundary and reaches to be comparable with
at the inner side of the disk, since the electron neutrinos are almost absorbed by dense neutrons. The flux density of νx rapidly increases in the vicinity of the inner boundary and reaches to be comparable with 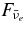 . The total flux density is expressed as
. The total flux density is expressed as 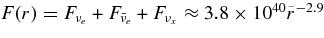 erg cm−2 s−1 in the typical case of the accretion.
erg cm−2 s−1 in the typical case of the accretion.
The opacity and the optical depth of each flavor of neutrinos are shown in Figure 11. The absorbing opacity of electron neutrinos κa(νe) is by far larger than those of other flavors of neutrino, 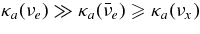 . The electron neutrino νe is absorbed mainly by dense free neutrons through the reaction νe + n → e + p, while the antielectron neutrino
. The electron neutrino νe is absorbed mainly by dense free neutrons through the reaction νe + n → e + p, while the antielectron neutrino  is little absorbed by rare free protons,
is little absorbed by rare free protons, 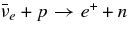 . The scattering opacities of
. The scattering opacities of 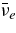 and νe are in the same order except near the inside boundary where the chemical potential of
and νe are in the same order except near the inside boundary where the chemical potential of 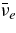 is some larger than that of νe,
is some larger than that of νe, 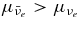 , which brings about the larger scattering opacity of
, which brings about the larger scattering opacity of 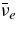 ;
; 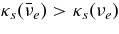 . The total optical depths of
. The total optical depths of 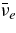 and νe are in the same order of magnitude and become very large at the inner disk,
and νe are in the same order of magnitude and become very large at the inner disk, 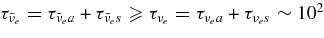 . However, there is a remarkable difference in the effective optical depth among them,
. However, there is a remarkable difference in the effective optical depth among them, 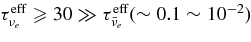 , where the effective optical depth is defined as
, where the effective optical depth is defined as 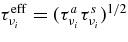 . Most of νe are absorbed in the disk and their energy is deposited in the accreting matter. On the other hand, the antielectron neutrinos
. Most of νe are absorbed in the disk and their energy is deposited in the accreting matter. On the other hand, the antielectron neutrinos  carry out the thermal energy of the accreting matter from the disk. The effective optical depth of νe is approximately described as
carry out the thermal energy of the accreting matter from the disk. The effective optical depth of νe is approximately described as 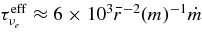 . It becomes over unity at the radius,
. It becomes over unity at the radius, 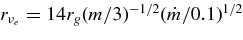 , where the neutrino sphere (disk) of νe is formed. The neutrino sphere (disk) of
, where the neutrino sphere (disk) of νe is formed. The neutrino sphere (disk) of 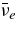 or νx is not formed for
or νx is not formed for 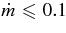 . The total optical depths of
. The total optical depths of 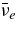 and νe become over unity,
and νe become over unity, 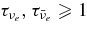 , at the radius,
, at the radius, 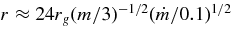 .
.
Figure 11. Profiles of absorption opacity, κa(νi), scattering opacity, κs(νi), effective optical depth, τeff(νi), and of total optical depth, 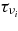 , for νi = νe, νe, νx, are plotted. The opacity by the neutrino–nucleus reaction is labeled by κaA. The unit of opacity, κ, is (cm−1). The parameters of accretion are the same as in Figure 9.
, for νi = νe, νe, νx, are plotted. The opacity by the neutrino–nucleus reaction is labeled by κaA. The unit of opacity, κ, is (cm−1). The parameters of accretion are the same as in Figure 9.
Download figure:
Standard image High-resolution image4.6. Luminosity and Mean Energy of Neutrinos
The total luminosities Lν and the mean energies 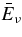 of neutrinos measured at infinity are plotted in Figure 11, where the mass of a black hole m, angular momentum a, and the accretion rate
of neutrinos measured at infinity are plotted in Figure 11, where the mass of a black hole m, angular momentum a, and the accretion rate  are changed over the range such as m = 1 ∼ 10, a = 0 ∼ 1, and
are changed over the range such as m = 1 ∼ 10, a = 0 ∼ 1, and 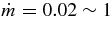 . We evaluate the luminosity Lν and mean energy
. We evaluate the luminosity Lν and mean energy 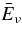 as follows. The luminosity measured at the infinity is expressed in the Boyer–Lindquist coordinate as
as follows. The luminosity measured at the infinity is expressed in the Boyer–Lindquist coordinate as
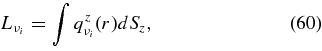
where 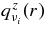 is the z-component of the flux density vector at the radius r, where the z-direction is the vertical one to the disk, and dSz is the z-component of the surface element vector, dSz = α−12πrdr (Thorne et al. 1986). The component,
is the z-component of the flux density vector at the radius r, where the z-direction is the vertical one to the disk, and dSz is the z-component of the surface element vector, dSz = α−12πrdr (Thorne et al. 1986). The component, 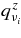 , is connected to the local surface density in the orbiting frame
, is connected to the local surface density in the orbiting frame 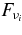 such as
such as

where 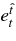 is the t-component of the orbiting basis
is the t-component of the orbiting basis 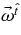 expressed in Equation (36),
expressed in Equation (36), 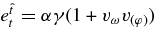 . Thus the luminosity observed at the infinity is expressed by
. Thus the luminosity observed at the infinity is expressed by
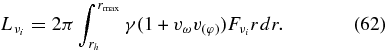
The mean energy of neutrinos emitted from the accretion disk  for each type of neutrino is defined as follows. When the neutrinos are thermally equilibrium in the accreting matter, the local mean energy of neutrino
for each type of neutrino is defined as follows. When the neutrinos are thermally equilibrium in the accreting matter, the local mean energy of neutrino  is expressed by the matter temperature T(r) and the degeneracy factor of neutrino
is expressed by the matter temperature T(r) and the degeneracy factor of neutrino 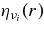 :
:
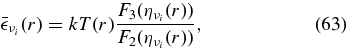
where  is the kth Fermi integral, Fk(η) ≡ ∫∞0(1 + exp(x − η))−1xkdx, for k = 2, 3. The number of neutrinos emitted from the shell (ring) over the width of radius, r ∼ r + dr, per unit time is given by
is the kth Fermi integral, Fk(η) ≡ ∫∞0(1 + exp(x − η))−1xkdx, for k = 2, 3. The number of neutrinos emitted from the shell (ring) over the width of radius, r ∼ r + dr, per unit time is given by
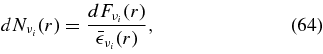
where 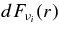 is the energy flux of neutrinos from the shell (ring) with the width dr. The total number of neutrinos for each type of neutrinos is described as
is the energy flux of neutrinos from the shell (ring) with the width dr. The total number of neutrinos for each type of neutrinos is described as 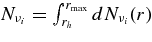 . Thus, the mean energy of neutrinos for each type of neutrinos is defined as
. Thus, the mean energy of neutrinos for each type of neutrinos is defined as 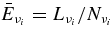 .
.
The total luminosity for all types of neutrinos is 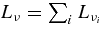 . The mean energy in all types of neutrinos is simply defined by
. The mean energy in all types of neutrinos is simply defined by 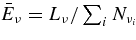 . We set the quantities of neutrinos within
. We set the quantities of neutrinos within  to be the same as the values at the boundary,
to be the same as the values at the boundary,  . The maximum radius of the integral is taken to be rmax = 102rg.
. The maximum radius of the integral is taken to be rmax = 102rg.
The diagram of the luminosity of neutrinos, Lν, versus the mean energy, 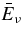 , in Figure 12 shows the characteristic properties as follows. (1) The luminosity Lν and the mean energy
, in Figure 12 shows the characteristic properties as follows. (1) The luminosity Lν and the mean energy 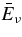 are proportional to the specific angular momentum of a black hole, Lν ∝ a and
are proportional to the specific angular momentum of a black hole, Lν ∝ a and 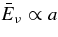 . When m = 3 and
. When m = 3 and 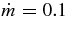 , the ratio of the luminosity for a = 1 to that for a = 0 is Lν(a = 1)/Lν(a = 0) ≈ 3.5, and the ratio of mean energy is
, the ratio of the luminosity for a = 1 to that for a = 0 is Lν(a = 1)/Lν(a = 0) ≈ 3.5, and the ratio of mean energy is  . (2) The luminosity is proportional to the accretion rate,
. (2) The luminosity is proportional to the accretion rate, 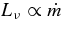 , but it is almost independent of the mass scale of a black hole, Lν ≈ constant, for m = 1 ∼ 10. (3) The mean energy of neutrinos
, but it is almost independent of the mass scale of a black hole, Lν ≈ constant, for m = 1 ∼ 10. (3) The mean energy of neutrinos  is proportional to the accretion rate while it is inversely proportional to the mass of a black hole,
is proportional to the accretion rate while it is inversely proportional to the mass of a black hole, 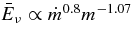 . If the luminosity of each flavor of neutrinos
. If the luminosity of each flavor of neutrinos  and its mean energy
and its mean energy  are observed (Halzen & Hooper 2002; McDonald et al. 2004), the physical parameters of a central black hole will be made clear.
are observed (Halzen & Hooper 2002; McDonald et al. 2004), the physical parameters of a central black hole will be made clear.
Figure 12. Neutrino luminosity, L (erg s−1), vs. mean energy of an ejected neutrino, E (MeV), observed at infinity. The luminosity, L, and the mean energy, E, for the variation of specific angular momentum of a black hole, a = 0 → 1, are depicted by the dot-dashed line labeled as m = 3[a = 0, 1], where the other parameters of the accretion are fixed to be MBH = 3 M☉ and  s−1. Those for MBH = 1, 2, 3, 4, 5, 6, 8, 10(M☉) are connected by the line labeled as a = 0.9[m = 10, 1], where the angular parameter of a black hole and the accretion rate are fixed as a = 0.9 and
s−1. Those for MBH = 1, 2, 3, 4, 5, 6, 8, 10(M☉) are connected by the line labeled as a = 0.9[m = 10, 1], where the angular parameter of a black hole and the accretion rate are fixed as a = 0.9 and 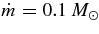 s−1. Those for
s−1. Those for 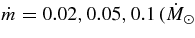 s−1) are labeled as a = 0.9 [dotm=0.02, 0.1], where the angular parameter and the mass of a black hole are fixed as a = 0.9 and MBH = 3 M☉. Those for a = 0, 0.7 are similarly shown.
s−1) are labeled as a = 0.9 [dotm=0.02, 0.1], where the angular parameter and the mass of a black hole are fixed as a = 0.9 and MBH = 3 M☉. Those for a = 0, 0.7 are similarly shown.
Download figure:
Standard image High-resolution imageThe typical accretion disk provides the luminosity, Lν ∼ 1052 erg s−1, and the mean energy,  MeV, which is several times larger than the thermal energy of a particle in the disk. This high mean energy
MeV, which is several times larger than the thermal energy of a particle in the disk. This high mean energy  is caused by the large degeneracy,
is caused by the large degeneracy,  , at the inner disk. The energy flux, Lν ∼ 1052 erg s−1, with the mean energy,
, at the inner disk. The energy flux, Lν ∼ 1052 erg s−1, with the mean energy, 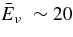 MeV, emitted from a disk could produce the outward flow in the vertical direction to the disk.
MeV, emitted from a disk could produce the outward flow in the vertical direction to the disk.
5. DISCUSSION
We have studied the massive accretion disk in a simplified model in which the disk is assumed to be stationary and its vertical structure is treated by the one-zone model with the thickness H. These simplifications might restrict the properties of the accretion disk. We first discuss the transient thermal stability of the disk.
5.1. Transient Thermal Instability
The scattering optical depth of antielectron neutrinos is 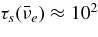 for the typical accretion disk. Then, the diffusion time of the neutrinos is tdiff ≈ τsH/c ≈ 10 (ms). One of the characteristic features of γ-ray emission is the short spike-like emissions with the duration time Δt ⩽ 10 ms. When the sufficiently rapid increase of heat δh is generated in the disk, the excess of heat is deposited within the disk in the duration of tdiff, which could drive the transient thermal instability of the accretion disk. We discuss the transient thermal stability by a perturbation analysis.
for the typical accretion disk. Then, the diffusion time of the neutrinos is tdiff ≈ τsH/c ≈ 10 (ms). One of the characteristic features of γ-ray emission is the short spike-like emissions with the duration time Δt ⩽ 10 ms. When the sufficiently rapid increase of heat δh is generated in the disk, the excess of heat is deposited within the disk in the duration of tdiff, which could drive the transient thermal instability of the accretion disk. We discuss the transient thermal stability by a perturbation analysis.
When the scattering optical depth is large, τs ≫ 1, and the absorption optical depth is negligible, τa ≪ 1, the neutrinos randomly walk in the disk. The time in which a neutrino is trapped in the disk is expressed as tdiff ≈ Nl/c ≈ (l/c)(H/l)2 ≈ (H/l)(H/c) ≈ τstcross, where N is the collision number of a neutrino in the disk, l is the mean free path, and tcross is the crossing time over the scale height H. The time required for a neutrino to escape from the disk is τs times larger than the crossing time over the scale height. We assume a perturbation δh in the disk. When τs ≪ 1, the change of the cooling rate in the unit column of the disk is then expressed as δQ− = δFν = δh/tcross = δ(qνH). When τs ≫ 1, we can express the perturbation of the cooling rate as δQ− = δh/tdiff = δ(qνH)/τs. Since the electron neutrinos νe are almost absorbed within the disk, we express its perturbed cooling rate as 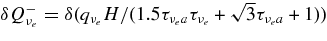 . The perturbed cooling rates by
. The perturbed cooling rates by 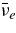 , νx, and νe for any optical depth can be represented as
, νx, and νe for any optical depth can be represented as
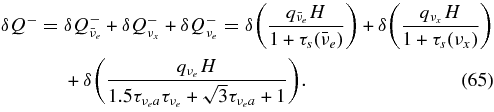
The change of heating rate is δQ+ = δQvis + δQadv where δQvis and δQadv are changes by viscous heating and by advection. We evaluate the thermal stability for the perturbation of temperature δT with the restriction of constant surface density Σ,
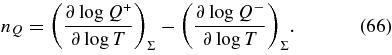
The value of the displacement, Q+(T + δT) or Q−(T + δT), for Σ = constant, is numerically calculated and then the value of differential, 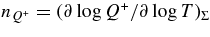 or
or 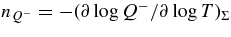 , is obtained.
, is obtained.
The result for the net index of the differential, 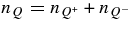 , is shown in Figure 13, where the parameters of the accretion disk are set as
, is shown in Figure 13, where the parameters of the accretion disk are set as 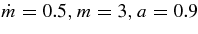 , and αvis = 0.1. The sign of nQ becomes positive when
, and αvis = 0.1. The sign of nQ becomes positive when 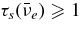 . The sign of
. The sign of  also becomes positive when
also becomes positive when  , since the opacity of
, since the opacity of  so rapidly increases for the increase of temperature,
so rapidly increases for the increase of temperature, 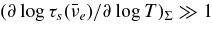 , that the differential of the cooling rate by temperature becomes negative,
, that the differential of the cooling rate by temperature becomes negative,  . For the region where the scattering optical depth of
. For the region where the scattering optical depth of 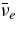 is larger than unity,
is larger than unity, 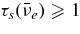 , the accretion disk becomes thermally unstable at least within the duration of the diffusion time tdiff.
, the accretion disk becomes thermally unstable at least within the duration of the diffusion time tdiff.
Figure 13. Change of net heating rate, nQ, due to the increase of temperature, δT. The index of the differential of the heating rate by the temperature, 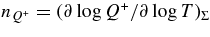 , and that of the cooling rate,
, and that of the cooling rate, 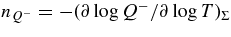 , are depicted by dashed lines. The scattering optical depth of antielectron neutrinos,
, are depicted by dashed lines. The scattering optical depth of antielectron neutrinos, 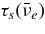 , is plotted by a dot-dashed line. When the net index,
, is plotted by a dot-dashed line. When the net index, 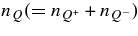 , is positive, the accretion disk becomes thermally unstable. The parameters of accretion are set as
, is positive, the accretion disk becomes thermally unstable. The parameters of accretion are set as 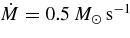 , MBH = 3 M☉, a = 0.9, and αvis = 0.1.
, MBH = 3 M☉, a = 0.9, and αvis = 0.1.
Download figure:
Standard image High-resolution imageWe next discuss on the dynamics of nucleons interacting with neutrinos. In the typical case of the accretion disk, the effective optical depth of electron neutrinos τeff(νe) exceeds unity at the radius, r ⩽ 10rg. The ratio of the flux density of νe to that of 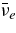 becomes infinitesimal,
becomes infinitesimal, 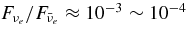 , which seriously restricts the efficiency of the annihilation of νe and
, which seriously restricts the efficiency of the annihilation of νe and 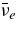 at the outer side of the disk. This results in the difficulty in the formation of a fireball by the pair annihilation between νe and
at the outer side of the disk. This results in the difficulty in the formation of a fireball by the pair annihilation between νe and 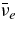 . However, the effective optical depths of
. However, the effective optical depths of 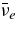 and νx within the radius r ⩽ 10rg are less than unity,
and νx within the radius r ⩽ 10rg are less than unity,  , and their scattering optical depths are greater than unity,
, and their scattering optical depths are greater than unity, 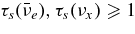 . The interactions of
. The interactions of 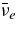 and νx with the nucleons might push the nucleon matter outward and could drive the convection or neutrino driving wind or jets. Since the mean energy of neutrinos exceeds the rest-mass energy of electrons,
and νx with the nucleons might push the nucleon matter outward and could drive the convection or neutrino driving wind or jets. Since the mean energy of neutrinos exceeds the rest-mass energy of electrons, 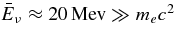 for the accretion with a ⩾ 0.9,
for the accretion with a ⩾ 0.9, 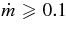 and m ⩽ 3, the collisions between neutrinos and electrons efficiently transfer the momentum and energy from neutrinos to electrons (Thompson et al. 2000). The intensive wind or jets from the disk might be produced. The one-dimensional flow driven by neutrinos will become fast in comparison with the radial flow in a supernova explosion.
and m ⩽ 3, the collisions between neutrinos and electrons efficiently transfer the momentum and energy from neutrinos to electrons (Thompson et al. 2000). The intensive wind or jets from the disk might be produced. The one-dimensional flow driven by neutrinos will become fast in comparison with the radial flow in a supernova explosion.
The intense flux of antielectron neutrinos is ejected from the disk but the electron neutrinos absorbed in the accreting matter fall into a black hole, which means that the lepton number decreases in the free world apart from the event horizon. In the case of the typical accretion disk with  , the ejection rate of neutrinos is
, the ejection rate of neutrinos is 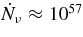 s−1. The baryon number of a star with the mass M = 1M☉ is Nb ≈ 1057. The lepton number which is 1 order of magnitude larger than the baryon number falling into a black hole decreases in an event of a GRB.
s−1. The baryon number of a star with the mass M = 1M☉ is Nb ≈ 1057. The lepton number which is 1 order of magnitude larger than the baryon number falling into a black hole decreases in an event of a GRB.
We have studied the stationary accretion disk with neutrino loss and evaluated the effects of neutrinos on the structure of the disk. The dynamics of the neutrino-driven wind, the dynamical behaviors at the inner disk, and the thermal instability of the massive accretion disk should be farther more precisely investigated by the non-stationary numerical methods of general relativistic hydrodynamics.
6. SUMMARY
We summarize the new results in this paper in comparison with previous works as follows.
- 1.Effects of heavy nuclei on the massively accreting matter. The heavy nuclei ignored in previous works play an important role in the massive accretion disk. In the high dense matter with ρ = 109 ∼ 1013 g cm−3, the heavy nuclei interact with ambient nucleons. The fraction of free protons interacting with heavy nuclei is extremely small, Yp = 10−4–10−5, while that in the free nucleons without heavy nuclei is Yp = Yn = Ye = 10−1–10−2 (Chen & Belobororodov 2007; Kawanaka & Mineshige 2007; Lee et al. 2005). This difference decides the opacity of neutrinos in the dense region of accreting matter. In previous works, the neutrinos become opaque at the inner disk, while
 in the heavy nuclei are transparent all over the disk. The huge neutrinos extract the thermal energy (liberated gravitational energy) in the disk and may play an important role in the formation of relativistic jets emitting γ-ray bursts. On the other hand, the neutrinos absorbed in the accreting matter fall into a black hole.
in the heavy nuclei are transparent all over the disk. The huge neutrinos extract the thermal energy (liberated gravitational energy) in the disk and may play an important role in the formation of relativistic jets emitting γ-ray bursts. On the other hand, the neutrinos absorbed in the accreting matter fall into a black hole. - 2.Accretion disk with Keplerian angular momentum. Previous works on the massive accreting matter with neutrino loss are based on ADAF (Popham et al. 1999; Chen & Belobororodov 2007; Kawanaka & Mineshige 2007). Since the formation of collimated jets requires pre-collapsed matter of a massive star with sufficient angular momentum, we have investigated the STAD with Keplerian angular momentum. The thermal history of accreting matter in ADAF is dissimilar to that in STAD. The strong compression by the rapid deceleration of ADAF at the middle region of the accretion disk largely heats up the accreting matter to be in the state of free nucleons. The gradual viscous heating and efficient cooling by antielectron neutrinos in STAD maintains the accreting matter at relatively low temperature, T ≈ 3 × 1010 K over a long range of accreting radius which produces very high dense matter, ρ ≈ 1012 ∼ 1013 g cm−3, around a central black hole.
- 3.Detailed balances in neutrino reactions. The reactions of leptons in the previous works of ADAF have been assumed to hold the detailed balances (Belorborodov 2003). These conditions of the detailed balances restrict the variations of ρ, T, and Ye along the flow. However, these simplified assumptions of the detailed balances are not adequate for the massive accretion with degenerated electrons. We have solved the lepton reactions by the direct methods without equilibrium conditions and shown the profiles of lepton fractions along the flow. The electron fraction becomes very small at the inner disk, Ye < 0.01.
- 4.Mean energy of ejected neutrinos. The mean energy of neutrinos ejected from the disk is large,
 MeV, in comparison with previous results,
MeV, in comparison with previous results,  MeV (Lee et al. 2005), because the neutrinos,
MeV (Lee et al. 2005), because the neutrinos,  , in STAD are generated in high dense matter with large degeneracy,
, in STAD are generated in high dense matter with large degeneracy,  T,
T,  . The production condition of "neutrino-driven wind" (Qian & Woosley 1996) is satisfied in the case of STAD while it is difficult for ADAF.
. The production condition of "neutrino-driven wind" (Qian & Woosley 1996) is satisfied in the case of STAD while it is difficult for ADAF. - 5.Transient thermal instability. We have investigated the transient thermal instability of the massive accretion disk cooled by
 , where the scattering optical depth is very large,
, where the scattering optical depth is very large,  . The accretion disk becomes thermally unstable at least within the duration of the diffusion time, tdiff ≈ 10 ms, which is the characteristic period of γ-ray emission for the short spike-like emissions.
. The accretion disk becomes thermally unstable at least within the duration of the diffusion time, tdiff ≈ 10 ms, which is the characteristic period of γ-ray emission for the short spike-like emissions.
We thank Professor T. Yoshida for helpful discussions and for very useful comments that improved the presentation of the paper.
APPENDIX A: REACTION RATES OF NEUTRINOS
The cross sections of neutrinos, opacities, emissivities, and reaction rates used in our model are listed in Tables 2–6. The numerical functions used in the reaction rates are listed in Table 6. Here the spectra of leptons are assumed to be Fermi–Dirac distributions with the local gas temperature T. The blocking in the lepton phase space is calculated by the approximate expressions given by Ruffert et al. (1996).
Table 6. Integrals and Blocking Factors
| No. | Integrals and Blocking Factors |
|---|---|
| 1 |  |
| 2 | 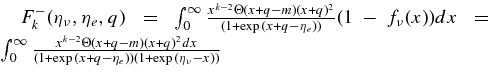 |
| 3 | 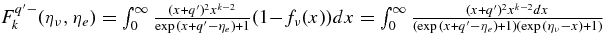 |
| 4 |  |
| 5 | ![$\langle 1-f_{e}(\varepsilon)\rangle _{nn} \approx \big\lbrace 1+\exp {\big[\eta _{e}-\frac{F_5(\eta _n)}{F_4(\eta _n)}\big]} \big\rbrace ^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn395.gif) |
| 6 | ![$\langle 1-f_{\nu }(\varepsilon)\rangle _{nn} \approx \big\lbrace 1+\exp {\big[\eta _{\nu }-\frac{F_5(\eta _n)}{F_4(\eta _n)}\big]} \big \rbrace ^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn396.gif) |
| 7 | ![$\langle 1-f_{\nu _i}(\varepsilon)\rangle _{ee} \approx \big\lbrace 1+\exp {\big[\eta _{\nu _i}-\frac{1}{2}\big (\frac{F_5(\eta _e)}{F_4(\eta _e) }+\frac{F_5(\eta _{e^+})}{F_4(\eta _{e^+})}\big) \big]} \big \rbrace ^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn397.gif) |
| 8 | ![$\langle 1-f_{e}(\varepsilon +q^{\prime })\rangle \approx \big \lbrace 1+\exp {\big [ \eta _e -\frac{F_5(\eta _{\nu _e})}{F_4(\eta _{\nu _e})} -q^{\prime }\big ]} \big \rbrace ^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn398.gif) |
| 9 | ![$\langle 1-f_{\nu _i}(\varepsilon)\rangle _\gamma \approx \big (1+\exp {\big [\eta _{\nu _i}-\big(1+\frac{1}{2} \frac{\gamma ^2}{1+\gamma }\big)\big ]}\big)^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn399.gif) |
| 10 | ![$\langle 1-f(\eta _{e^+})\rangle \approx \big\lbrace 1+\exp {[-(\bar{\varepsilon }^+ - \eta _{e^+})]} \big \rbrace ^{-1}$](https://content.cld.iop.org/journals/0004-637X/715/1/86/revision1/apj309667ieqn400.gif) , , 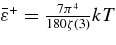 . . |
Notes. The quantity Θ(x) is the unit step function, Θ(x) = 0 if x < 0 and Θ(x) = 1 if x ⩾ 0. The quantity ζ(3) is the ζ(n) function with n = 3, ζ(3) = 1.202, and m is m = mec2/kT.
Download table as: ASCIITypeset image
APPENDIX B: TRANSFERS OF NEUTRINOS IN A PLANE-PARALLEL DISK
The accretion disk cooled by neutrinos is geometrically very thin. The calculating position is limited for r>1.885rg, where 1.885rg is the radius with null shear stress for a = 1. The radial velocity of the accreting flow in the orbiting frame is not relativistic. We neglect the relativistic effects on the transports of neutrinos. The analytic formulae of neutrino's transfers in the orbiting frame are derived by using the simplified treatment of the radiative transfer given by Popham & Narayan (1995). The  -coordinate is taken to be perpendicular to the equatorial plane. Introducing the two streams, with intensities I+, I− moving at an angle
-coordinate is taken to be perpendicular to the equatorial plane. Introducing the two streams, with intensities I+, I− moving at an angle 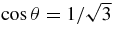 relative to
relative to  and
and  , defines the net flux density j and the total intensity
, defines the net flux density j and the total intensity 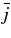 such as
such as 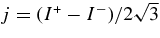 and
and 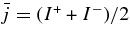 . The transfers of neutrinos are then described by the production rate of neutrinos
. The transfers of neutrinos are then described by the production rate of neutrinos  , absorption opacity κa, scattering opacity κs, and the total opacity κ = κa + κs as
, absorption opacity κa, scattering opacity κs, and the total opacity κ = κa + κs as
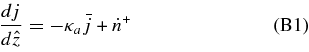

The boundary condition at the center of the disk is j = 0. To derive the simplest solution, let us assume that 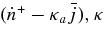 are independent of
are independent of  (Hubeny 1990). Equations (B1) and (B2) can be integrated to give
(Hubeny 1990). Equations (B1) and (B2) can be integrated to give
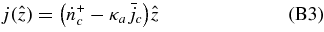
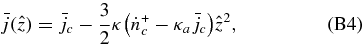
where 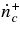 and
and 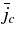 are the values of
are the values of 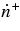 and
and 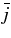 at the center of the disk,
at the center of the disk, 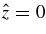 . The boundary condition at the surface of the disk is I− = 0, i.e.,
. The boundary condition at the surface of the disk is I− = 0, i.e., 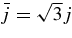 . Applying this boundary condition, we find
. Applying this boundary condition, we find
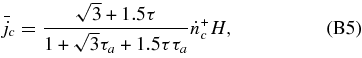
where τa is the absorbing optical depth, τa = κaH, and τ is the total optical depth, τ = κH. The escaping flux density of any sort of neutrino νi is then given by
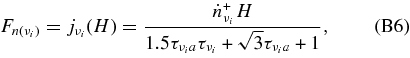
where  and
and  are the total optical depth and the absorbing optical depth of νi, and
are the total optical depth and the absorbing optical depth of νi, and  is the production rate of νi per unit volume.
is the production rate of νi per unit volume.
APPENDIX C: THE DYNAMICAL STRUCTURE OF THE DISK
The dynamically equilibrium structure of the disk is given by the Euler equation. The equation of motion of the fluid, hkiTjk;j = 0, for the steady, axially symmetric, and rotating ideal fluid can be expressed in the total differential form:
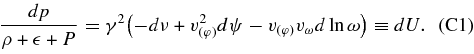
The equipressure surfaces are given by the equation, U=constant. In the Newtonian limit the quantity U = U(p) is equal to the total potential (gravitational plus centrifugal ones) expressed in the units of c2 (Abramowicz et al. 1978). We solve the disk structure in terms of cylindrical coordinates ϖ, z, and φ instead of radial coordinates which are combined through the relations
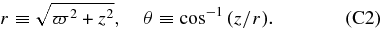
If no pressure force exerts in the ϖ-direction, Equation (C1) determines the velocity of the geodesic circular orbit, v(φ). Let us introduce the new variables,  defined by
defined by 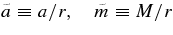 , s ≡ sin θ, c ≡ cos θ. The following functions are defined by
, s ≡ sin θ, c ≡ cos θ. The following functions are defined by
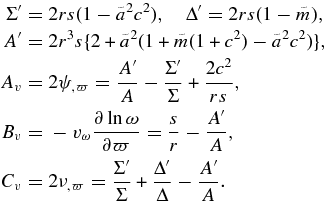
The circular velocity is then given by
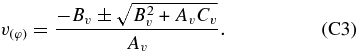
This velocity at the equatorial plane is expresses as
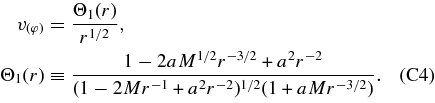
The vertical force is described by the gradient of the equipotential, ∇zU. The first order of the expansion of ∂U/∂z in z/r(≪1) gives the approximate expression such as